Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Системы массового обслуживания (СМО)
Содержание
- 1. Системы массового обслуживания (СМО)
- 2. Системы массового обслуживания (СМО) телефонные станции, ремонтные
- 3. Признаки СМОслучайный входящий поток требований, нуждающихся в обслуживании, дисциплина очереди, механизм (алгоритм), осуществляющий это обслуживание
- 4. Схема СМОПроцесс работы СМО представляет собой случайный
- 5. Предмет ТМОпостроение математических моделей, связывающих заданные условия
- 6. Показатели эффективности СМОсреднее число заявок, обслуживаемыхСМО в
- 7. Задачи ТМОрасчет показателей эффективности оптимизация функционирования СМО
- 8. Терминология ТМО (по Кендаллу)Для обозначения модели используют
- 9. Распределение вероятностей M - экспоненциальное распределение;D -
- 10. ПримерM| D| 2- экспоненциальное распределение времени
- 11. Классификация СМОпо условию ожидания СМО с отказами
- 12. Дисциплина обслуживания в порядке поступления – FIFO,
- 13. Потоки событий Последовательность однородных событий, следующих одно
- 14. Свойства потоков Поток событий называется регулярным, если
- 15. Стационарность Поток событий называется стационарным, если
- 16. БеспоследействиеПоток событий называется потоком без последействия, если
- 17. ОрдинарностьПоток событий называется ординарным, если
- 18. Простейший потокПоток событий, обладающий всеми тремя свойствами,
- 19. Пуассоновский поток Вероятность попадания на участок
- 20. Распределение времени между событиями в простейшем потоке
- 21. Промежуток времени Т
- 22. ОрдинарностьP0(Δt) - вероятность того, что на участке
- 23. Слайд 23
- 24. Уравнения КолмогороваСостояния системы с дискретными состояниями и
- 25. Уравнения КолмогороваВероятности состояний p1(t), p2(t), p3(t), p4(t).pi(t)
- 26. Уравнения КолмогороваПридадим t малое приращение Δt и
- 27. Уравнения Колмогорова В
- 28. Скачать презентанцию
Системы массового обслуживания (СМО) телефонные станции, ремонтные мастерские, билетные кассы, справочные бюро,производственные процессы,вычислительные процессы, технологические процессы,магазины, поликлиника, транспорт и т.п.
Слайды и текст этой презентации
Слайд 2Системы массового обслуживания (СМО)
телефонные станции,
ремонтные мастерские,
билетные кассы,
Слайд 3Признаки СМО
случайный входящий поток требований,
нуждающихся в обслуживании,
дисциплина
очереди,
механизм (алгоритм), осуществляющий
это обслуживание
Слайд 4Схема СМО
Процесс работы СМО представляет собой
случайный процесс с дискретными
состояниями и непрерывным временем
Состояние СМО меняется скачком в моменты
появления каких-то событий
(или прихода новой заявки,
или окончания обслуживания,
или момента, когда заявка, которой
надоело ждать, покидает очередь)
Слайд 5Предмет ТМО
построение математических моделей,
связывающих заданные условия работы СМО
(число
каналов, их производительность,
правила работы, характер потока заявок)
с показателями
эффективности СМО, описывающими
ее способность справляться
с потоком заявок
Слайд 6Показатели эффективности СМО
среднее число заявок, обслуживаемых
СМО
в единицу времени;
среднее число занятых каналов;
среднее число заявок в очереди и
среднее время ожидания обслуживания;
вероятность того, что число заявок
в очереди превысит какое-то значение,
и т. д.
Слайд 8Терминология ТМО
(по Кендаллу)
Для обозначения модели используют
3-5 символов:
| |
первый характеризует входной поток
требований, второй – распределение длительностей
обслуживания,
третий – число приборов в обслуживающей
системе
четвертый – допустимую длину очереди,
пятый – дисциплину обслуживания
требований.
Слайд 9Распределение вероятностей
M - экспоненциальное распределение;
D - детерминированное, или регулярное
распределение;
En - n-фазное распределение
Эрланга;G1 – рекуррентный характер входного потока (длительности интервалов статистически независимы и имеют одинаковое распределение) без каких-либо специальных предположений относительно функций распределения;
G - общий вид распределения длительностей
интервалов
Слайд 10Пример
M| D| 2
- экспоненциальное распределение времени между заявками (М),
регулярный характер обслуживания (D) и
два обслуживающих прибора
(2)Слайд 11Классификация СМО
по условию ожидания
СМО с отказами и СМО с
очередью
СМО с потерями (отказами);
СМО с ожиданием;
СМО с ограниченной длиной очереди;
СМО
с ограниченным временем ожидания. по числу фаз обслуживания –
однофазные и многофазные
по числу каналов –
одноканальные и многоканальные
по месту нахождения источника заявок -
«открытые» или «замкнутые»
Слайд 12Дисциплина обслуживания
в порядке поступления – FIFO, или
First In – First Out
в случайном порядке – Random
обслуживание с приоритетом – LIFO, или Last In – First Out
Приоритет
абсолютный
относительный
Слайд 13Потоки событий
Последовательность однородных событий, следующих одно за другим в
какие-то, вообще говоря, случайные моменты времени
Например,
поток вызовов на станции скорой помощи,
поток грузовых составов, поступающих на ж/д станцию,
поток неисправностей (сбоев) вычислительной машины,
поток отказов оборудования АЭС и т.д.
Слайд 14Свойства потоков
Поток событий называется регулярным, если события следуют одно
за другим через строго определенные промежутки времени.
Однако чаще приходится
встречаться с потоками событий, для которых и моменты наступления событий,
и промежутки времени между ними случайны
Слайд 15Стационарность
Поток событий называется стационарным, если вероятность попадания того
или иного числа событий на участок времени длиной τ зависит
только от длины участка и не зависит от того, где именно на оси (0,t) расположен этот участок.λ - интенсивность потока событий –
- среднее число событий в единицу времени
λ=const
Свойства потоков
Слайд 16Беспоследействие
Поток событий называется
потоком без последействия,
если для любых непересекающихся
участков
времени
число событий, попадающих на один из них,
не
зависит от того, сколько событий попало на другие
Слайд 17Ординарность
Поток событий называется ординарным,
если вероятность попадания на
элементарный участок Δt
двух или более событий
пренебрежимо мала по сравнению с вероятностью попадания одного событияСлайд 18Простейший поток
Поток событий, обладающий всеми тремя свойствами, -
стационарный,
без последействия,
ординарный –
называется простейшим, или
стационарным пуассоновским
Слайд 19Пуассоновский поток
Вероятность попадания на участок длиной τ ровно
m событий
(m=0,1,…)
где а - среднее число событий, приходящееся на участок τ
Слайд 21 Промежуток времени Т
между соседними событиями
в простейшем потоке
распределен
по экспоненциальному закону
с параметром λ
Слайд 22Ординарность
P0(Δt) - вероятность того, что на участке Δt не будет
ни одного события,
P1(Δt) - вероятность того, что на нем
появится одно событиеP1(Δt) ≈λΔt
Слайд 24Уравнения Колмогорова
Состояния системы с дискретными состояниями и непрерывным временем изменяются
в моменты прихода требований,
в моменты обслуживания требований или
в
моменты, когда требование покидает систему необслуженным Тогда процесс, происходящий в системе, может быть описан непрерывной марковской цепью
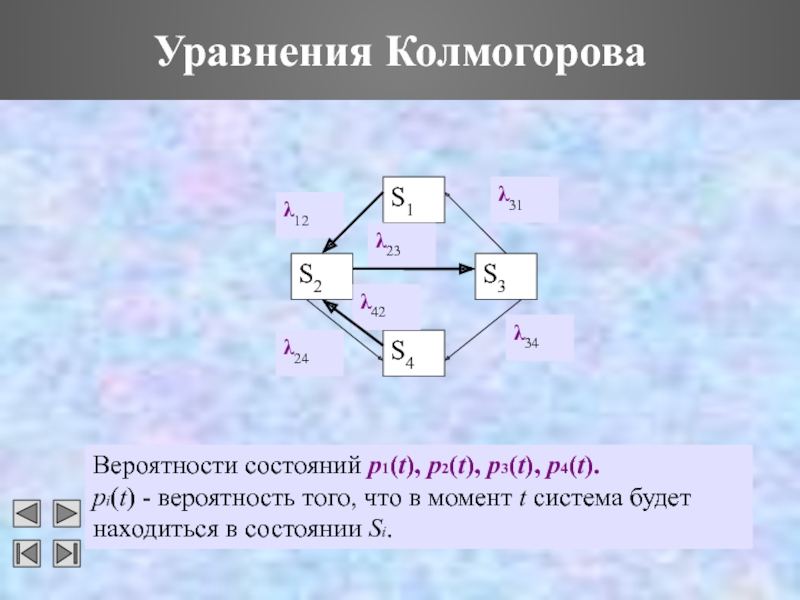
Слайд 25Уравнения Колмогорова
Вероятности состояний p1(t), p2(t), p3(t), p4(t).
pi(t) - вероятность того,
что в момент t система будет находиться в состоянии Si.
Слайд 26Уравнения Колмогорова
Придадим t малое приращение Δt и найдем вероятность того,
что в момент (t+Δt) система будет находиться в состоянии S1.
Как это событие может произойти?
1) в момент t система уже была в состоянии S1, а за
время Δt не вышла из этого состояния,
2) в момент t система была в состоянии S3, а за
время Δt перешла из него в S1.
Слайд 27Уравнения Колмогорова
В левой части каждого
уравнения стоит производная вероятности состояния,
а правая часть
содержит столько членов, сколько стрелок связано с этим состоянием. Если стрелка направлена из состояния, то соответствующий член имеет знак минус, если в состояние, то знак плюс.
Каждый член равен произведению плотности вероятности перехода, соответствующей данной стрелке, на вероятность того состояния,
из которого исходит стрелка