Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Спецкурс Microsoft Excel в профильном обучении
Содержание
- 1. Спецкурс Microsoft Excel в профильном обучении
- 2. Планпонятие матрицы;математическое содержание основных операций над матрицами;выполнения
- 3. Матрицы и основные операции над нимиМатрица
- 4. Умножение матрицы на числоНа заданное число умножается каждый элемент матрицы.
- 5. Сложение матрицСкладывают матрицы одинаковых размерностей. В результате
- 6. Умножение матрицПусть (аі1,..., аіп) — і-я
- 7. с11 =13 + 2 2 +
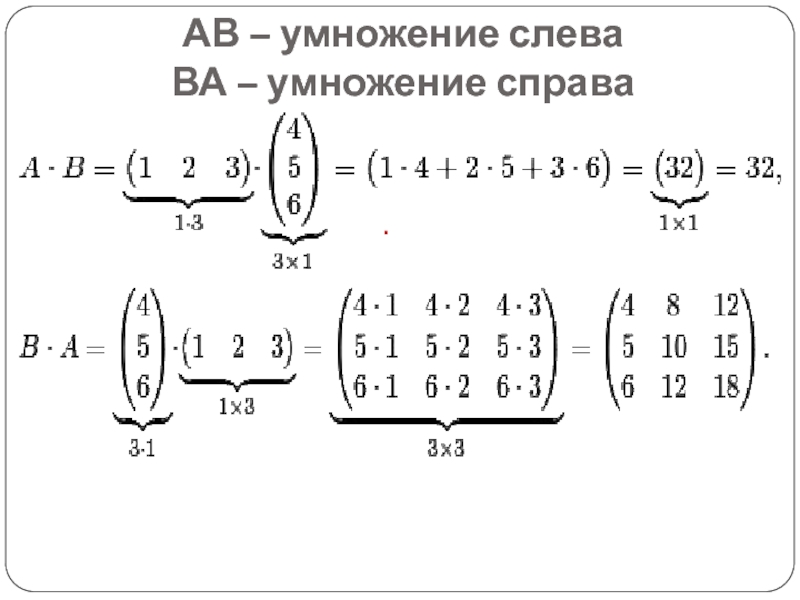
- 8. .АВ – умножение слеваВА – умножение справа
- 9. Квадратная матрицаГлавная диагональПобочная диагональКвадратная – матрица, у
- 10. Единичная матрицаЕдиничная – матрица, у которой на
- 11. Обратная матрицаМатрица А-1 называется обратной матрице А,
- 12. Определитель матрицыОпределитель – число, получаемое из матрицы
- 13. Обратная матрица
- 14. Операции с матрицами в MsExcelРезультат – диапазон
- 15. Операция умножения матрицы на числоЕсли матрица умножается
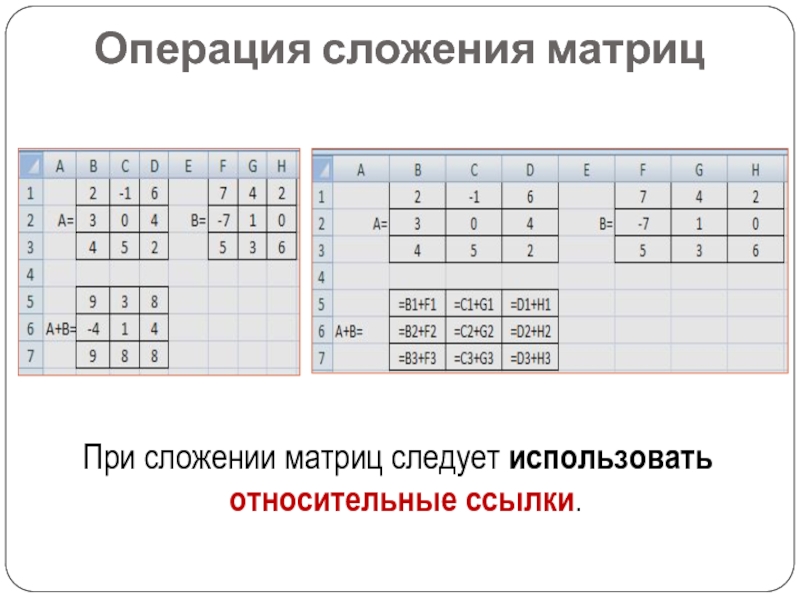
- 16. При сложении матриц следует использовать относительные ссылки.Операция сложения матриц
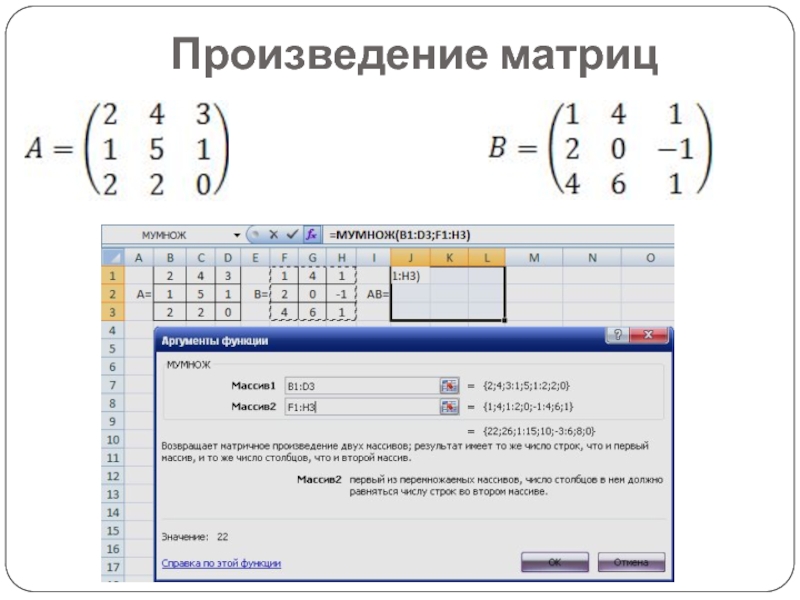
- 17. Произведение матриц
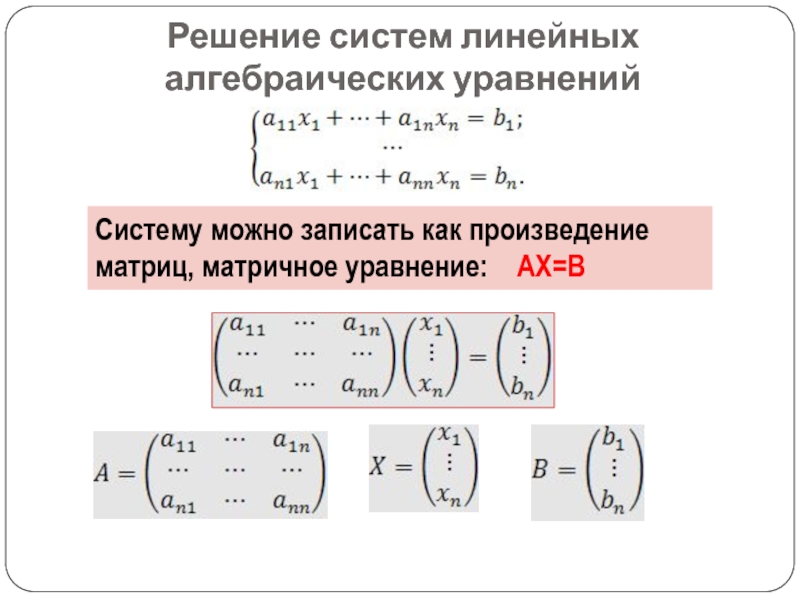
- 18. Решение систем линейных алгебраических уравненийСистему можно записать как произведение матриц, матричное уравнение: АХ=В
- 19. Решение систем линейных алгебраических уравненийУмножив первую строку
- 20. Правило решения системы линейных алгебраических
- 21. Алгоритм решения системы линейных алгебраических
- 22. Скачать презентанцию
Планпонятие матрицы;математическое содержание основных операций над матрицами;выполнения операций над матрицами в MsExcel;применение матриц для решения прикладных задач.
Слайды и текст этой презентации
Слайд 2План
понятие матрицы;
математическое содержание основных операций над матрицами;
выполнения операций над матрицами
в MsExcel;
Слайд 3Матрицы
и основные операции над ними
Матрица – прямоугольная таблица, в
каждой ячейке которой записано число – элемент матрицы.
Каждый элемент матрицы
имеет два индекса: номер строки и номер столбца, на пересечении которых он расположен . Элементы матрицы обозначают маленькими латинскими буквами, у которых в виде подстрочных знаков записывают индексы .
Матрица А имеет следующие элементы:
а11 = 5; а12 = – 7; а13 = 3; а21 = 4; а22 = 2; а23 = 9.
Размерность – одна из основных характеристик матрицы, количество строк и столбцов в ней.
А 2 х 3 (два на три).
Слайд 5Сложение матриц
Складывают матрицы одинаковых размерностей.
В результате получаем матрицу, каждый
элемент которой равен сумме соответствующих элементов матриц.
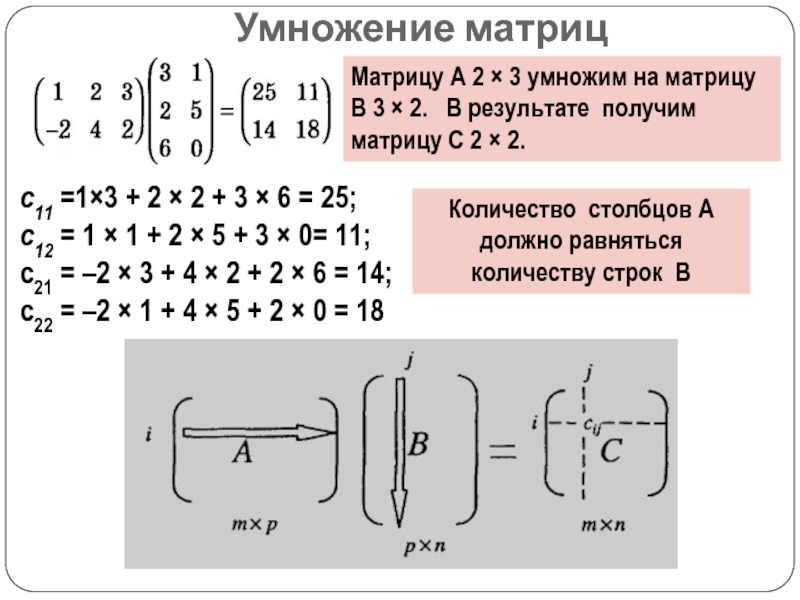
Слайд 6Умножение матриц
Пусть (аі1,..., аіп) — і-я строка А, а
— j-й столбец матрицы
В.В матрице С = АВ элемент с индексами ij вычисляется по формуле
Он равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В.
Каждая строка первой «множиться» на каждый столбец второй матрицы.
Слайд 7с11 =13 + 2 2 + 3 6
= 25;
с12 = 1 1 + 2 5
+ 3 0= 11;с21 = –2 3 + 4 2 + 2 6 = 14;
с22 = –2 1 + 4 5 + 2 0 = 18
Умножение матриц
Матрицу А 2 3 умножим на матрицу В 3 2. В результате получим матрицу С 2 2.
Количество столбцов А должно равняться количеству строк В
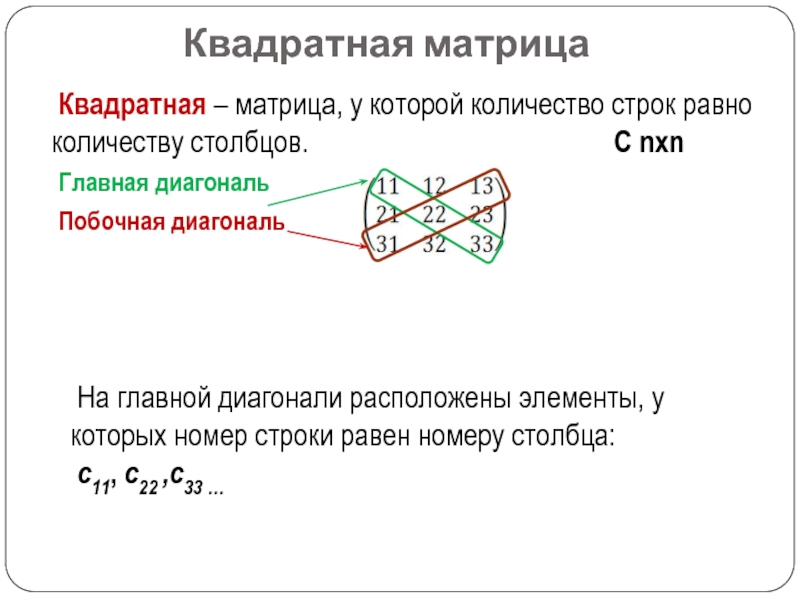
Слайд 9Квадратная матрица
Главная диагональ
Побочная диагональ
Квадратная – матрица, у которой количество строк
равно количеству столбцов.
С nxnНа главной диагонали расположены элементы, у которых номер строки равен номеру столбца:
с11, с22 ,с33 …
Слайд 10Единичная матрица
Единичная – матрица, у которой на главной диагонали расположены
единицы, а остальные элементы равны нулю.
Е 3 3
Е 2 2АЕ=ЕА=А
Слайд 11Обратная матрица
Матрица А-1 называется обратной матрице А,
если А-1А=Е, т.е.
их произведение, равно единичной матрице.
Обратные:
Слайд 12Определитель матрицы
Определитель – число, получаемое из матрицы по определенному правилу.
Определитель показывает, существует ли обратная матрица.
Если |А|=0, то обратная матрица
не существует.
Слайд 14Операции с матрицами в MsExcel
Результат – диапазон значений
Аргументами всех этих функций является диапазоны, содержащие элементы матриц по одному в каждой ячейке.
Следует выделить весь диапазон, где содержатся результаты, ввести формулу функции и нажать клавиши
Ctrl + Shift + Enter
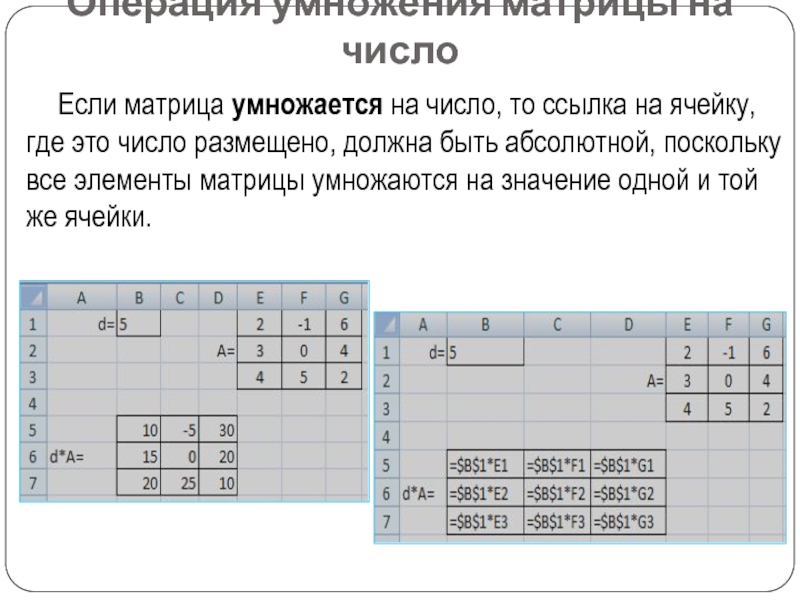
Слайд 15Операция умножения матрицы на число
Если матрица умножается на число, то
ссылка на ячейку, где это число размещено, должна быть абсолютной,
поскольку все элементы матрицы умножаются на значение одной и той же ячейки.
Слайд 18Решение систем линейных алгебраических уравнений
Систему можно записать как произведение матриц,
матричное уравнение: АХ=В
Слайд 19Решение систем линейных алгебраических уравнений
Умножив первую строку матрицы А на
первый столбец матрицы X (он в этой матрице один), получим
выражениеа11 х1 + … + а1nхn,
Умножив вторую строку А на столбец X , получим выражение
а21х1 + ... + а2пхп и т. д.
Каждое из этих выражений приравнивается соответствующему коэффициенту b1 , b2 …
Получим заданную систему
уравнений.
Слайд 20
Правило решения системы линейных алгебраических уравнений.
Для матричных уравнений выполняются
те же тождества, и для обычных уравнений .
В частности,
обе части матричного уравнения можно умножить на одну и ту же матрицу (справа или слева) . Умножим АХ = В на матрицу А-1,
получим А-1АХ = А-1В ЕХ = А-1В
Х = А-1В .
Слайд 21
Алгоритм решения системы линейных алгебраических уравнений в MSExcel.
Найдем матрицу
А-1
Вычислим определитель.
Если |А|≠0, то вычислим произведение А-1В
МОБР
МОПРЕД
МУМНОЖ
!
