Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Способы задания и свойства числовых последовательностей. Бесконечно убывающая
Содержание
- 1. Способы задания и свойства числовых последовательностей. Бесконечно убывающая
- 2. Числовая последовательность – это множество чисел, каждому из
- 3. Определение 1. Функцию вида у= f (х),
- 4. Свойства числовых последовательностейПоследовательность {an} называется монотонной, если an+1≥ an или an+1≤an
- 5. Если существует такое натуральное T, что, начиная с некоторого n,
- 6. Примеры бесконечных числовых последовательностей1, 2, 3, 4,
- 7. Способы задания числовых последовательностейСловесныйАналитическийРекуррентный
- 8. Словесный способ.Правило задания описано словами, без указания
- 9. Слайд 9
- 10. Продолжите ряд: 1, 10, 3, 9, 5,
- 11. Продолжите ряд: 1, 10, 3, 9, 5,
- 12. Аналитический способ задания числовых последовательностейПоследовательность задана аналитически,
- 13. Рекуррентный способ задания числовых последовательностейРекуррентный способ задания
- 14. 1, 1, 2, 3, 5, 8, 13,
- 15. Последовательность чисел ФибоначчиФиллотаксис (листорасположение)
- 16. Арифметическая прогрессия Пример: 1,
- 17. Слайд 17
- 18. Геометрическая прогрессия Пример: 54 , 18,
- 19. Развитие учения о прогрессиях Прогрессия (от
- 20. Задача 1.В благоприятных условиях бактерии размножаются так,
- 21. Решение:1). Выпишите последовательность в соответствии с условием
- 22. Задача 2 Найдите закономерности и покажите
- 23. Найдите закономерности и покажите их с
- 24. Задача 3 Определить, какие числовые последовательности являются
- 25. Сравним наши ответы:Геометрическая прогрессия – 3, 6.Арифметическая прогрессия
- 26. Геометрическая прогрессия {bn} - это числовая последовательность,
- 27. Вернемся к нашей последней прогрессии q=−3, а
- 28. Бесконечно убывающая геометрическая прогрессия.Совсем недавно мы говорили
- 29. Свойство арифметической прогрессии.an=(an+1+an−1)/2 - свойство членов арифметической
- 30.
- 31. Сумма членов геометрической прогрессии.
- 32. Формулы для прогрессий
- 33. Задача 5Ученик 5 А класса Вася, заболел
- 34. Домашнее задание:
- 35. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Способы задания и свойства числовых последовательностей.
Бесконечно убывающая геометрическая последовательность
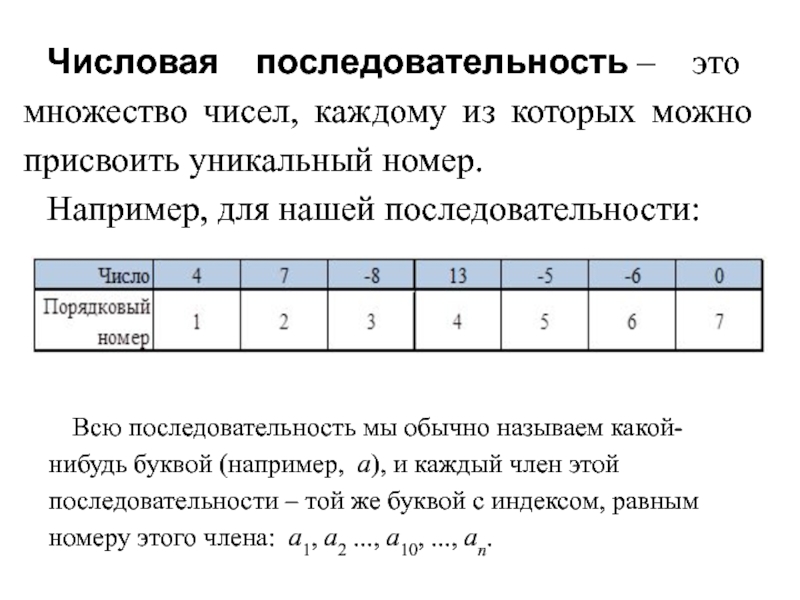
Слайд 2Числовая последовательность – это множество чисел, каждому из которых можно присвоить
уникальный номер.
буквой (например, a), и каждый член этой последовательности – той же буквой с индексом, равным номеру этого члена: a1, a2 ..., a10, ..., an.Слайд 3Определение 1.
Функцию вида у= f (х), х ϵ Ν
называют функцией натурального аргумента или числовой последовательностью и обозначают у
= f (n) или у1, у2, у3,…, уn,…, или (уn). (аn) – последовательность
а1 ; а2 ; а3 ;…. аn - члены последовательности Первый n-ый
член послед. член послед.
Последовательность
Слайд 4 Свойства числовых последовательностей
Последовательность {an} называется монотонной, если an+1≥ an или an+1≤an для всех n.
В
первом случае это монотонно неубывающая, во втором – монотонно невозрастающая
последовательность.Если an+1>an или an+1< an для всех n, то говорят, что последовательность {an} строго монотонна (возрастает в первом случаем и убывает во втором).
Последовательность {an} называется ограниченной, если существуют такие числа c и C, что для всех членов последовательности выполняются неравенства c ≤ an ≤ C.
Ограниченной сверху называется последовательность, для которой существует такое число C, что для всех членов последовательности выполняется неравенство an ≤ C.
Ограниченной снизу называется последовательность, для которой существует такое число c, что для всех членов последовательности выполняется неравенство an ≥ С.
Если говорят, что последовательность ограничена, это означает, что она ограничена и сверху и снизу.
Слайд 5Если существует такое натуральное T, что, начиная с некоторого n, выполняется равенство an = an+1, то
последовательность называется периодической, а T-длиной её периода.
Используя понятия монотонности, ограниченности и периодичности,
можно описать немало простейших свойств последовательностей. Вот некоторые из них:Если последовательность {an} монотонно возрастающая, то последовательность {-an} монотонно убывающая, и наоборот.
Если последовательность {an} монотонно невозрастающая, то последовательность {-an} монотонно неубывающая, и наоборот.
Монотонно возрастающая ограниченна снизу, монотонно убывающая – сверху.
Монотонно возрастающая или монотонно убывающая последовательность не может быть периодической.
Периодическая последовательность всегда ограничена.
Слайд 6Примеры бесконечных числовых последовательностей
1, 2, 3, 4, 5, … -
последовательность натуральных чисел.
2, 4, 6, 8, 10,… - последовательность чётных
чисел.1, 3, 5, 7, 9,… - последовательность нечётных чисел.
1, 4, 9, 16, 25,… - последовательность квадратов натуральных чисел.
2, 3, 5, 7, 11… - последовательность простых чисел.
Слайд 8Словесный способ.
Правило задания описано словами, без указания каких-либо формул или
когда закономерности между элементами последовательности нет.
Пример 1. Последовательность простых чисел:
2,3,5,7,11,13,17,19,23,29,31,… . Пример 2. Произвольный набор чисел:
1,4,12,25,26,33,39,… .
Пример 3. Последовательность четных чисел: 2,4,6,8,10,12,14,16,… .
Слайд 10Продолжите ряд: 1, 10, 3, 9, 5, 8, 7, 7,
9, 6…
Продолжите ряд 77, 49, 36, 18…
Примеры последовательностей.
Слайд 11Продолжите ряд: 1, 10, 3, 9, 5, 8, 7, 7,
9, 6…
Продолжите ряд 77, 49, 36, 18…
Ответ: Перемножаются
две цифры, входящиев предыдущее число
Ответ: Ряд состоит из двух частей: числа на нечетных местах: 1, 3, 5, 7, 9...; числа на четных местах: 10, 9, 8, 7
Примеры последовательностей.
Слайд 12Аналитический способ задания числовых последовательностей
Последовательность задана аналитически, если указана формула
n-ого члена.
Например,
yn=n2 – аналитическое задание последовательности 1, 4, 9,
16, …2) yn=С – постоянная (стационарная) последовательность
2) yn=2n – аналитическое задание последовательности 2, 4, 8, 16, …
Слайд 13Рекуррентный способ задания числовых последовательностей
Рекуррентный способ задания последовательности состоит в
том, что указывают правило, позволяющее вычислить n-ый член, если известны
ее предыдущие членыарифметическая прогрессия задается рекуррентными соотношениями a1=a, an+1=an + d
геометрическая прогрессия b1=b, bn+1=bn * q
Слайд 141, 1, 2, 3, 5, 8, 13, 21, 34, 55,
89, 144, 233, 377, 610…
Числа Фибоначчи.
Элементы числовой последовательности, в
которой каждое последующее число равно сумме двух предыдущих чисел. Леонардо Фибоначчи - итальянский математик.
(родился около 1170 — умер после 1228),
Последовательность Фибоначчи рекуррентно задать легко, а аналитически – трудно.
Слайд 15Последовательность
чисел Фибоначчи
Филлотаксис (листорасположение) — правило, по которому
располагаются, например, семечки в соцветии подсолнуха.
Семечки упорядочены
в два
ряда спиралей, один из которых идет
по часовой стрелке,
другой против неё.
Слайд 16 Арифметическая прогрессия
Пример: 1, 3, 5, 7,
9, 11, … возрастающая арифметическая прогрессия, у которой
d = 2.Числовую последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и одного и того же числа d, называют арифметической прогрессией, а число d – разностью арифметической прогрессии.
an+1 = an + d , n є N
d = an+1 - an
Слайд 18Геометрическая прогрессия
Пример: 54 , 18, 6, 2, …
-убывающая
геометрическая прогрессия,
у которой q
= 1/3.Числовую последовательность, все члены которой отличны от нуля и каждый член которой, начиная со второго, получается из предыдущего члена умножением на одно и то же число q, называют геометрической прогрессией, а число q – знаменателем геометрической прогрессии.
bn = bn - 1 · q
bn = b1 · qn - 1
Слайд 19
Развитие учения о прогрессиях
Прогрессия (от латинского progressio) -«движение вперёд»
Наблюдая луну
от новолуния до полнолуния, вавилоняне пришли к такому выводу: в
первые пять дней после новолуния рост освещения лунного диска совершается по закону геометрической прогрессии со знаменателем 2.Слайд 20Задача 1.
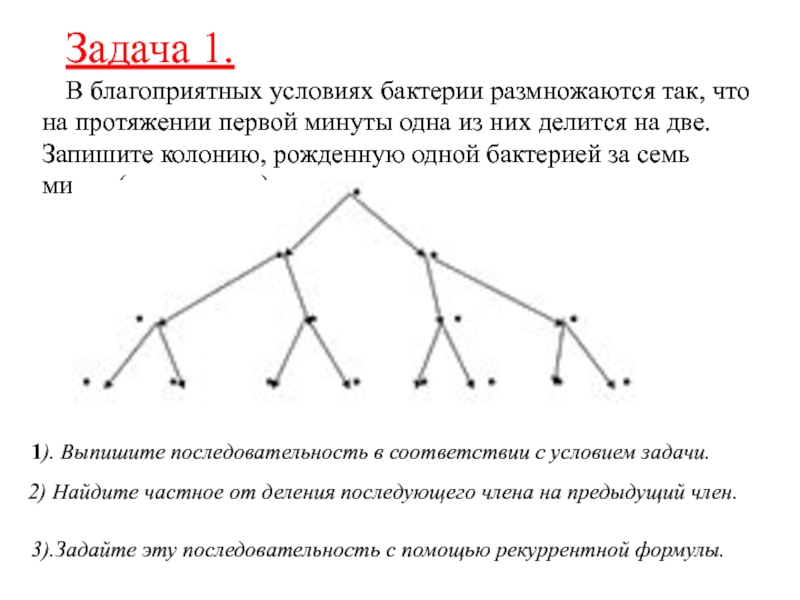
В благоприятных условиях бактерии размножаются так, что на протяжении
первой минуты одна из них делится на две. Запишите колонию,
рожденную одной бактерией за семь минут.(см. рисунок).1). Выпишите последовательность в соответствии с условием задачи.
2) Найдите частное от деления последующего члена на предыдущий член.
3).Задайте эту последовательность с помощью рекуррентной формулы.
Слайд 21Решение:
1). Выпишите последовательность в соответствии с условием задачи.
1;2;4;8;16;32;64.
или (bп)
- последовательность,
b1 =1; b2=2;
b3=4; b4=8; b5=16; b6 =32; b7 =64; 2) Найдите частное от деления последующего члена на предыдущий член.
b3 : b2 =4 : 2=2 ;
b4 : b3 =8 : 4=2;
b5 : b4 = 16 : 8=2; и т.д. bп+1: b п = q q -знаменатель прогрессии.
q = b2:b1= b3:b2=b4:b3=…= bп+1: b п
3).Задайте эту последовательность с помощью рекуррентной формулы.
b2 = 2b1
b3= 2 b2
b4= 2b3…..
bп+1 = q b п
Такую последовательность в математике называют геометрической прогрессией.
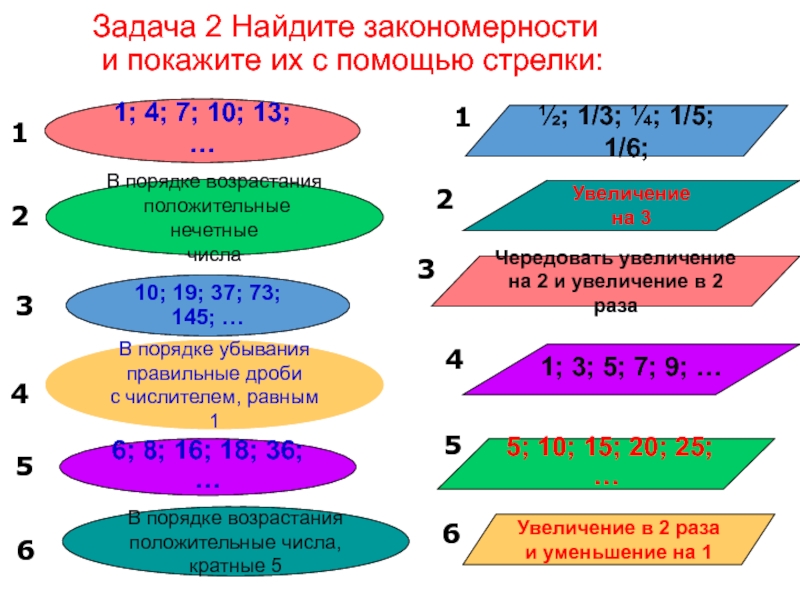
Слайд 22Задача 2 Найдите закономерности
и покажите их с помощью стрелки:
1;
4; 7; 10; 13; …
В порядке возрастания
положительные нечетные
числа
10;
19; 37; 73; 145; …
В порядке убывания
правильные дроби
с числителем, равным 1
6; 8; 16; 18; 36; …
В порядке возрастания
положительные числа,
кратные 5
½; 1/3; ¼; 1/5; 1/6;
Увеличение
на 3
Чередовать увеличение
на 2 и увеличение в 2 раза
1; 3; 5; 7; 9; …
5; 10; 15; 20; 25; …
Увеличение в 2 раза
и уменьшение на 1
1
2
3
4
5
6
1
2
3
4
5
6
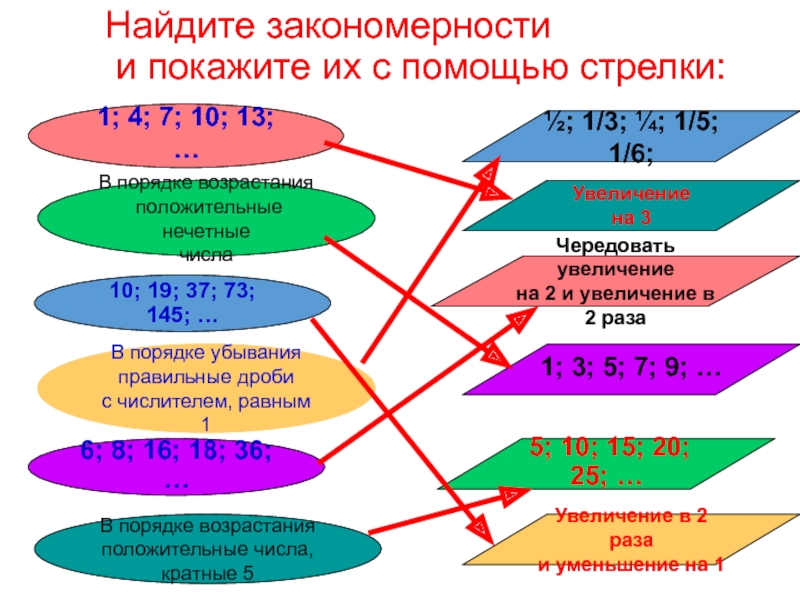
Слайд 23Найдите закономерности
и покажите их с помощью стрелки:
1; 4; 7;
10; 13; …
В порядке возрастания
положительные нечетные
числа
10; 19; 37;
73; 145; …
В порядке убывания
правильные дроби
с числителем, равным 1
6; 8; 16; 18; 36; …
В порядке возрастания
положительные числа,
кратные 5
½; 1/3; ¼; 1/5; 1/6;
Увеличение
на 3
Чередовать увеличение
на 2 и увеличение в 2 раза
1; 3; 5; 7; 9; …
5; 10; 15; 20; 25; …
Увеличение в 2 раза
и уменьшение на 1
Слайд 24Задача 3
Определить, какие числовые последовательности являются геометрической прогрессией, а
какие арифметической:
3; 6; 12; 24; 48; 56…
1; 12; 23; 34; 45 …
−99; 33; −11…
−6; 5; 17; 28; 39…
64; 16; 4; 1…2; 4; 8; 18…
Слайд 25Сравним наши ответы:
Геометрическая прогрессия – 3, 6.
Арифметическая прогрессия – 2, 4.
Не
является ни арифметической, ни геометрической прогрессиями - 1, 5, 7.
Слайд 26Геометрическая прогрессия {bn} - это числовая последовательность, первый член которой
отличен от нуля, а каждый член, начиная со второго, равен
предыдущему, умноженному на одно и то же число q ≠ 0. Это число называют знаменателем геометрической прогрессии.Как вы думаете, каким может быть q?
Положительным и отрицательным, но не нулем. Допустим, что q у нас положительное. Пусть в нашем случае q=3, а b1=4.
Чему равен второй член b2 и b3?
b2=4⋅3=12
b3=12⋅3=36
Соответственно, q>0, то все последующие члены прогрессии имеют одинаковый знак – они положительны.
А что если q отрицательное? Например, q=−3, а b1=4. Чему равен второй член b2 и b3?
b2=4⋅(−3)=−12
b3=−12⋅(−3)=36
Если q<0, то знаки членов геометрической прогрессии чередуются.
q – это число, во сколько раз изменяется каждый последующий член геометрической прогрессии.
Слайд 27Вернемся к нашей последней прогрессии q=−3, а b1=4 и попробуем так
же как и в арифметической найти ее 6 член. Как вы уже
догадываетесь, есть два способа его нахождения.Последовательно умножаем каждый член на q.
b2=b1⋅ q =4⋅−3=−12
b3= b1⋅ q ⋅ q = b1⋅ q2 =−12⋅(−3)=36
b4= b1⋅ q ⋅ q⋅ q= b1⋅ q3 =36⋅(−3)=−108
b5= b1⋅ q4 =−108⋅(−3)=324
b6= b1⋅ q5 = 324⋅(−3)=−972
Вывод: Если нам нужно найти значение числа прогрессии с порядковым номером, то мы умножаем первый член геометрической прогрессии b1 на знаменатель q в степени, которая на 1 единицу меньше, чем порядковый номер искомого числа.
b4=4⋅(−3)4−1=4⋅(−3)3=−108
b6=b1⋅q 6−1
b6=4⋅(−3)6−1=4⋅(−3)5=−972
Приведем формулу в общий вид и получим:
bn=b1⋅qn−1 - уравнение членов геометрической прогрессии.
Слайд 28Бесконечно убывающая геометрическая прогрессия.
Совсем недавно мы говорили о том, что
q может быть как больше, так и меньше нуля, однако, есть
особые значения q при которых геометрическая прогрессия называется бесконечно убывающей. При −1Для начала запишем какую-нибудь геометрическую прогрессию, состоящую из 5 членов.
Допустим, b1=1, а q=1/2, тогда:
bn=b1⋅q n−1
b2=1⋅1/2=1/2
b3=1/2⋅1/2=1/4
b4=1/4⋅1/2=1/8
b5=1/8⋅1/2=1/16
Мы видим, что каждый последующий член меньше предыдущего в 1/2 раза, но будет ли какое-либо число bn=0? Вы сразу же ответите – «нет». Вот поэтому и бесконечно убывающая – убывает, а нулем никогда не становится.
Слайд 29Свойство арифметической прогрессии.
an=(an+1+an−1)/2 - свойство членов арифметической прогрессии.
Свойство геометрической прогрессии.
Как найти b3, зная b2 и b4?
Умножим
b2⋅b4=b1⋅q ⋅b1⋅q3= b12⋅q4
1)
b2⋅b4=b12⋅q4 2) b3=b1⋅q2 следовательно b3=b2⋅b4 Почему?
((из 1) следует b12= b2⋅b4/ q4 , следовательно b1=b2⋅b4q4 подставим b1 в 2) и сократим q))
свойство членов геометрической прогрессии
Слайд 33Задача 5
Ученик 5 А класса Вася, заболел гриппом, но продолжает
ходить в школу. Каждый день Вася заражает двух человек, которые, в
свою очередь, заражают еще двух человек и так далее. Всего в классе 31 человек. Через сколько дней гриппом будет болеть весь класс?Итак, первый член геометрической прогрессии это Вася, то есть 1 человек. 2 -ой член геометрической прогрессии, это те два человека, которых он заразил в первый день своего прихода. Общая сумма членов прогрессии равна количеству учащихся 5А. Соответственно, мы говорим о прогрессии, в которой:
Весь класс заболеет за 5 дней.