Слайд 13. Статистические функции распределения
3.1. Понятия о статистическом законе распределения
3.1.1. Дискретные
функции распределения
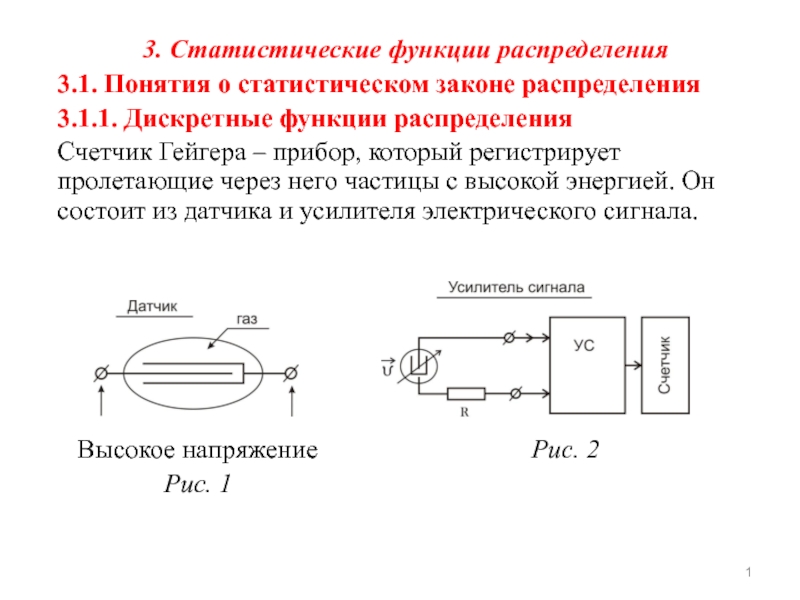
Счетчик Гейгера – прибор, который регистрирует пролетающие через него
частицы с высокой энергией. Он состоит из датчика и усилителя электрического сигнала.
Высокое напряжение Рис. 2
Рис. 1
Слайд 2 В момент прохождения частицы с высокой энергией счетчик
воспринимает сигнал с усилителя сигнала УС и
пересчитывает число частиц.
В течение заданного интервала
времени схема фиксирует количество пролетевших
через счетчик частиц . Затем счетчик запускается снова
на время и идет запись полученных значений в таблицу
- число частиц, появившихся за интервал времени .
При этом время изменяется в пределах от до .
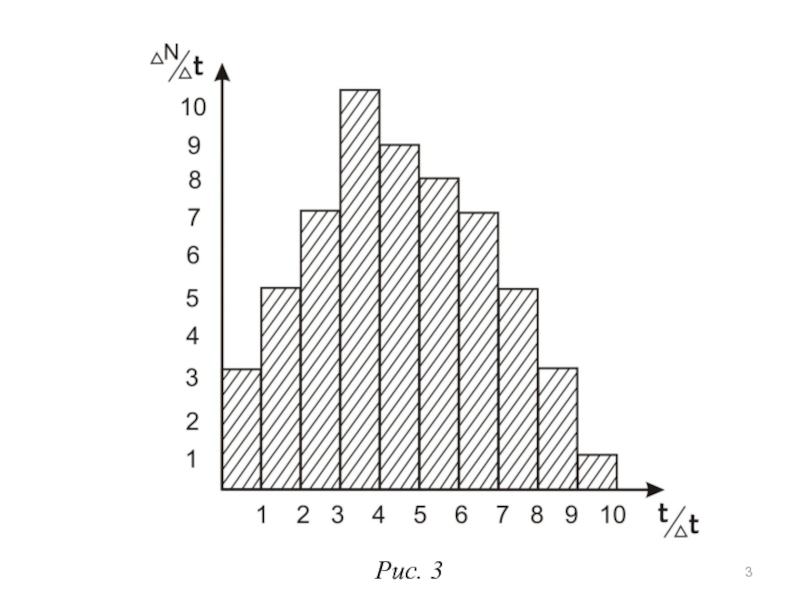
Строим график (см. рис. 3)
- называется дискретной
функцией распределения
(математики называют его
гистограммой). Она показывает: какое число
быстрых частиц пролетело через счетчик в момент
времени от до . Из графика видно, что если
t=0, то от 0 до их было 3 частицы, а от момента времени до их было 10 частиц.
Слайд 5 Если сложить площадь всех столбиков на графике:
- полное число частиц, пролетевших через
счетчик (1)
N=3+5+7+10+9+8+7+5+3+1=58 частиц.
Можно ввести нормированную на число частиц дискретную
функцию распределения:
(2)
Если полное число частиц (1) поделить на N, то получим
условие нормировки функции распределения
(3)
Слайд 6 Функция (2) показывает какая доля частиц пролетает через
счетчик в момент времени от до
. В интервале от 0 до
их , в интервале от до их .
3.1.2. Непрерывные функции распределения.
Если в дискретной функции распределения устремить
, то , а и тогда - будет
непрерывной функцией распределения. Такой переход
возможен только при наличии огромного числа
регистрируемых частиц. В идеальном газе и
поэтому такой переход допустим.
Тогда, для большого N можно ввести вероятность того, что
величина x, характеризующая какой- либо физический
параметр, лежит в интервале значений от x до .
, (4)
где - нормированная на число частиц, непрерывная
функция распределения по значениям величины х.
Условие нормировки:
(5)
по возможному интервалу значений, принимаемому
переменной х.
Если х играет роль объема, то - плотность вероятности;
если х- координата, то - вероятность, отнесённая к
интервалу длины; если х - скорость, то - вероятность,
отнесенная к интервалу скорости и т. д.
Если в газе N молекул, а - доля частиц, для которых
физическая величина х заключена в интервале от х до ,
Слайд 8то вероятность, выраженная через долю частиц, имеет вид:
(6)
Отсюда, количество молекул , для которых величина х,
характеризующая их, заключена в интервале значений от х, до
, равна:
(7)
Вычисление средних значений по функции распределения
(ФР)
Если число частиц велико, то это ансамбль частиц. Среднее
значение физической величины по ансамблю:
либо , если выполнено
уравнение нормировки (5).
, если выполнено (5).
Слайд 93.2. Функции распределения молекул по скоростям
в газе.
Молекулы газа,
находящегося в равновесии движутся с
самыми различными скоростями, причем как
модуль так и
направление их скорости непрерывно изменяются из-за
соударений. При нормальных условиях одна молекула
сталкивается с другими раз в секунду.
В газе различают две непрерывные функции распределения
молекул (N – число молекул):
1) По компоненте скорости
(8)
,
где m – масса одной молекулы, T- абсолютная температура, k-
постоянная Больцмана, - значение скорости молекул на
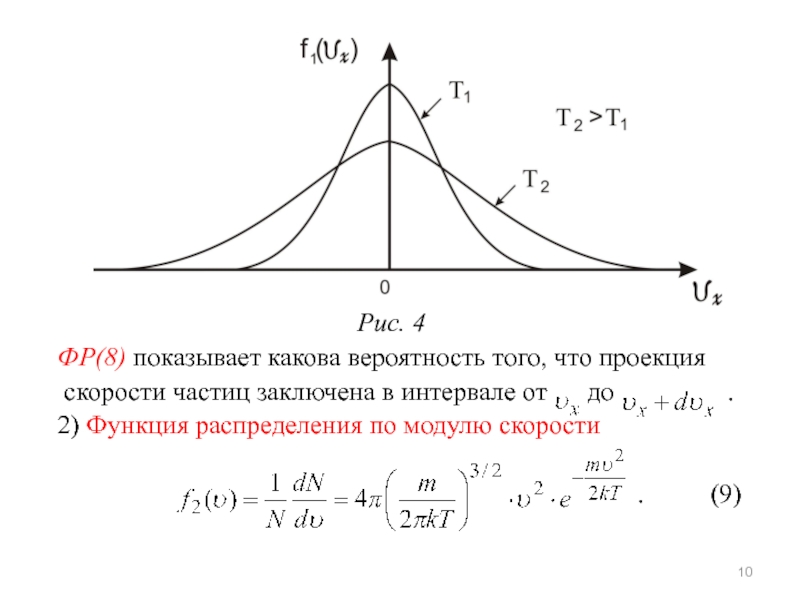
направление оси x в пространстве. Ее график на рис.4.
Рис. 4
ФР(8) показывает какова вероятность того, что проекция
скорости частиц заключена в интервале от до .
2) Функция распределения по модулю скорости
. (9)
Слайд 11
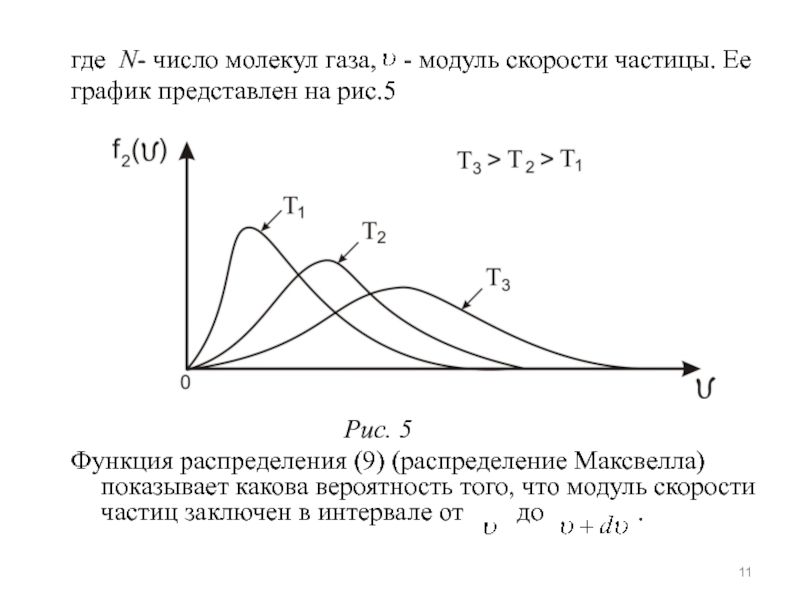
где N- число молекул газа, - модуль скорости частицы.
Ее
график представлен на рис.5
Рис. 5
Функция распределения (9) (распределение Максвелла) показывает какова вероятность того, что модуль скорости частиц заключен в интервале от до .
Слайд 12 Различие законов связано с тем, что
- указывает на
равновесность распределения молекул по направлениям в
пространстве: в пределах
любым образом ориентированного, но постоянного по величине телесного угла
в каждый момент времени лежат направления движения в среднем одинакового числа молекул , а второй утверждает, что возможные значения модуля скорости, заключенные от нуля до бесконечности, не равновероятны.
3.3. Следствия из закона распределения .
Модуль скорости, на который приходится максимум
функции распределения, называют наиболее вероятной
скоростью движения молекулы
- наиболее вероятная скорость.
2. Максимальное значение функции
.
При - максимум убывает с ростом
температуры.
3. Средний модуль скорости движения молекул
4. Средний квадрат скорости движения молекул
Слайд 144. ГАЗЫ В СИЛОВОМ ПОЛЕ
4.1 БАРОМЕТРИЧЕСКАЯ ФОРМУЛА
Рассмотрим идеальный газ, находящийся
в однородном поле силы тяжести при постоянной температуре.
Выделим
вертикальный столб газа с площадью поперечного сечения, равной единице. Тогда перепад давлений между нижним и верхним основаниями слоя будет равен весу этого слоя, т.е.
(1)
где ρ - плотность газа на высоте , - ускорение свободного падения.
Слайд 15Выражая плотность из
уравнения Менделеева-Клапейрона и подставляя её в (1), получим
(2).
Интегрирование приводит
к соотношению
(3)
где постоянная интегрирования выбрана в виде . После потенцирования будем иметь
(4)
Постоянную С определим из условия, что при ( - давление на высоте
Окончательно для зависимости давления от высоты имеем формулу
(5)
которая называется барометрической.
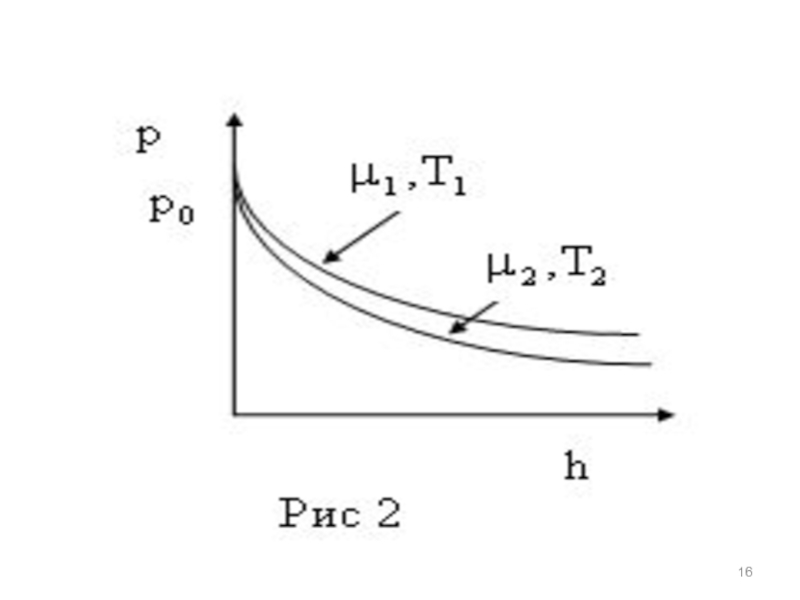
На рис. 2 изображены зависимости давления идеального газа от высоты для различных газов .
Слайд 17
m – масса одной молекулы.
(6)
Из него видно, что барометрическая формула описывает зависимость давления однокомпонентного идеального газа, находящегося в состоянии равновесия с постоянной температурой в однородном поле силы тяжести.
Подставляя в неё справа и слева уравнение Менделеева-Клапейрона ,
приходим к распределению Больцмана
.
(7)
Оно показывает какая связь существует между концентрацией частиц и их потенциальной энергией.
Больцманом было доказано, что выражение (7) справедливо не только для поля силы тяжести, но и для систем с большим числом частиц, находящихся в любых неоднородных потенциальных силовых полях в состоянии теплового равновесия.
Барометрическую формулу можно представить в виде