Слайд 1Статистические методы, оценивающие факторные эффекты и эффекты межфакторного взаимодействия
Общая
линейная модель
Метрические данные
Сравнение нескольких средних (>2): ANOVA (1ДА).
Оценка эффектов межгрупповых
и внутригрупповых факторов: многофакторный ДА (ОЛМ-одномерная, ОЛМ-повторные измерения).
Оценка межфакторного взаимодействия.
Оценка влияния факторов на несколько зависимых переменных (MANOVA, ОЛМ-многомерная).
Слайд 2Неметрические данные:
Только сравнение медиан нескольких выборок.
Непараметрические тесты для нескольких независимых
выборок.
Непараметрические тесты для нескольких связанных выборок.
Общая линейная модель.
Слайд 3Обобщенная линейная модель
Области применения
Метрические и неметрические данные:
Оценка факторных эффектов и
эффектов межфакторного взаимодействия для неметрических данных – номинальных (бинарных), мультиноминальных,
порядковых: Обобщенные линейные модели, Обобщенные уравнения оценки.
Обработка многоуровневых данных: смешанные модели с вложенными факторами: Смешанные модели (Линейная …, Обобщенные линейные).
Слайд 4Сущность и логика дисперсионного анализа
ДА или ANOVA (Analysis of Variance):
оценка факторных эффектов и межфакторных взаимодействий.
Состоит в разложении (анализе) дисперсии
одной или нескольких переменных на составляющие компоненты, сравнивая которые друг с другом с помощью F-критерия, можно оценить ее (их) вклад в общую вариацию данных.
Слайд 5Термины
Уровни НЗП или фактора – пол, возраст, уровень толерантности, место
жительства, профессия, вид тренинга и т.д.
Однофакторный ДА и многофакторный ДА
– сравнение групповых средних и дисперсий по каждому уровню фактора. Оценка главных эффектов.
Межфакторное взаимодействие – сравнение средних и дисперсий по каждому уровню одного фактору на каждом уровне другого фактора.
Ковариата – непрерывная (т.е. не дискретная, НЕ группирующая НЗП), включаемая в регрессионную модель.
Слайд 6Линейная модель ДА
Однофакторный ДА
X4,1 = общ. + Ф1 + 4,1
общ.
– среднее в популяции, Ф1 - вклад фактора группы 1,
4,1 - вклад уникальности 4-го испытуемого, ошибка модели.
Нулевая гипотеза:
H0 :общ = 1 = 2 = 3.
Допущения ДА:
Значения ЗП в каждой группе (выборке) нормально распределены вокруг своего среднего.
Равенство (однородность) дисперсий выборочных распределений, соответствующих каждому уровню фактора, т.е. 12 = 22 = 32.
Независимость наблюдений.
Слайд 7Последствия нарушения допущений ДА
Высокая устойчивость или робастность ДА. Особенно при
условиях:
1. Объемы выборок равны или отличаются незначительно.
2. Используются выборки
большого объема.
Критерии проверки однородности дисперсий: Шеффе, Ливинь и др.
Слайд 8Общая логика ДА или как работает ДА
Два варианта оценки общей
дисперсии данных:
Внутригрупповая дисперсия - s2WG: общая дисперсия есть среднее арифметическое
групповых дисперсий. Отражает влияние случайных факторов.
Межгрупповая (факторная) дисперсия - s2BG: отражает не случайную, а систематическую вариацию, т.е. является оценкой разброса самих выборочных (групповых) средних.
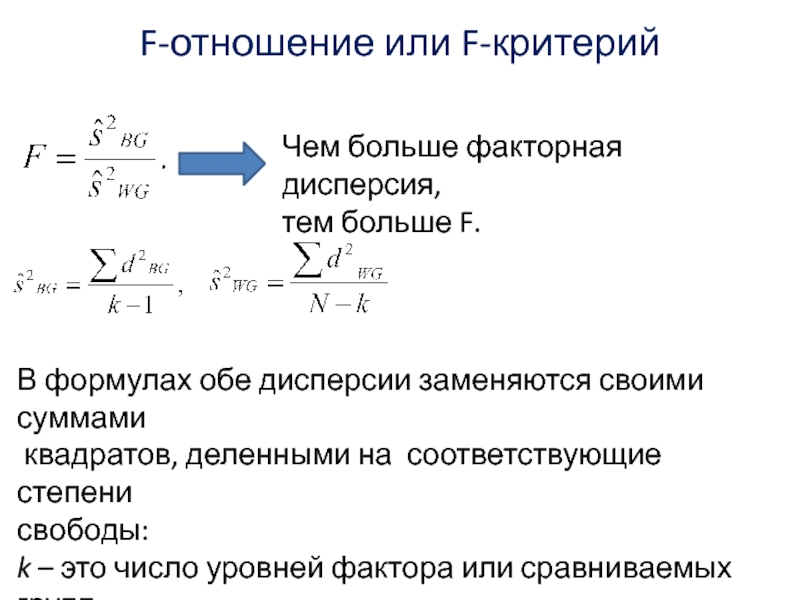
Слайд 9F-отношение или F-критерий
В формулах обе дисперсии заменяются своими суммами
квадратов,
деленными на соответствующие степени
свободы:
k – это число уровней фактора
или сравниваемых групп,
N – это число испытуемых.
Чем больше факторная дисперсия,
тем больше F.
Слайд 10Множественные сравнения средних
Используемые тесты, с учетом или без учета однородности
дисперсий выборок:
Шеффе
Бонферони
ЕНЗР
Хауэлла
Слайд 11Оценка силы факторного эффекта
Один из простейших - 2 (эта квадрат):
Более
точная, несмещенная оценка - 2 (омега квадрат):
Слайд 12Две модели ДА
В модели ДА с фиксированными эффектами исследователь намеренно
устанавливает строго определенные уровни изучаемого фактора.
В модели со случайными эффектами
уровни значения фактора выбираются исследователем случайно из широкого диапазона изменений фактора. Вложенные факторы. Нестинг-модели. Многоуровневые модели.
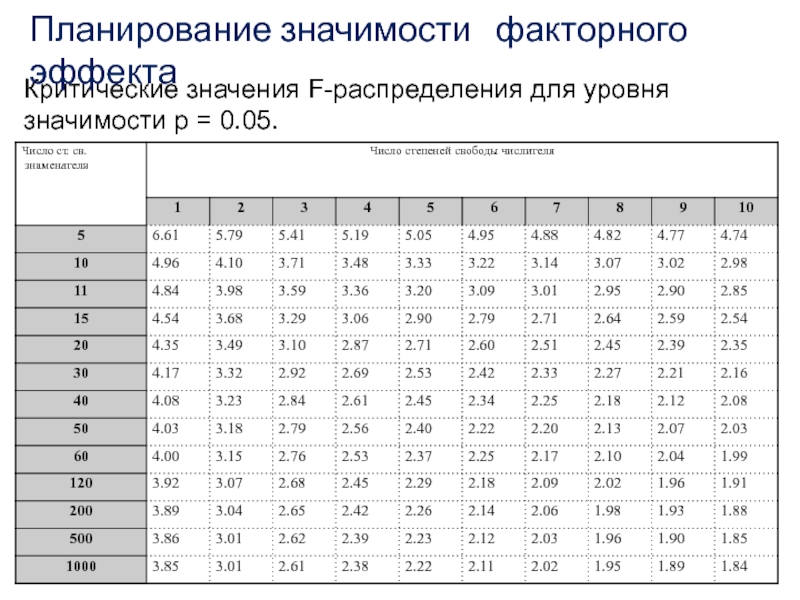
Слайд 13Критические значения F-распределения для уровня значимости p = 0.05.
Планирование значимости
факторного эффекта
Слайд 14Многофакторный дисперсионный анализ
Factorial Analysis of Variance, ОЛМ-одномерная.
Линейная модель ДА:
Xijg =
общ, + Фj + Фg + Фj *Фg +ijg
Формулировка статистических
гипотез:
Отдельно по фактору i: вариации средних по уровням фактора i – случайны.
Отдельно по фактору j: вариации средних по уровням фактора j – случайны.
Для взаимодействия факторов i и j:
влияние фактора i различно при разных уровнях фактора j, и наоборот.
Слайд 15Проблемы ДА с большим числом факторов:
X = общ, + Фj
+ Фg + Фk + Фj *Фg + Фj *Фk
+
+ Фi *Фk + Фi * Фj *Фk +ijk
Итого – 8 компонентов дисперсии…
Слайд 16ДА с повторными измерениями – ОЛМ-повторные измерения
Xij = общ. +
Фj +pi + Фj×pji +ij, где
pi - компонент, связанный с
влиянием индивидуальности i-го испытуемого, Фj×pji - дополнительный эффект взаимодействия этих двух компонент.
Особенность – данные повторных измерений связаны друг с другом, не являются независимыми. Следовательно можно и нужно учесть вклад индивидуальных различий испытуемых.
Преимущество: при вычислении знаменателя F-отношения – , из него вычитается межиндивидуальная вариация, получаются более высокие оценки.
Слайд 17MANOVA или ОЛМ-многомерная
Не требует допущения о сферичности.
Менее мощная процедура. Особенно
на малых выборках.
Предполагается связь между рядом ЗП.
Резоны: учет интеркорреляции между
ЗП-ми.
Допущения:
Многомерное нормальное распределение.
Для каждого уровня фактора ЗП образовывают одну и туже дисперсионно-ковариационную матрицу (квадратная матрица, на диагонали которой лежат дисперсии переменных, а ее элементами - коэффициенты ковариации между переменными).
Слайд 18Дополнительное допущение для
ДА с повторными измерениями
Допущение о симметричности ковариационной матрицы
уровней факторов (в б. общем плане - сферичности).
1 фактор, 3
уровня:
Слайд 19Что проверяем?
М-тест Бокса: оценка равенства дисперсионно-ковариационных матриц для каждого уровня
фактора (p>0,05).
Тесты Бартлетта, Моучли на сферичность: корреляционная матрица переменных не
является единичной матрицей, следовательно наши переменные связаны корреляционной связью (р<0,05).
Слайд 20А внутригрупповые факторы?
Есть возможность включать в многомерный ДА не только
межгрупповые, но и внутригрупповые факторы, однако она реализуется с помощью
специального командного режима выполнения статистических процедур (Comand Syntex).
Слайд 21Непараметрические процедуры
Ранговые критерии для сравнения нескольких выборок - аналоги классического
ДА.
Пример «работы» непараметрического критерия Фридмана. Основная идея: если между группами
нет различия, то а) ранжирование наблюдений будет случайным и б) средние ранги разных переменных будут примерно одинаковыми.
где К - число совпадающих наблюдений, j - число групп, Т - сумма рангов в каждой группе.
Слайд 22Классификация критериев
по типу решаемых задач
Критерии для несвязанных выборок
Н-критерий Краскела-Уоллеса
Медианный
критерий
Критерий Джонкхиера-Терпстры
Критерии для связанных выборок
Критеий Фридмана
W-критерий Кендала
Q-критерий Кокрена
Ограничение для Н-критерий
Краскела-Уоллеса: распределения имеют схожую форму.
Слайд 23Классификация критериев
по типу решаемых задач
Критерии для ранговых данных и критерий
для дихотомических (бинарных) переменных:
Для ранговых данных: Н-критерий Краскела-Уоллеса, Медианный критерий,
Критерий Джонкхиера-Терпстры, W-критерий Кендала, Критеий Фридмана.
Для дихотомических данных (0 или 1): Q-критерий Кокрена.
Слайд 24Классификация критериев
по типу решаемых задач
Критерии для простого сравнения выборок и
критерии, учитывающие определенную упорядоченность сравниваемых выборок:
Простое сравнение (менее мощные):
Н-критерий Краскела-Уоллеса, Медианный критерий, W-критерий Кендала, Критеий Фридмана
Учет упорядоченности (более мощный): критерий Джонкхиера-Терпстры, критерий Пейджа.
Выявляют различия там, где обычные критерии (Крускала-Уоллиса, Фридмана и др.) дают отрицательный результат.
Слайд 25Примеры эмпирических данных
Шкала экзистенции.sav – однофакторный ДА. Оценить значимость различий
3-х групп испытуемых (переменные – возраст и образование) по порядковым
шкалам SD, ST, P, F, EG.
Индивид и музыка. sav - непараметрический критерий для непарных выборок.
Оценить значимость различий по предпочтению музыки между группами испытуемых, различающихся по семейному положению, образованию и национальности c помощью подходящего непараметрического критерия для непарных выборок.
Слайд 26Примеры эмпирических данных
MANOVA.sav - процедура ОЛМ-многомерная.
Оценить значимость различий по факторам
«экстраверсия» и «нейротизм» а также эффект межфакторного взаимодействия. Оценить силу
оцениваемых эффектов, построить соответствующие графики и полезные таблицы.
Тренинг личностного роста_СЖО.sav.
Оценить влияния на шкалы опросника межгруппового фактора «Группа испытуемых» (контрольная и экспериментальная – которая проходила тренинг) и внутригруппового фактора «Время тестирования» (до тренинга и после тренинга).
Слайд 27Примеры эмпирических данных
Когнитивные стили, темперамент и СКИ.sav - процедуры ОЛМ-одноомерная
ОЛМ-многомерная.
Оценить значимость различий во времени решения задач 3-х уровней сложности
и общего времени в зависимости от 2-х когнитивных стилей, экстраверсии и нейротизма, их взаимодействия. Оценить силу оцениваемых эффектов, построить соответствующие графики и таблицы.