Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тайное знание теории групп: При записи соотношения слова пишутся по кругу
Содержание
- 1. Тайное знание теории групп: При записи соотношения слова пишутся по кругу
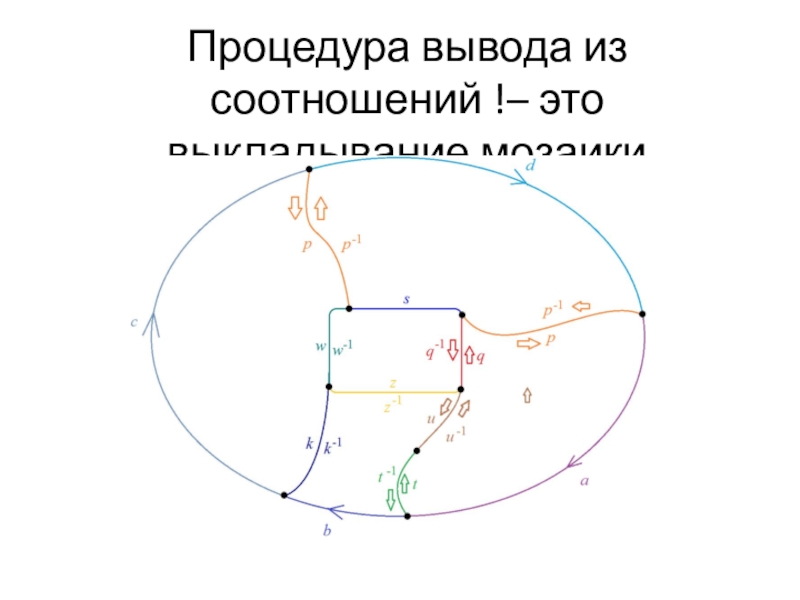
- 2. Процедура вывода из соотношений !– это выкладывание мозаики
- 3. Соотношение сформированное на границе есть следствие внутренних
- 4. Напоминалка.
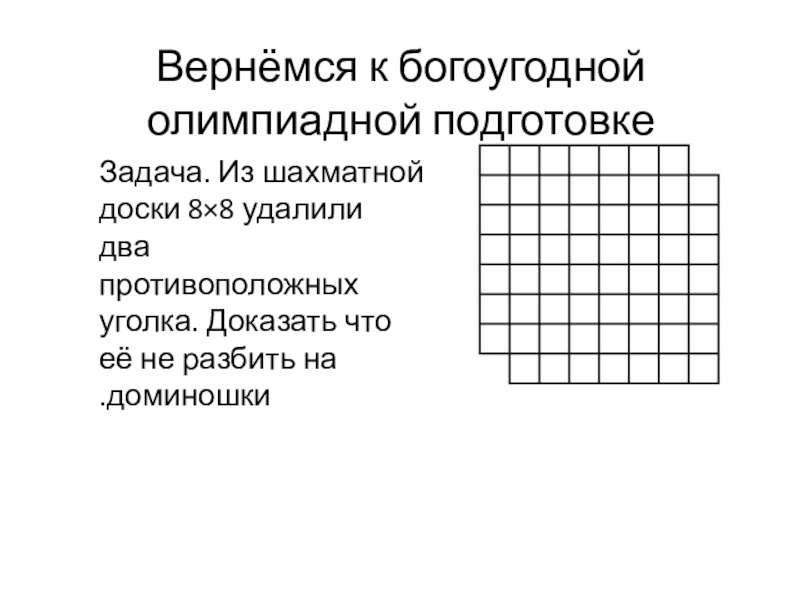
- 5. Задача. Из шахматной доски 8×8 удалили два
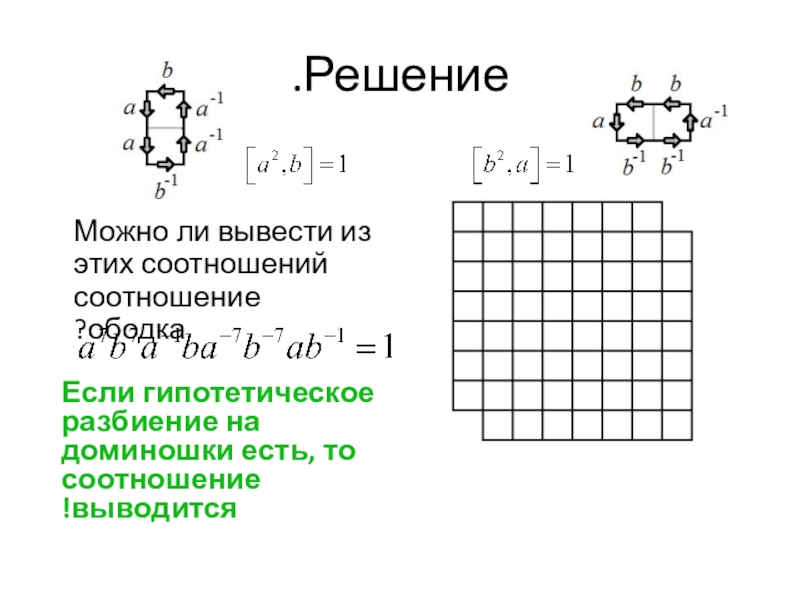
- 6. Решение.Можно ли вывести из этих соотношений соотношение ободка?Если гипотетическое разбиение на доминошки есть, то соотношение выводится!
- 7. Однако … Пусть а транспозиция (1 2)123а
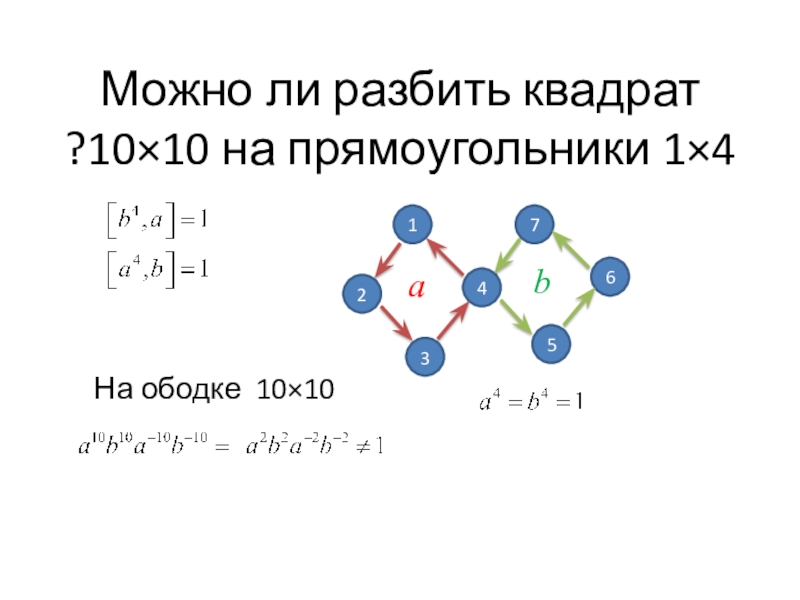
- 8. Можно ли разбить квадрат 10×10 на прямоугольники 1×4?7456123а bНа ободке 10×10
- 9. Упражнение 1. Прямоугольник m×k замощается прямоугольниками 1×n
- 10. Возражение: это стрельба из пушки по воробьям!Ответ:
- 11. Треугольник Т5Можно попробовать замостить Тn треугольничками
- 12. Задача 1. Тn замощается Т2
- 13. Задача 3. Фигуру F нельзя покрыть плитками
- 14. Задача 6. На острове Серобуромалин живут хамелеоны:
- 15. Задача 8. В клетках квадратной таблицы m×m
- 16. Задача 9. На табло стоят лампочки, каждая
- 17. Задача 11. (а) Можно ли круг разрезать
- 18. Задача 13. При каких m и n
- 19. Для дальнейщего чтения:https://www.turgor.ru/lktg/1996/lktg1996.pdf cтраницы 48-50https://www.turgor.ru/lktg/2009/4/index.phphttps://www.turgor.ru/lktg/2006/2/index.htmhttps://www.sciencedirect.com/science/article/pii/0097316590900574 (Конвей, Лагариас)http://www.mathnet.ru/php/presentation.phtml?option_lang=rus&presentid=7278
- 20. Слайд 20
- 21. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Тайное знание теории групп:
При записи соотношения
слова пишутся по кругу
Если круг
разрезать в любом другом месте, получится равносильное соотношение
Слайд 3Соотношение сформированное на границе есть следствие внутренних соотношений
Если некоторое
соотношение w = 1 является следствием соотношений wi
= 1 , то существует диаграмма в которой w написано на границе, а wi на клетках.Это просто
Это сложнее
Слайд 5Задача. Из шахматной доски 8×8 удалили два противоположных уголка. Доказать
что её не разбить на доминошки.
Вернёмся к богоугодной олимпиадной подготовке
Слайд 6Решение.
Можно ли вывести из этих соотношений соотношение ободка?
Если гипотетическое разбиение
на доминошки есть, то соотношение выводится!
Слайд 7Однако …
Пусть а транспозиция (1 2)
1
2
3
а
Пусть b транспозиция
(2 3)
b
Тогда
С другой стороны
А это цикл длины 3!
Слайд 9Упражнение 1. Прямоугольник m×k замощается прямоугольниками 1×n m
или k делится на n.
Упражнение 2. Квадрат 6×6 нельзя
разбить на прямоугольниками 1×3 и уголок из трёх клеток. Слайд 10Возражение: это стрельба из пушки по воробьям!
Ответ: у нас учебные
стрельбы!
Утверждение. Всё, что решается раскрасками, решается и группами. Но не
наоборот. Задача. Решите вашу любимую «раскрасочную» задачу о невозможности замощения через группы.
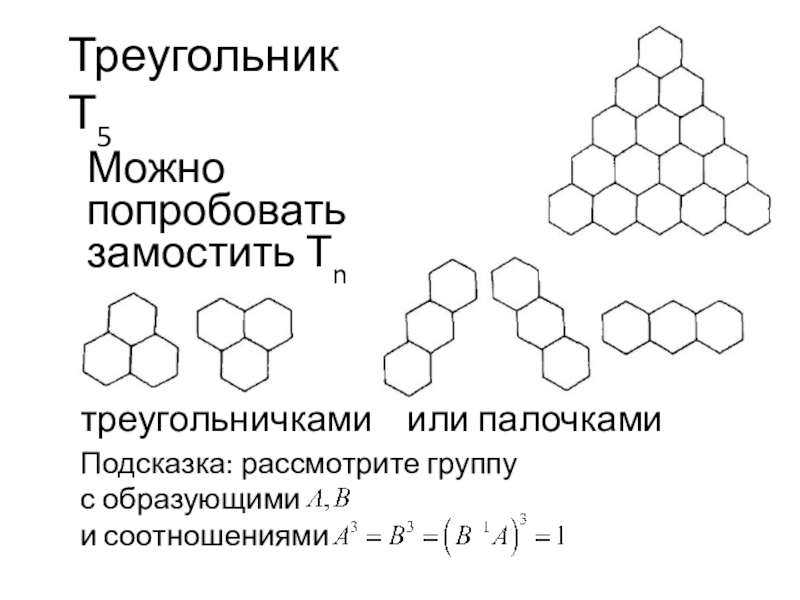
Слайд 11Треугольник Т5
Можно попробовать замостить Тn
треугольничками или палочками
Подсказка:
рассмотрите группу
с образующими
и соотношениями
Слайд 12Задача 1. Тn замощается Т2 n =
1,2,9,11 mod 12
Задача 2. Тn не замощается палочками.
Допустим, что мы
можем класть плитки из вещества или антивещества. Можно ли замостить в этом случае так, чтобы после аннигиляции каждая клетка была покрыта ровно по разу?
Задача 1’. Тn замощается Т2 (с возможным использованием антивещества) n 1 mod 3.
Задача 2’. Тn замощается палочками (с возможным использованием антивещества) n = 0 или 8 mod 9.Вывод. Не всё что делается некоммутативными группами, сделается раскраской!
Слайд 13Задача 3. Фигуру F нельзя покрыть плитками P и иx
антиплитками тогда и только тогда когда в клетках F можно
расставить числа так, чтобы сумма чисел под каждой плиткой была бы нулевой, а глобальная сумма – нет.Задача 4. Докажите, что прямоугольник 5×7 нельзя покрыть уголками из трёх клеток так чтобы каждая клетка была бы покрыта в одинаковое число слоёв.
Задача 5. Докажите, что прямоугольник m×n нельзя покрыть плитками P так, чтобы каждая клетка была
покрыта в одинаковое число слоёв, тогда и только тогда, когда можно расставить числа в клетках так, чтобы глобальная сумма была бы положительна, а сумма чисел под каждой плиткой – отрицательна.
Слайд 14Задача 6. На острове Серобуромалин живут хамелеоны: 13 серых, 15 бурых
и 17 малиновых. Если 2 хамелеона разных цветов встречаются, то
они оба меняют свой цвет на третий. Может ли случиться, что в некоторый момент все хамелеоны на острове станут одного цвета?Докажите, что для проверки возможности перехода достаточно совпадения попарных разностей количеств
хамелеонов разных цветов по модулю 3.
Задача 7. По кругу стоят 44 дерева, на каждом - по чижу.
За каждую секунду один чиж смещается по часовой
стрелке на 1, а другой - против.
Могут ли все чижи собраться на одном дереве?
Когда из одного расположения чижей можно перейти к другому?
Слайд 15Задача 8. В клетках квадратной таблицы m×m расставлены плюсы и
минусы. Известно, что в каждом подквадратике 2 на 2 стоит
четное число плюсов. Разрешается одновременно менять знак во всех клетках, расположенных в одной строке или в одном столбце. Докажите, что все знаки можно сделать плюсами.Слайд 16Задача 9. На табло стоят лампочки, каждая кнопка соединена с
некоторыми из них. Нажатие кнопки меняет состояние соединенных с ней
лампочек на противоположные. Известно, что для каждого набора лампочек найдется кнопка, соединенная с нечетным числом лампочек из данного набора. Докажите, что все лампочки можно погасить.Задача 10. На табло стоят лампочки, каждая кнопка соединена с некоторыми из них. Нажатие кнопки меняет состояние соединенных с ней лампочек на противоположные. Назовем инвариантом такой набор лампочек, что каждая кнопка, соединена с четным числом лампочек из данного набора.
Докажите, что если изначально в каждом инварианте горит четное число лампочек, то все лампочки можно погасить.
Слайд 17Задача 11. (а) Можно ли круг разрезать на несколько частей
и сложить квадрат?
(Разрезы – это прямые и дуги окружностей)
.(б) Когда одну фигуру можно перекроить в другую? (Разрезы и участки границы – это прямые и дуги окружностей) .
Задача 12. Когда один многоугольник можно параллельно перекроить в другой?
(Кусочки можно параллельно переносить, но НЕ ПОВОРАЧИВАТЬ)
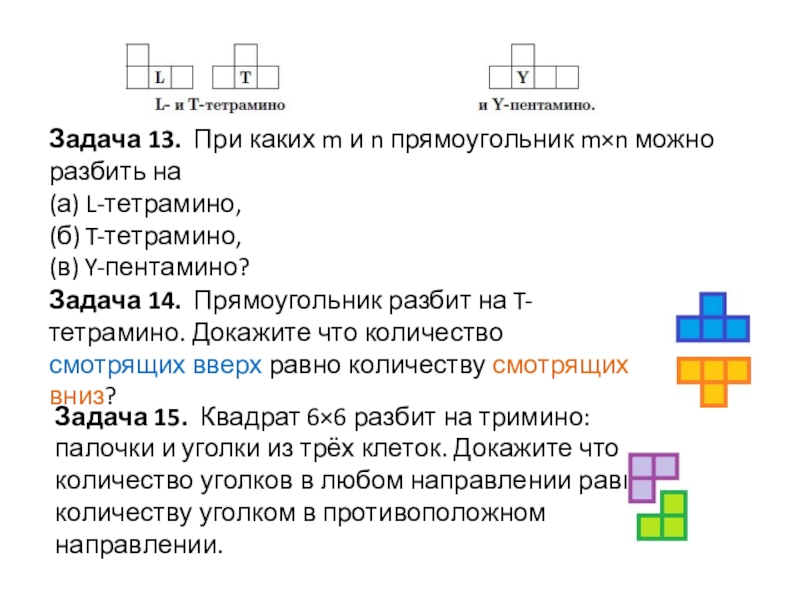
Слайд 18Задача 13. При каких m и n прямоугольник m×n можно
разбить на
(а) L-тетрамино,
(б) T-тетрамино,
(в) Y-пентамино?
Задача 14. Прямоугольник разбит на
T-тетрамино. Докажите что количество смотрящих вверх равно количеству смотрящих вниз? Задача 15. Квадрат 6×6 разбит на тримино: палочки и уголки из трёх клеток. Докажите что количество уголков в любом направлении равно количеству уголком в противоположном направлении.