Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тектоническое погружение бассейна Растяжение и термическая активизация литосферы
Содержание
- 1. Тектоническое погружение бассейна Растяжение и термическая активизация литосферы
- 2. Долгое время тектоническое погружение использовалось исключительно для
- 3. Анализ около 2000 кривых погружения поверхности фундамен-та
- 4. Продолжительность процесса растяжения литосферы(Takeshita, Yamaji 1990).Разрыв -
- 5. Параметры формирования рифтогенных бассейнов (Huismans et al.,
- 6. 2 периода тепловой реактивизации и 2
- 7. Тектоническим погружением бассейна называют смещение поверхности его
- 8. В состоянии локальной изостазии два основных процесса
- 9. Принцип вычисления вариаций амплитуды тектонического погруженияИз условия,
- 10. Равенство веса столбцов АА
- 11. Тогда вариации тектонического погружения фундамента, вызванные изменением
- 12. Существенно, что тектоническое погружение явно не зависит
- 13. Подстилающая литосфера и часть астеносферы включались в
- 14. G(0) + ρa⋅g⋅(Zk - Zt(0) - l0)
- 15. В качестве l0 выбирается нижняя граница ZM
- 16. Вариации плотностей α=3.2⋅10-5°C-1 - коэффициент термического
- 17. Распределение плотности пород фундамента с глубиной может
- 18. Фазовые переходы в мантии : (Forsyth,
- 19. Изменение плотности пород мантии с температурой и
- 20. Продолжительность и амплитуда тектонических и термических событий,
- 21. ИзостазияЛокальная изостазия литосферы бассейна (Эйри - средний
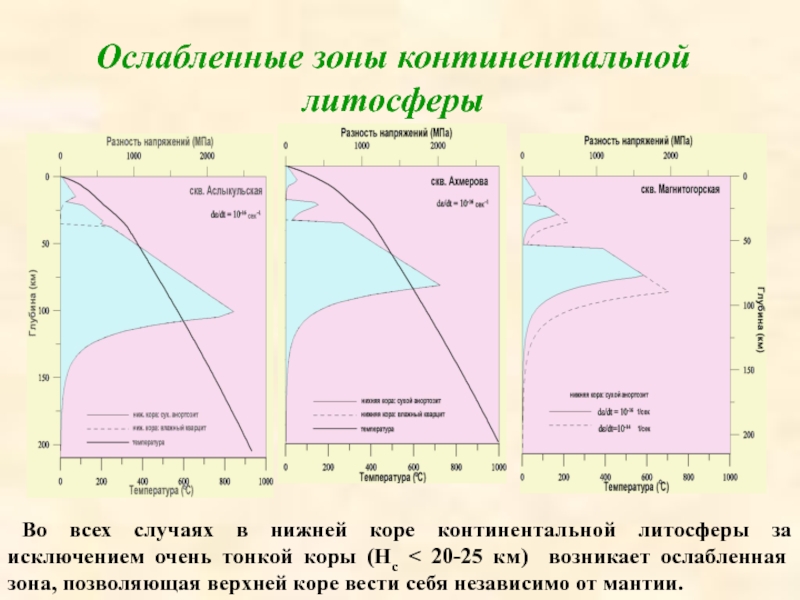
- 22. Ослабленные зоны континентальной литосферы Во всех случаях
- 23. Оценки продолжительности и амплитуд тепловых и тектонических
- 24. Тепловая активизации литосферы моделируется поднятием кровли термического
- 25. Современные примеры: все океанические и континентальные рифтовые
- 26. История погружения и термического режима осадочной толщи
- 27. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Тектоническое погружение бассейна
Растяжение и термическая активизация литосферы
Тектоническим погружением бассейна
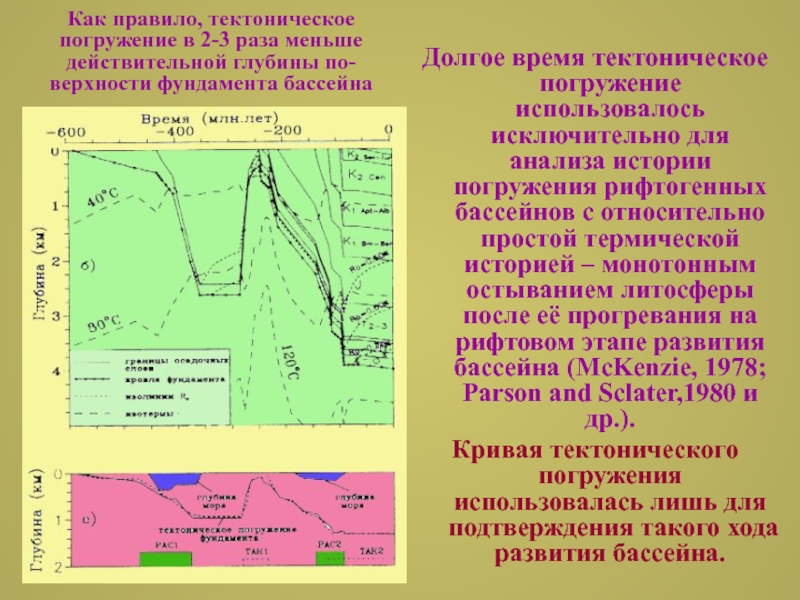
Слайд 2Долгое время тектоническое погружение использовалось исключительно для анализа истории погружения
рифтогенных бассейнов с относительно простой термической историей – монотонным остыванием
литосферы после её прогревания на рифтовом этапе развития бассейна (McKenzie, 1978; Parson and Sclater,1980 и др.).Кривая тектонического погружения использовалась лишь для подтверждения такого хода развития бассейна.
Как правило, тектоническое
погружение в 2-3 раза меньше
действительной глубины по-
верхности фундамента бассейна
Слайд 3Анализ около 2000 кривых погружения поверхности фундамен-
та свидетельствует о том,
что в истории многих бассейнов мира
этапы растяжения литосферы могли повторяться
неоднократ-но (Восточно-Баренцевоморская впадина, север норвежского
шельфа, Северное море и другие; Newman and White, 1997). Вслед за
первым событием растяжения, связанным c начальным эпизо-
зодом рифтогенеза, через 40-100 млн. лет могли следовать до-
полнительные этапы растяжения литосферы с амплитудой
1.03 - 1.3 (Huismans et al., 2001).
Имеются бассейны, в истории которых рифтовая стадия оказы-
вается промежуточной, в результате чего рифтовые грабены
оказываются наложенными на осадочные отложения предшест-
вующих стадий и погребёнными под отложениями последую-
щих формаций (верхнемеловой – миоценовый грабен Сирт в
Ливийско-Египетском бассейне, юрско-нижнемеловые грабены
Центральный и Вайкинг в Североморском бассейне; Кучерук, Ушаков, 1985).
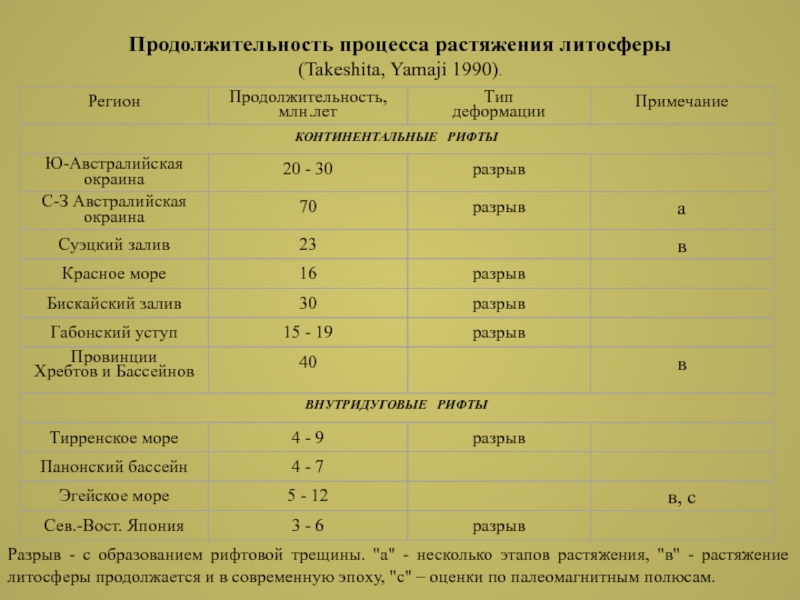
Слайд 4Продолжительность процесса растяжения литосферы
(Takeshita, Yamaji 1990).
Разрыв - с образованием рифтовой
трещины. "а" - несколько этапов растяжения, "в" - растяжение литосферы
продолжается и в современную эпоxу, "с" – оценки по палеомагнитным полюсам.Слайд 5Параметры формирования рифтогенных бассейнов (Huismans et al., 2001)
β -
утонение коры; δ - утонение подкоровой литосферы; t1 – время
первой рифтовой фазы; t2 – время второй рифтовой фазы; t3 – время известково-щелочного вулканизма; t4 – время щелочного вулканизма; t1 – время пострифтового сводообразования.Слайд 6
2 периода тепловой реактивизации и 2 периода растяжения в
истории погружения бассейна Уэд эль-Миа, восточный Алжир
Слайд 7Тектоническим погружением бассейна называют смещение поверхности его фундамента за вычетом
влияния нагрузки воды и осадков
Таким образом, моделирование бассейнов должно
включать механизм, учитывающий неоднократные периоды тепловой реактивизации и растяжения его литосферы. Анализ тектонического погружения бассейна позволяет оценивать амплитуду и продолжительность этих событий.Слайд 8В состоянии локальной изостазии
два основных процесса определяют глубину
поверхности фундамента
бассейна:
нагрузка осадков и воды на поверхность фундамента (амплитуда смещения
поверхности ZTs,) и изменение в распределениии плотности пород фундамента с глубиной (амплитуда смещения поверхности ZTb) (например, при нагревании, охлаждении и растяжении литосферы, смещении фазовых границ, преобразовании габбро в эклогит в основании коры и др.)
Т.е. в отсутствии этих процессов глубина поверхности фундамента оставалась бы неизменной
Слайд 9Принцип вычисления вариаций амплитуды тектонического погружения
Из условия, что веса всех
столбцов уравновешиваются на уровне компенсации (нижняя граница области счёта Zk),
получаются уравнения для расчёта вариаций составляющих тектонического погружения ZTs и ZTb.Слайд 10
Равенство веса столбцов АА и А1А1 приводит
к уравнению:
g⋅ρw⋅Zw(0) + G(0) + g⋅ρa⋅(Zk - Zw(0) -
l0) = G(0) + g⋅ρa⋅(Zk - Zt(0) - l0)
из которого следует:
В то же время из равенства веса столбцов ВВ и В1В1:
g⋅ρw⋅Zw(t) + G(t) + g⋅ρs⋅S(t) + g⋅ρa⋅(Zk - Zw(t) - S(t) - l0) =
= G(t) + g⋅ρa⋅(Zk - Zt(t) - l0)
следует:
Из (7) и (8) выводим формулу, определяющую относительн
Слайд 11Тогда вариации тектонического погружения фундамента, вызванные изменением поверхностной нагрузки, можно
выразить формулой:
Здесь t - время, t = 0
- начало формирования бассейна, Zw(t) - палеоглубины водной колонки на время t, S(t) - толщина осадочного покрова, ρa и ρw - плотности астеносферы и воды. Средняя плотность пород в столбце осадков ρs(t)::
Слайд 12Существенно, что тектоническое погружение явно не зависит от эвстатических колебаний
уровня мирового океана
Эвстатические колебания могли быть вызваны широкомасштабным
таянием ледников, глобальными изменениями в картине спрединга, вытеснением воды при эрозии континентов, осушением или заполнением большиx водныx бассейнов Используя три наиболее известныx эвстатических кривых можно получить различие в оценкаx уровня океана в 100 - 250 м (Su et al. 1989) и эти вариации при умеренныx скоростях осадконакопления могут затушёвывать эффект тектоническиx событий на реконструируемое положение поверxности фундамента. (Артюшков и др., 1998) - многие из быстрых флюктуаций глубины морских бассейнов на континентальной коре были обусловленными не эвстатическими колебаниями уровня мирового океана, а проявлением в отдельные эпохи относительно быстрых вертикальных тектонических движений коры с амплитудами 20-100 м.
Слайд 13Подстилающая литосфера и часть астеносферы включались в область расчёта температуры
наряду с осадочной толщей. И это позволяло вычислять амплитуду тектонического
погружения, ZTb, из анализа изменений в глубинном распределении плотностей в фундаментеВыражение для ZTb получаем, приравнивая веса столбцов
А1А и В1В1 на правом рисунке:
Слайд 14G(0) + ρa⋅g⋅(Zk - Zt(0) - l0) = = G(t)
+ ρa⋅g⋅(Zk - Zt(t) - l0)
Из равенства веса столбцов А1АI
и В1В1 имеем:g - ускорение силы тяжести и G - вес столбца фундамента некоторой фиксированной высоты lo:
Глубина изостатической компенсации приходится на реоло-гически слабые породы астеносферы или низов литосферы.
Распределение плотности пород фундамента определяет ZTb.
Слайд 15В качестве l0 выбирается нижняя граница ZM области счёта температуры
в начальный момент развития бассейна (t = 0).
При этом толщина
столбца фундамента (l0) остаётся неизменной во всё время моделирования бассейна, наращиваясь в периоды растяжения литосферы, в то время как ZM - нижняя граница области счёта температуры – может меняться на толщину отложенных или эродированных осадков. В такой модели глубина изостатической компенсации лежит ниже или совпадает с максимальной глубиной ZM в процессе моделирования бассейна. Такая глубина изостатической компенсации приходится на реологически слабые породы астеносферы или низов литосферы.
Распределение плотности пород фундамента определяет ZTb.
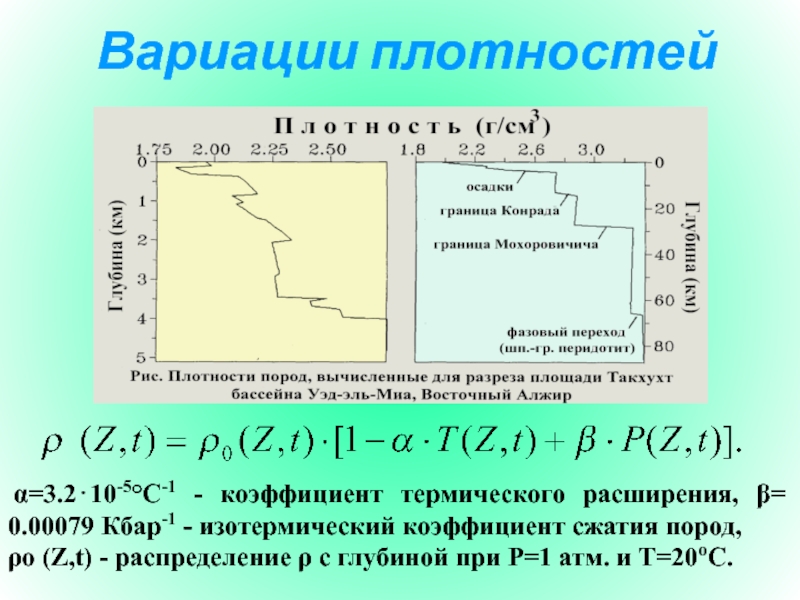
Слайд 16Вариации плотностей
α=3.2⋅10-5°C-1 - коэффициент термического расширения, β= 0.00079
Кбар-1 - изотермический коэффициент сжатия пород,
ρo (Z,t) - распределение
ρ с глубиной при P=1 атм. и T=20oC. Слайд 17
Распределение плотности пород фундамента с глубиной может изменяться :
а) переходе от “гранитного” слоя коры к
“базальтовому” и затем к мантии,б) при фазовых переходах в мантии
в) при изменении мощности коры в периоды
растяжения литосферы или эрозии коры снизу.
Слайд 18
Фазовые переходы в мантии :
(Forsyth, Press 1971; Wood,
Yuen, 1983; Yamasaki, Nakada, 1997)
Плакиоглазовый перидотит в шпинелевый
(ρо=3.26→ 3.30 г/см3)
P(кбар) = 0.00515 × T(°C) + 3.92
Шпинелевый перидотит в гранатовый
(ρо=3.30→ 3.38 г/см3)
P(Кбар) = 0.000025×[ Т(°С) - 900 ]2 + 15
Первый переход приходится на глубины от 12 до 32 км
и в континентальной литосфере не имеет места, так как приходится на кору.
Второй переход – на глубины от 40 до 70 км. Он объясняет от 200 до 400 м рельефа поверxности фундамента.
Слайд 19Изменение плотности пород мантии с температурой и давлением
Для Р=30 кбар
(z=93 км) и Т=1000°С получим Δρ = 0.078 – 0.106
= - 0.028 г/см3. При Р=50 кбар (z=154 км) и Т=1200°С - Δρ ≈0. Таким образом, температурный вклад в плотность пород в мантии будет преобладать на глубинах z < 100 км, а вклад давления - при z > 200 км.Слайд 20Продолжительность и амплитуда тектонических и термических событий, имевших место в
истории развития литосферы бассейна, оцениваются из условия совпадения двух кривых
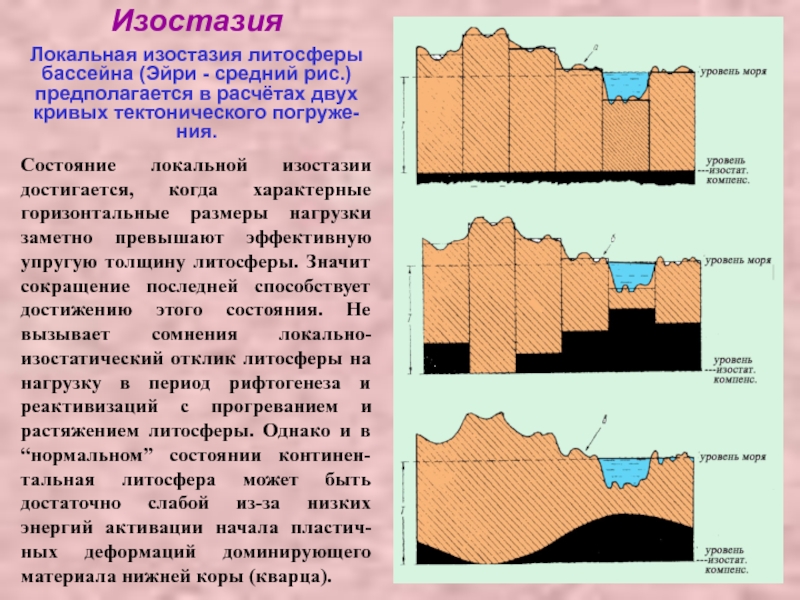
тектонического погружения – рассчитанной удалением нагрузки воды и осадков и по изменениям плотности пород фундаментаСлайд 21Изостазия
Локальная изостазия литосферы бассейна (Эйри - средний рис.) предполагается в
расчётах двух кривых тектонического погруже-ния.
Состояние локальной изостазии достигается, когда
характерные горизонтальные размеры нагрузки заметно превышают эффективную упругую толщину литосферы. Значит сокращение последней способствует достижению этого состояния. Не вызывает сомнения локально-изостатический отклик литосферы на нагрузку в период рифтогенеза и реактивизаций с прогреванием и растяжением литосферы. Однако и в “нормальном” состоянии континен-тальная литосфера может быть достаточно слабой из-за низких энергий активации начала пластич-ных деформаций доминирующего материала нижней коры (кварца). Слайд 22Ослабленные зоны континентальной литосферы
Во всех случаях в нижней
коре континентальной литосферы за исключением очень тонкой коры (Hc
20-25 км) возникает ослабленная зона, позволяющая верхней коре вести себя независимо от мантии.Слайд 23Оценки продолжительности и амплитуд тепловых и тектонических активизаций бассейнов из
анализа тектонических кривых бассейна
Растяжение литосферы (или эрозия коры снизу)
модели-руется в виде последователь-ности слабых эпизодов растя-жений с амплитудами Δβi , от-вечающиx каждый своему ин-тервалу времени Δti, так что полная амплитуда растяжения за время Δt = Δt1 + Δt2 + ⋅⋅⋅ +Δtn достигала β= Δβ1 ⋅Δβ2 ⋅⋅⋅Δβn. Как правило, Δt (раст.) > 20-100 млн.лет и тогда V(раст) ≤ 0.1 мм/год – термический нагрев незначителен (слайд 14). Но для Баренцева моря (β=2.12) нагрев при растяжении заметен.
Слайд 24
Тепловая активизации литосферы моделируется поднятием кровли термического диапира с температурой
1000-1200oC. При этом распределение температур в литосфере ниже кровли диапира
переписывается на каждом шаге времени на распределение температур, линейно возрастающее от температуры кровли диапира до значения TМ, поддерживаемое в основании области счета. Кровля диапира поднималается со скоростью 0.5 до 5 км/млн.лет в течение 5 - 50 млн.лет и затем поддерживается на той же глубине, либо частично релаксирует.Пример: бассейн Уэд эль-Миа, пл. Такхухт. 1-ая тепловая активизация: кровля астеносферного диапира (1000°C) поднима-ется со скоростью 5.5 км/млн.лет от 280 до 270 млн. лет назад и держится на неизменной глубине (q=100 мВт/м2) следующие 35 млн.лет. 2-ая тепловая активизация: подьём кровли диапира со скоростью 1 км/млн.лет со 120 по 100 млн.лет и стагнация с эффективным тепловым потоком на поверхности около 60 мВт/м2 по настоящее время.
Слайд 25
Современные примеры:
все океанические и континентальные рифтовые зоны, Афар и
др.
Пример тепловой активизации и растяжения в кайноззое - бассейн
Иллизи в Восточном Алжире. Высокие температуры, измеренные в современном разрезе (около 110°С на глубине 2 км) предполагают термическую активизацию в кайно-зое, а низкий рельеф бассейна - одновременное растяжение бассейна с амплитудой β≈1.16 (из совпадения тектонических кривых). Одновременное действие тепловой активизации и растяжения литосферы
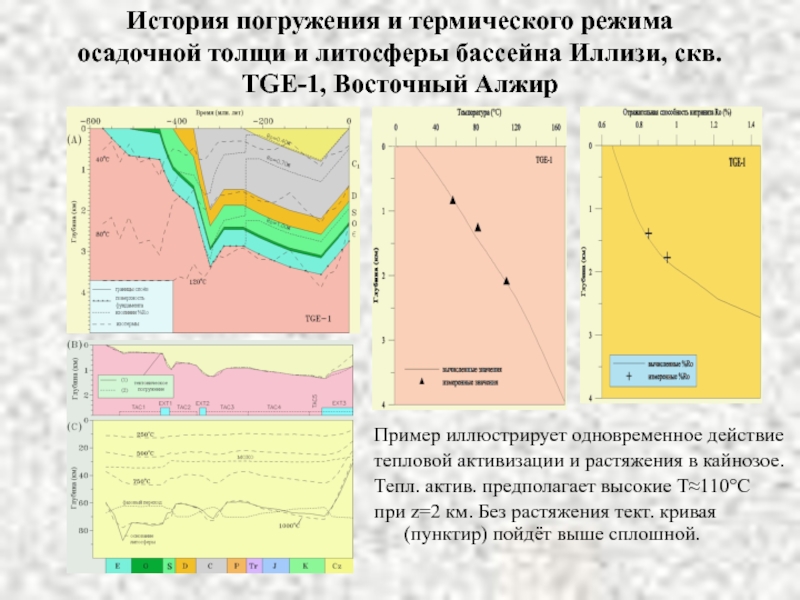
Слайд 26История погружения и термического режима осадочной толщи и литосферы бассейна
Иллизи, скв. TGE-1, Восточный Алжир
ааааа
Пример иллюстрирует одновременное действие
тепловой активизации
и растяжения в кайнозое.Тепл. актив. предполагает высокие Т≈110°С
при z=2 км. Без растяжения тект. кривая (пунктир) пойдёт выше сплошной.