Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема 2. Обработка результатов измерений
Содержание
- 1. Тема 2. Обработка результатов измерений
- 2. Статистическая обработка результатов измерений – обработка результатов
- 3. Доверительная вероятность и доверительный интервал
- 4. Прямые измерения с многократными независимыми и
- 5. Алгоритм обработки результатов измеренийИсключение систематических погрешностей;
- 6. Исключение систематических погрешностей устранение источников погрешностей – правильный
- 7. Классификация систематических погрешностей:постоянныепеременные:монотонно изменяющиеся;периодические;прогрессирующие
- 8. Методы исключения (уменьшения) систематических погрешностейметод замещения;метод компенсации
- 9. 2) Оценка результата измерения и его среднеквадратического
- 10. 2) Оценка результата измерения и его среднего квадратического отклоненияЗная оценку истинного значения величины xи:
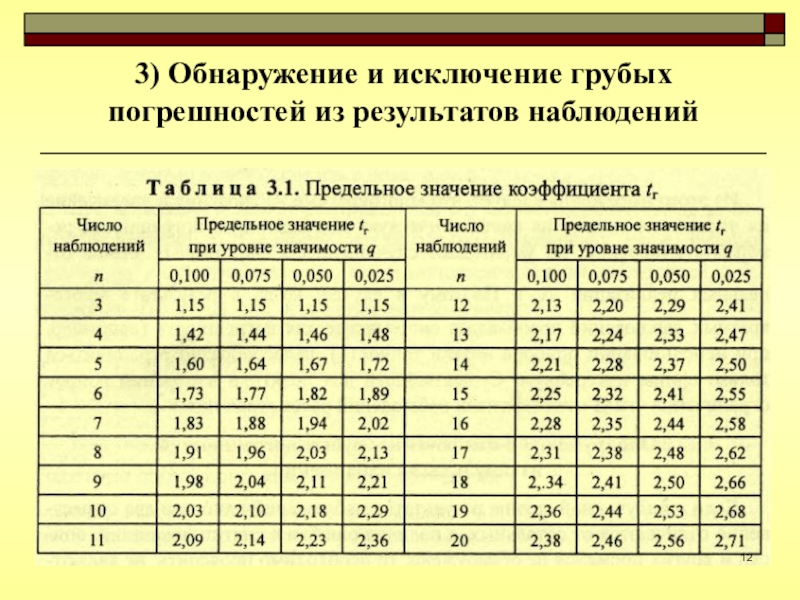
- 11. 3) Обнаружение и исключение грубых погрешностей из
- 12. 3) Обнаружение и исключение грубых погрешностей из результатов наблюдений
- 13. 3) Обнаружение и исключение грубых погрешностей из
- 14. 4) Оценка результата измерения и среднего
- 15. 5) Определение границ доверительного интервала Оценка измеряемой
- 16. 5) Определение границ доверительного интервала В зависимости
- 17. Условия применения:объем априорной информации об объекте такой,
- 18. Прямые однократные измерения Погрешность результата прямого однократного
- 19. 2.5. Обработка результатов однократных измерений2.5.2. Косвенные измеренияКосвенные измерения
- 20. Оценка СКО случайной погрешности результата косвенного измерения
- 21. 2.5. Обработка результатов однократных измерений2.5.3. Совместные измерения
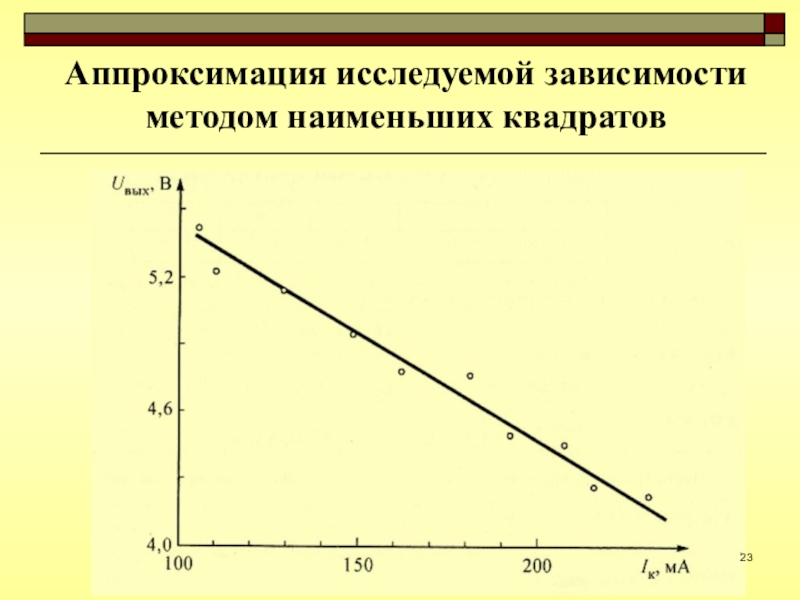
- 22. Метод наименьших квадратовСущность метода наименьших квадратов:наивероятнейшими значениями
- 23. Аппроксимация исследуемой зависимости методом наименьших квадратов
- 24. Вывод:Статистическая обработка результатов измерения повышает точность измерений.
- 25. Скачать презентанцию
Статистическая обработка результатов измерений – обработка результатов измерений с целью получения достоверных данныхГлавная задача любых измерений – получение с заданной точностью и достоверностью количественной информации о значениях физических величин, свойствах физических
Слайды и текст этой презентации
Слайд 1Тема 2.
Обработка результатов измерений
2.4. Статистическая обработка результатов измерений (многократные равноточные
наблюдения)
Слайд 2Статистическая обработка результатов измерений – обработка результатов измерений с целью
получения достоверных данных
Главная задача любых измерений –
получение с заданной
точностью и достоверностью количественной информациио значениях физических величин,
свойствах физических объектов,
закономерностях процессов
Практическая задача статистической обработки – оценка измеряемой величины и определение доверительного интервала, в котором находится ее истинное значение
Слайд 4Прямые измерения
с многократными независимыми и равноточными наблюдениями
Способ
статистической обработки
основан на гипотезе
о распределении случайных погрешностей
по
нормальному закону Равноточными называются измерения,
проводимые одним экспериментатором
в одинаковых условиях
и с помощью одного средства измерений
Слайд 5Алгоритм обработки
результатов измерений
Исключение систематических погрешностей;
Оценка результата измерения и
его среднеквадратического отклонения;
Обнаружение и исключение грубых погрешностей из результатов наблюдений;
Исправление
оценки результата измерения и среднего квадратического отклонения;Определение границ доверительного интервала при заданной доверительной вероятности
Слайд 6Исключение систематических погрешностей
устранение источников погрешностей –
правильный выбор метода и
средства измерения
определение поправок
оценка границ неисключенных систематических
погрешностей
Можно исключить, уменьшить
или учесть влияние систематических погрешностей, но сначала – надо обнаружить.
1)
Слайд 7Классификация систематических погрешностей:
постоянные
переменные:
монотонно изменяющиеся;
периодические;
прогрессирующие
Слайд 8Методы исключения (уменьшения) систематических погрешностей
метод замещения;
метод компенсации погрешности по знаку;
метод
противопоставления;
метод рандомизации;
метод введения поправок;
метод симметричных наблюдений;
метод анализа знаков;
графический метод
Слайд 92) Оценка результата измерения и
его среднеквадратического отклонения
При нормальном законе
распределения
случайной погрешностей за истинную величину
принимают ее оптимальную оценку,
равную оценке математического ожиданияряда наблюдений, то есть полагают,
что эта величина – результат измерения
Слайд 102) Оценка результата измерения
и его среднего квадратического отклонения
Зная оценку
истинного значения величины xи:
Слайд 113) Обнаружение и исключение грубых погрешностей из результатов наблюдений
Результаты группы
измерений упорядочивают по возрастанию
Вычисляют оценку среднеарифметического значения и среднеквадратического отклонения
этой выборки Проводят расчет коэффициентов tn для предполагаемых промахов
Слайд 133) Обнаружение и исключение грубых погрешностей из результатов наблюдений
4. Критерий
«трех сигм» применяется для результатов измерений, распределенных по нормальному закону:
считаем, что результат, полученный с вероятностью q ˂0,003, маловероятен и его можно считать промахом, еслиДанный критерий хорошо работает при числе измерений больше 20…50.
_______________________________________
Далее проверяют гипотезу о нормальном распределении результатов наблюдений.
Слайд 144) Оценка результата измерения и среднего квадратического отклонения по исправленному ряду
наблюдений
Далее следует пересчитать оценку среднеарифметического значения и среднеквадратического отклонения этой
выборки, исключив промахи.
Слайд 155) Определение границ доверительного интервала
Оценка измеряемой величины является случайной
величиной, и следовательно отличается от нее на некоторую абсолютную погрешность.
Чаще всего определяют симметричный доверительный интервалинтервал.
При технических измерениях доверительная погрешность принимается равной 0,95.
Слайд 165) Определение границ доверительного интервала
В зависимости от числа измерений
применяют либо нормальный закон распределения либо распределение Стьюдента.
Используя таблицы по
заданной доверительной вероятности определяют соответствующий коэффициент t(Pд,n)Определяют границу случайной погрешности результата измерения,
а также границы доверительного интервала
Слайд 17Условия применения:
объем априорной информации об объекте такой, что аналитическая модель
объекта и определение измеряемой величины не вызывают сомнений;
метод измерений достаточно
изучен и его погрешности либо заранее устранены, либо оценены;средства измерения исправны, а их метрологические характеристики соответствуют установленным нормам
Результат прямого однократного измерения физической величины – показание снятое с используемого средства измерения.
2.5. Обработка результатов однократных измерений
2.5.1. Прямые однократные измерения
Слайд 18Прямые однократные измерения
Погрешность результата прямого однократного измерения включает:
погрешность средства
измерения (инструментальную погрешность);
методическую погрешность;
субъективную (личную) погрешность оператора
Каждая из этих составляющих
может иметь неисключенные систематические составляющие и случайные.
Слайд 192.5. Обработка результатов однократных измерений
2.5.2. Косвенные измерения
Косвенные измерения - искомую величину
определяют на основании известной зависимости между этой величиной и величинами,
получаемыми в результате прямых измерений.Эти измеренные значения – аргументы некоторой функции.
Результат косвенного измерения вычисляется при подстановке в зависимость оценок аргументов.
Слайд 22Метод наименьших квадратов
Сущность метода наименьших квадратов:
наивероятнейшими значениями аргументов искомой аналитической
зависимости будут такие, при которых сумма квадратов отклонений экспериментальных значений
функции y, будет наименьшей
