Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема 7 Синтез многовыходных ЛС
Содержание
- 1. Тема 7 Синтез многовыходных ЛС
- 2. Постановка задачи синтеза ЛС по сложным ЛФНа
- 3. Ситуация 1Пример 1. Заданы две логические функции,
- 4. Пример 1 продолжениеМожно заметить, что в схемах
- 5. Ситуация 2Если функции Y1 и Y2 заданы
- 6. Ситуация 3Если множества обеих реализуемых функций не
- 7. Логическая схема полусумматораВОПРОС. МОЖНО ЛИ СХЕМУ УПРОСТИТЬ?
- 8. Логическая схема полусумматораДа, предыдущую логическую схему можно упростить если в функции суммы использовать значение переноса (ПРОВЕРИТЬ!!!).
- 9. ЗадачаРазработайте логическую функцию и логическую схему полного одноразрядного сумматора.СумматорABP-1SPДля решения задачи используйте таблицу состояний и СНДФ
- 10. РЕШЕНИЕ ЗАДАЧИСДНФ суммыСДНФ переносаминимизацияМожно создать сумматор любой разрядностиВОПРОС. ВОЗМОЖНО УПРОСТИТЬ ЛС?
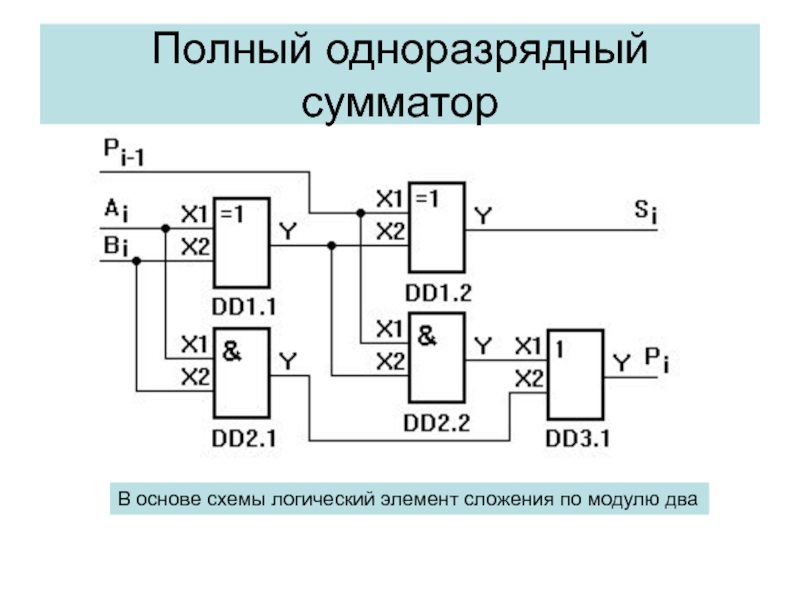
- 11. Полный одноразрядный сумматорВ основе схемы логический элемент сложения по модулю два
- 12. Логическая схема с тремя выходамиПусть даны логические
- 13. Решение задачи11&&&11
- 14. Логическая схема матричного умножителяКонъюнкторыСумматорПроцесс умножения кода А
- 15. Введение в теорию цифровых автоматовПредметом теории автоматов
- 16. Задача анализаПо заданному автомату описать его поведение.
- 17. Задача синтезаПостроить автомат с наперед заданным поведением
- 18. Задача полнотыПусть M – некоторое множество автоматов.
- 19. Задача минимизацииПостроить автомат, минимальный заданному. Минимальный автомат
- 20. Классификация абстрактных автоматов автоматовПолностьюопределенныеЧастичноопределенныеВероятностныеДетерминированныеУстойчивыеНеустойчивые1 уровень2 уровень3 уровень
- 21. По определенности функцийПолностью определенный автомат имеет для каждого состояния входа определенное внутреннее состояние
- 22. По однозначности функции переходаВ детерминированных автоматах под
- 23. По устойчивости состоянийПереход в другое состояние возможен
- 24. Понятие цифрового автомата терминологияЦифровой автомат – цифровое
- 25. Любой цифровой преобразователь информации можно представить в
- 26. Особенности цифрового автоматаАвтомат имеет конечное множество внутренних
- 27. Задание алгоритма работы автоматаМножество букв входного алфавита
- 28. Задание алгоритма работы автомата через функцию переходаФункция
- 29. Задание алгоритма работы автомата через функцию выходаФункция
- 30. Автомат МилиЕсли выходной сигнал зависит не только
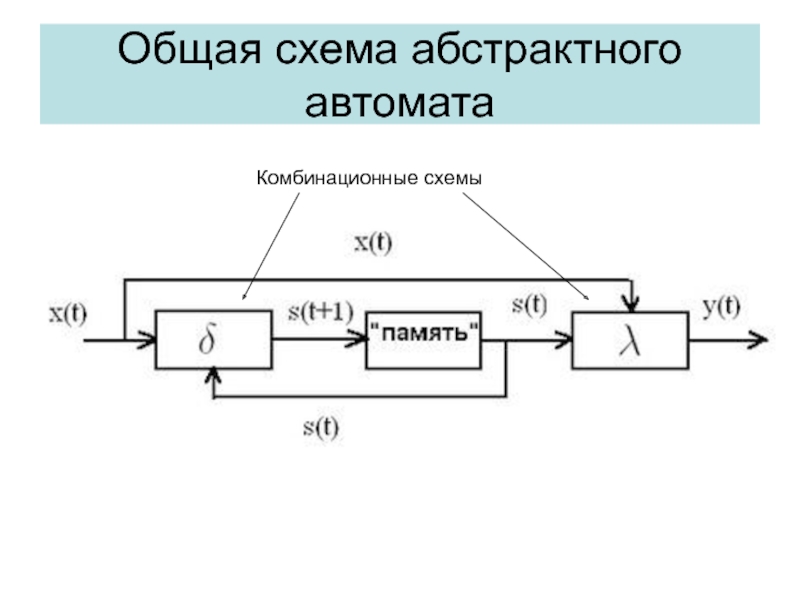
- 31. Общая схема абстрактного автоматаКомбинационные схемы
- 32. ПРИМЕР задания автомата МилиЗадание автомата Мили табличным
- 33. Пример задания автомата МураВ автомате Мура выходной
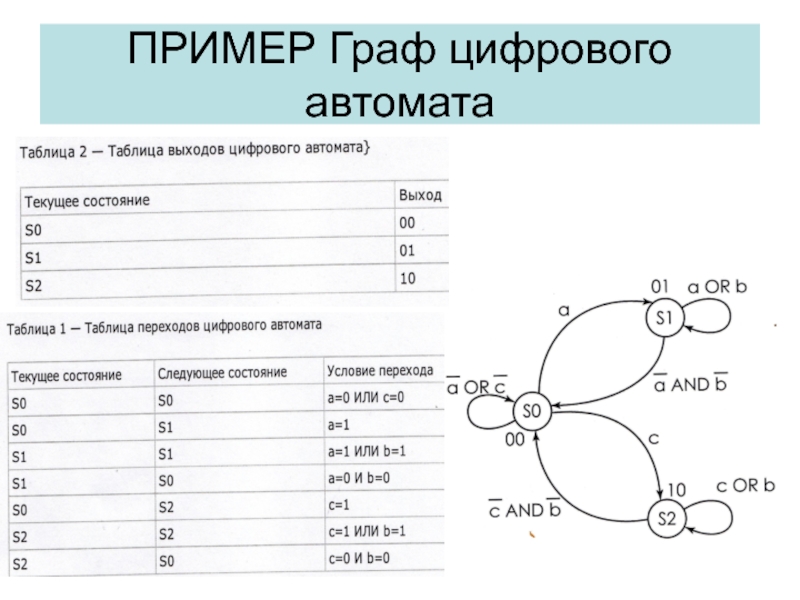
- 34. ПРИМЕР Граф цифрового автомата
- 35. Схема цифрового автоматаПри реализации схемы цифрового автомата
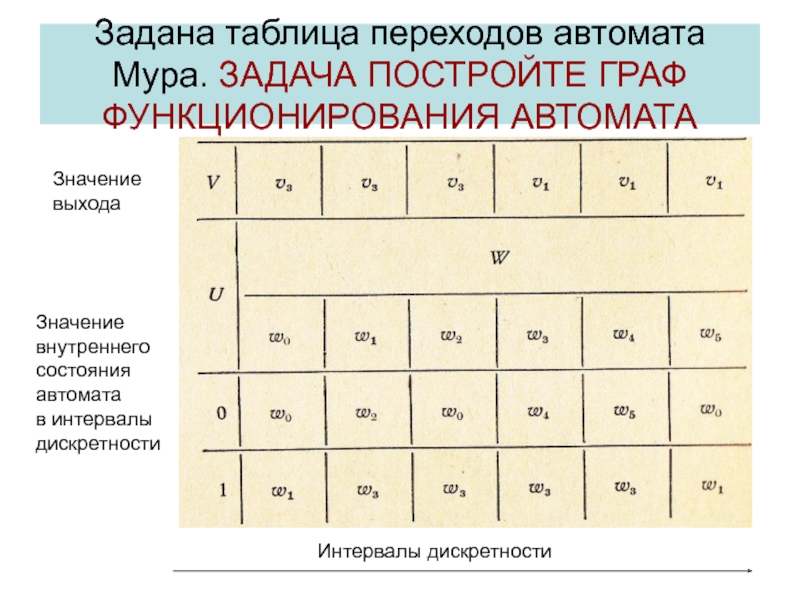
- 36. Задана таблица переходов автомата Мура. ЗАДАЧА ПОСТРОЙТЕ ГРАФ ФУНКЦИОНИРОВАНИЯ АВТОМАТАЗначение выходаЗначение внутреннегосостоянияавтоматав интервалыдискретностиИнтервалы дискретности
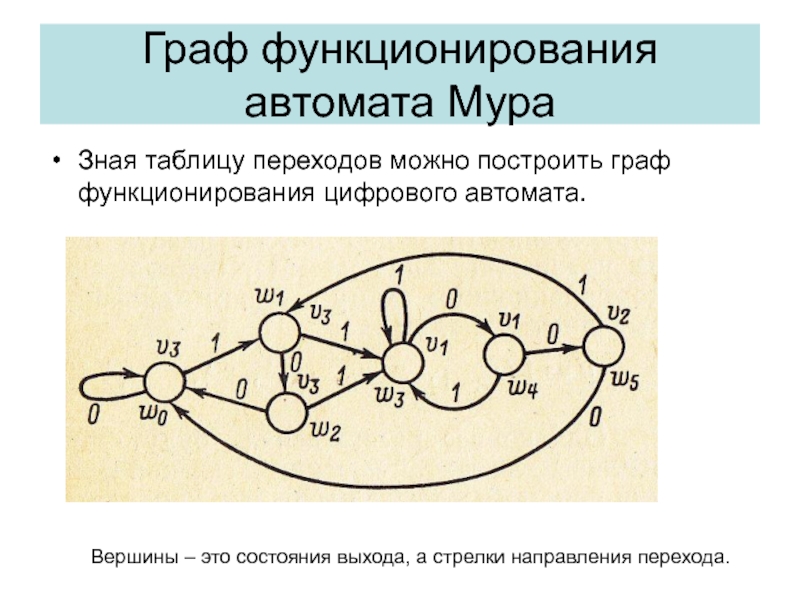
- 37. Граф функционирования автомата МураЗная таблицу переходов можно
- 38. Применение понятия цифрового автоматаПример кодирования в двоичном алфавите десятичной системы счисления
- 39. Синхронные и асинхронные автоматыАвтомат называется асинхронным, если
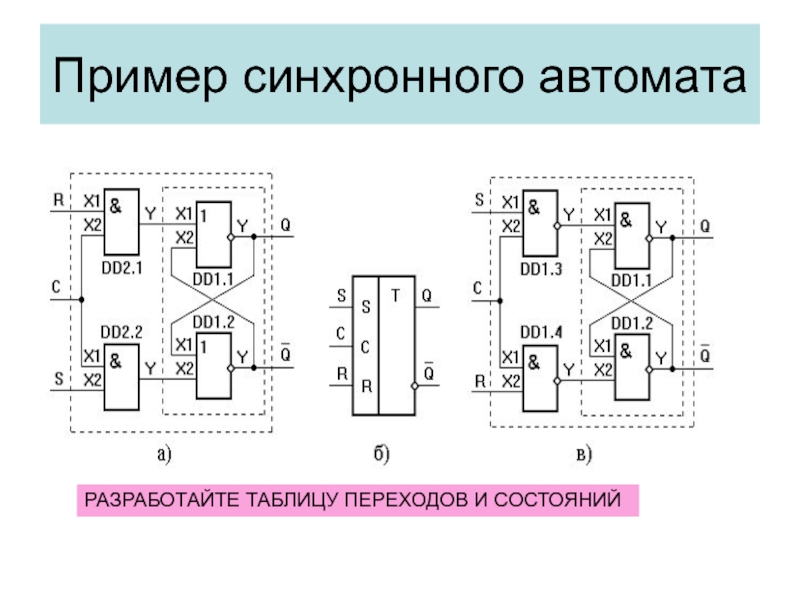
- 40. Пример синхронного автоматаРАЗРАБОТАЙТЕ ТАБЛИЦУ ПЕРЕХОДОВ И СОСТОЯНИЙ
- 41. Скачать презентанцию
Постановка задачи синтеза ЛС по сложным ЛФНа практике редко встречаются логические схемы с одним выходом, реализующие одну логическую функцию.Обычно схемы имеют несколько выходов, причем значение ЛФ на всех выходах зависят от
Слайды и текст этой презентации
Слайд 1Тема 7 Синтез многовыходных ЛС
Цель: рассмотреть варианты синтеза многовыходных логических
схем; понятие цифрового автомата.
Слайд 2Постановка задачи синтеза ЛС по сложным ЛФ
На практике редко встречаются
логические схемы с одним выходом, реализующие одну логическую функцию.
Обычно схемы
имеют несколько выходов, причем значение ЛФ на всех выходах зависят от одного набора переменных. Например – дешифратор.Задача усложняется, если применяются элементы памяти.
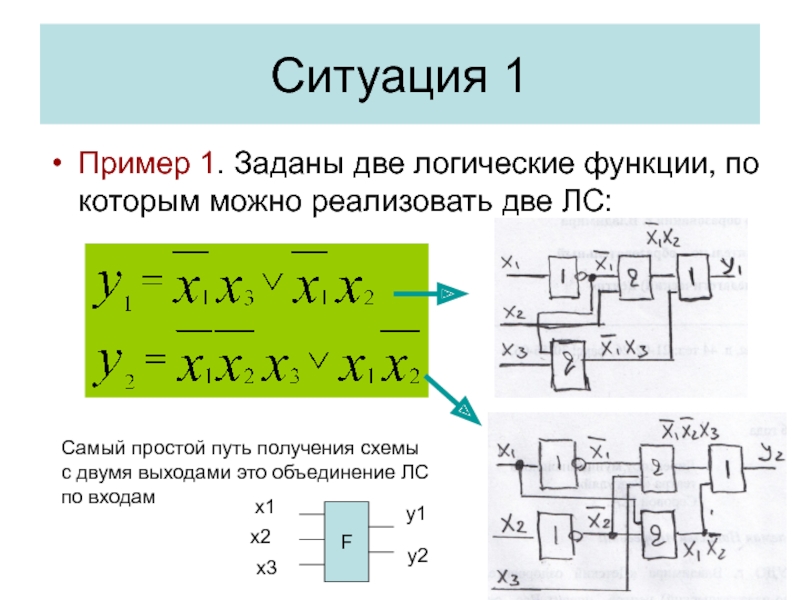
Слайд 3Ситуация 1
Пример 1. Заданы две логические функции, по которым можно
реализовать две ЛС:
Самый простой путь получения схемы
с двумя выходами
это объединение ЛСпо входам
F
y1
y2
x1
x2
x3
Слайд 4Пример 1 продолжение
Можно заметить, что в схемах есть общий инвертор.
При объединении это можно учесть. НО ДЛЯ РЕАЛИЗАЦИИ НЕОБХОДИМО 8
ЭЛЕМЕНТОВ!!!Но если применить алгебраический прием
То можно получить ЛС состоящую из семи элементов. РЕШИТЬ!!!
Слайд 5Ситуация 2
Если функции Y1 и Y2 заданы множествами и одно
из них содержится в другом, то одну из этих функций
можно выразить через другую, используя дополнительную подфункцию.Пусть заданы функции:
НЕОБХОДИМО ОПРЕДЕЛИТЬ ЛС ВЕРНА?
Слайд 6Ситуация 3
Если множества обеих реализуемых функций не пересекаются, т.е. множество
одной функции содержится во множестве другой.
В качестве примера рассмотрим функции
одноразрядного полусумматора:Одноразрядный
полусумматор
а
b
s
p
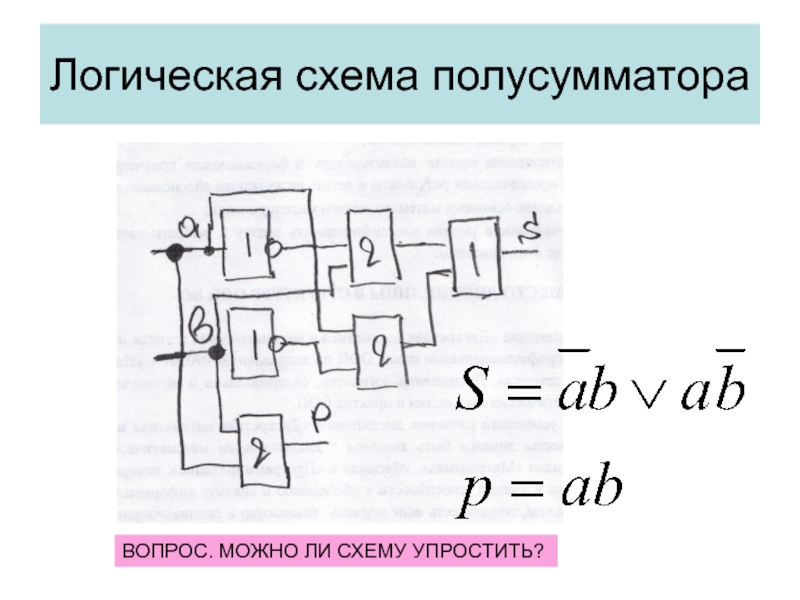
Постойте логическую схему одноразрядного полусумматора
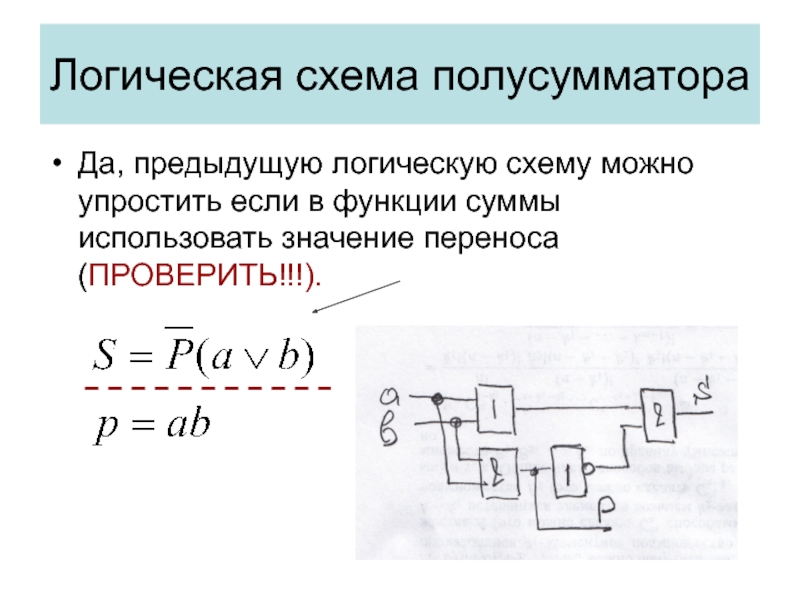
Слайд 8Логическая схема полусумматора
Да, предыдущую логическую схему можно упростить если в
функции суммы использовать значение переноса (ПРОВЕРИТЬ!!!).
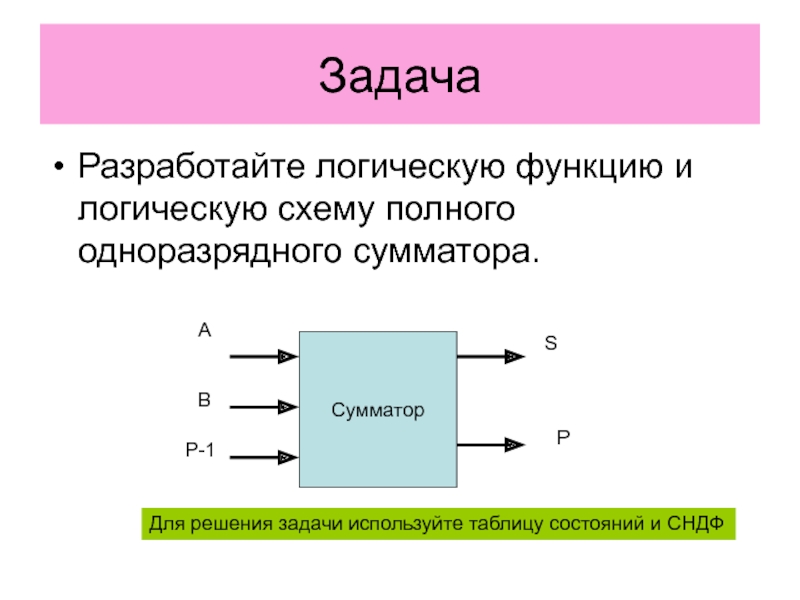
Слайд 9Задача
Разработайте логическую функцию и логическую схему полного одноразрядного сумматора.
Сумматор
A
B
P-1
S
P
Для решения
задачи используйте таблицу состояний и СНДФ
Слайд 10РЕШЕНИЕ ЗАДАЧИ
СДНФ суммы
СДНФ переноса
минимизация
Можно создать сумматор любой разрядности
ВОПРОС. ВОЗМОЖНО УПРОСТИТЬ
ЛС?
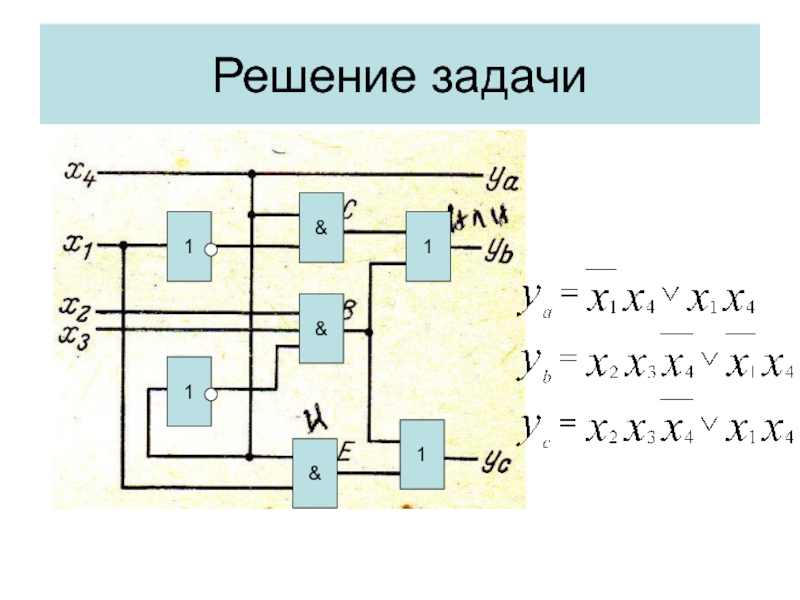
Слайд 12Логическая схема с тремя выходами
Пусть даны логические функции:
С
E
B
E
С
B
Создание общей логической
схемы будет начинаться с создания
логических схем для логических функций С.Е.В
Найдем
общие минтермы
Слайд 14Логическая схема матричного умножителя
Конъюнкторы
Сумматор
Процесс умножения кода А на код В
можно представить схемой:
ЗАДАЧА. ПОСТРОИТЬ ЛОГИЧЕСКУЮ СХЕМУ ДВУХ РАЗРЯДНОГО
УМНОЖИТЕЛЯ
Слайд 15Введение в теорию цифровых автоматов
Предметом теории автоматов является изучение математических
моделей преобразователей дискретной информации. В данной теории решаются следующие основные
задачи: анализ и синтез автоматов, определение полноты, минимизация и эквивалентные преобразования автоматов. Дадим краткую формулировку каждой из перечисленных задач.
Слайд 16Задача анализа
По заданному автомату описать его поведение. Вариант постановки: по
неполному описанию автомата установить некоторые его свойства.
Слайд 17Задача синтеза
Построить автомат с наперед заданным поведением (алгоритмом функционирования). Задачу
синтеза принято рассматривать двояко: абстрактный синтез как построение математической модели
автомата и структурный синтез как разработку функциональной логической схемы автомата.
Слайд 18Задача полноты
Пусть M – некоторое множество автоматов. Определить, обладает ли
совокупность автоматов, составляющих подмножество M’ множества M, свойством полноты. Иными
словами, если ко всем автоматам подмножества M’ конечное число раз применить операцию суперпозиции, совпадут ли M’ и M?
Слайд 19Задача минимизации
Построить автомат, минимальный заданному. Минимальный автомат обладает наименьшим числом
компонентов модели (в частности, минимальной мощностью множества так называемых состояний)
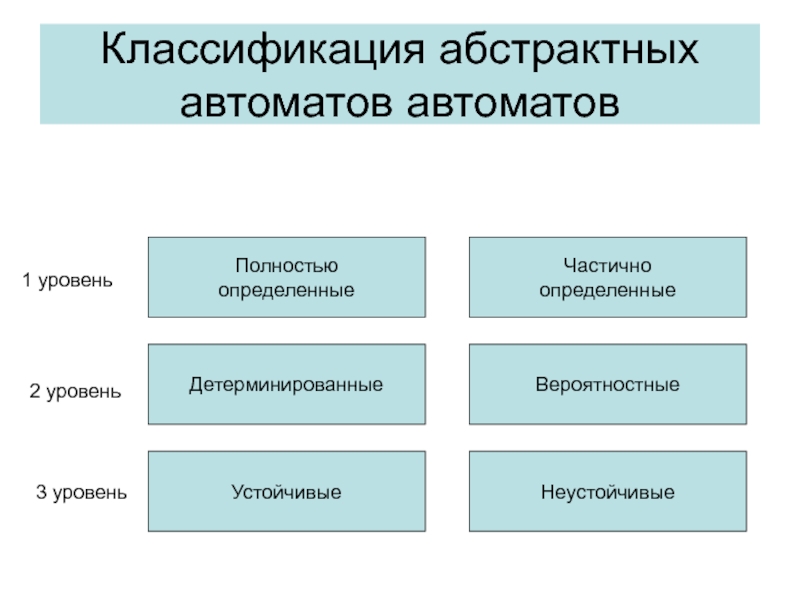
и при этом функционально эквивалентен заданному автомату.
Слайд 20Классификация абстрактных автоматов автоматов
Полностью
определенные
Частично
определенные
Вероятностные
Детерминированные
Устойчивые
Неустойчивые
1 уровень
2 уровень
3 уровень
Слайд 21По определенности функций
Полностью определенный автомат имеет для каждого состояния входа
определенное внутреннее состояние
Слайд 22По однозначности функции перехода
В детерминированных автоматах под воздействием произвольного входного
сигнала автомат может перейти в одно и только одно состояние.
В неустойчивых автоматах переход возможен в несколько состояний при изменении состояния входа.
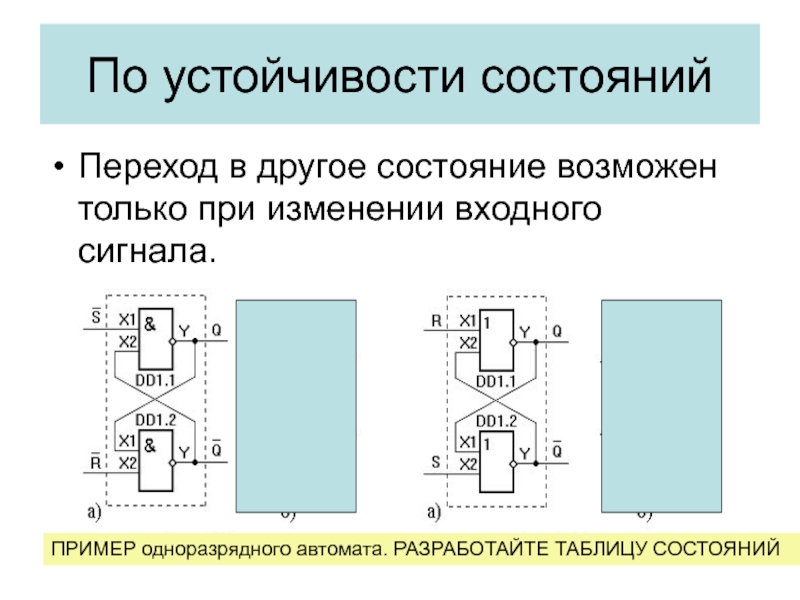
Слайд 23По устойчивости состояний
Переход в другое состояние возможен только при изменении
входного сигнала.
ПРИМЕР одноразрядного автомата. РАЗРАБОТАЙТЕ ТАБЛИЦУ СОСТОЯНИЙ
Слайд 24Понятие цифрового автомата терминология
Цифровой автомат – цифровое устройство для обработки
информации.
В цифровых автоматах принят алфавитный способ задания информации. Алфавит состоит
из букв.Конечные последовательности букв алфавита называются словами.
Число букв в слове называются длиной слова.
В алфавите из m букв можно получить
слов
Слайд 25Любой цифровой преобразователь информации можно представить в виде устройства, на
вход которого поступают слова входного алфавита, а на выходе образуются
слова выходного алфавита.Процесс преобразования информации в таком устройстве сводится к установлению соответствия входного и выходного алфавита.
Эти соответствия называют алгоритмами.
Понятие цифрового автомата терминология
Слайд 26Особенности цифрового автомата
Автомат имеет конечное множество внутренних состояний.
Переход автомата из
одного состояния в другое происходит скачкообразно или мгновенно. Но для
учета задержек в системе вводится понятие интервала дискретности, через который происходит изменение состояния.Это позволяет рассматривать работу автомата в так называемом дискретном времени, принимающем целые значения.
Слайд 27Задание алгоритма работы автомата
Множество букв входного алфавита автомата U, множество
букв выходного алфавита V, множество букв алфавита его внутренних состояний
W.На заданных множествах необходимо задать функцию переходов и
функцию выходов, тогда мы зададим алгоритм работы автомата.
Слайд 28Задание алгоритма работы автомата через функцию перехода
Функция переходов определяет состояние
автомата w(t+1) в интервале дискретности (t+1) в зависимости от его
состояния в w(t) и входного сигнала u(t).Функция переходов
Слайд 29Задание алгоритма работы автомата через функцию выхода
Функция выходов определяет выходной
сигнал v(t). Она может быть задана двумя способами.
Если выходной сигнал
в момент времени t определяется только состоянием автомата во время t, то такой автомат называется автоматом Мура.
Слайд 30Автомат Мили
Если выходной сигнал зависит не только от состояния автомата,
но и от входного сигнала, то такой автомат называют автоматом
Мили.В теории цифровых автоматов доказано что для каждого автомата
Мили существует эквивалентный ему автомат Мура. Это обстоятельство
позволяет рассматривать только автоматы Мура, как более простые.
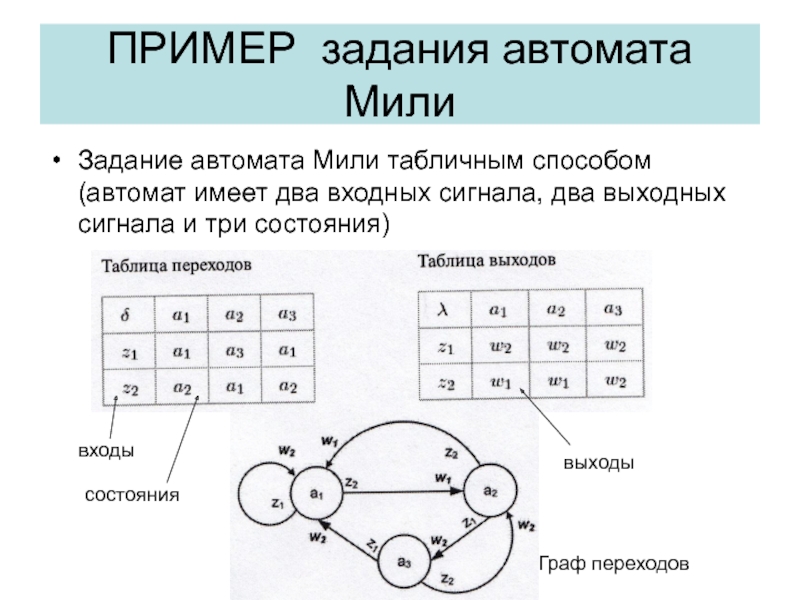
Слайд 32ПРИМЕР задания автомата Мили
Задание автомата Мили табличным способом (автомат имеет
два входных сигнала, два выходных сигнала и три состояния)
входы
состояния
выходы
Граф
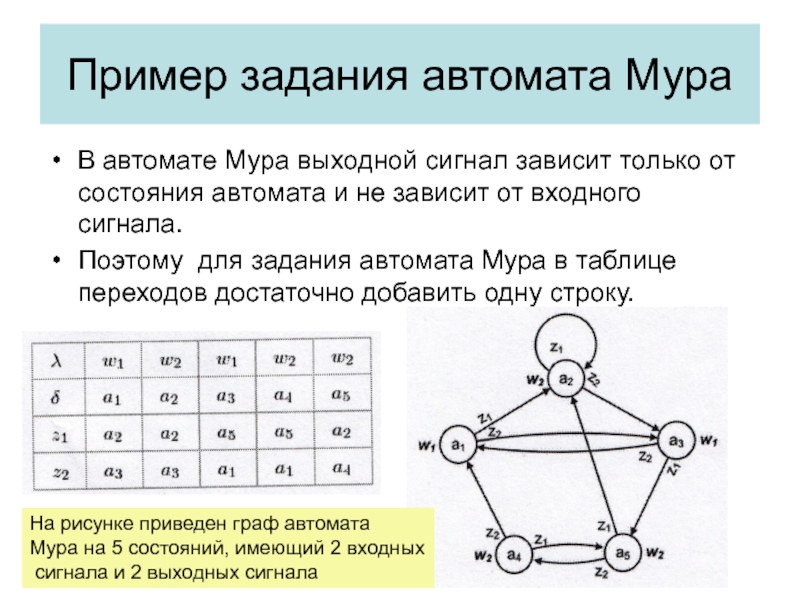
переходов
Слайд 33Пример задания автомата Мура
В автомате Мура выходной сигнал зависит только
от состояния автомата и не зависит от входного сигнала.
Поэтому для
задания автомата Мура в таблице переходов достаточно добавить одну строку.На рисунке приведен граф автомата
Мура на 5 состояний, имеющий 2 входных
сигнала и 2 выходных сигнала
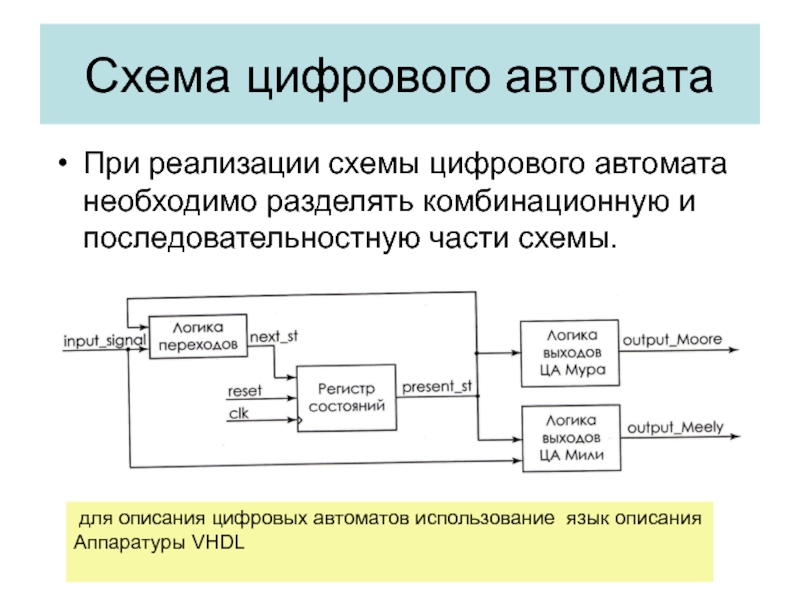
Слайд 35Схема цифрового автомата
При реализации схемы цифрового автомата необходимо разделять комбинационную
и последовательностную части схемы.
для описания цифровых автоматов использование язык
описанияАппаратуры VHDL
Слайд 36Задана таблица переходов автомата Мура. ЗАДАЧА ПОСТРОЙТЕ ГРАФ ФУНКЦИОНИРОВАНИЯ АВТОМАТА
Значение
выхода
Значение
внутреннего
состояния
автомата
в интервалы
дискретности
Интервалы дискретности
Слайд 37Граф функционирования автомата Мура
Зная таблицу переходов можно построить граф функционирования
цифрового автомата.
Вершины – это состояния выхода, а стрелки направления перехода.
Слайд 38Применение понятия цифрового автомата
Пример кодирования в двоичном алфавите десятичной системы
счисления
Слайд 39Синхронные и асинхронные автоматы
Автомат называется асинхронным, если его состояние меняется
только при изменении состояния входов.
Если вышеуказанное условие не выполняется, то
он называется синхронным.
