Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ТЕМА ЛЕКЦИИ: ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ 1.Непределенный интеграл 2. Определенный
Содержание
- 1. ТЕМА ЛЕКЦИИ: ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ 1.Непределенный интеграл 2. Определенный
- 2. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛгде f(x) – подинтегральная функция,f(x)dx – подинтегральное выражение (дифференциал),с – постоянная интегрирования.Обозначение неопределённого интеграла
- 3. Неопределенный интеграл
- 4. Таблица неопределенных интегралов
- 5. Определенный интеграл
- 6. Определенный интеграл
- 7. Определенный интеграл.
- 8. Обозначение определённого интегралагде а, в – пределы интегрирования
- 9. Криволинейная трапецияОтрезок [a;b] называют основанием этой криволинейной
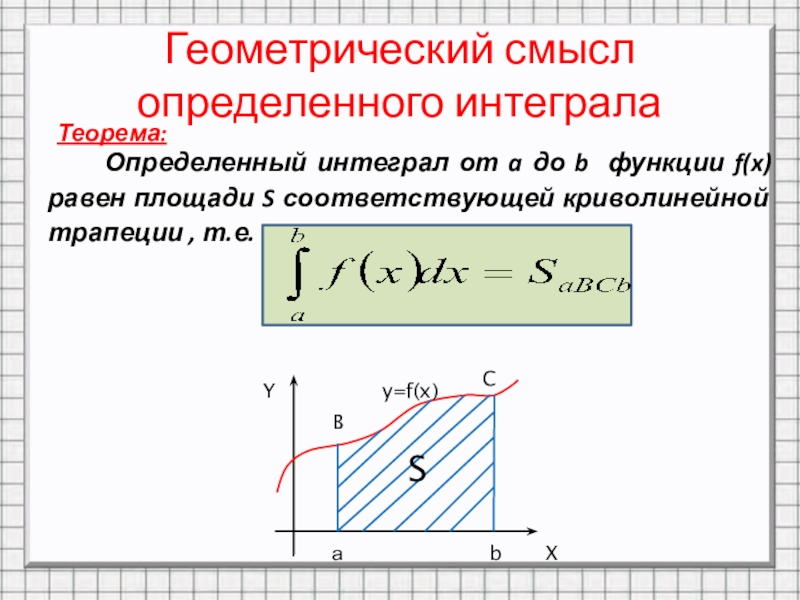
- 10. Геометрический смысл определенного интегралаТеорема: Определенный интеграл от
- 11. Свойства определенного интеграла
- 12. Свойства определенного интеграла
- 13. Формула вычисления площади с помощью интеграла
- 14. ПРАКТИКА:«ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ»
- 15. Пример
- 16. Пример
- 17. Пример
- 18. Задание 1:Вычислить интеграл
- 19. Задание 1: Вычислить интеграл
- 20. Скачать презентанцию
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛгде f(x) – подинтегральная функция,f(x)dx – подинтегральное выражение (дифференциал),с – постоянная интегрирования.Обозначение неопределённого интеграла
Слайды и текст этой презентации
Слайд 2НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
где f(x) – подинтегральная функция,
f(x)dx – подинтегральное выражение (дифференциал),
с
– постоянная интегрирования.
Слайд 9Криволинейная трапеция
Отрезок [a;b] называют основанием
этой криволинейной трапеции
Криволинейной трапецией
называется фигура,
ограниченная графиком непрерывной и не меняющей
на отрезке [а;b]
знака функции f(х), прямымих=а, x=b и отрезком [а;b].
![Криволинейная трапецияОтрезок [a;b] называют основанием этой криволинейной трапецииКриволинейной трапецией называется фигура, ограниченная графиком непрерывной и не меняющейна](/img/tmb/7/624727/979b7cf4187c29ddf5323b765326d11b-800x.jpg "ТЕМА ЛЕКЦИИ:
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
1.Непределенный интеграл
2. Определенный Криволинейная трапецияОтрезок [a;b] называют основанием этой криволинейной трапецииКриволинейной трапецией называется фигура,")
Слайд 10Геометрический смысл определенного интеграла
Теорема:
Определенный интеграл от a до b
функции f(x) равен площади S соответствующей криволинейной трапеции , т.е.
Y
X
а
b
y=f(x)
B
C
S
Слайд 13Формула вычисления площади с помощью интеграла
Пусть функция
f(x) непрерывна на отрезке [а;b] и пусть F(х) есть какая
– либо её первообразная. Тогда справедливо равенство формула Ньютона-Лейбница
![Формула вычисления площади с помощью интеграла Пусть функция f(x) непрерывна на отрезке [а;b] и пусть](/img/tmb/7/624727/d769c735ae1ab607260bb3075a969a72-800x.jpg "ТЕМА ЛЕКЦИИ:
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
1.Непределенный интеграл
2. Определенный Формула вычисления площади с помощью интеграла Пусть функция f(x) непрерывна")
