Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема: Понятия
Содержание
- 1. Тема: Понятия
- 2. Цель: математически грамотное определение понятий.Знать: определения следующих
- 3. Понятие о понятии1
- 4. «Однажды Элфи пришла домой и говорит своей
- 5. Свойство, которым обладает предмет или которое можно
- 6. Признаки, которые присущи объекту; без них он
- 7. Понятие – это мысль о предмете, выделяющая
- 8. Слово является носителем понятия.Понятие и слово не
- 9. !Составить понятие об объекте – значит уметь
- 10. Понятия, связанные с числами и операциями
- 11. «любовь»«влюбленный юноша»«влюбленная девушка»«прилежание»«прилежный ученик»«доброта»«добрый мальчик»Классифицируйте следующие понятия:
- 12. Объем и содержание понятия2
- 13. Объем и содержание понятия
- 14. «Треугольник»«Прямоугольный треугольник»S={три стороны, три угла, три вершины,…,
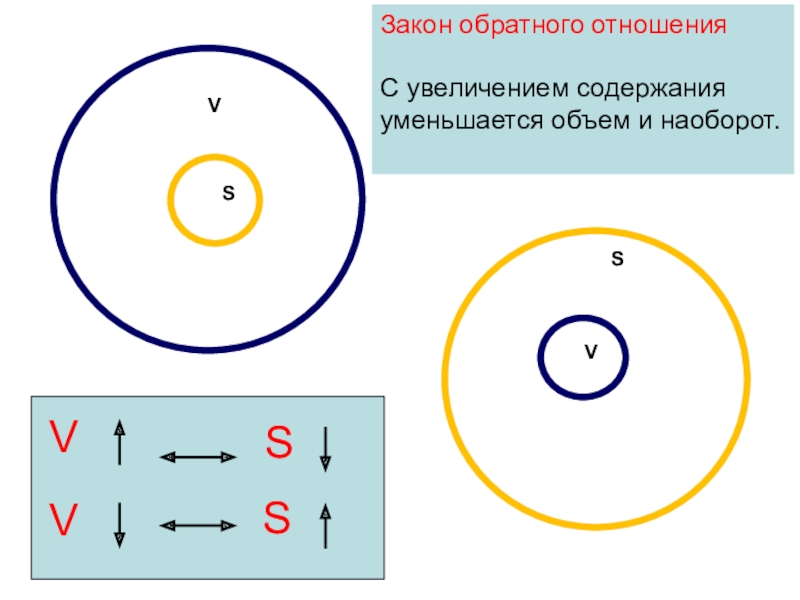
- 15. Закон обратного отношенияС увеличением содержания уменьшается объем и наоборот.
- 16. объем понятия – пустое множествов объем понятия
- 17. Слайд 17
- 18. Отношения между понятиями3
- 19. Отношения между понятиямив содержании имеются общие признакиНапример:
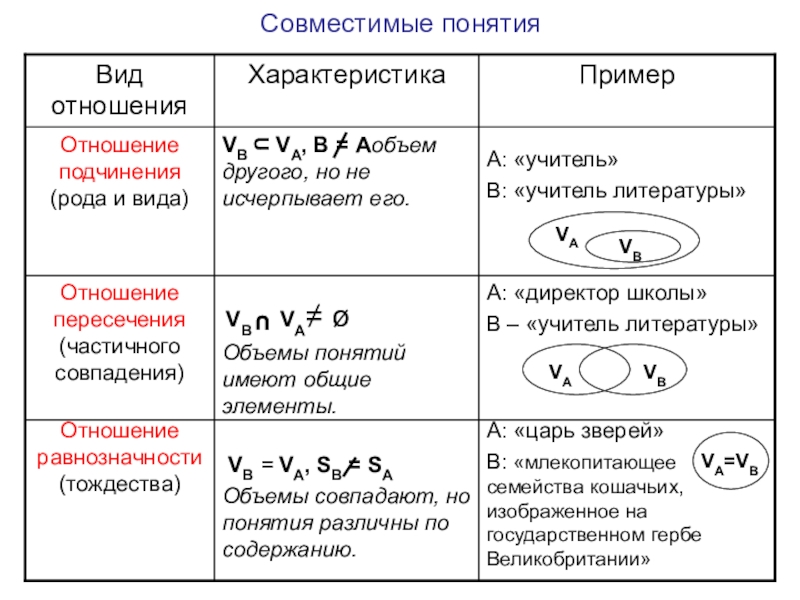
- 20. Совместимые понятия VB = VA, SВ = SАОбъемы совпадают, но понятия различны по содержанию.
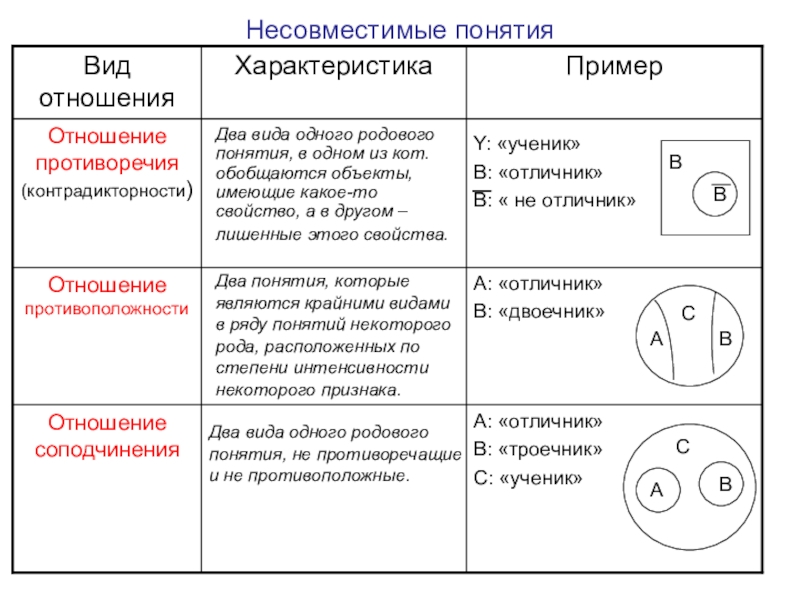
- 21. Несовместимые понятия
- 22. Проверь себя! Определите вид отношений между понятиями«палец»
- 23. Ответы«палец» - «перст»«инструмент»- «линейка»- «циркуль»«четырехугольник»- «прямоугольник»- «ромб»«одежда»-
- 24. Определите вид отношения, начертите диаграмму Эйлера-Венна для
- 25. Ограничение и обобщение понятий Ограничение – логическая
- 26. Определение понятия4
- 27. « В споре рождается истина»… СократСократ родился
- 28. Определение понятия – это логическая операция, которая
- 29. Определения понятийЯвныеНеявныеконтекстуальноеостенсивноеатрибутивноегенетическоеоперационноеаксиоматическоеиндуктивное
- 30. Неявные определенияСодержание определяемого понятия раскрывается опосредованно (косвенно).контекстуальноеостенсивноеСодержание
- 31. «Ломаная линия не похожа на прямую линию,
- 32. Явные определенияИмеют форму равенства: определяемое понятие равно
- 33. Для определения всегда берётся ближайший род и
- 34. Акваланг – это устройство для дыхания человека
- 35. «Человек – это животное без перьев» (Сократ)Требования
- 36. 1. «Человек – это млекопитающее, умеющее решать
- 37. 2. Отсутствие порочного круга (тавтологии) в тексте
- 38. 3. Определение должно быть ясным (доступным пониманию)Без
- 39. 4. Определение должно содержать ближайший род«Квадрат –
- 40. 6. По возможности, не должно быть отрицания.НО!
- 41. Фанфаронство – поведение фанфарона.Число b называется делителем
- 42. Как дать определение понятиюНазвать определяемое понятие (подобрать
- 43. Насекомые – маленькие членистоногие беспозвоночные животные. Посуда
- 44. Какие задачи стоят перед определением?В чем сходны
- 45. Задачи определения.Явные определения и требования к ним.Неявные
- 46. Горский Д.П. Определение. — М.,1985.Горский Д.П., Ивин
- 47. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Тема: «Понятия»
«Понятие - это то, что раскрывает, что есть,
или чем бывает тот или иной предмет».
Слайд 2Цель: математически грамотное определение понятий.
Знать: определения следующих понятий: «понятие», «термин»,
«содержание понятия», «объем понятия»; виды отношений между понятиями; виды определений;
требования к определениям понятий.Понимать закон обратного отношения между объемом и содержанием понятия; что понятия могут находиться в разных отношениях; структуру формально-логического определения.
Применять: определять вид отношений между понятиями, определять понятия, опираясь на требования к определениям.
Анализировать: грамотность составленного определения (работа в парах).
Синтезировать: составлять пары понятий заданного вида, составлять определения изучаемых понятий.
Оценивать: математическую грамотность предъявленных определений, опираясь на заданные критерии.
Слайд 4«Однажды Элфи пришла домой и говорит своей старшей сестре: –
Кати, у нас будет соревнование, кто умеет лучше различать. Ты
знаешь, что-нибудь о различиях?.. – Я знаю историю, – говорит она. – Может быть, это о различиях. – Расскажи мне ее, – попросила Элфи. – Пожалуйста. – Хорошо. Жили-были два близнеца, понятно? Их звали Твидлдум и Твидлдам. Они выглядели совершенно одинаковыми. – О, я знаю! – закричала Элфи. – Проблема в том, как их различить. А ответ: по именам! – Помолчи, Элфи! Дай мне закончить историю, – перебила Кати. – На их день рождения родители подарили Твидлдуму большого красного пони, а Твидлдаму маленького зеленого утенка. Но близнецы не могли различить животных. Поэтому они повязали голубую ленточку вокруг шеи пони и зеленую ленточку вокруг шеи утенка. После этого они смогли их прекрасно отличать. – Кати! – закричала Элфи. – Какая глупая история! Как она сможет научить меня уметь хорошо различать? – Может быть, она научит тебя, что значит не уметь различать? Элфи покачала головой: – Кати, если завязать голубую ленточку Твидлдаму, а зеленую – Твидлдуму? – то это было бы хорошим способом различать их. Не так ли? Но почему же это не годится для различения пони и уточки?..»Слайд 5
Свойство, которым обладает предмет или которое можно приписать предмету, называется
признаком.
Например:
«… «пироги» (довольно часто) обладают признаком «подгорелые», а «мальчики»,(в исключительных
случаях) - признаком «милые»». Л.Кэрролл
Слайд 6Признаки, которые присущи объекту; без них он не может существовать.
Признаки,
отсутствие которых не влияет на существование объекта.
Цвет, размер, положение в
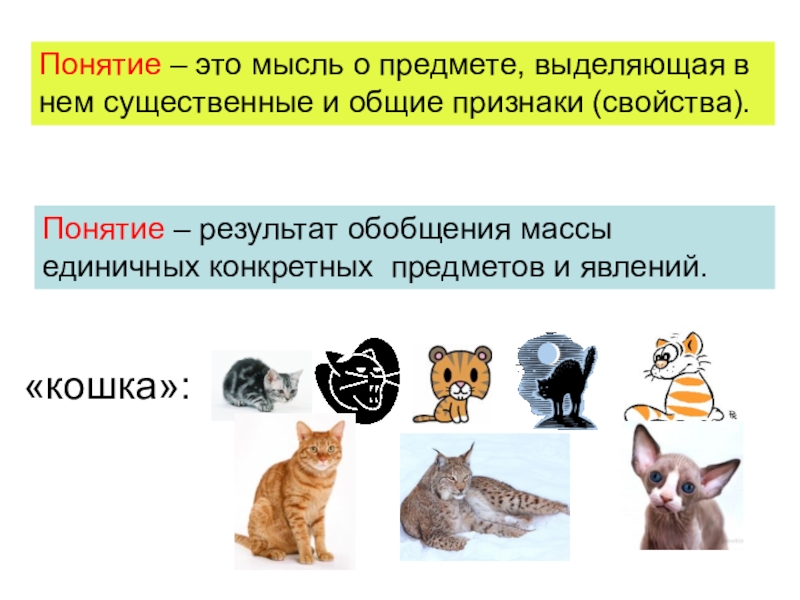
пространстве,…Слайд 7Понятие – это мысль о предмете, выделяющая в нем существенные
и общие признаки (свойства).
Понятие – результат обобщения массы единичных конкретных
предметов и явлений.«кошка»:
Слайд 8Слово является носителем понятия.
Понятие и слово не тождественны.
Слово, обозначающее строго
определенное понятие какой-либо области науки, техники, называется термином.
В математике схожесть
в зависимости от ситуации обозначается разными терминами: подобие
равенство
тождество
конгруэнтность*
равномощность
эквивалентность и др.
Слайд 9!
Составить понятие об объекте – значит уметь отличать его от
других, сходных
с ним предметов.
Особенности математических объектов:
Математический объект реально не
существует.Это идеальные объекты, созданные умом человека.
2) При использовании термина имеется в виду вся совокупность объектов.
Слайд 10Понятия, связанные с числами и операциями над ними: «число», «сложение»,
«слагаемые»,
«больше» и подобные этим.
Понятия алгебраические: «выражение», «равенство», «неравенство», «уравнение»
и т. д.Геометрические понятия: «точка», «прямая», «отрезок», « треугольник» и т.д.
Понятия, связанные с величинами и их измерениями: «длина», «сантиметр», «гектар», «килограмм» и т.д.
Математические понятия в начальной школе
х + 23 = 78
Слайд 11«любовь»
«влюбленный юноша»
«влюбленная девушка»
«прилежание»
«прилежный ученик»
«доброта»
«добрый мальчик»
Классифицируйте следующие понятия:
Слайд 14«Треугольник»
«Прямоугольный
треугольник»
S={три стороны, три угла, три вершины,…, сумма внутренних углов
1800,…}
S={три стороны, три угла, три вершины,…, сумма внутренних углов
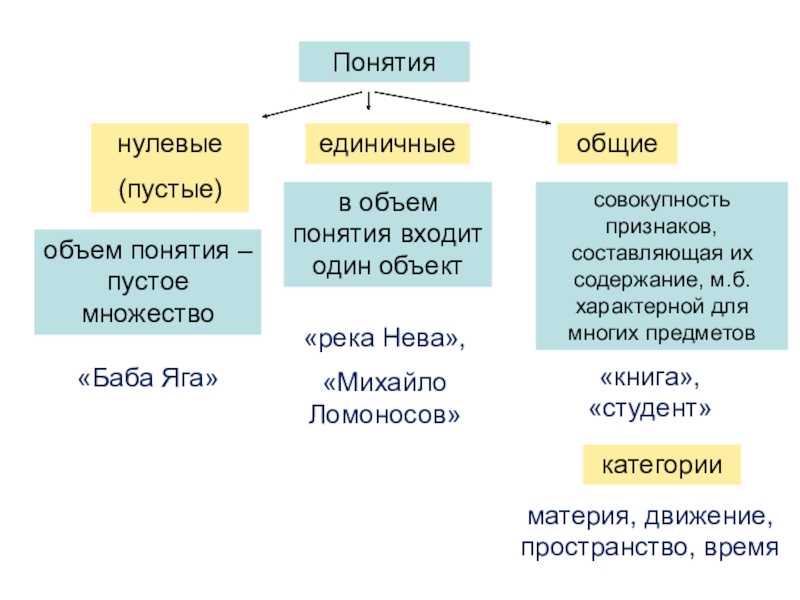
1800,…,один угол 900, катет, гипотенуза, квадрат гипотенузы равен сумме квадратов катетов,… } Слайд 16объем понятия – пустое множество
в объем понятия входит один объект
совокупность
признаков, составляющая их содержание, м.б. характерной для многих предметов
категории
материя, движение,
пространство, время«река Нева»,
«Михайло Ломоносов»
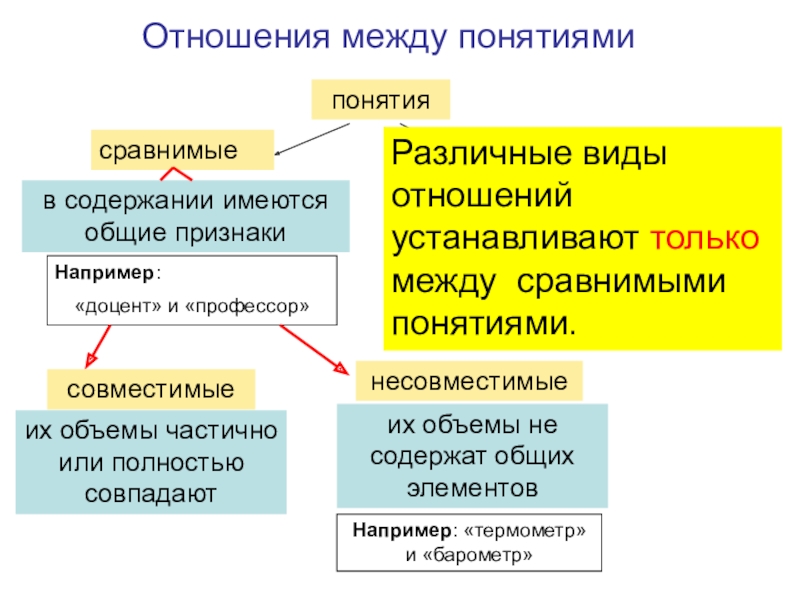
Слайд 19Отношения между понятиями
в содержании имеются общие признаки
Например:
«доцент» и «профессор»
их
объемы частично или полностью совпадают
содержание не имеет общих признаков
Например:
«океан» и «5»их объемы не содержат общих элементов
Например: «термометр» и «барометр»
Различные виды отношений устанавливают только между сравнимыми понятиями.
Слайд 22Проверь себя!
Определите вид отношений между понятиями
«палец» - «перст»
«инструмент»- «линейка»- «циркуль»
«четырехугольник»-
«прямоугольник»- «ромб»
«одежда»- «халат»
«полночь» - «полдень»
«глаз»- «око»
«карандаш»- «ручка»
«учитель»- «женщина»
«русский»- «нерусский»
«русак»- «млекопитающее»-
«заяц»Слайд 23Ответы
«палец» - «перст»
«инструмент»- «линейка»- «циркуль»
«четырехугольник»- «прямоугольник»- «ромб»
«одежда»- «халат»
«полночь» - «полдень»
«глаз»-
«око»
«карандаш»- «ручка»
«учитель»- «женщина»
«русский»- «нерусский»
«русак»- «млекопитающее»- «заяц»
равнозначности
соподчинения
пересечения
подчинения
противоположности
равнозначности
соподчинения
пересечения
противоречия
подчинения
Каждый правильный ответ –
0,5 баллаСлайд 24Определите вид отношения, начертите диаграмму Эйлера-Венна для понятий:
а) «далекий»,
«недалекий»;
б) «далекий, близкий»;
в) «равносторонний треугольник», «Равноугольный треугольник»;
г)
«СМИ», «ТВ», «радио»; д)«человек», «врач», «больной»;
е) «число», «целое число», «дробное число».
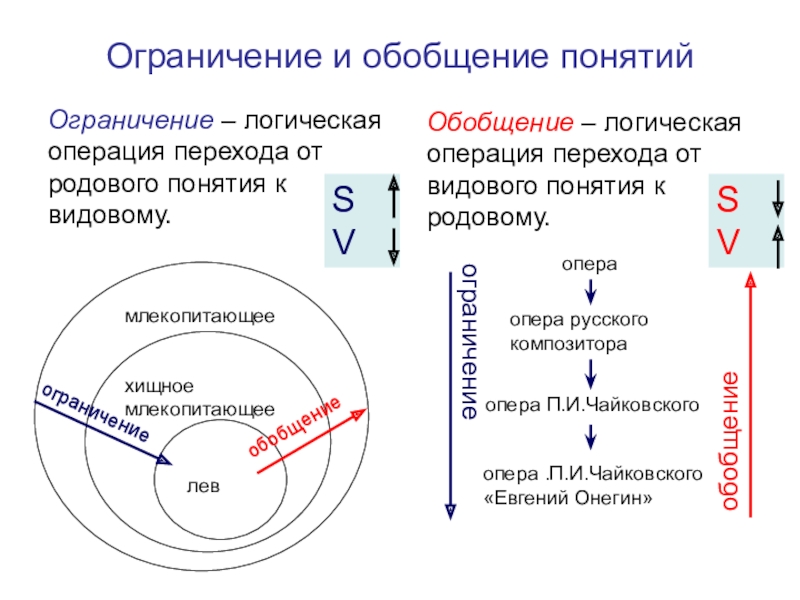
Слайд 25Ограничение и обобщение понятий
Ограничение – логическая операция перехода от
родового понятия к видовому.
Обобщение – логическая операция перехода от видового
понятия к родовому.лев
хищное млекопитающее
млекопитающее
опера .П.И.Чайковского «Евгений Онегин»
опера П.И.Чайковского
опера русского композитора
опера
S V
S V
Слайд 27« В споре рождается истина»…
Сократ
Сократ родился в Афинах в 470
г. до н.э.
Его отец, Софроникс, был каменотесом, а мать
— повитухой.Сократ любил говорить, что унаследовал от матери ее искусство, сравнивая его с философским методом – майевтикой: “Теперь мое повивальное искусство во всем похоже на акушерское, отличаясь от него лишь тем, что я принимаю роды у мужей, а не у жен, роды души, а не тела”.
Слайд 28Определение понятия – это логическая операция, которая раскрывает содержание понятия
либо устанавливает значение термина.
Определить понятие — значит указать, что оно
означает, выявить признаки, входящие в его содержание..
«кисть»
Одним из самых надежных способов, предохраняющих от недоразумений в общении, исследовании, споре, является определение, или дефиниция.
Цель определения — уточнение содержания используемых понятий.
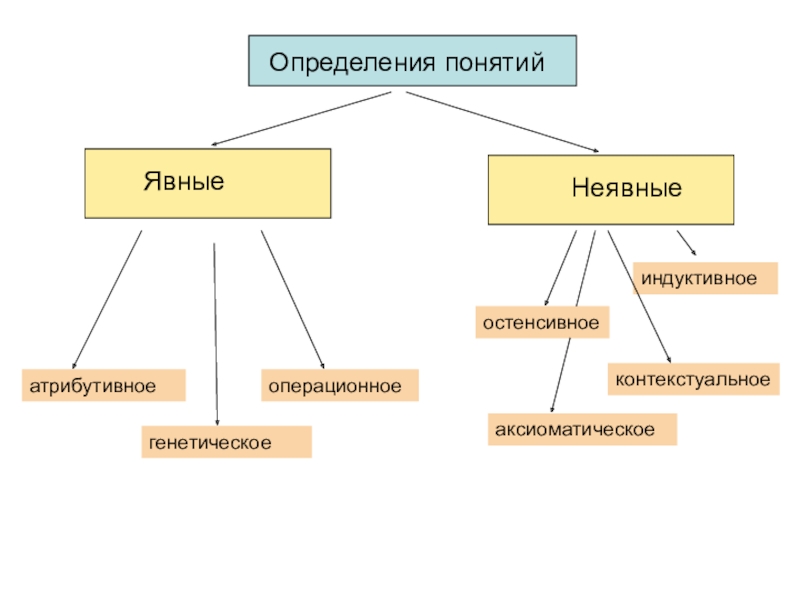
Слайд 29Определения понятий
Явные
Неявные
контекстуальное
остенсивное
атрибутивное
генетическое
операционное
аксиоматическое
индуктивное
Слайд 30Неявные определения
Содержание определяемого понятия раскрывается опосредованно (косвенно).
контекстуальное
остенсивное
Содержание понятия раскрывается через
отрывок текста, контекст (общий смысл), анализ приведенной ситуации.
Определение объекта через
показ, демонстрацию.Суть: показать и назвать.
«Мы из всех заданий выбрали текстовые задачи, а из них выбрали задачи, которые решаются одним арифметическим действием. Это и есть простые задачи».
Это - слон
Самые распространённые
Слайд 31«Ломаная линия не похожа на прямую линию, но её тоже
чертят по линейке. Узнаем почему.
Ломаные линии составлены из отрезков.
Эти отрезки – звенья ломаной. У ломаной линии конец одного отрезка – начало другого, кроме концов ломаной. Никакие два соседние звена не лежат на одной прямой. Концы каждого звена – вершины ломаной. …»Ломаные на рисунке 1 называются незамкнутыми, а на рисунке 2 – замкнутыми.
Тема «Ломаная линия», учебник 1 класса, часть 1, авторы Моро М.И., Волкова С.И., Степанова С.В.
?
?
Слайд 32Явные определения
Имеют форму равенства: определяемое понятие равно определяющему понятию.
«А
есть В» или «А = В»
Самые распространённые
Через род и видовое
отличиеКвадратом называется прямоугольник с равными сторонами.
определяемое
понятие
определяющее понятие
род
видовое отличие
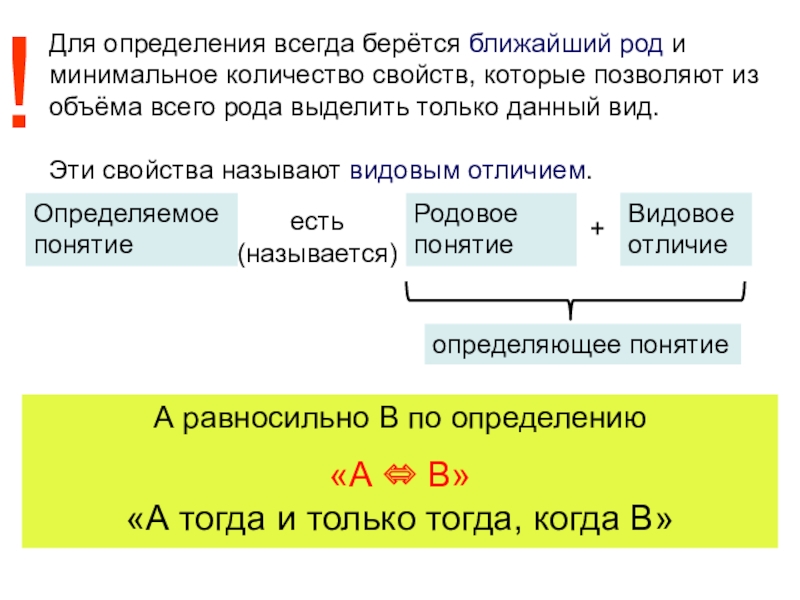
Слайд 33Для определения всегда берётся ближайший род и минимальное количество свойств,
которые позволяют из объёма всего рода выделить только данный вид.
Эти свойства называют видовым отличием.
А равносильно В по определению
«А В»
«А тогда и только тогда, когда В»
!
Слайд 34Акваланг – это устройство для дыхания человека под водой.
Кинотеатр –
это помещение, в котором демонстрируются кинофильмы.
Молекула есть мельчайшая частица вещества,
сохраняющая все химические свойства этого вещества.Логика – это наука о законах и формах мышления.
Многоугольник – простая замкнутая ломаная линия.
Четырёхугольник – многоугольник с четырьмя углами.
Числа, получаемые при счёте, называются натуральными.
Лицевая сторона монеты или медали – аверс.
Гросс – счётная единица в двенадцатеричной системе счисления, двенадцать дюжин.
?
Слайд 35«Человек – это животное без перьев» (Сократ)
Требования к определениям
1. Соразмерность
(объемы
определяемого и определяющего понятий должны совпадать).
«А В»
Проверка соразмерности:
А
В: Каждый человек – животное без перьев (истинно).
В А: Каждое животное без перьев – человек (ложно). Определение несоразмерно, так как не всякое животное без перьев можно назвать человеком.
Слайд 361. «Человек – это млекопитающее, умеющее решать квадратные уравнения»
Определение
несоразмерное, так как некоторых школьников поневоле пришлось бы не считать
за людей.2. «Лимонад – это прохладительный газированный напиток с соком лимона или других фруктов и ягод»
Определение соразмерное.
?
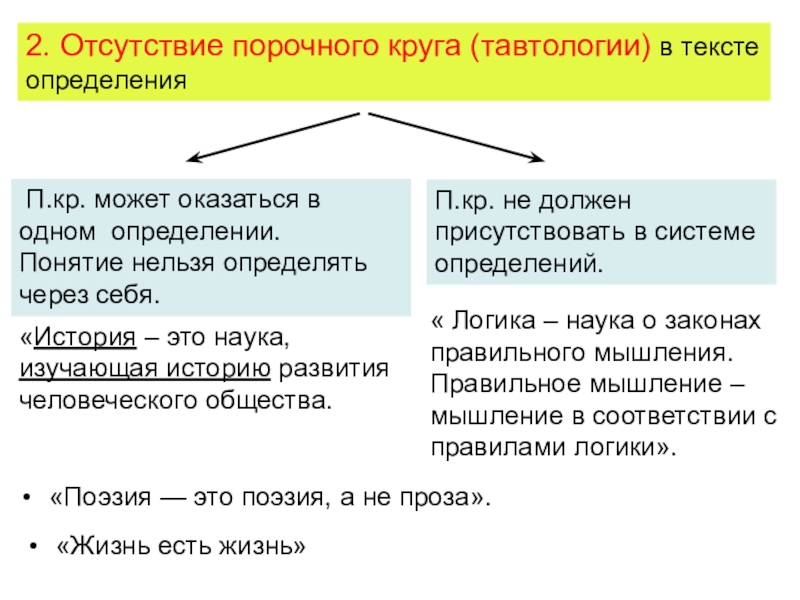
Слайд 372. Отсутствие порочного круга (тавтологии) в тексте определения
«История – это
наука, изучающая историю развития человеческого общества.
« Логика – наука о
законах правильного мышления. Правильное мышление – мышление в соответствии с правилами логики».
«Жизнь есть жизнь»
«Поэзия — это поэзия, а не проза».
П.кр. может оказаться в одном определении.
Понятие нельзя определять через себя.
П.кр. не должен присутствовать в системе определений.
Слайд 383. Определение должно быть ясным (доступным пониманию)
Без двусмысленностей.
«Дети
– цветы жизни».
Термины, употребляемые в определении должны быть известны.
«Анахромат
– объектив, в котором не устранены хроматические аберрации». Определение должно содержать достаточное количество свойств, чтобы выделить нужные объекты, но без избыточных свойств, т. е. тех свойств, которые можно вывести из других указанных свойств.
«Квадрат – ромб с прямым углом и равными диагоналями».
Слайд 394. Определение должно содержать ближайший род
«Квадрат – это четырехугольник, у
которого все стороны равны и все углы прямые»
( верный
выбор: «квадрат – это ромб с прямым углом» или «квадрат – это прямоугольник с равными смежными сторонами»).5. Определяемое и определяющее понятия должны принадлежать к одной семантической категории
«Отличник – это получать одни пятерки».
Слайд 406. По возможности, не должно быть отрицания.
НО! «Параллельными называют прямые,
лежащие в одной плоскости и НЕ имеющие общих точек».
Слайд 41Фанфаронство – поведение фанфарона.
Число b называется делителем числа а, если
остаток от деления а на b равен 0.
Факультатив – факультативный
предмет, курс в учебном заведении.Параллелограммом называется четырёхугольник, противоположные стороны которого равны и параллельны (Из учебника «Математика» Дадаяна А.А.)
Високосным называют год, содержащий 366 дней и в феврале которого 29 дней.
Школьник – ребёнок в возрасте от 6 до 17 лет.
Число, которое не делится на 2, называется нечётным.
Отличник – учащийся, который среди итоговых отметок не имеет ни «2», ни «3», ни «4».
Эквиваленцией высказываний называют конъюнкцию двух взаимно обратных импликаций.
Кубом называют многогранник.
?
Слайд 42Как дать определение понятию
Назвать определяемое понятие (подобрать слово, термин).
Указать для
определяемого понятия ближайшее родовое понятие.
Перечислить свойства, которые выделяют определяемое
понятие из объектов его рода, т.е. сформулировать видовое отличие.Проверить, выполнены ли требования к определению понятий.
Слайд 43Насекомые –
маленькие членистоногие беспозвоночные животные.
Посуда –
хозяйственная утварь
для еды, питья, хранения припасов.
Фрукт –
сочный съедобный плод какого-то
дерева. Деревья –
многолетние растения с твердым стволом и отходящими от него ветвями, образующими крону.
Оружие –
средство или приспособление, технически пригодное для нападения или защиты.
Млекопитающие –
позвоночные животные, вскармливающие своих детенышей молоком.
Инструмент –
ручное орудие для производства каких-либо работ.
Обувь –
изделие из кожи или других материалов, обычно с твердой подошвой, носимое на ногах.
?
Слайд 44Какие задачи стоят перед определением?
В чем сходны контекстуальные и остенсивные
определения?
В каких случаях применимо аксиоматическое определение?
Каким требованиям должно удовлетворять явное
определение?В чем различие между номинальными и реальными определениями?
Чем различаются споры об определениях-описаниях и определениях-требованиях?
Какова роль определений в придании ясности системе понятий?
Контрольные вопросы
Слайд 45Задачи определения.
Явные определения и требования к ним.
Неявные определения.
Реальные и номинальные
определения.
Споры об определениях.
Границы эффективных определений.
Роль определений в науке.
Темы рефератов и
докладовНа дополнительные баллы по желанию
Слайд 46Горский Д.П. Определение. — М.,1985.
Горский Д.П., Ивин А.А., Никифоров А.Л.
Краткий словарь по логике. — М., 1991.
Ивин А. А. Искусство
правильно мыслить. — М.,1990.Ивин А.А. Практическая логика. Задачи и упражнения. — М., 1996.
Попа К. Определение. — М.,1976.
Сопер П. Л . Основы искусства речи. — М.,1995.
литература