если для любого значения x, взятого из области определения функции,
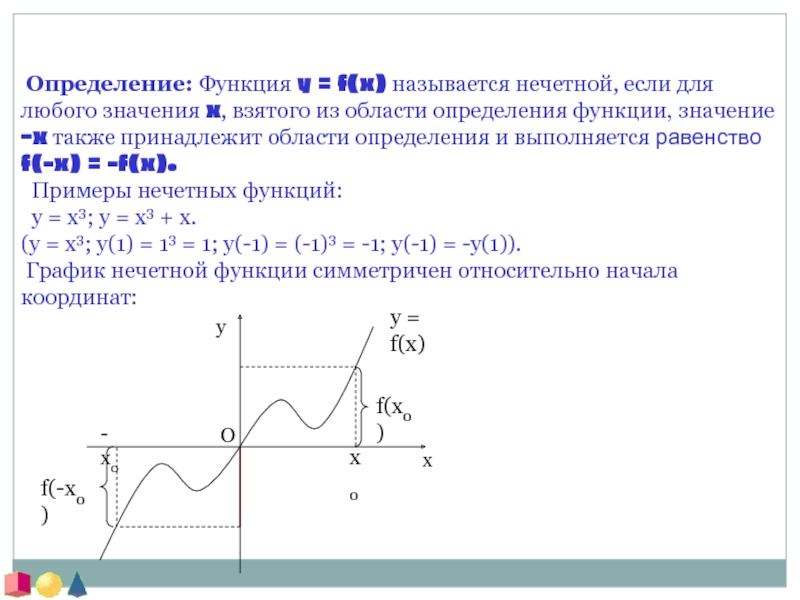
значение –x также принадлежит области определения и выполняется равенство f(-x) = f(x).Примеры четных функций:
y = x2; y = x2 + 5; y = -3x2 + 1; y = ½x½; y = 3.
(y = x2; y(1) = 12 = 1; y(-1) = (-1)2 = 1; y(1) = y(-1)).
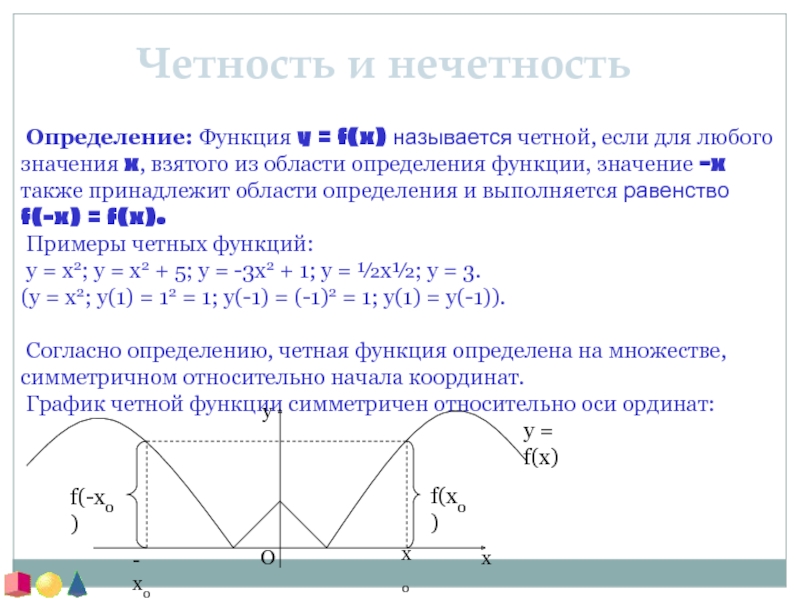
Согласно определению, четная функция определена на множестве, симметричном относительно начала координат.
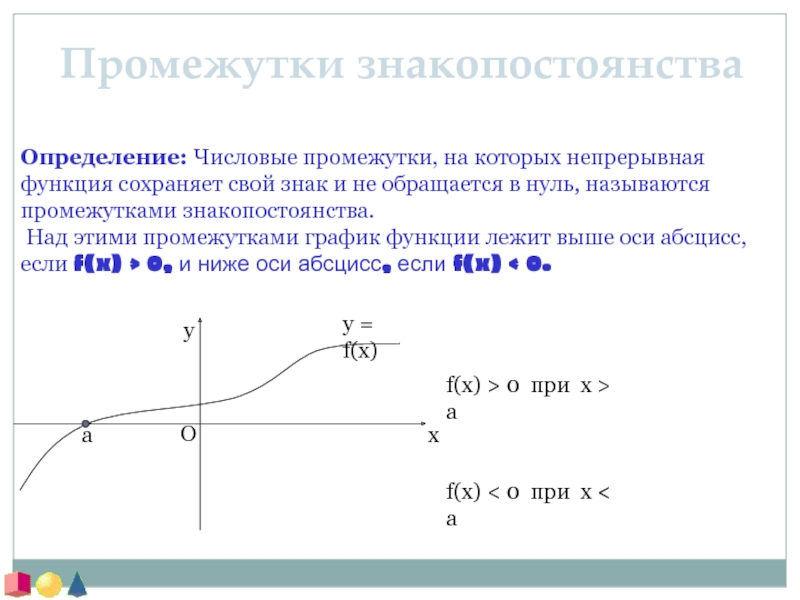
График четной функции симметричен относительно оси ординат:
y
x
O
x0
- x0