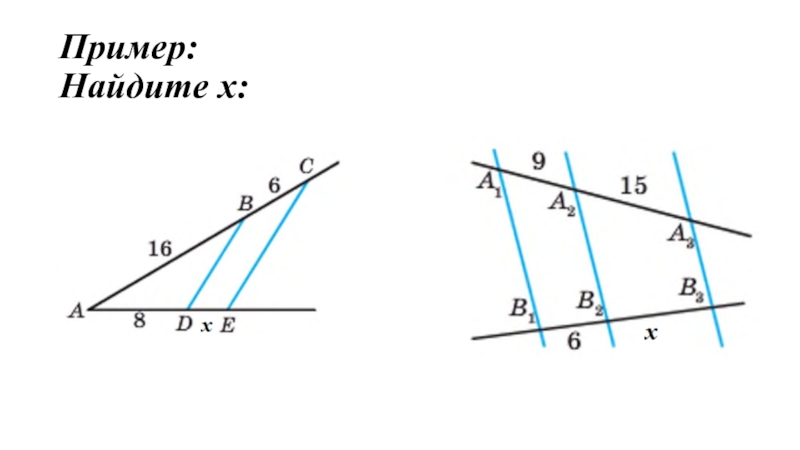Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорема Фалеса
Содержание
- 1. Теорема Фалеса
- 2. Цели обучения:8.3.1.7 знать и применять теорему Фалеса;8.3.1.8
- 3. Критерии оценивания:знает формулировку и доказательство теоремы Фалесаприменяет
- 4. Фале́с (др.-греч. Θαλῆς ὁ Μιλήσιος, 640/624 — 548/545
- 5. Теорема ФалесаА1А2А3В1В2В3ЕFЕсли параллельные прямые, пересекающие стороны угла,
- 6. АВС••••CDFED1C1E1AC1=C1D1=D1E1=E1BПусть отрезок АВ требуется разделить например на
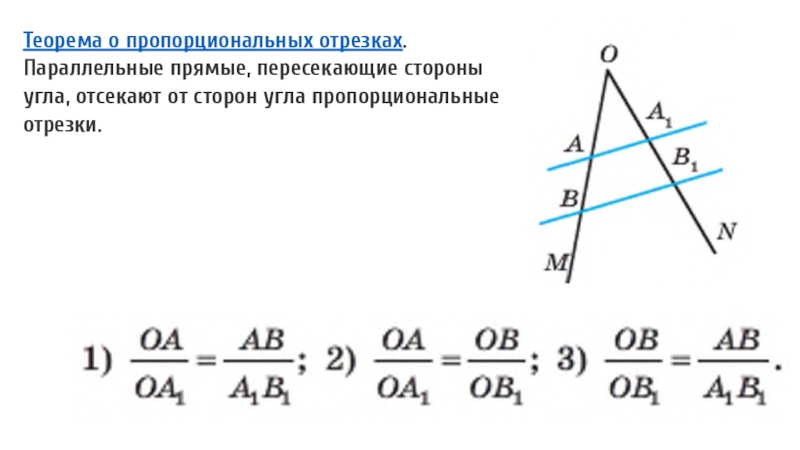
- 7. Теорема о пропорциональных отрезках. Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.
- 8. Пример: Найдите x:
- 9. 1. Параллельные прямые а и b пересекают
- 10. Слайд 10
- 11. Дано: отрезок MN. Разделите его на 5
- 12. Скачать презентанцию
Цели обучения:8.3.1.7 знать и применять теорему Фалеса;8.3.1.8 знать и применять теорему о пропорциональных отрезках;8.3.1.9 делить отрезок на n равных частей с помощью циркуля и линейки, строить пропорциональные отрезки;
Слайды и текст этой презентации
Слайд 2Цели обучения:
8.3.1.7 знать и применять теорему Фалеса;
8.3.1.8 знать и применять
теорему о пропорциональных отрезках;
с помощью циркуля и линейки, строить пропорциональные отрезки;
Слайд 3Критерии оценивания:
знает формулировку и доказательство теоремы Фалеса
применяет теорему Фалеса для
определения длин пропорциональных отрезков
применяет теорему Фалеса для доказательства подобия фигур
знает
теорему о пропорциональных отрезках;применяют теорему о пропорциональных отрезках.
знают алгоритм построения пропорциональных отрезков;
умеют строить пропорциональные отрезки.
Слайд 4Фале́с (др.-греч. Θαλῆς ὁ Μιλήσιος, 640/624 — 548/545 до н. э.) —
древнегреческий философ и математик из Милета (Малая Азия). Представитель ионической
натурфилософии и основатель милетской (ионийской) школы, с которой начинается история европейской науки. Традиционно считается основоположником греческой философии (и науки) — он неизменно открывал список «семи мудрецов», заложивших основы греческой культуры и государственностиhttps://ru.wikipedia.org/wiki/%D0%A4%D0%B0%D0%BB%D0%B5%D1%81_%D0%9C%D0%B8%D0%BB%D0%B5%D1%82%D1%81%D0%BA%D0%B8%D0%B9
Слайд 5Теорема Фалеса
А1
А2
А3
В1
В2
В3
Е
F
Если параллельные прямые, пересекающие стороны угла, отсекают на одной
его стороне равные отрезки, то они отсекают равные отрезки и
на другой его стороне.Доказательство:
1. Проведем через точку В2 прямую EF || A1A3
2. По свойству параллелограмма А1А2 = EB2,
A2A3 = FB2
4. Треугольники В2В1Е и В2В3F равны по
второму признаку:
В2F = В2Е по доказанному
Углы при вершине В2 равны как вертикальные
В1ЕВ2 = B3FB2, как внутренние накрест лежащие при параллельных прямых А1В1 и А3В3 и секущей EF
5. Из равенства треугольников следует равенство соответствующих элементов => В1В2 = В2В3 ЧТД
Дано: угол, параллельные прямые
пересекают стороны угла, А1А2 = А2А3
Доказать: В1В2 = В2В3
Слайд 6А
В
С
•
•
•
•
C
D
F
E
D1
C1
E1
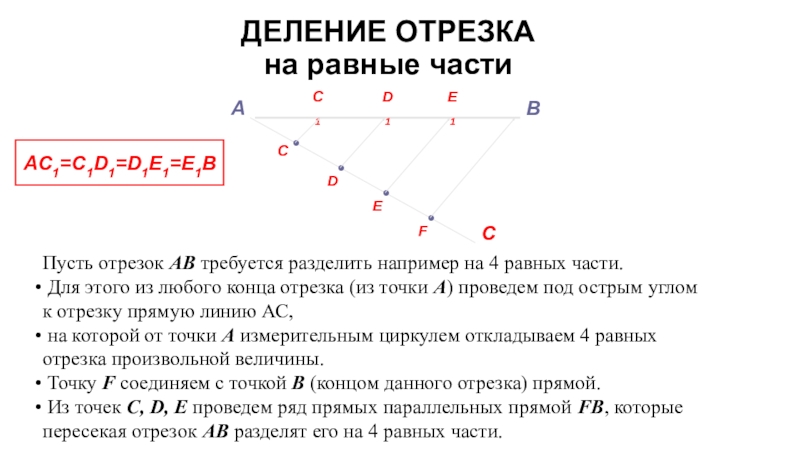
AC1=C1D1=D1E1=E1B
Пусть отрезок АВ требуется разделить например на 4 равных части.
Для этого из любого конца отрезка (из точки А) проведем
под острым углом к отрезку прямую линию АС,на которой от точки А измерительным циркулем откладываем 4 равных отрезка произвольной величины.
Точку F соединяем с точкой В (концом данного отрезка) прямой.
Из точек C, D, E проведем ряд прямых параллельных прямой FB, которые пересекая отрезок АВ разделят его на 4 равных части.
ДЕЛЕНИЕ ОТРЕЗКА
на равные части
Слайд 7Теорема о пропорциональных отрезках. Параллельные прямые, пересекающие стороны угла, отсекают
от сторон угла пропорциональные отрезки.
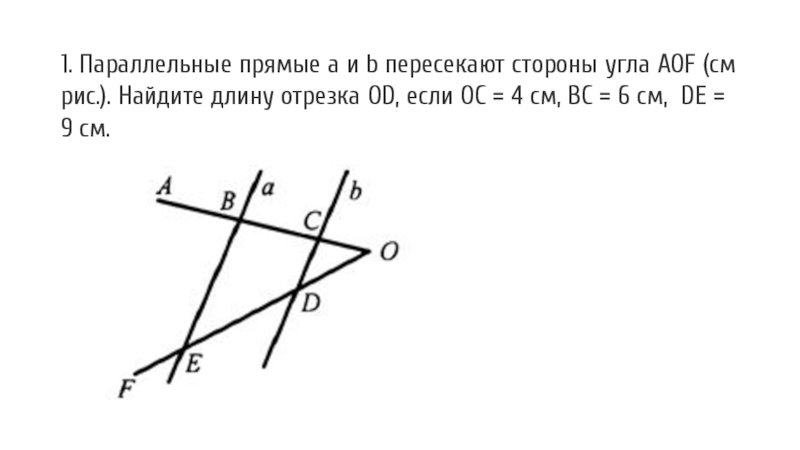
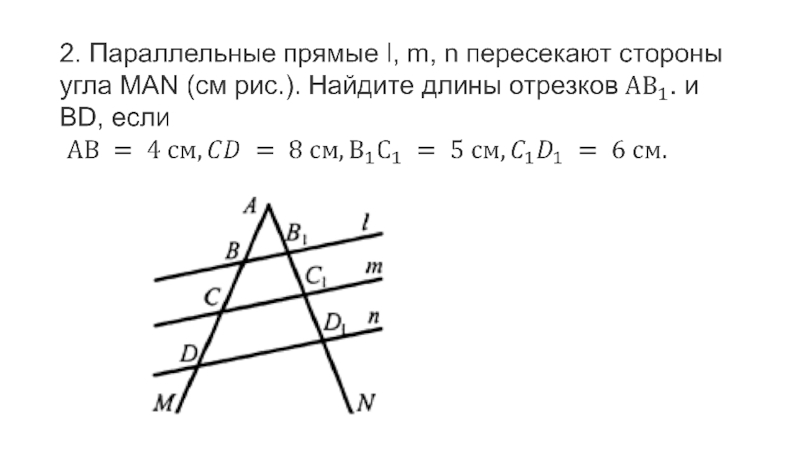
Слайд 91. Параллельные прямые а и b пересекают стороны угла АОF
(см рис.). Найдите длину отрезка OD, если ОС = 4
см, ВС = 6 см, DE = 9 см.
Слайд 11Дано: отрезок MN. Разделите его на 5 раных частей с
помощью циркуля и линейки, используя Теорему Фалеса
В треугольнике АВС сторона
АВ равна 18 см. Сторону ВС разделили на 3 равные части и из этих точек к стороне АС провели прямые параллельные к стороне АВ. Найдите длины отрезков, расположенных между сторонами треугольника.На одной стороне угла расположены отрезки, равные 3см и 4см. К второй стороне проведены параллельные прямые через крайнюю точку этих отрезков. Наибольший из двух образованных отрезков равен 6 см. Найдите длину меньшего отрезка.
Home work
