Слайд 1Теория графов: основные понятия и определения
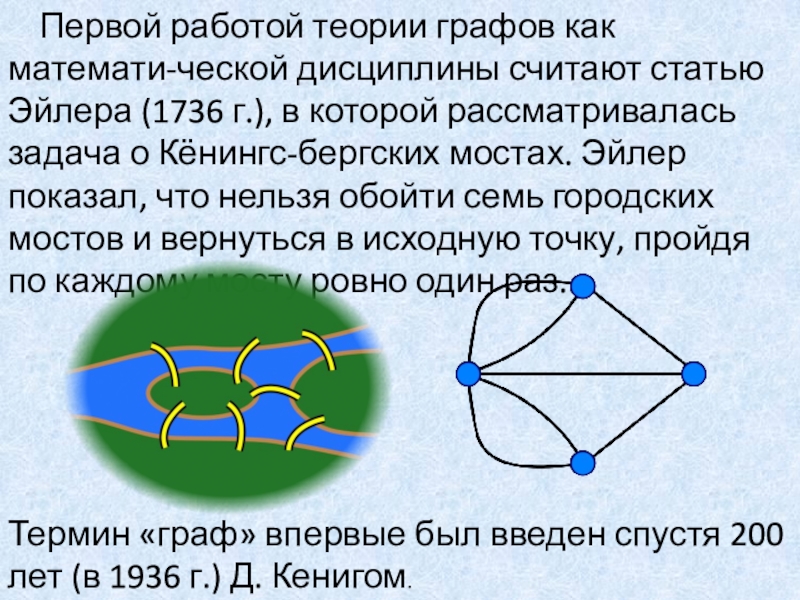
Слайд 2Первой работой теории графов как математи-ческой дисциплины считают статью Эйлера
(1736 г.), в которой рассматривалась задача о Кёнингс-бергских мостах. Эйлер
показал, что нельзя обойти семь городских мостов и вернуться в исходную точку, пройдя по каждому мосту ровно один раз.
Термин «граф» впервые был введен спустя 200 лет (в 1936 г.) Д. Кенигом.
Слайд 3В 1905 году был построен Императорский мост, кото-рый был впоследствии
разрушен в ходе бомбарди-ровки во время Второй мировой войны. На
опорах Императорского моста в 2005 году был построен Юбилейный мост. На 2016 год в Калининграде восемь мостов.
Следующий импульс теория графов получила спустя почти 100 лет с развитием исследований по электри-ческим сетям (Кирхгоф), кристаллографии, органи-ческой химии (Кэли), психологии (Левин) и другим наукам.
С графами, сами того не замечая, мы сталкиваемся постоянно. Например, графом является схема линий метрополитена. Исследуя свою родословную и возводя ее к далекому предку, мы строим так называемое генеалогическое древо.
Слайд 4Элементы теории графов
Под графом G(X,U) понимают совокупность непустого множества X
и подмножества U, представляющего собой множество всех упорядоченных пар (xi,
xj), где xi, xjX. Элементы множеств X и U называют, соответственно, вершинами и дугами (ребрами) графа.
Неориентированный граф (неограф) — граф, рёбра которого не направлены. Ориентированный граф (орграф) — граф, рёбрам которого присвоено направ-ление. Направленные рёбра именуются дугами.
Две вершины xi, xjX считаются смежными, если они определяют ребро (дугу) и, соответственно, два различных ребра (дуги) смежны, если они имеют общую вершину.
Слайд 5Вершина xi инцидента ребру (дуге) uj если она является началом
или концом ребра (дуги). Аналогично утверждение, что ребро (дуга) uj
инцидентно вершине xi, если оно входит или выходит из этой вершины.
Число ребер (дуг), инцидентных некоторой вершине xi, называют локальной степенью вершины и обозначают (xi).
Учитывая, что каждое ребро неориентирован-ного графа инцидентно двум вершинам, полу-чим выражение, связывающее число ребер графа со степенями вершин
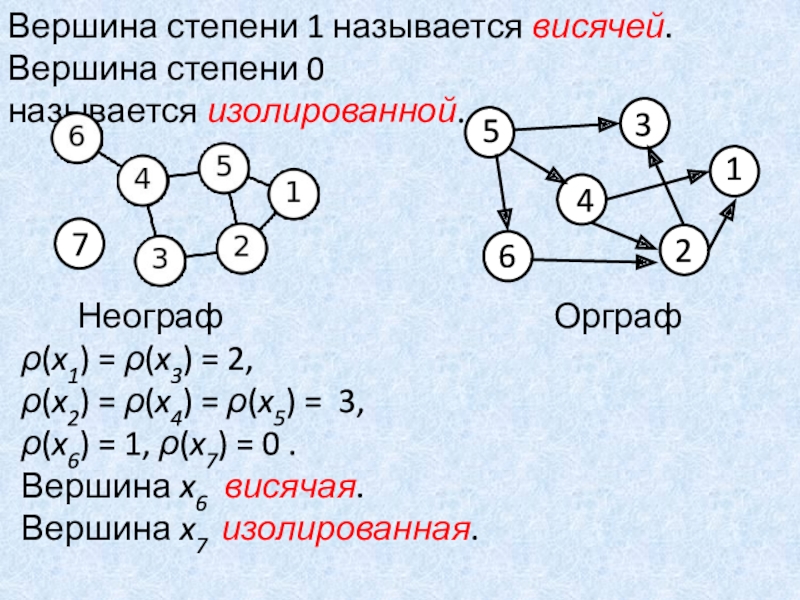
Слайд 6Вершина степени 1 называется висячей. Вершина степени 0 называется изолированной.
7
Неограф
Орграф
(x1) = (x3) = 2,
(x2) = (x4) = (x5) = 3,
(x6) = 1, (x7) = 0 .
Вершина x6 висячая.
Вершина x7 изолированная.
6
5
4
3
2
1
Слайд 7Граф называется простым, если любые две его вершины соединены не
более чем одним ребром, и каждое ребро соединяет различные вершины.
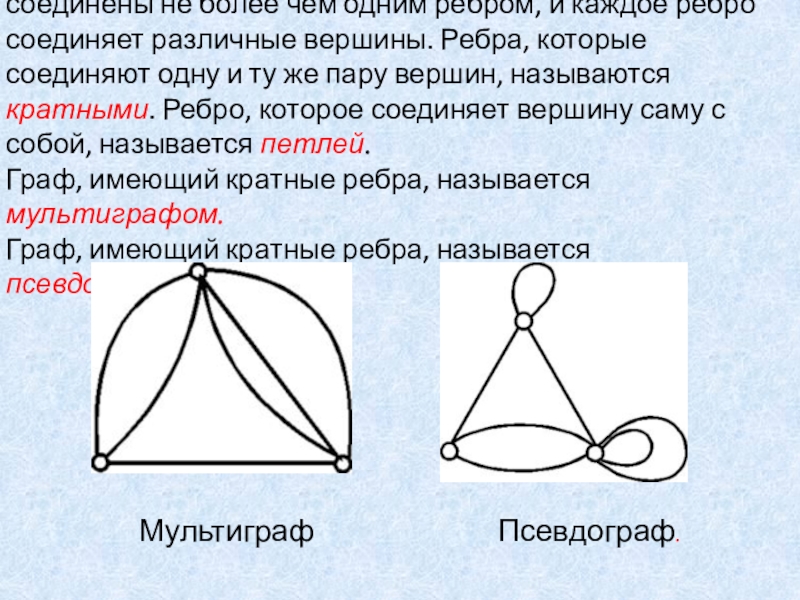
Ребра, которые соединяют одну и ту же пару вершин, называются кратными. Ребро, которое соединяет вершину саму с собой, называется петлей.
Граф, имеющий кратные ребра, называется мультиграфом.
Граф, имеющий кратные ребра, называется псевдографом.
Мультиграф Псевдограф.
Слайд 8Граф, любая пара вершин которого связана, называют связным графом. В
связном графе, перемещаясь по ребрам из вершины в вершину, можно
попасть в каждую вершину. Граф, состоящий из отдельных фрагментов, называют несвязным, состоящим из отдельных компонент связности.
Последовательность ребер ukU заданных парами вершин вида (x0, x1) (x1, x2)...(xl-1, xl), в которой любые два соседних ребра смежные, называется маршрутом.
Число ребер в маршруте определяет его длину. Если все ребра в маршруте различны, то такой маршрут является цепью.
Если в цепи нет повторяющихся вершин, кроме соседних, то такая цепь называется простой.
Слайд 9Циклом называют последовательность ребер u1=(x1, xi), ..., uk=(xj, x1), при
которой в результате обхода вершин графа по этим ребрам возвращаются
в исходную вершину x1.
Каждое ребро графа встречается в цикле не более одного раза, в то время как вершины могут повторяться и несколько раз.
Цикл считают простым, если в нем нет повторяющихся вершин, и сложным, если такие имеются.
Слайд 10Большое значение в задачах конструкторского проектирования ЭВМ имеют эйлеровы и
гамильтоновы циклы.
Эйлеров цикл – это цикл, в котором содержатся все
ребра графа.
Граф, имеющий такой цикл, называют эйлеровым графом. На рисунке изображен граф «Сабли Магомета». Это эйлеров граф, эйлеров цикл х1 х6 х9 х10 х11 х7 х4 х2 х6 х8 х9 х3 х10 х7 х5 х4 х3 х2 х1.
Слайд 11Необходимым и достаточным условием наличия в конечном связном графе эйлерова
цикла является четность степеней всех его вершин (теорема Эйлера).
Цикл называют
гамильтоновым, если он проходит через каждую вершину один раз.
Известно (теорема Оре – Дирака), что граф имеет гамильтонов цикл, если сумма локальных степеней двух любых вершин графа больше или равна числу вершин графа, т.е. xi xjX [(xi) + (xj) n].
Из теоремы следует результат Дирака: граф имеет гамильтонов цикл, если степени любых его вершин xi, xjX [(xi) n/2].
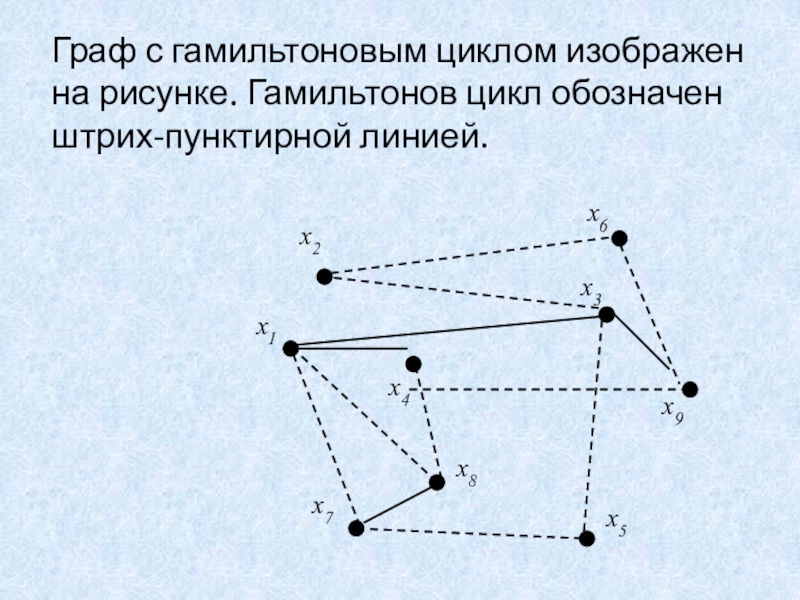
Слайд 12Граф с гамильтоновым циклом изображен на рисунке. Гамильтонов цикл обозначен
штрих-пунктирной линией.
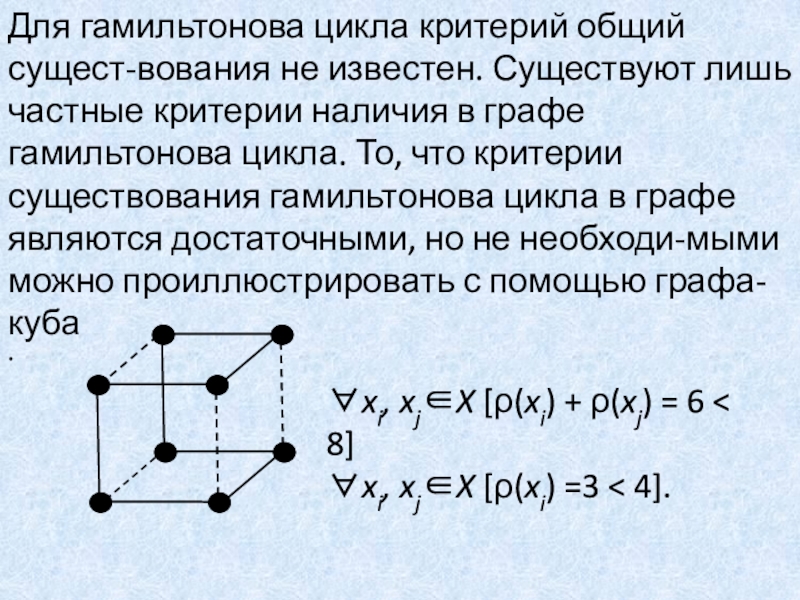
Слайд 13Для гамильтонова цикла критерий общий сущест-вования не известен. Существуют лишь
частные критерии наличия в графе гамильтонова цикла. То, что критерии
существования гамильтонова цикла в графе являются достаточными, но не необходи-мыми можно проиллюстрировать с помощью графа-куба
xi, xjX [(xi) + (xj) = 6 < 8]
xi, xjX [(xi) =3 < 4].
.
Слайд 14При размещении графа в виде геометрической фигуры существует большая свобода
в размещении вершин графа в пространстве и выборе формы соединяющих
их ребер (дуг). Следовательно, один и тот же граф может иметь различную геометрическую реализацию
Два графа G и G’ изоморфны, если они имеют одинаковое число вершин и если каждой паре вершин, соединенных ребром (дугой), в одном графе, соответствует такая же пара вершин, соединенных ребром (дугой), в другом графе.
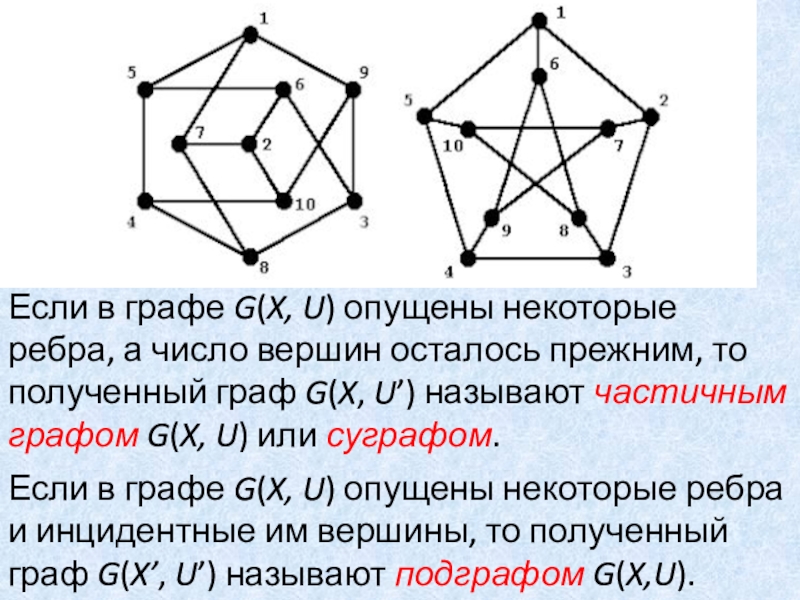
Слайд 15Если в графе G(X, U) опущены некоторые ребра, а число
вершин осталось прежним, то полученный граф G(X, U’) называют частичным
графом G(X, U) или суграфом.
Если в графе G(X, U) опущены некоторые ребра и инцидентные им вершины, то полученный граф G(X’, U’) называют подграфом G(X,U).
Слайд 16Связный неориентированный граф, не содержа-щий циклов, называют деревом и обозначается
T(X, W). Число ребер дерева W = n - 1.
Несвязный
граф без циклов, отдельные компоненты связности которого являются деревьями, называют лесом. Число ребер леса с p компонентами связности W = n - p.
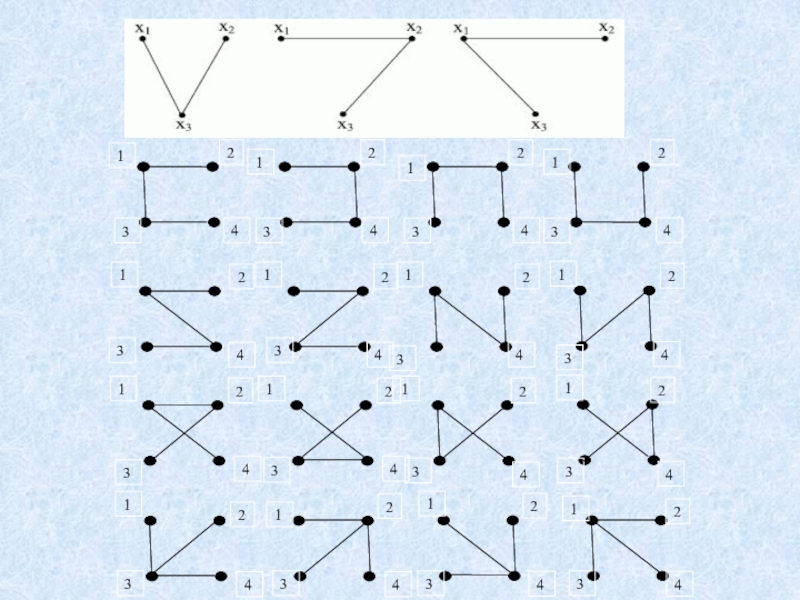
На n вершинах, пронумерованных числами от 1 до n, можно построить nn-2 различных деревьев (теорема Кэли). Таким образом, для n = 3 можно построить ровно три дерева, для n = 4 – 16 деревьев, для n = 5 – 125 деревьев и так далее.
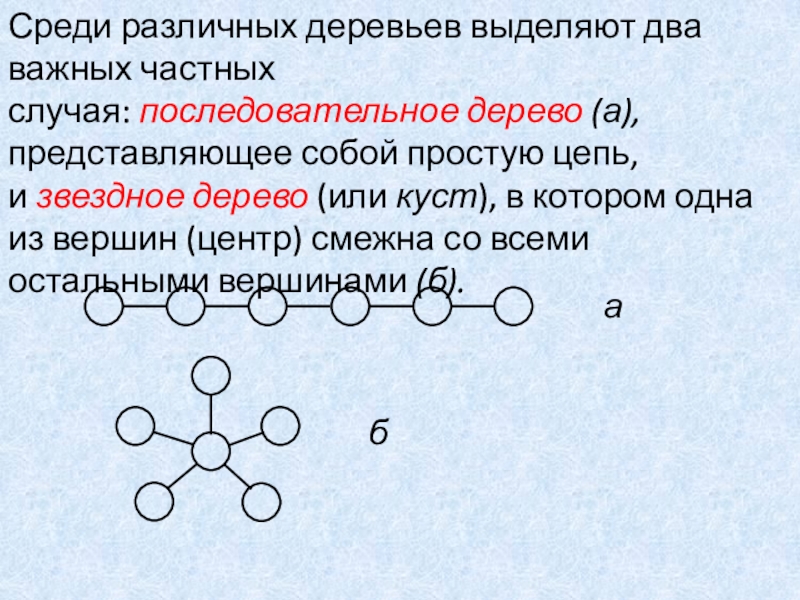
Слайд 18Среди различных деревьев выделяют два важных частных случая: последовательное дерево (а), представляющее
собой простую цепь, и звездное дерево (или куст), в котором одна из вершин (центр)
смежна со всеми остальными вершинами (б).
а
б
Слайд 19Характеристические числа графов
Рассмотрим некоторые характеристические числа графа, не зависящие от
изоморфных преобразований. Такие числа называют инвариантами графа, т.е. у изоморфных
графов они равны.
Цикломатическое число. Цикломатическое число графа указывает то число ребер, которое нужно удалить из данного графа, чтобы получить дерево (для связного графа) или лес (для несвязного графа), т.е. добиться отсутствия у графа циклов.
Пусть связный граф G(X, U) имеет n=X вершин и r=U ребер. Тогда, дерево, построенное на этом графе имеет W = n-1 ребро. По определению цикломатическое число
(G) = r - (n -1) = r – n +1.
Слайд 20Для несвязного графа с p компонентами связности, цикломатическое число
(G)
= r – n + p.
Цикломатическое число всегда неотрицательно.
Цикломатическое число
графа равно максимальному числу независимых циклов.
Хроматическое число. Пусть, задан граф G(X,U) без петель. Разобьем множество его вершин на k непересекающихся подмножеств X1, X2, ..., Xk,
] так, чтобы любые две смежные вершины xa и xbX принадлежали разным подмножествам, т.е. чтобы ребра графа G(X,U) соединяли вершины из разных подмножеств (XsX [ГXsXs=], где ГXs множество вершин, смежных вершинам множества Xs).
Слайд 21Задача раскраски вершин графа формулируется следующим образом. Необходимо раскрасить вершины
графа таким образом, чтобы смежные вершины были окрашены в разные
цвета. Минимальное число красок, в которые можно раскрасить граф называется хроматическим числом графа и обозначается (G), а граф G(X, U) называют -хроматическим.
Особое значение имеет частный вид -хроматичес-кого графа – бихроматический граф, для которого множество вершин X можно разбить на два непересекающихся подмножества Х1 и Х2 так, чтобы ребра соединяли вершины разных подмножеств (Х=Х1Х2, Х1Х2=, хiX1 [ГxiX1=], хjX2 [ГxjX2=].
Слайд 22Такие графы называют бихроматическими, двудольными графами или графами Кенига и
обозначают G(X1, Х2, U).
В отличие от цикломатического числа определение хроматического
числа осуществляется с помощью сравнительно сложных алгоритмов, в основу большинства которых положены методы целочисленного линейного программирования.
Число планарности. Граф G(X, U) называют плоским тогда и только тогда, когда он геометрически реализован на плоскости так, что все его ребра пересекаются только в вершинах Х графа. Граф G(X,U) называют планарным, если он может быть геометрически реализован на плоскости без пересечения ребер.
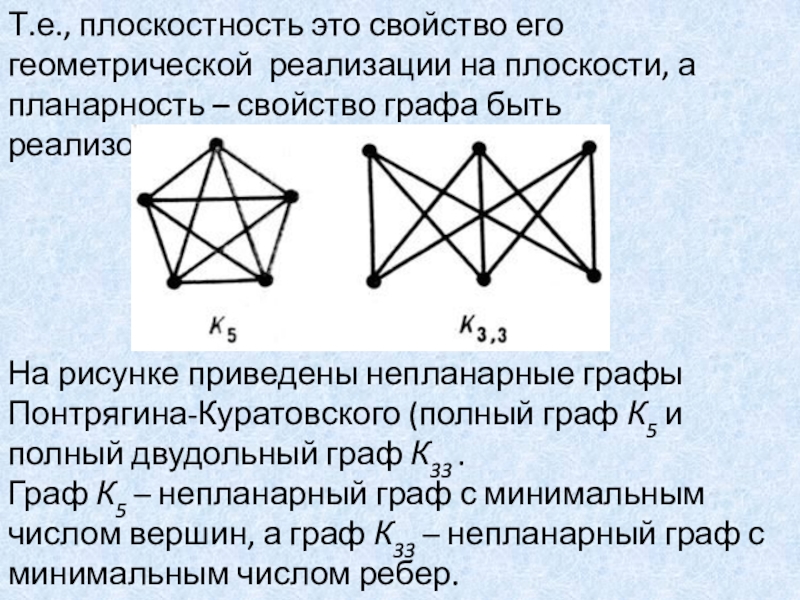
Слайд 23Т.е., плоскостность это свойство его геометрической реализации на плоскости, а
планарность – свойство графа быть реализованным на плоскости.
На рисунке
приведены непланарные графы Понтрягина-Куратовского (полный граф К5 и полный двудольный граф К33 .
Граф К5 – непланарный граф с минимальным числом вершин, а граф К33 – непланарный граф с минимальным числом ребер.
Слайд 24Минимальное число ребер, которое нужно удалить из графа, чтобы он
стал планарным, называется числом планарности и обозначается (G). Для полного
графа Кn с n ≥4
(G) = (n - 3)(n - 4)/2.
Минимальное число плоских суграфов, на которые разбивается граф G(X,U) называется толщиной графа t(G).
В 1976 г. американские математики К. Аппель и В. Хейкен доказали гипотезу четырех красок, существенно используя при этом компьютерные вычисления.
Слайд 25Число внутренней устойчивости. Множество вершин Хs графа G(X,U) называется внутренне
устойчивым (независимым), если никакие две вершины из этого множества не
смежны, XsX [ГXsXs=]. Внутренне устойчивое множество называется максимальным, если оно не является собственным подмножеством некоторого другого независимого множества. Максимальное по мощности независимое множество называется наибольшим. Число вершин в наибольшем независимом множестве графа G(X,U) называется числом внутренней устойчивости этого графа и обозначается (G), (G)=maxXs.
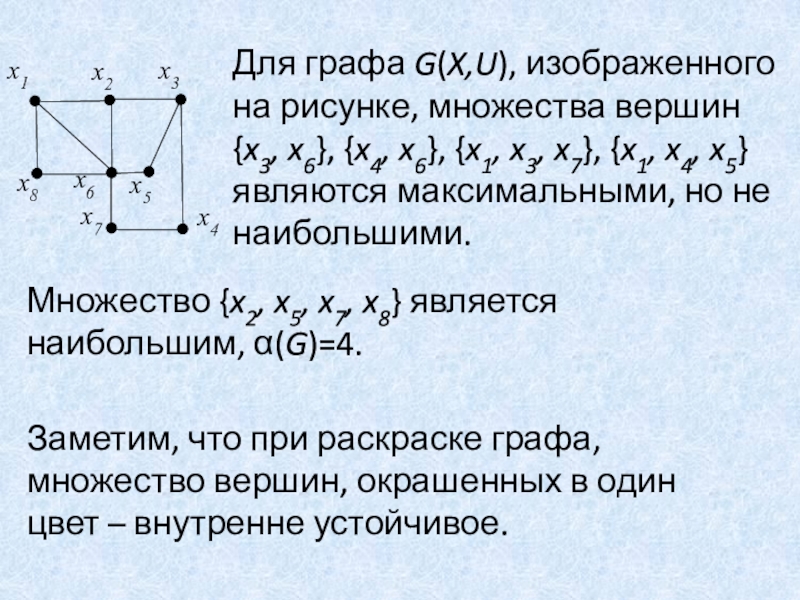
Слайд 26Для графа G(X,U), изображенного на рисунке, множества вершин {x3, x6},
{x4, x6}, {x1, x3, x7}, {x1, x4, x5} являются максимальными,
но не наибольшими.
Множество {x2, x5, x7, x8} является наибольшим, (G)=4.
Заметим, что при раскраске графа, множество вершин, окрашенных в один цвет – внутренне устойчивое.
Слайд 27Число внешней устойчивости. Множество вершин Хs графа G (X,U) называется
внешне устойчивым (доминирующим), если каждая вершина из X\Xs смежна с
некоторой вершиной из Xs. Иначе говоря, каждая вершина графа xjXs или xjГXs, т.е. находится на расстоянии не более 1 от внешне устойчивого множества, ГXsXs=Х.
Число вершин в наименьшем независимом множестве графа G (X,U) называется числом внешней устойчивости этого графа и обозначается (G), (G) = minXs.
Внешне устойчивое множество Xs называется минимальным, если при удалении из него любой вершины получается множество, не являющееся внешне устойчивым.
Слайд 28Для графа G (X,U), изображенного на рисунке, множества вершин {x1,
x3, x7}, {x2, x4, x5, x8} являются минимальными, но не
наименьшими.
Множества {x3, x6} и {x4, x6} является наименьшими, (G)=2.
Подмножество вершин графа, являющееся как внутренне устойчивым, так и внешне устойчивым, называется ядром.
Внешне устойчивое множество, состоящее из минимального числа вершин, называется наименьшим.
Слайд 29Плотность графа. Максимальный полный подграф графа G (X,U) называется кликой
графа G; другими словами, клика графа G есть подмножество его
вершин, такое, что между каждой парой вершин этого подмножества существует ребро и, кроме того, это подмножество не принадлежит никакому большому подмножеству с тем же свойством.
Число вершин клики графа называется плотностью графа и обозначается f(G).
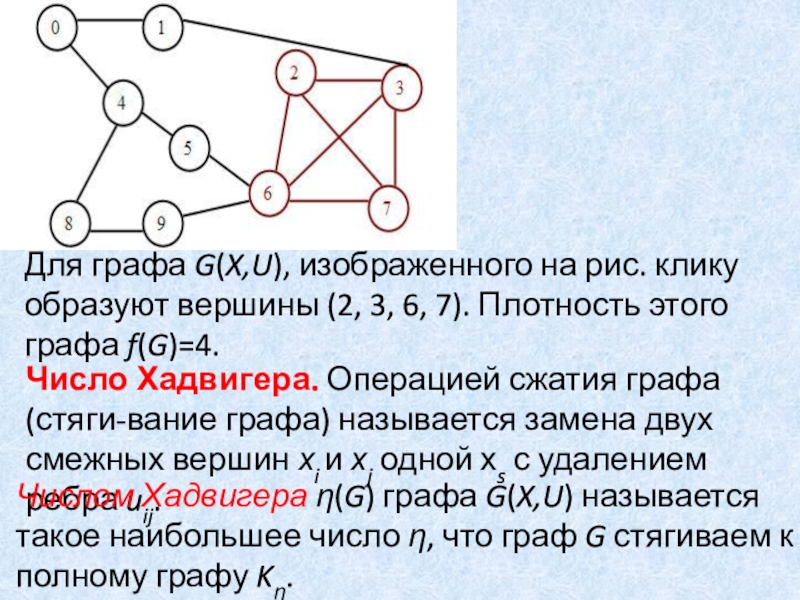
Слайд 30Для графа G(X,U), изображенного на рис. клику образуют вершины (2,
3, 6, 7). Плотность этого графа f(G)=4.
Число Хадвигера. Операцией сжатия
графа (стяги-вание графа) называется замена двух смежных вершин хi и хj одной хs с удалением ребра uij.
Числом Хадвигера (G) графа G(X,U) называется такое наибольшее число , что граф G стягиваем к полному графу K.
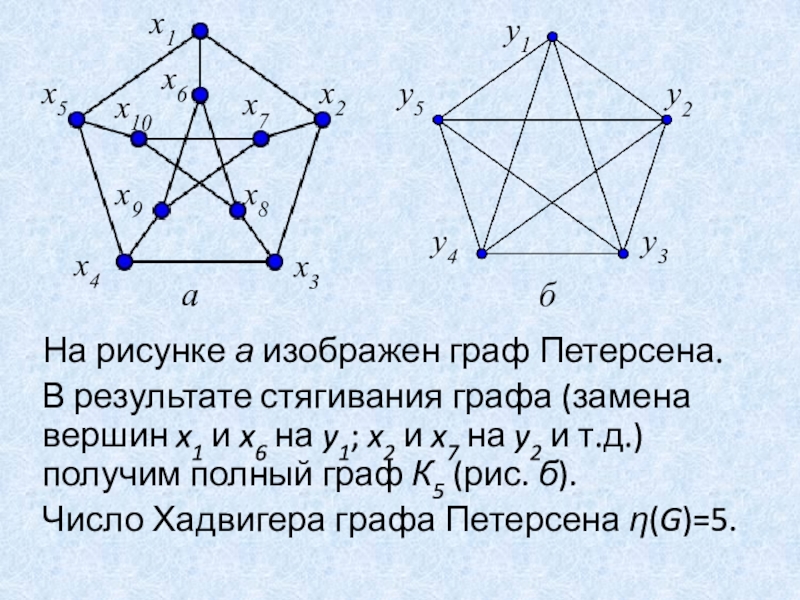
Слайд 31На рисунке а изображен граф Петерсена.
В результате стягивания графа (замена
вершин x1 и x6 на y1; x2 и x7 на
y2 и т.д.) получим полный граф К5 (рис. б).
Число Хадвигера графа Петерсена (G)=5.
б
а
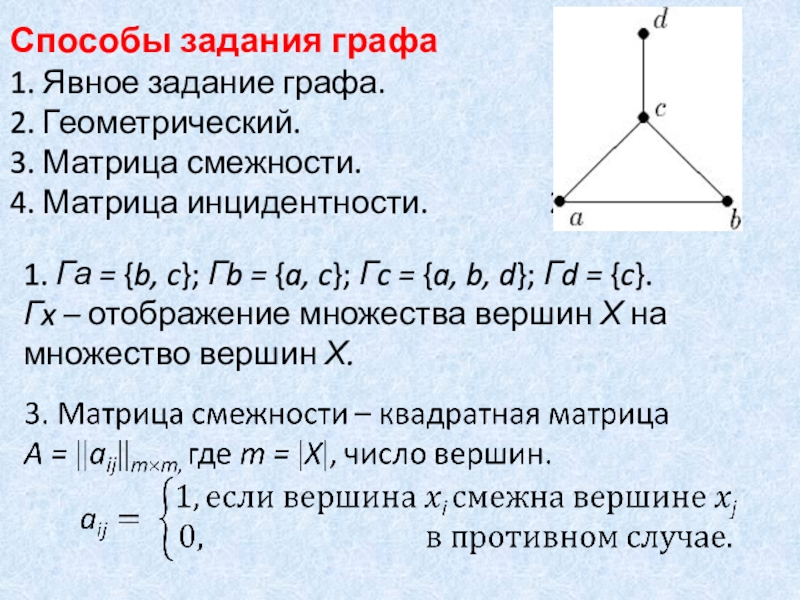
Слайд 32Способы задания графа
1. Явное задание графа.
2. Геометрический.
3. Матрица смежности.
4. Матрица
инцидентности. 2.
1. Га
= {b, c}; Гb = {a, c}; Гc = {a, b, d}; Гd = {c}.
Гx – отображение множества вершин Х на множество вершин Х.
Слайд 34Основные задачи теории графов
1. Независимые и доминирующие множества.
Независимое множество (внутренне
устойчивое мно-жество) есть множество вершин графа G(X,U), такое, что любые
две вершины в нем не смежны. Следовательно, любое множество S X, которое удовлетворяет условию S Г(S)=, является независимым множеством вершин.
Выбор проекта.
Имеется n проектов, которые должны быть выполнены, и для выполнения проекта xi требуется некоторое мно-жество Ri наличных ресурсов из множества {1, …, p}. Построим граф G, каждая вершина которого соответ-ствует некоторому проекту, ребро (xi , xj) – наличию общих средств обеспечения у проектов xi и xj, т.е.
Ri Rj .
Слайд 35Максимальное независимое множество графа G представляет максимальное множество проектов, которое
можно выполнить одновременно за один и тот же промежуток времени.
2.
Доминирующие множества
Доминирующее множество вершин графа G(X,U) (внешне устойчивое множество) есть множество вершин S X, такое, что для каждой вершины xj, не входящей в S, существует ребро, соединяющее некоторую вершину из S с вершиной xj. Следовательно, S есть доминирующее множество, если S Г(S)=Х
Слайд 36Размещение «центров», покрывающих заданную область
(а) Размещение телевизионных или радиопередающих станций
на некоторой территории;
(б) Размещение военных баз, контролирующих данную территорию;
(в) Размещение
центров торговли, обслуживающих некоторый район.
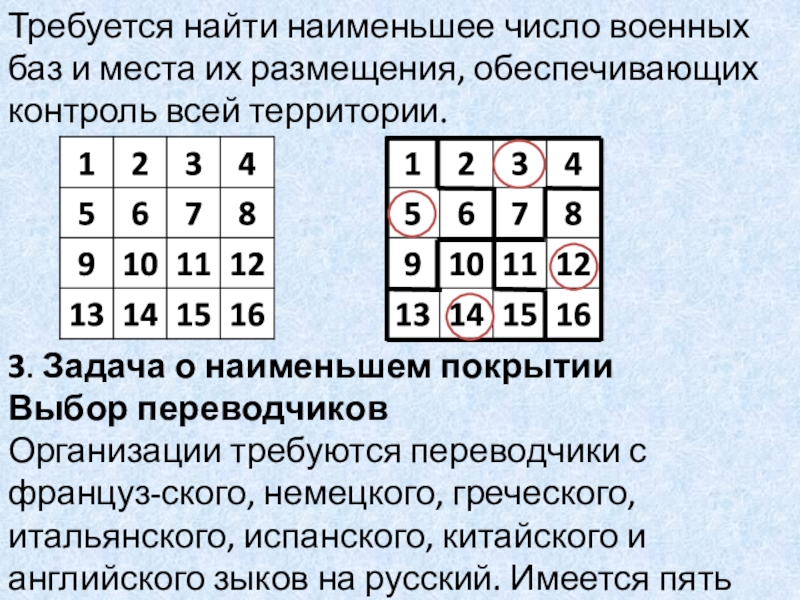
Предположим, что территория, представленная большим квадратом, разделена на 16 районов. Военная база, расположенная в каком-либо районе может контролировать этот район и соседние, граничащие с ним районы.
Слайд 37Требуется найти наименьшее число военных баз и места их размещения,
обеспечивающих контроль всей территории.
3. Задача о наименьшем покрытии
Выбор переводчиков
Организации требуются
переводчики с француз-ского, немецкого, греческого, итальянского, испанского, китайского и английского зыков на русский. Имеется пять кандидатур A, B, C, D и E.
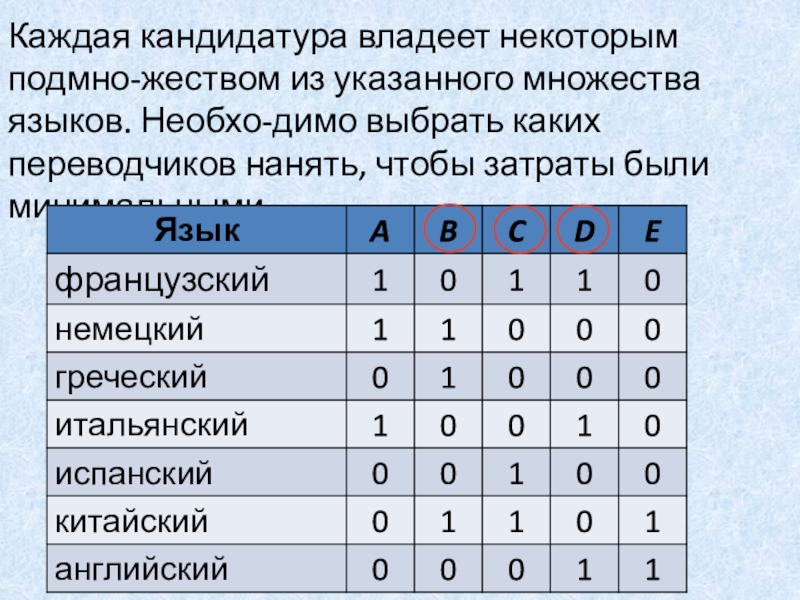
Слайд 38Каждая кандидатура владеет некоторым подмно-жеством из указанного множества языков. Необхо-димо
выбрать каких переводчиков нанять, чтобы затраты были минимальными.
Слайд 393. Раскраски
Граф G называется r-хроматическим, если его вершины могут быть
раскрашены с использова-нием r цветов (красок) так, что не найдется
двух смежных вершин одного цвета. Наименьшее число r, такое, что граф G является r-хроматичес-ким, называется хроматическим числом графа. Задача нахождения хроматического числа назы-вается задачей раскраски графа. Раскраска разби-вает множество вершин графа на r независимых подмножеств, каждое из которых содержит вершины одного цвета.
Эта задача явилась предметом многих исследо-ваний в конце XIX и в ХХ веках.
Слайд 40Гипотеза четырех красок.
Задача заключается в том, чтобы раскрасить географи-ческую карту
так, чтобы пограничные страны были окрашены в разные цвета (не
пограничные страны можно окрашивать одним цветом), использовав при этом наименьшее число красок. В 1850 г. Фрэнсис Гутри, раскрасив карту графств Англии четырьмя цве-тами, выдвинул гипотезу о том, что этого количества цветов достаточно для раскраски любой карты. Он привлек к проблеме внимание своего преподавателя математики А. Де Моргана, а тот сообщил о ней сво-ему другу сэру В. Гамильтону (письмо датировано 23.10.1852) и тем самым способствовал ее широкому распространению.
Слайд 41В 1890 году английский математик П. Хивуд доказал, что любую
карту на плоскости можно раскрасить в пять цветов.
В 1976 г.
математики из Иллинойского университета Кеннет Аппель и Вольфганг Хакен с помощью ЭВМ создали 1936 карт, ни одна из которых не могла опровергнуть верность теории. Доказательство заняло сотни листов. На его основании ученые утверждали, что контрпримера этой теореме существовать не может!
Слайд 42Задача размещения
Необходимо разместить n каких-то предметов по ящикам. Строим граф
G в котором каждой вершине соответствует предмет. Ребро между вершинами
xi и xj вводится, если эти два предмета не могут быть помещены в один ящик. Если ящики имеют неограниченную вместимость, то зада-ча нахождения наименьшего числа ящиков сводится к определению хроматического числа графа G.
Составление графиков осмотров
В задачах теории расписаний осмотры представляются временными интервалами. Каждому осмотру сопоставля-ется вершина графа. Две вершины соединяются ребром, тогда, когда осмотры нельзя проводить одновременно. Требуется составить график осмотров с минимальными временными затратами. Задача сводится к раскраске графа в минимальное число цветов.
Слайд 434. Размещение центров
В практической деятельности постоянно возникают задачи «наилучшего» размещения
оборудования в сетях или графах. В частности, если граф представляет
сеть дорог и вершины соответствуют отдельным районам, то можно поставить задачу оптимального размещения больниц, полицейских участков, пожарных частей и других предприятий и служб. Критерий оптимальности может состоять в минимизации расстояния (или времени проезда) от пункта обслуживания до самой отдаленной вершины графа, т.е. в оптимизации «наихудшего варианта». Задачи такого типа называются минимаксными задачами размещения. Полученные при решении места размещения называются центрами графа.
Слайд 44В других задачах необходимо минимизировать сумму всех расстояний от вершин
графа до центра обслуживания (размещение склада в сети дорог, размещение
телефон-ных станций в телефонной сети). Такие задачи называются минисуммными задачами размещения. Места размеще-ния, полученные в результате решения минисуммных задач, называются медианами графа.
Слайд 455. Деревья
Одно из наиболее важных понятий теории графов.
Остовное дерево — ациклический связный
подграф данного связного неографа, в который входят все его вершины.
Минимальное остовное дерево (SST - shortest spanning tree) в связанном взвешенном графе — это остовное дерево этого графа, имеющее минимальный возможный вес, где под весом дерева понимается сумма весов входящих в него рёбер.
Задачи о кратчайших расстояниях на графах:
Построение минимального остовного дерева (кратчайшей связывающей сети) – соединение всех узлов сети с помощью путей наименьшей длины.
Задача о нахождении дерева кратчайших расстояний – нахождение кратчайшего пути из одной вершины в любую другую.
Слайд 46Необходимо проложить линии коммуникаций (дороги, линии связи, электропередач и т.п.)
между n заданными "точечными" объектами, при условии, что известны "расстояния"
между каждой парой объектов (это может быть геометрическое расстояние или стоимость прокладки коммуникаций между ними).
Необходимо добраться на самолете из города A в город B при условии, что между ними нет прямого авиационного сообщения, затратив при этом минимальные средства (при условии, что заданы возможные промежуточные аэропорты, для каждой пары аэропортов известно, существует ли между ними прямой маршрут, и если да, то известна минимальная стоимость перелета по этому маршруту).
Слайд 47Задача Штейнера
В задаче определения SST ребрами покрывались все вершины множества
Х. В практике встречаются задачи, в которых разрешается вводить дополнительные
вершины и соединяющие их ребер (соединения «контакт» - «проводник», «проводник» - «проводник»).
Такая задача называется задачей Штейнера, деревья соединений – деревьями Штейнера (ДШ), а дополни-тельные вершины – точками Штейнера (ТШ).
Задача построения дерева Штейнера имеет следующий вид. Требуется найти такой связный ациклический граф с использованием дополнительных вершин Штейнера (дерево Штейнера) Т’ = (Х’,U’), что Х’ включает все вершины Х и дополнительные вершины (точки Штейнера) и суммарный вес ребер в T’ будет минимальным.
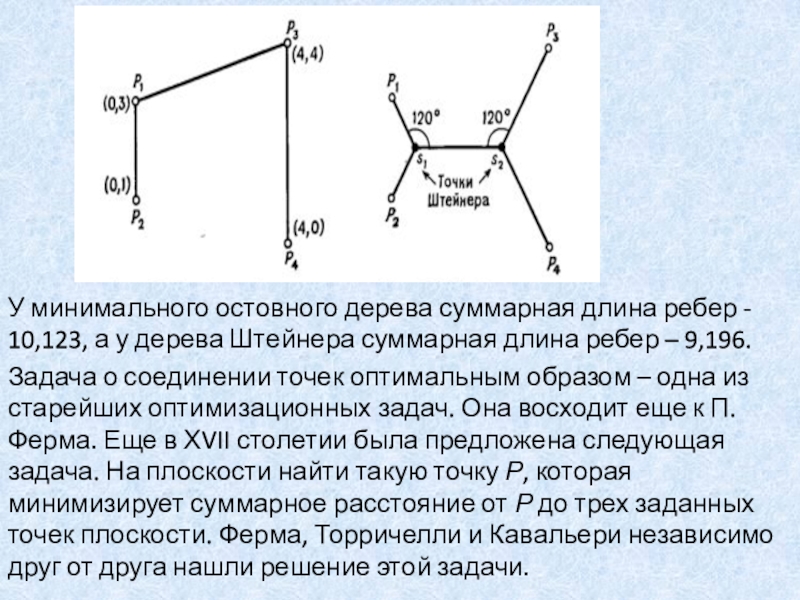
Слайд 48У минимального остовного дерева суммарная длина ребер - 10,123, а
у дерева Штейнера суммарная длина ребер – 9,196.
Задача о соединении
точек оптимальным образом – одна из старейших оптимизационных задач. Она восходит еще к П. Ферма. Еще в ХVII столетии была предложена следующая задача. На плоскости найти такую точку Р, которая минимизирует суммарное расстояние от Р до трех заданных точек плоскости. Ферма, Торричелли и Кавальери независимо друг от друга нашли решение этой задачи.
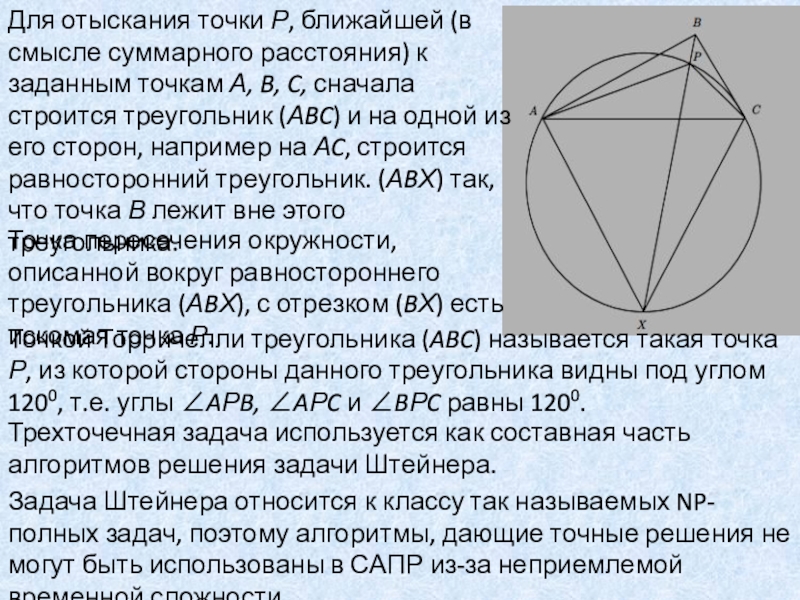
Слайд 49Для отыскания точки Р, ближайшей (в смысле суммарного расстояния) к
заданным точкам А, B, C, сначала строится треугольник (АBC) и
на одной из его сторон, например на АC, строится равносторонний треугольник. (АBХ) так, что точка В лежит вне этого треугольника.
Точка пересечения окружности, описанной вокруг равностороннего треугольника (АBХ), с отрезком (BХ) есть искомая точка Р.
Точкой Торричелли треугольника (ABC) называется такая точка Р, из которой стороны данного треугольника видны под углом 1200, т.е. углы AРB, AРC и BРC равны 1200.
Трехточечная задача используется как составная часть алгоритмов решения задачи Штейнера.
Задача Штейнера относится к классу так называемых NP-полных задач, поэтому алгоритмы, дающие точные решения не могут быть использованы в САПР из-за неприемлемой временной сложности.
Слайд 506. Кратчайшие пути
Пусть дан граф G(X, Γ), ребрам которого приписаны
веса (стоимости), заданные матрицей C=cijm×m.
Задача о кратчайшем пути состоит
в нахождении пути с минимальным суммарным весом от начальной вершины sX до конечной tX или от начальной вершины sX до всех остальных, при условии, что такие пути существуют.
Задачи, близкие к задаче о кратчайшем пути
1. Наиболее надежный путь.
В этом случае вес ребра представляет его надежность. Надежность пути от s к t, составленного из ребер, взятых из множества P, задается формулой
где ρij – надежность ребра (xi, xj).
Слайд 512. Самый длинный (критический) путь.
Задача сетевого планирования, заключающаяся в нахождении
самого длинного по временной протяженности пути в сетевом графике, определяющего
продолжительность работ по выполнению проекта.
3. Путь с наибольшей пропускной способностью.
В этом случае каждое ребро графа имеет пропускную способность qij и требуется найти путь от s к t с наибольшей пропускной способностью. Пропускная способность пути P определяется ребром из P с наименьшей пропускной способностью, т.е.
Слайд 527. Эйлеровы циклы и задача китайского почтальона
Ребрам графа G приписаны
положительные веса. Требу-ется найти цикл, проходящий через каждое ребро графа
G по крайней мере один раз и такой, что для него общий вес (а именно сумма njc(aj), где число nj показывает, сколько раз проходилось ребро аj, а c(aj) – вес ребра) минимален.
Сформулированная выше задача называется задачей китайского почтальона и ее решение имеет много потенциальных приложений:
а) Сбор мусора.
б) Доставка молока и почты.
в) Проверка электрических, телефонных или железнодорожных линий.
г) разбрасывание смеси песка и соли на главных дорогах зимой для предотвращения обледенения.
Слайд 53д) наилучший метод работы автоматических вентиляционных устройств.
е) уборка помещений и
коридоров в больших учреждениях.
ж) наилучший маршрут осмотра музея!
8. Гамильтоновы
циклы и задача коммивояжера
В ряде отраслей промышленности, особенно химической и фармацевтической, возникает следующая основная задача планирования. Нужно произвести n продуктов, используя единственный тип аппаратуры. Аппарат дол-жен или не должен быть перенастроен после того как произведен продукт pi до того, как началось производ-ство продукта рj, в зависимости от комбинации (pi , рj). Стоимость перенастройки аппаратуры постоянна и не зависит от продукта, который был произведен и который будет произведен.
Слайд 54Задача коммивояжера
В задаче коммивояжера рассматривается n городов и
матрица попарных расстояний между ними. Требуется
найти такой порядок посещения городов, чтобы сум-марное пройденное расстояние было минимальным,
каждый город посещался ровно один раз и коммивояжер вернулся в тот город, с которого
начал свой маршрут. Другими словами, во взвешенном полном графе требуется найти гамильтонов цикл
минимального веса. Простота формулировки, конечность множества допусти-мых решений, наглядность и, в тоже время, колоссаль-ные затраты на полный перебор до сих пор подталкиваютматематиков к разработке все новых и новых численных методов.
Слайд 559. Паросочетания, транспортная задача
Слайд 56Возникает вопрос о том, может ли быть найдена циклическая последовательность
производства продуктов рi (i = 1, 2, …, n), не
требующая перенастройки аппаратуры. Ответ зависит от того, имеет граф гамильтонов цикл или нет.
Если не существует циклической последовательности про-дуктов, не требующей перенастройки аппаратуры, то ка-кова должна быть последовательность производства с наименьшими затратами на перенастройку, т. е. требу-ющая наименьшего числа необходимых перенастроек?
Ответ на этот вопрос может быть получен с помощью итеративного применения алгоритма нахождения гамильтонова цикла в графе.
Слайд 57Задача размещения по критерию СДС состоит в минимизации функционала F(P)
на множестве перестановок Р. Данная задача называется задачей квадратичного назначения.
Для решения этой задачи предложен ряд алгоритмов, основанных на методе ветвей и границ.
Метод ветвей и границ
Основная идея метода заключается в разбиении всего множества допустимых решений на подмножества и просмотра каждого под-множества с целью выбора оптимального. Для всех решений вы-числяется нижняя граница минимального значения целевой функ-ции. Как только нижняя граница становится больше значения целе-вой функции для наилучшего из ранее известных, подмножество решений, соответствующее этой границе исключается из области решений. Это обеспечивает сокращение перебора.
Поиск продолжается до тех пор, пока не будут исключены все решения, кроме оптимального.
Слайд 58Различные модификации общего метода отличаются способом расчета нижних границ и
способом разбиения поля решений.
Для описания процесса поиска оптимального размещения строится
дерево решений. Ребра первого яруса дерева соответствуют назначениям элемента е1 в позиции, второго – е2 и т. д. Произвольному размещению элементов соответствует в дереве решений некоторый путь, исходящий из начальной вершины.
Для каждой вершины дерева можно рассчитать нижнюю границу целевой функции для множества путей, связанных с этой вершиной. Если эта граница больше значения целевой функции для известного размещения, то дальнейшее продвижение по дереву в этой вершине прекращается.
Для вычисления нижней границы можно воспользоваться следующим свойством: если r = {r1, r2, ..., rm} и d = {d1, d2, ..., dm} два вектора, то минимум скалярного произведения r и d, т. е. минимум на множестве всех перестановок Р, соответствует расположению составляющих вектора r в невозрастающем порядке, а вектора d – в неубывающем.
Слайд 59Таким образом, простейшая нижняя граница может быть получена при рассмотрении
верхних половин матриц R и D в качестве составляющих векторов
r и d длиной m(m-1) / 2 и при выполнении указанного выше упорядочивания.
Пусть имеется некоторое частичное размещение q множества элементов Ek на множестве позиций Pk. Тогда нижняя граница складывается из следующих частей
F(P) = F(q) + w(P) + v(P), где
- суммарная длина соединений между
размещенными элементами;
- суммарная длина соединений
между размещенными и неразмещенными элементами;
- суммарная длина соединений между
неразмещенными элементами.
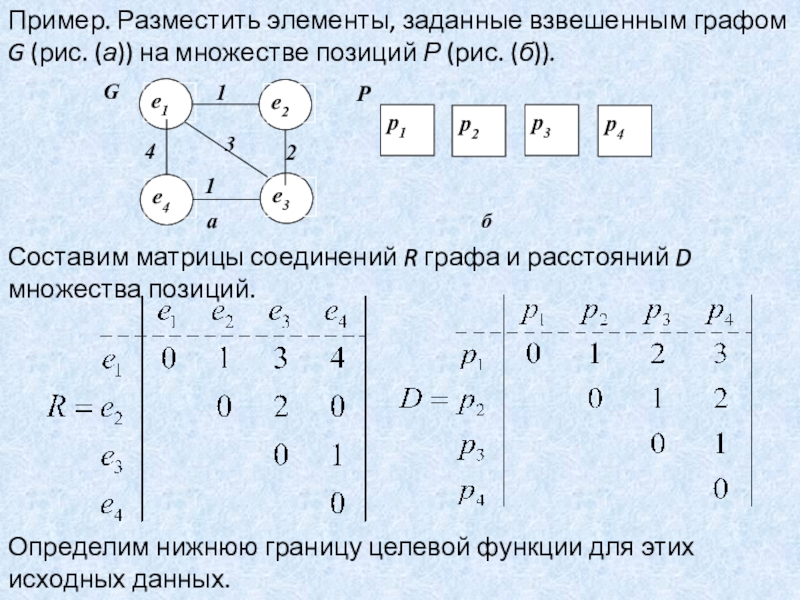
Слайд 60Пример. Разместить элементы, заданные взвешенным графом G (рис. (а)) на
множестве позиций Р (рис. (б)).
Составим матрицы соединений R графа
и расстояний D множества позиций.
Определим нижнюю границу целевой функции для этих исходных данных.
Слайд 61Для этого упорядочим составляющие вектора r в невозрастающем порядке, а
вектора d – в неубывающем.
r = {4
3 2 1 1 0}
d = {1 1 1 2 2 3}
rd = 4 + 3 + 2 + 2 +2 + 0 = 13.
Это значит, что для этих исходных данных значение целевой функции F(P) не может быть меньше 13.
1. Помещаем элемент e1 в позицию р1.
Т. к. размещен один элемент F(q) = 0.
Неразмещенные элементы {e2, e3, e4}, свободные позиции {р2, р3, р4}.
Составим вектор, соответствующий первой строке матрицы R r1 ={4 3 1}, и вектор, соответствующий первой строке матрицы D d1 ={1 2 3}, суммарная длина соединений между размещенным и неразмещенными элементами
w(P) = r1d1 = 4 + 6 + 3 =13.
Для оценки v(P) вычеркнем из матриц R и D первые строки и столбцы и образуем вектора: r ={2 1 0} и d ={1 1 2}, соответствующие верхним половинам усеченных матриц R и D.
Слайд 62Получим v(P) = rd = 2 + 1 + 0
= 3.
Таким образом, нижняя граница F(P) = 0 +
13 + 3 = 16.
2. Помещаем элемент e1 в позицию р2. По-прежнему F(q)=0.
Неразмещенные элементы {e2, e3, e4}, свободные позиции {р1, р3, р4}.
Составим вектор, соответствующий первой строке матрицы
R r1 ={4 3 1}, и вектор, соответствующий второй строке матрицы D
d2 ={1 1 2}, суммарная длина соединений между размещенным и неразмещенными элементами
w(P) = r1d2 = 4 + 3 + 2 = 9.
Для оценки v(P) вычеркнем из матрицы R первые строку и столбец, а из матрицы D вторые строку и столбец. Образуем вектора:
r={2 1 0} и d={1 2 3}, соответствующие верхним половинам усеченных матриц R и D. Получим v(P) = rd = 2 + 2 + 0 = 4. Таким образом, нижняя граница F(P) = 0 + 9 + 4 = 13.
Очевидно, что ввиду симметричности позиций (р1 и р4) и (р2 и р3) будут получены те же результаты для симметричных позиций. На рисунке представлены результаты расчета нижних границ для первого яруса дерева решений.
Слайд 63Назначаем элемент e1 в позицию р2.
3. Помещаем элемент e2 в
позицию р1. Размещены два элемента: e1 в позиции р2 и
e2 в позиции р1, F(q) = r12d21 = 1.
Неразмещенные элементы {e3, e4}, свободные позиции {р3, р4};
r1 ={4 3} и d2={1 2}, r1d2 = 4 + 6 =10;
r2 ={2 0} и d1={2 3}, r2d1 = 4 + 0 = 4;
w(P) = 10 + 4 =14.
r ={1} и d ={1}, v(P) = rd = 1. F(P) = 1 + 14 + 1 = 16.
4. Помещаем элемент e2 в позицию р3. Размещены два элемента: e1 в позиции р2 и e2 в позиции р3, F(q) = r12d23 = 1.
Неразмещенные элементы {e3, e4}, свободные позиции {р1, р4};
r1 ={4 3} и d2 ={1 2}, r1d2 = 4 + 6 = 10;
r2 ={2 0} и d3 ={1 2}, r2d3 = 2 + 0 = 2;
w(P) = 10 + 2 =12.
r = {1} и d ={3}, v(P) = rd = 3. F(P) = 1 + 12 + 3 = 16.
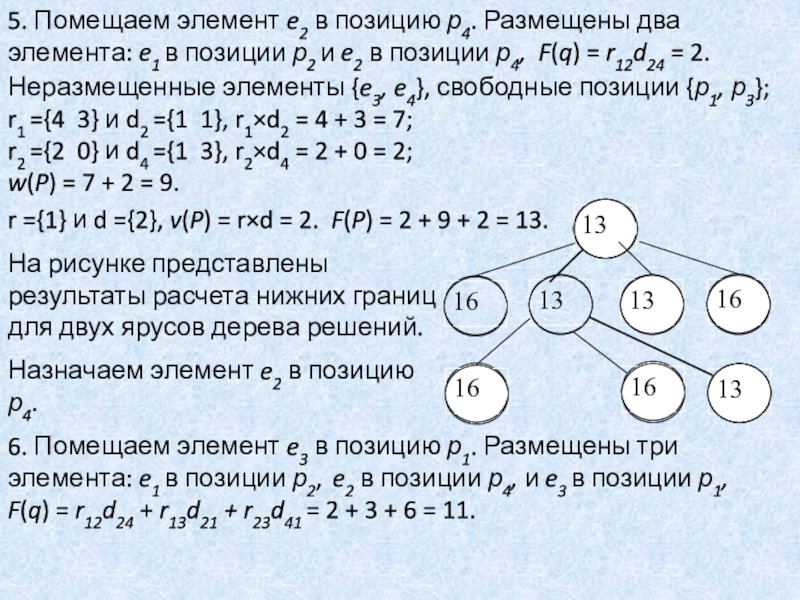
Слайд 645. Помещаем элемент e2 в позицию р4. Размещены два элемента:
e1 в позиции р2 и e2 в позиции р4, F(q)
= r12d24 = 2.
Неразмещенные элементы {e3, e4}, свободные позиции {р1, р3};
r1 ={4 3} и d2 ={1 1}, r1d2 = 4 + 3 = 7;
r2 ={2 0} и d4 ={1 3}, r2d4 = 2 + 0 = 2;
w(P) = 7 + 2 = 9.
r ={1} и d ={2}, v(P) = rd = 2. F(P) = 2 + 9 + 2 = 13.
На рисунке представлены результаты расчета нижних границ для двух ярусов дерева решений.
Назначаем элемент e2 в позицию р4.
6. Помещаем элемент e3 в позицию р1. Размещены три элемента: e1 в позиции р2, e2 в позиции р4, и e3 в позиции р1,
F(q) = r12d24 + r13d21 + r23d41 = 2 + 3 + 6 = 11.
Слайд 65Неразмещенный элемент {e4}, свободная позиция {р3};
r1 ={4} и d 2={1},
r1d2 = 4;
r2 ={0} и d4 ={1}, r2d4 =
0;
r3 ={1} и d1={2}, r2d1 = 2;
w(P) = 4 + 0 + 2 = 6.
Неразмещенный элемент один, v(P) = 0. F(P) = 11 + 6 + 0 = 17.
7. Помещаем элемент e3 в позицию р3. Размещены три элемента: e1 в позиции р2 , e2 в позиции р4, и e3 в позиции р3,
F(q) = r12d24 + r13d23 + r23d43 = 2 + 3 + 2 = 7.
Неразмещенный элемент {e4}, свободная позиция {р1};
r1 ={4} и d2 ={1}, r1d2 = 4;
r2 ={0} и d4 ={1}, r2d4 = 0;
r3 ={1} и d3 ={2}, r2d3 = 2;
w(P) = 4 + 0 + 2 = 6.
Неразмещенный элемент один, v(P) = 0. F(P) = 7 + 6 + 0 = 13.
На рисунке представлены результаты расчета нижних границ для трех ярусов дерева решений.
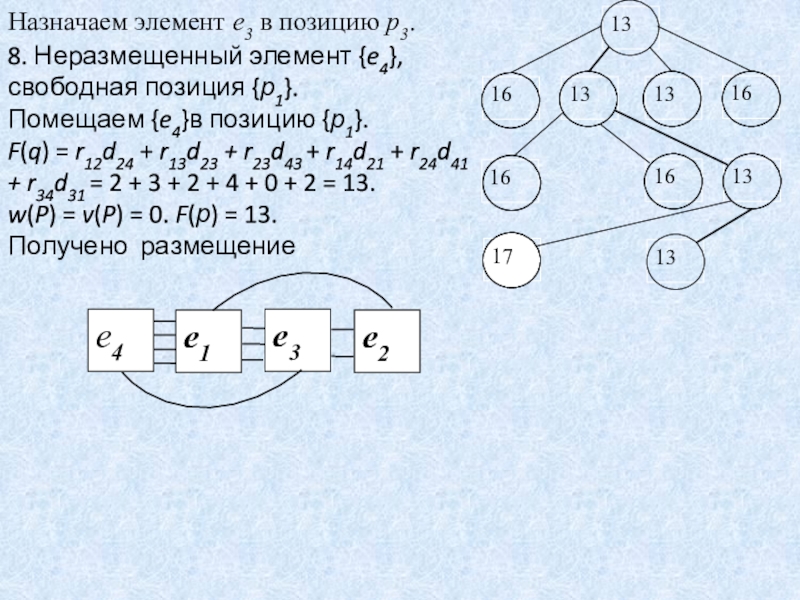
Слайд 66Назначаем элемент e3 в позицию р3.
8. Неразмещенный элемент {e4}, свободная
позиция {р1}.
Помещаем {e4}в позицию {р1}.
F(q) = r12d24 + r13d23 +
r23d43 + r14d21 + r24d41 + r34d31 = 2 + 3 + 2 + 4 + 0 + 2 = 13.
w(P) = v(P) = 0. F(р) = 13.
Получено размещение
Слайд 67Законы Мэрфи для программистов. Теория ошибок
Если отладка - процесс удаления
ошибок, то программирование должно быть процессом их внесения.
2. Ошибки
так же неисчерпаемы, как и атом.
Аксиома. В любой программе есть ошибки.
3. Закон пропорциональности. Чем более программа необходима, тем больше в ней ошибок.
Следствие. Ошибок не содержит лишь совершенно ненужная программа.
4. Фундаментальный закон теории ошибок. На ошибках учатся.
Следствие 1. Программист, написавший программу, становится ученым.
Следствие 2. Чем больше программист делает ошибок, тем быстрее он делается ученым.
Следствие 3. Крупный ученый-программист никогда не пишет правильные программы.
Замечание. На то он и ученый.
Слайд 685. Указание начинающему программисту. Если вы с первого раза сумели
написать программу, в которой транслятор не обнаружил ни одной ошибки,
сообщите об этом системному программисту. Он исправит ошибки в трансляторе.
7. Совет начинающему программисту. Никогда не исправляйте найденные ошибки, ибо это повлечет за собой появление неизвестного числа не найденных. Лучше опишите их в сопроводительной документации как особенность программы.
6. Программист может обнаружить ошибку только в чужой программе.
Следствие. Ошибке не все равно, кто ее обнаружит.
8. Ошибки могут следовать друг за другом.
9. От перестановки двух эквивалентных ошибок результат не меняется (коммутативность эквивалентных ошибок).
10. Две последовательные ошибки можно объединить в одну, более сильную.
11. . Одинаковые ошибки необязательно делать каждый раз, достаточно сделать одну, а затем обращаться к ней по мере необходимости из любого места программы.
Слайд 6913. Ошибки допускают многократное вложение друг в друга. Две одинаковые
вложенные ошибки называются четной ошибкой и ошибкой не являются.
12.
Ошибки могут вызывать друг друга и сами себя (рекурсивность ошибок).
14. Свойство четности ошибок. Если написанная программа сработала правильно, то это значит, что во время ее работы выполнилось четное число ошибок или программист не понял задание.
15. Во время исполнения ошибки имеют наивысший приоритет. Прервать исполнение ошибки может только другая, более активная ошибка.
16. Запросы операционной системы к ошибкам ошибками могут игнорироваться.
17. Запросы ошибок к операционной системе игнорироваться не могут.
18. На ЭВМ с параллельной архитектурой может выполняться несколько ошибок одновременно.
Слайд 7021. Программа-транслятор, предназначенная для перевода программ с языка высокого уровня
на машинный язык, при переводе порождает ошибки. Ошибки, которые содержались
в исходном описании, переводятся безошибочно.
19. Системные программы облегчают процесс написания прикладных программ и их ошибок.
20. Определение. Тестирование - это процесс нахождения ошибок в тесте. Хороший тест должен содержать ошибки, компенсирующие их нехватку в тестируемой программе.
23. Компьютер – устройство, разработанное для ускорения и автоматизации человеческих ошибок.
22. Независимое программное обеспечение не будет работать с ЛЮБЫМ программным обеспечением.
24. Не позволяйте компьютеру догадаться, что вы спешите.
25. Если что-то у Вас получилось кривовато, назовите это бета-версией.
26. Совет. До начала работы над проектом следует тщательно продумать все необходимые ошибки и связи между ними. Это значительно упростит работу над ошибками в самом проекте.