Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория массового обслуживания
Содержание
- 1. Теория массового обслуживания
- 2. Теория массового обслуживания начала развиваться в начале
- 3. Значительный вклад в создание и разработку общей
- 4. В зарубежной литературе теория массового обслуживания известна под названием «Теория очередей».
- 5. Для достижения этой цели ставятся задачи теории
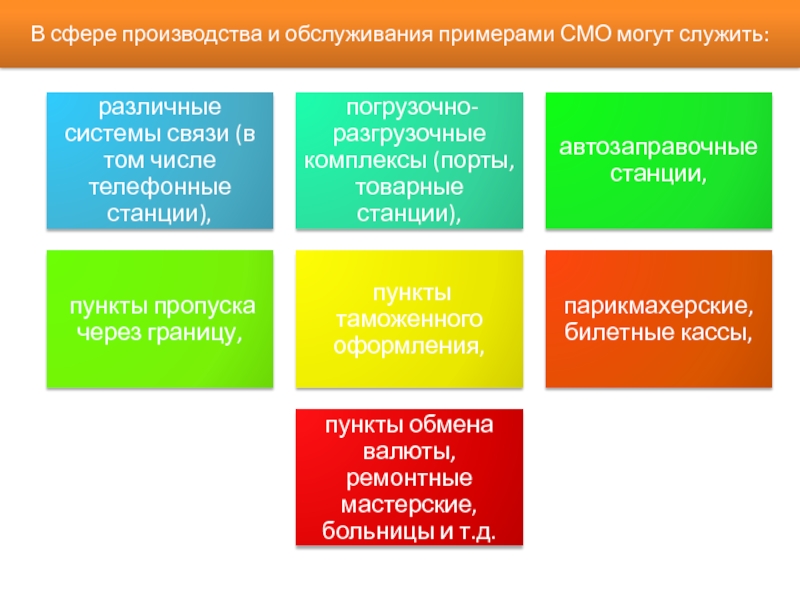
- 6. В сфере производства и обслуживания примерами СМО могут служить:
- 7. Такие системы как компьютерные сети, системы сбора,
- 8. Случайные процессы и потоки событийВ качестве аппарата
- 9. Потоком называется последовательность событий, наступающих одно за
- 10. Интенсивностью потока ʎ называют среднее число событий, которые появляются в единицу времени.
- 11. Теорема 8.1.Если постоянная интенсивность потока ʎ известна,
- 12. Пример 8.1.На автоматическую телефонную станцию поступает простейший
- 13. Каждая СМО включает в свою структуру некоторое
- 14. Обслуживание заявок, в общем случае, также длится
- 15. Таким образом, во всякой СМО можно выделить
- 16. В качестве характеристик эффективности функционирования СМО можно
- 17. По числу каналовОдноканальныеИмеется один канал обслуживанияМногоканальныеКоличество каналов
- 18. По дисциплине обслуживания СМО подразделяют на три класса
- 19. Ограничения ожидания могут касаться времени пребывания заявки
- 20. ОДНОКАНАЛЬНЫЕ СМО
- 21. Одноканальная СМО с отказами
- 22. Для составления матрицы перехода мы должны вычислитьИмеем:Перейдем
- 23. Слайд 23
- 24. Слайд 24
- 25. Слайд 25
- 26. Слайд 26
- 27. Слайд 27
- 28. Одноканальная СМО с ожиданием и ограниченной очередьюРассмотрим
- 29. Интенсивность потока обслуживаний автомобилей:Приведенная интенсивность потока автомобилей
- 30. Среднее число автомобилей, находящихся на обслуживании и
- 31. Одноканальная СМО с ожиданием и неограниченной очередьюПерейдем
- 32. Характеристики одноканальной СМО с ожиданием, без ограничения
- 33. Пример 9.3 Пусть рассматриваемое зона таможенного контроля
- 34. РешениеПараметр потока обслуживания и приведенная интенсивность потокаавтомобилей
- 35. Слайд 35
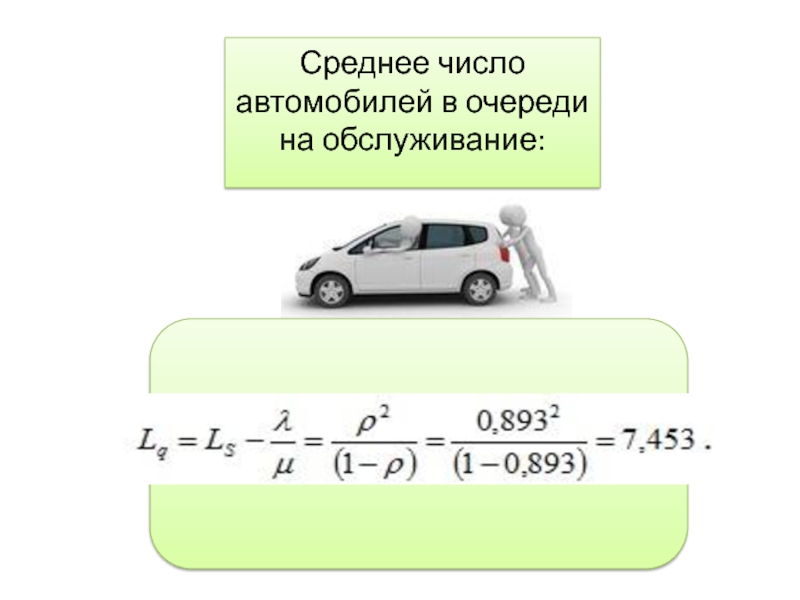
- 36. Среднее число автомобилей в очереди на обслуживание:
- 37. Слайд 37
- 38. Абсолютная пропускная способность:
- 39. Допустим, в первоначальном варианте количество мест для
- 40. Снятие ограничения на длину очереди позволяет увеличить
- 41. В подавляющем большинстве случаев на практике система
- 42. Стационарное решение системы имеет вид: гдеФормулы для
- 43. абсолютная пропускная способность среднее число каналов, занятых
- 44. Пример 9.4.Пусть n-канальная СМО представляет собой вычислительный
- 45. Предельные вероятности состояний найдем по формулам Эрланга:Вероятность
- 46. Таким образом, при установившемся режиме работы СМО
- 47. Многоканальная СМО с ожиданиемРассмотрим многоканальную систему массового
- 48. Остальные вероятностные характеристики функционирования в стационарном режиме
- 49. Требуется вычислить следующие предельные значения вероятностных характеристик
- 50. Вероятность отсутствия очереди на таможнеРотк≈Р0+Р1+Р2+Р3≈0,279+0,394+0,218+0,091=0,937.Среднее число заявок
- 51. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Теория массового обслуживания
это математическая теория, ставящая целью изучение систем
массового обслуживания (СМО).
Слайд 2Теория массового обслуживания начала развиваться в начале XX столетия.
Основоположником
теории массового обслуживания считается датский ученый Агнер Краруп Эрланг.
В
1909 г. Эрланг применил теорию вероятностей к исследованию зависимости обслуживания телефонных вызовов от числа поступивших на телефонную станцию вызовов. Слайд 3Значительный вклад в создание и разработку общей теории массового обслуживания
внес выдающийся советский математик Александр Яковлевич Хинчин (1984 – 1959).
Он предложил сам термин теория массового обслуживания и систематизировал основные положения теории системы массового обслуживания в монографии «Работы по математической теории массового обслуживания»
Слайд 4В зарубежной литературе теория массового обслуживания известна под названием «Теория
очередей».
Слайд 5Для достижения этой цели ставятся задачи теории массового обслуживания, состоящие
в установлении зависимостей эффективности функционирования СМО от ее организации (параметров):
Слайд 7Такие системы как компьютерные сети, системы сбора, хранения и обработки
информации, транспортные системы, автоматизированные производственные участки и, в военной области,
системы противовоздушной или противоракетной обороны также могут рассматриваться как своеобразные СМО.Слайд 8Случайные процессы и потоки событий
В качестве аппарата теории систем массового
обслуживания используют понятия теории случайных величин, а также теории случайных
процессов.Случайным процессом, или случайной функцией S(t), называется функция, которая каждому моменту времени t; из некоторого временного промежутка ставит в соответствие единственную случайную величину S(t).
Если состояния системы S изменяются во времени случайным образом, то будем говорить, что в системе S протекает случайный процесс.
По множеству состояний системы S протекающий в ней случайный процесс может быть дискретным или непрерывным.
Случайный процесс, протекающий в системе S , называется марковским, если обладает свойством отсутствия последействия, или отсутствия памяти, т.е. для любого фиксированного момента времени t0 вероятность состояния в будущем (при ) зависит только от состояния системы в настоящем (при ) и не зависит от того, как развивался этот процесс в прошлом (при ).
Слайд 9Потоком называется последовательность событий, наступающих одно за другим, в общем
случае, в случайные моменты времени.
События в потоке называются однородными,
если они различаются только по моментам времени их наступления, и неоднородными в противном случае.Поток событий называется потоком без последействия, или потоком без памяти, если для любой пары непересекающихся промежутков времени число событий за один из этих промежутков не зависят от числа событий за другой.
Очевидно, что регулярный поток событий, в котором события наступают через строго определенные промежутки времени, не обладает свойством отсутствия последействия, поскольку регулярность этого потока порождает последействие.
Слайд 10Интенсивностью потока ʎ называют среднее число событий, которые появляются в
единицу времени.
Слайд 11Теорема 8.1.
Если постоянная интенсивность потока ʎ известна, то вероятность появления
m событий простейшего потока за время длительностью определяется формулой Пуассона
Эта теорема является основополагающей для теории систем массового обслуживания.
Формула (8.1) отражает все свойства простейшего потока.
Формула не использует информации о появлении событий до начала рассматриваемого промежутка, что характеризует свойство отсутствия последействия. Легко можно убедиться, что формула отражает свойство ординарности.
Слайд 12Пример 8.1.
На автоматическую телефонную станцию поступает простейший поток вызовов с
интенсивностью λ =1,2 вызовов в минуту.
Найти вероятность того, что
за две минуты: а) не придет ни одного вызова;
б) придет ровно один вызов;
в) придет хотя бы один вызов.
Решение.
а) Случайная величина X – число вызовов за две минуты – распределена
по закону Пуассона с параметром λτ =1,2 ∙ 2 = 2,4 . Вероятность того, что вызовов не будет (m = 0 ), по формуле (8.1):
.
б) Вероятность одного вызова (m = 1) по формуле (8.1):
в) Вероятность хотя бы одного вызова:
.
.
.
Слайд 13Каждая СМО включает в свою структуру некоторое число обслуживающих устройств
(пунктов, приборов, линий), которые называют каналами обслуживания. Роль каналов могут
играть лица, выполняющие те или иные операции линии связи, автомашины, краны, ремонтные бригады, железнодорожные пути, бензоколонки.
Каждая СМО предназначена для обслуживания (выполнения) некоторого потока заявок (или требований), поступающих на вход системы большей частью не регулярно, а в случайные моменты времени.
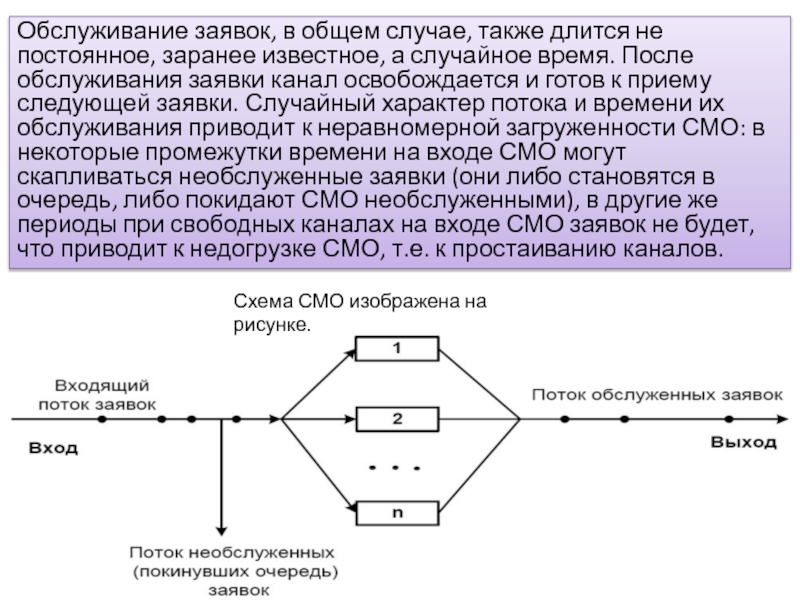
Слайд 14Обслуживание заявок, в общем случае, также длится не постоянное, заранее
известное, а случайное время. После обслуживания заявки канал освобождается и
готов к приему следующей заявки. Случайный характер потока и времени их обслуживания приводит к неравномерной загруженности СМО: в некоторые промежутки времени на входе СМО могут скапливаться необслуженные заявки (они либо становятся в очередь, либо покидают СМО необслуженными), в другие же периоды при свободных каналах на входе СМО заявок не будет, что приводит к недогрузке СМО, т.е. к простаиванию каналов.Схема СМО изображена на рисунке.
Слайд 15Таким образом, во всякой СМО можно выделить следующие основные элементы:
1)
входящий поток заявок;
2) очередь;
3) каналы обслуживания;
4) выходящий поток обслуженных заявок.
Каждая
СМО в зависимости от своих параметров: характера потока заявок, числа каналов обслуживания и их производительности, а также от правил организации работы, обладает определенной эффективностью функционирования (пропускной способностью), позволяющей ей более или менее успешно справляться с потоком заявок.Слайд 16В качестве характеристик эффективности функционирования СМО можно выбрать три основные
группы показателей:
Показатели эффективности использования СМО:
Абсолютная пропускная способность СМО – среднее
число заявок, которое сможет обслужить СМО в единицу времени.Относительная пропускная способность СМО – отношение среднего числа заявок, обслуживаемых СМО в единицу времени, к среднему числу поступивших за это же время заявок.
Средняя продолжительность периода занятости СМО.
Коэффициент использования СМО – средняя доля времени, в течение которого СМО занята обслуживанием заявок.
Показатели качества обслуживания заявок:
Среднее время ожидания заявки в очереди.
Среднее время пребывания заявки в СМО.
Вероятность отказа заявке в обслуживании без ожидания.
Вероятность того, что вновь поступившая заявка немедленно будет принята к обслуживанию.
Закон распределения времени ожидания заявки в очереди.
Закон распределения времени пребывания заявки в СМО.
Среднее число заявок, находящихся в очереди.
Среднее число заявок, находящихся в СМО.
Показатели эффективности функционирования пары «СМО – клиент», где под «клиентом» понимают всю совокупность заявок или некий их источник. К числу таких показателей относится, например, средний доход, приносимый СМО в единицу времени.
Слайд 17По числу каналов
Одноканальные
Имеется один канал обслуживания
Многоканальные
Количество каналов n ≥ 2
Практически
время обслуживания каналом одной заявки T об является непрерывной случайной
величиной. Однако при условии абсолютной однородности поступающих заявок и каналов время обслуживания может быть и величиной постоянной (T об = const).Классификация систем массового обслуживания
Слайд 19Ограничения ожидания могут касаться времени пребывания заявки в очереди, по
истечению которого она выходит из очереди и покидает систему, либо
касаться общего времени пребывания заявки в СМОСлайд 22Для составления матрицы перехода мы должны вычислить
Имеем:
Перейдем к решению следующей
важной задачи: нахождению вероятностей
и пребывания системы в каждом из возможных состояний.Слайд 28Одноканальная СМО с ожиданием и ограниченной очередью
Рассмотрим систему с ограниченной
очередью. Предположим, что независимо оттого, сколько требований поступает на вход
обслуживающей системы, данная система (очередь + обслуживаемые клиенты) не может вместить более N-требований (заявок), из которых одна обслуживается, а(N-1) ожидают, Клиенты, не попавшие в ожидание, вынуждены обслуживаться в другом месте и такие заявки теряются.
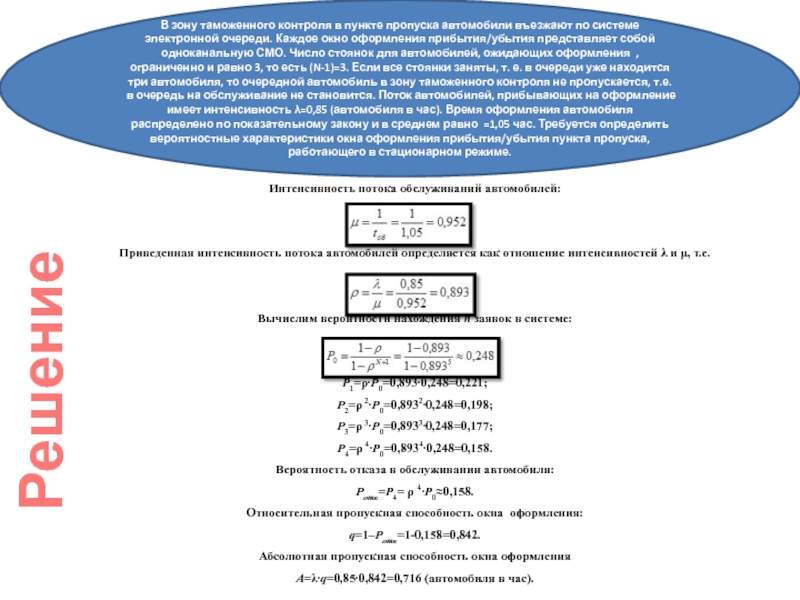
Слайд 29Интенсивность потока обслуживаний автомобилей:
Приведенная интенсивность потока автомобилей определяется как отношение
интенсивностей λ и μ, т.е.
Вычислим вероятности нахождения п заявок в
системе:P1=ρ∙P0=0,893∙0,248=0,221;
P2=ρ 2∙P0=0,8932∙0,248=0,198;
P3=ρ 3∙P0=0,8933∙0,248=0,177;
P4=ρ 4∙P0=0,8934∙0,248=0,158.
Вероятность отказа в обслуживании автомобиля:
Pотк=Р4= ρ 4∙P0≈0,158.
Относительная пропускная способность окна оформления:
q=1–Pотк=1-0,158=0,842.
Абсолютная пропускная способность окна оформления
А=λ∙q=0,85∙0,842=0,716 (автомобиля в час).
В зону таможенного контроля в пункте пропуска автомобили въезжают по системе электронной очереди. Каждое окно оформления прибытия/убытия представляет собой одноканальную СМО. Число стоянок для автомобилей, ожидающих оформления , ограниченно и равно 3, то есть (N-1)=3. Если все стоянки заняты, т. е. в очереди уже находится три автомобиля, то очередной автомобиль в зону таможенного контроля не пропускается, т.е. в очередь на обслуживание не становится. Поток автомобилей, прибывающих на оформление имеет интенсивность λ=0,85 (автомобиля в час). Время оформления автомобиля распределено по показательному закону и в среднем равно =1,05 час. Требуется определить вероятностные характеристики окна оформления прибытия/убытия пункта пропуска, работающего в стационарном режиме.
Решение
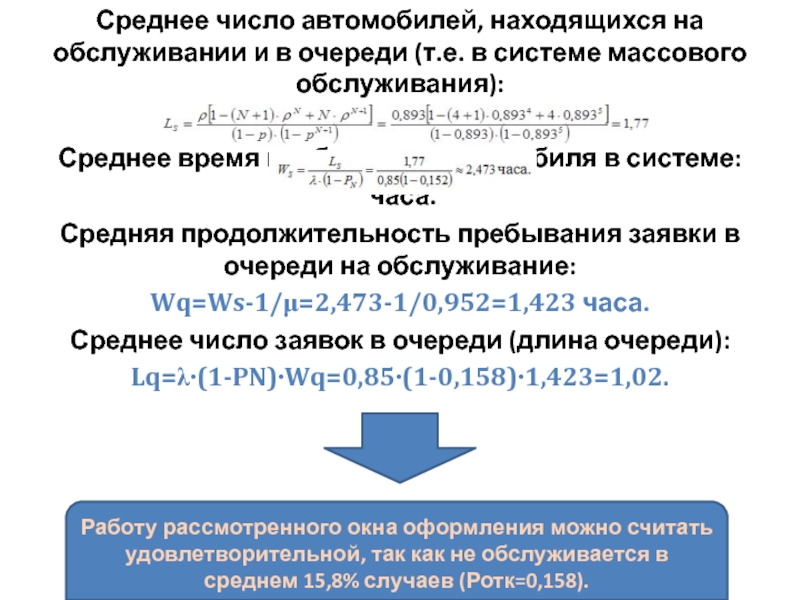
Слайд 30Среднее число автомобилей, находящихся на обслуживании и в очереди (т.е.
в системе массового обслуживания):
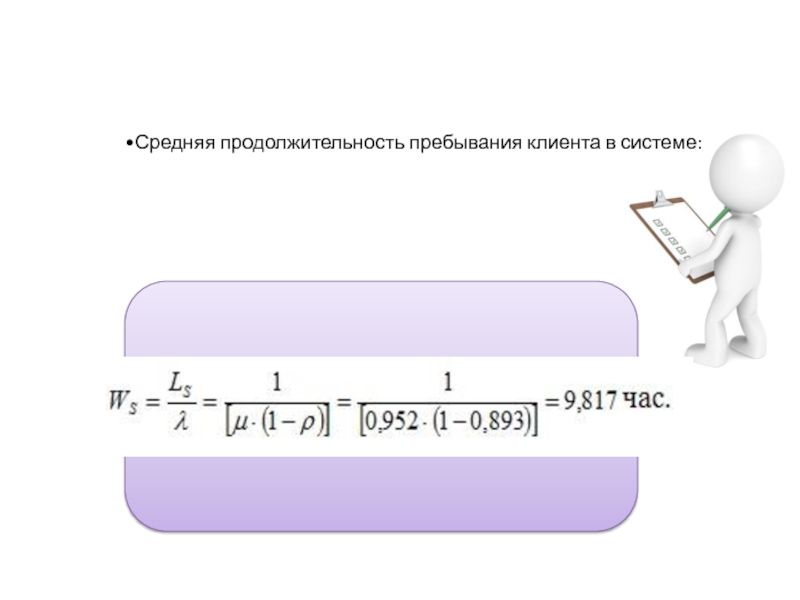
Среднее время пребывания автомобиля в системе:
часа.Средняя продолжительность пребывания заявки в очереди на обслуживание:
Wq=Ws-1/μ=2,473-1/0,952=1,423 часа.
Среднее число заявок в очереди (длина очереди):
Lq=λ∙(1-PN)∙Wq=0,85∙(1-0,158)∙1,423=1,02.
Работу рассмотренного окна оформления можно считать удовлетворительной, так как не обслуживается в среднем 15,8% случаев (Ротк=0,158).
Слайд 31Одноканальная СМО с ожиданием и неограниченной очередью
Перейдем теперь к рассмотрению
одноканальной СМО с ожиданием без ограничения на вместимость блока ожидания
(т.е. Ν → ∞). Остальные условия функционирования СМО остаются без изменений.Устойчивое решение в такой системе существует только тогда, когда λ<μ, то есть заявки должны обслуживаться с большей скоростью, чем поступают, в противном случае очередь может разрастись до бесконечности.
Вероятность того, что в системе находится п заявок, вычисляется по формуле
,n=0,1,2,…,
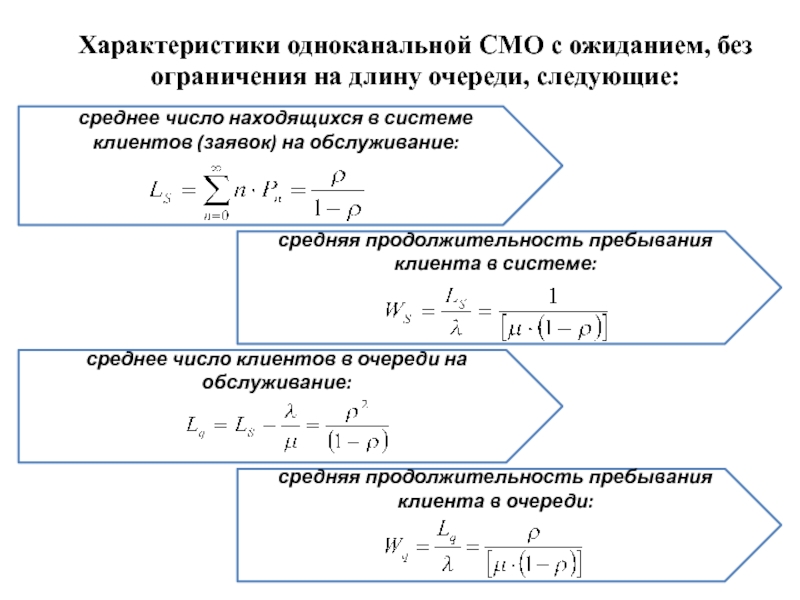
Слайд 32Характеристики одноканальной СМО с ожиданием, без ограничения на длину очереди,
следующие:
среднее число находящихся в системе клиентов (заявок) на обслуживание:
средняя продолжительность
пребывания клиента в системе:среднее число клиентов в очереди на обслуживание:
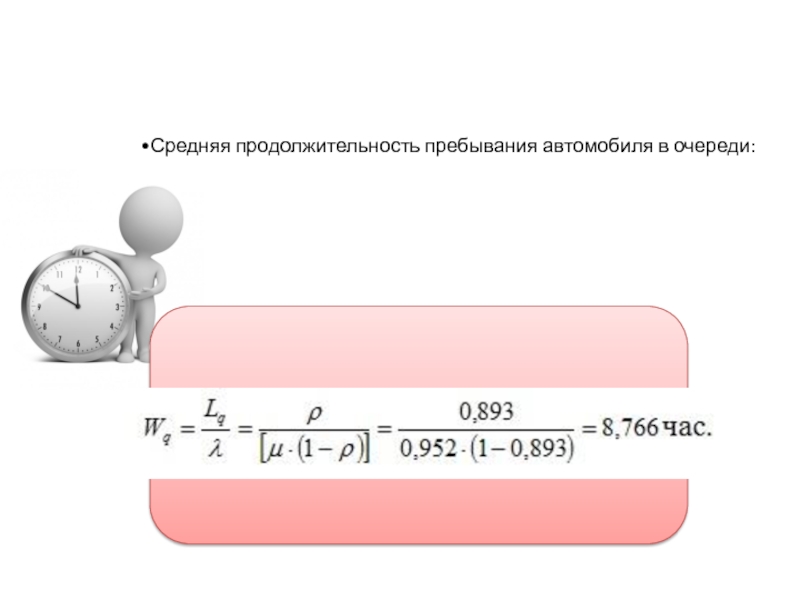
средняя продолжительность пребывания клиента в очереди:
Слайд 33Пример 9.3
Пусть рассматриваемое зона таможенного контроля в пункте пропуска
располагает неограниченным количеством площадок для стоянки прибывающих на оформление автомобилей,
т.е. длина очереди не ограничена. Требуется определить финальные значения следующих вероятностных характеристик:вероятности состояний системы (окна оформления);
среднее число автомобилей, находящихся в системе (на обслуживании и в очереди);
среднюю продолжительность пребывания автомобиля в системе (на обслуживании и в очереди);
среднее число автомобилей в очереди на обслуживании;
среднюю продолжительность пребывания автомобиля в очереди.
Слайд 34Решение
Параметр потока обслуживания и приведенная интенсивность потока
автомобилей ρ определены в
предыдущем примере: μ=0,952; ρ=0,893.
Вычислим предельные вероятности системы по формулам
P0=1- ρ
=1-0,893=0,107;P1=(1- ρ)· ρ =(1-0,893)·0,893=0,096;
P2=(1- ρ)· ρ 2=(1-0,893)·0,8932=0,085;
P3=(1- ρ)· ρ 3=(1-0,893)·0,8933=0,076;
P4=(1- ρ)· ρ 4=(1-0,893)·0,8934=0,068;
P5=(1- ρ)· ρ 5=(1-0,893)·0,8935=0,061 и т.д.
Следует отметить, что Р0 определяет долю времени, в течение которого окно оформления вынужденно бездействует (простаивает). В нашем примере она составляет 10, 7%, так как Р0=0,107. Среднее число автомобилей, находящихся в системе (на обслуживании и в очереди):
ед.
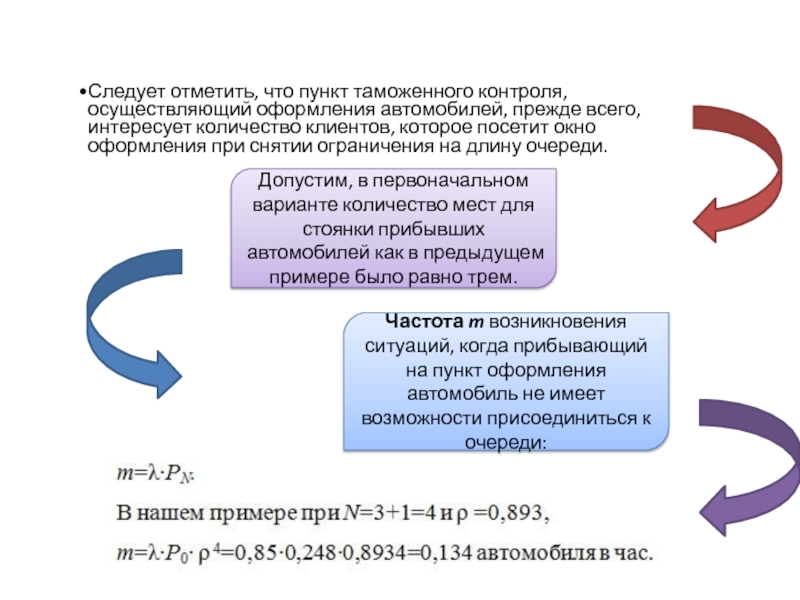
Слайд 39Допустим, в первоначальном варианте количество мест для стоянки прибывших автомобилей
как в предыдущем примере было равно трем.
Частота m возникновения
ситуаций, когда прибывающий на пункт оформления автомобиль не имеет возможности присоединиться к очереди:Слайд 40Снятие ограничения на длину очереди позволяет увеличить количество обслуживаемых клиентов
в нашем примере в среднем на 1,6 автомобиля за смену
(12 ч. работы) пункта оформления.Слайд 41В подавляющем большинстве случаев на практике система массового обслуживания является
многоканальными, то есть параллельно могут обслуживаться несколько заявок, и, следовательно,
модели с обслуживающими каналами (где число каналов обслуживания n>1) представляют несомненный интерес.Процесс массового обслуживания, описываемый данной моделью, характеризуется интенсивностью входного потока λ, при этом параллельно может обслуживаться не более n клиентов (заявок). Средняя продолжительность обслуживания одной заявки равняется . Режим функционирования того или иного обслуживающего канала не влияет на режим функционирования других обслуживающих каналов системы, при чем длительность процедуры обслуживания каждым из каналов является случайной величиной, починенной экспоненциальному закону распределения. Конечная цель использования параллельно включенных обслуживающих каналов заключается в повышение (по сравнению с одноканальной системой) скорости обслуживания требований за счет обслуживания одновременно n клиентов.
Многоканальная СМО с отказами
Слайд 42Стационарное решение системы имеет вид:
где
Формулы для вычисления вероятностей называются
формулами Эрланга.
Определим вероятностные характеристики функционирования многоканальной СМО с отказами в
стационарном режиме:вероятность отказа:
Так как заявка получает отказ, если приходит в момент, когда все каналы заняты. Величина Ротк характеризует полноту обслуживания входящего потока;
вероятность того, что заявка будет принята к обслуживанию (она же – относительная пропускная способность системы) дополняет Ротк до единицы:
Слайд 43абсолютная пропускная способность
среднее число каналов, занятых обслуживанием(
) следующее:
Величина характеризует степень загрузки СМО.
Слайд 44Пример 9.4.
Пусть n-канальная СМО представляет собой вычислительный центр (ВЦ) с
тремя (n=3) взаимозаменяемыми ПЭВМ для решения поступающих задач. Поток задач,
поступающих на ВЦ, имеет интенсивность λ=1 задача в час. Средняя продолжительность обслуживания tоб=1,8 час.Требуется вычислить значения:
- вероятности числа занятых каналов ВЦ;
- вероятности отказа в обслуживании заявки;
- относительной пропускной способности ВЦ;
- абсолютной пропускной способности ВЦ;
- среднего числа занятых ПЭВМ на ВЦ.
Определите, сколько дополнительно надо приобрести ПЭВМ, чтобы увеличить пропускную способность ВЦ в 2 раза.
Решение.
Определим параметр μ потока обслуживаний:
Приведенная интенсивность потока заявок
Слайд 45Предельные вероятности состояний найдем по формулам Эрланга:
Вероятность отказа в обслуживании
заявки
Относительная пропускная способность ВЦ
Абсолютная пропускная способность ВЦ:
Среднее число занятых каналов
– ПЭВМСлайд 46Таким образом, при установившемся режиме работы СМО в среднем будет
занято 1,5 компьютера из трех – остальные полтора будут простаивать.
Работу рассмотренного ВЦ вряд ли можно считать удовлетворительной, так как центр не обслуживает заявки в среднем в 18% случаев (Р3= 0,180). Очевидно, что пропускную способность ВЦ при данных λ и μ можно увеличить только за счет увеличения числа ПЭВМ.Определим, сколько нужно использовать ПЭВМ, чтобы сократить число не обслуженных заявок, поступающих на ВЦ, в 10 раз, т.е. чтобы вероятность отказа в решении задач не превосходила 0,0180. Для этого используем формулу вероятности отказа:
Составим следующую таблицу:
Анализируя данные таблицы, следует отметить, что расширение числа каналов ВЦ при данных значениях λ и μ до 6 единиц ПЭВМ позволит обеспечить удовлетворение заявок на решение задач на 99,22%, так как при n = 6 вероятность отказа в обслуживании (Ротк) составляет 0,0078.
Слайд 47Многоканальная СМО с ожиданием
Рассмотрим многоканальную систему массового обслуживания с ожиданием.
Процесс массового обслуживания при этом характеризуется следующим: входной и выходной
потоки имеют интенсивности λ и μ соответственно, параллельно обслуживаться могут не более С клиентов, то есть система имеет С каналов обслуживания.Средняя продолжительность обслуживания одного клиента равна
Вероятности того, что в системе находятся п заявок (С обслуживаются, остальные ожидают в очереди) равна:
где
Решение будет действительным, если выполняется следующее условие:
Слайд 48Остальные вероятностные характеристики функционирования в стационарном режиме многоканальной СМО с
ожиданием и неограниченной очередью определяется по следующим формулам:
среднее число клиентов
в очереди на обслуживаниесреднее число находящихся в системе клиентов (заявок на обслуживание и в очереди)
LS=Lq+ρ;
средняя продолжительность пребывания клиента (заявки на обслуживание) в очереди
средняя продолжительность пребывания клиента в системе
Рассмотрим примеры многоканальной системы массового обслуживания с ожиданием.
Пример 9.5. Таможня с тремя таможенными постами (каналами) выполняет пропуск товаров. Поток неправильно заполненных деклараций, для товаров прибывающих на таможню, - пуассоновский и имеет интенсивность λ=2,5 у.е. в сутки, среднее время оформления одной заявки распределено по показательному закону и равно tоб=0,5 часа. Предположим, что другой таможни в округе нет, и, значит, очередь деклараций может расти практически неограниченно.
Слайд 49Требуется вычислить следующие предельные значения вероятностных характеристик системы:
вероятность состояний системы;
среднее
число заявок в очереди на обслуживание;
среднее число находящихся в системе
заявок;среднюю продолжительность пребывания заявки в очереди;
среднюю продолжительность пребывания заявки в системе.
Решение.
Определим параметр потока обслуживаний
Приведенная интенсивность потока заявок
ρ=λ/μ=2,5/2,0=1,25,
при этом λ/μ ∙с=2,5/2∙3=0,41<1.
Поскольку λ/μ∙с<1, то очередь не растет безгранично и в системе наступает предельный стационарный режим работы.
Вычислим вероятности состояний системы:
Слайд 50Вероятность отсутствия очереди на таможне
Ротк≈Р0+Р1+Р2+Р3≈0,279+0,394+0,218+0,091=0,937.
Среднее число заявок в очереди на
обслуживание
Среднее число находящихся в системе заявок
Ls=Lq+ρ=0,111+1,25=1,361.
Средняя продолжительность пребывания заявки в
очереди на обслуживаниечаса
Средняя продолжительность пребывания заявки на таможне (в системе)
часа.