Слайд 1Теория вероятностей
Лекции по математике
Слайд 2И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Рекомендуемая литература
Кремер
Н.Ш. Теория вероятностей и математическая статистика. - М.: Банки и
биржи, ЮНИТИ, 2001 .
Гмурман В.Е. Теория вероятностей и математическая статистика. - М.: В.Ш., 2002 .
Тимошина И.Р. Электронный конспект лекций по теории вероятностей. ВФ СПбГУСЭ, 2007.
Слайд 3И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Содержание
Закон больших
чисел
Понятие о центральной предельной теореме Ляпунова
Функция одного случайного аргумента,
её распределение и числовые характеристики
Распределения: Хи квадрат, Стьюдента, Фишера-Снедекора
Слайд 4И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Закон
больших
чисел
Во многих случаях суммарное поведение достаточно большого числа случайных величин
утрачивает случайный характер и становится закономерным.
Для практики очень важно знание условий, при которых совокупное действие многих случайных причин приводит к результату, почти не зависящему от случая.
Слайд 5И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Закон больших
чисел
Знание этих условий позволяет предвидеть ход явлений.
Эти условия и
указываются в теоремах, носящих общее название закона больших чисел. Доказательство теорем основано на неравенстве Чебышева.
Слайд 6И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Неравенство Чебышева
Вероятность
того, что отклонение случайной величины X от её математического ожидания
по абсолютной величине меньше положительного числа ε, не меньше, чем :
Слайд 7И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Пример. Длина
изготовляемых изделий –
случайная величина. Её математическое
ожидание равно 90
см, дисперсия – 0,0225 см2.
Оценить вероятность того, что отклонение длины
изготовленного изделия от среднего значения
по абсолютной величине не превзойдёт 0,4 см.
Решение. Воспользуемся неравенством Чебышева:
Слайд 8И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
В нашем
примере:
Ответ. Примерно 86℅ деталей имеют длину,
отклоняющуюся от среднего значения
не более,
чем на 4 см.
Слайд 9И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Теорема Чебышева
Пусть
X1, X2 ,…, Xn - попарно независимые случайные величины, причём
их дисперсии не превосходят числа C. Тогда каким бы малым не было положительное число ε, выполняется условие:
Слайд 10И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Теорема Чебышева
Сущность
приведённой теоремы такова: среднее арифметическое большого числа случайных величин утрачивает
характер случайности.
Слайд 11И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Следствие
Если X1,
X2 ,…, Xn - попарно независимые случайные величины, имеющие одинаковые
математические ожидания, причём их дисперсии не превосходят числа С, то
M – математическое ожидание случайных
величин.
Слайд 12И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Теорема Бернулли
Если
в каждом из n независимых испытаний вероятность появления события равна
p, то каким бы малым не было положительное число ε, выполняется условие:
Слайд 13И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Теорема Бернулли
Здесь
m/n- относительная частота события A в серии n из испытаний.
Сущность
приведённой теоремы такова: при большом числе испытаний относительная частота утрачивает случайный характер и принимает значение, близкое к вероятности события.
Слайд 14И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Понятие о
центральной предельной теореме Ляпунова
В 1718 в Лондоне вышла в свет
книга французского математика А.Муавра (1667-1754) «Учение о случаях». Самое большое его достижение - открытие закономерности, которая очень часто наблюдается в случайных явлениях и получила название «нормального закона распределения».
Слайд 15И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Понятие о
центральной предельной теореме Ляпунова
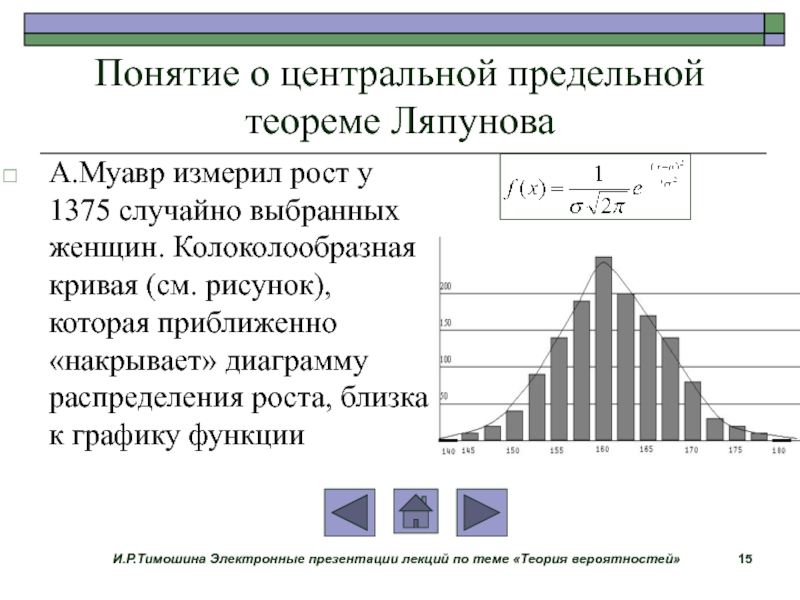
А.Муавр измерил рост у 1375 случайно выбранных
женщин. Колоколообразная кривая (см. рисунок), которая приближенно «накрывает» диаграмму распределения роста, близка к графику функции
Слайд 16И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Понятие о
центральной предельной теореме Ляпунова
Закон нормального распределения имеет важное практическое значение.
Так распределяется скорость газовых молекул, вес новорожденных и много других случайных событий физической и биологической природы. Для этих величин характерным является то, что на их формирование влияет большое число факторов, причем влияние каждого из них мало и ни один фактор не имеет значительного преимущества перед другими
Слайд 17И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Понятие о
центральной предельной теореме Ляпунова
Чем это объясняется? Ответ на этот вопрос
был дан выдающимся русским математиком А.М.Ляпуновым, сформулировавшем центральную предельную теорему.
Слайд 18И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Понятие о
центральной предельной теореме Ляпунова
Смысл этой теоремы заключается в следующем: если
случайная величина X представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на сумму ничтожно мало, то X имеет распределение, близкое к нормальному.
Слайд 19И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Функция одного
случайного аргумента и её распределение
Функцией одного случайного аргумента называют правило,
по которому каждому возможному значению случайной величины X соответствует одно возможное значение случайной величины Y: Y=φ(X).
Слайд 20И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Распределение значения
функции дискретного аргумента
Если различным возможным значениям аргумента X соответствуют различные
значения случайной величины Y, то вероятности соответствующих значений X и Y равны.
Слайд 21И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Пример 1.
Дискретная случайная величина X
задана распределением
Найти распределение случайной величины
Y= X2.
Слайд 22И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Решение. Найдём
возможные значения Y:
Слайд 23И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Распределение значения
функции дискретного аргумента
Если различным значениям X соответствуют значения Y, среди
которых есть равные, то следует складывать вероятности повторяющихся значений .
Слайд 24И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Пример 2.
Дискретная случайная величина X
задана распределением
Найти распределение случайной величины
Y= X2.
Слайд 25И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Решение. Найдём
возможные значения Y:
Слайд 26И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Распределение значения
функции непрерывного аргумента
Пусть Y=φ(X), где X - непрерывная случайная величина.
Доказано,
что если функция φ(X) является монотонно возрастающей или монотонно убывающей, то можно построить обратную функцию X=ψ(Y).
Слайд 27И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Распределение значения
функции непрерывного аргумента
В этом случае плотность распределения случайной величины Y
будет иметь вид:
Слайд 28И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Пример. Случайная
величина X равномерно
распределена на интервале [–1, 1]. Найти закон
распределения случайной величины Y=2X+3,
её математическое ожидание и дисперсию.
Решение. Плотность распределения случайной
величины X имеет вид:
Слайд 29И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Функция Y=2X+3
является монотонной, X=(Y-3)/2
обратная функция:
В соответствии с формулой
,
получим:
Слайд 30И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Математическое ожидание
M (Y)=3, дисперсия
Ответ.
M (Y)=3;
Слайд 31И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Математическое ожидание
функции случайного аргумента Y=φ(X)
Если Х – дискретная величина
Если Х
– непрерывная величина
Слайд 32И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Распределение значения
функции непрерывного аргумента
Можно доказать, что если непрерывная случайная величина X
распределена по нормальному закону, а случайная величина Y задаётся линейной функцией Y=AX+B, то величина Y также распределена по нормальному закону, причём
Слайд 33И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Пример. Найти
плотность распределения
случайной величины Y=3X+1, если величина X
распределена по
нормальному закону, M(X)= 2;
σ(X)=0,5.
Решение. Найдём математическое ожидание:
M(Y)=3M(X)+1=7.
Найдём среднее квадратическое отклонение:
σ(Y)=3· 0,5=1,5
Слайд 34И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Искомая плотность
распределения имеет вид:
Слайд 35И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Распределение «хи-квадрат»
Пусть
Xi (i=1,…,n)- нормально распределённые случайные величины, причём математическое ожидание каждой
из них равно нулю, а среднее квадратическое отклонение – единице. Тогда сумма квадратов этих величин также является случайной величиной:
Слайд 36И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Случайная
величина является функцией n случайных
аргументов:
X1, X2,…, Xn. Очевидно, что возможные значения этой величины неотрицательны. Закон распределения величины зависит от числа слагаемых, входящих в сумму и получил название «хи-квадрат» распределение.
Распределение «хи-квадрат»
Слайд 37И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Распределение «хи-квадрат»
Cлучайная
величина распределена
по закону «хи квадрат» с k=n степенями свободы. Плотность распределения этого закона имеет вид:
Слайд 38И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Распределение «хи-квадрат»
- гамма-функция, значения которой табулированы. Отсюда видно, что распределение «хи-квадрат» определяется одним параметром – числом степеней свободы k.
С увеличением числа степеней свободы распределение медленно приближается к нормальному.
Слайд 39И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Распределение Стьюдента
Пусть
Z - нормальная случайная величина, M(Z)=0; σ(Z) =1, а
- независимая от Z случайная величина, распределённая по закону «хи квадрат» с k степенями свободы.
Слайд 40И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Распределение Стьюдента
Тогда
величина
имеет распределение, которое называют t- распределением или распределением Стьюдента с
k степенями свободы.
С возрастанием числа степеней свободы распределение быстро стремится к нормальному.
Слайд 41И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Распределение Фишера-Снедекора
Пусть
и
- независимые случайные величины, имеющие «хи- квадрат» распределение соответственно с k1 и k2 степенями свободы. Тогда случайная величина
имеет распределение
Фишера – Снедекора.