Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория вероятностей
Содержание
- 1. Теория вероятностей
- 2. Теория вероятностей – это математическая наука, исследующая вероятностные закономерности массовых однородных случайных событий.
- 3. Каждое осуществление рассматриваемой совокупности условий называется опытом или испытанием. Результатом испытания является событие.
- 4. Случайными называют такие события, которые могут произойти или
- 5. Численная мера степени объективной возможности наступления случайного
- 6. Достоверному событию, т.е. событию, которое должно произойти при каждом испытании, приписывается вероятность Р(А)=1.
- 7. Невозможному событию, т.е. событию, которое не может произойти ни при одном испытании, приписывается вероятность Р(А)=0.
- 8. Вероятность случайного события заключена между нулем и единицей:
- 9. Несколько событий в данном опыте называются равновозможными,
- 10. Если из этих n единственно возможных, несовместных
- 11. Пример В ящике 10 перенумерованных шаров с номерами
- 12. Решение: Так как в ящике находятся 5 шаров
- 13. Формулы комбинаторики Комбинаторика – раздел математики, в
- 14. Перестановками называют комбинации, состоящие из одних и тех
- 15. Пример Сколько трехзначных чисел можно составить из цифр
- 16. Решение:Так как n=3, то искомое число трехзначных чисел P3 = 3! =123 = 6.
- 17. Размещениями называют комбинации, составленные из n различных элементов
- 18. Пример Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2?
- 19. Решение:Так как n=6, m=2, то искомое число
- 20. Сочетаниями называют комбинации, составленные из n различных элементов
- 21. Пример Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей?
- 22. Решение:Так как n=10, m=2, то искомое число способов равноодна комбинациявторая комбинация
- 23. Слайд 23
- 24. Пример В урне 10 шаров: 6 белых и
- 25. Решение: В этой задаче число всех случаев Число
- 26. Теоремы сложения и умножения вероятностей
- 27. Суммой (или объединением) нескольких случайных событий в данном
- 28. Теорема сложения вероятностей Если объединяемые события несовместны (никакие
- 29. Полная группа событий Если в результате данного испытания
- 30. Противоположное событие Событие, состоящее в не наступлении случайного
- 31. Молодой человек рассматривает три возможности уклониться от
- 32. Пусть событие А заключается в том, что
- 33. Так как Р(А)=0,5Р(В)=0,2Р(С)=0,01, тоР(А+В+С)=0,5+0,2+0,01=0,71
- 34. Произведением (или совмещением) двух случайных событий
- 35. Условная вероятность Под условной вероятностью события
- 36. Теорема умножения вероятностей (для двух событий) Вероятность совмещения
- 37. Независимые события Два случайных события
- 38. Для двух независимых событий вероятность их произведения равна произведению их вероятностей:
- 39. Студент сдает в сессию три экзамена. Вероятность
- 40. Пусть событие А1 состоит в том, что
- 41. Тогда по теореме умножения вероятностей Р(А)=Р(А1)Р(А2)Р(А3),где Р(А1)=0,4Р(А2)=0,5Р(А3)=0,7.Следовательно:Р(А)=0,4*0,5*0,7=0,14
- 42. Повторение испытаний Если производится n независимых испытаний в
- 43. Пример Определить вероятность того, что в семье,
- 44. Решение:Вероятность рождения девочки р=0,5, тогда Искомую вероятность находим по формуле: - вероятность рождения мальчика.
- 45. Формула полной вероятности Если известно, что событие
- 46. Студент, выйдя из дома за 30 минут
- 47. Н1- студент поехал автобусом; Н2- студент поехал троллейбусом; Н3-
- 48. Так как гипотезы образуют полную группу событий,
- 49. Слайд 49
- 50. Формула Байеса Условная вероятность события Нi в
- 51. Статистика запросов кредитов в банке: 10 %
- 52. Гипотезами в этой задаче будут: Н1- кредит взял
- 53. Условные вероятности события А для каждой из
- 54. Случайная величина называется дискретной, если множество ее
- 55. Случайная величина полностью определяется своим рядом распределения.
- 56. Пусть Х - дискретная случайная величина заданная
- 57. ДИСПЕРСИЯ И ЕЕ СВОЙСТВАДисперсия - это мера рассеяния значений случайной величины около ее математического ожидания:
- 58. Найдем математическое ожидание и дисперсию этой случайной величины. Например, пусть случайная величина Х задана рядом распределения:
- 59. Для вычисления дисперсии часто используют другую формулу:
- 60. Непрерывные случайные величины имеют бесконечное число возможных
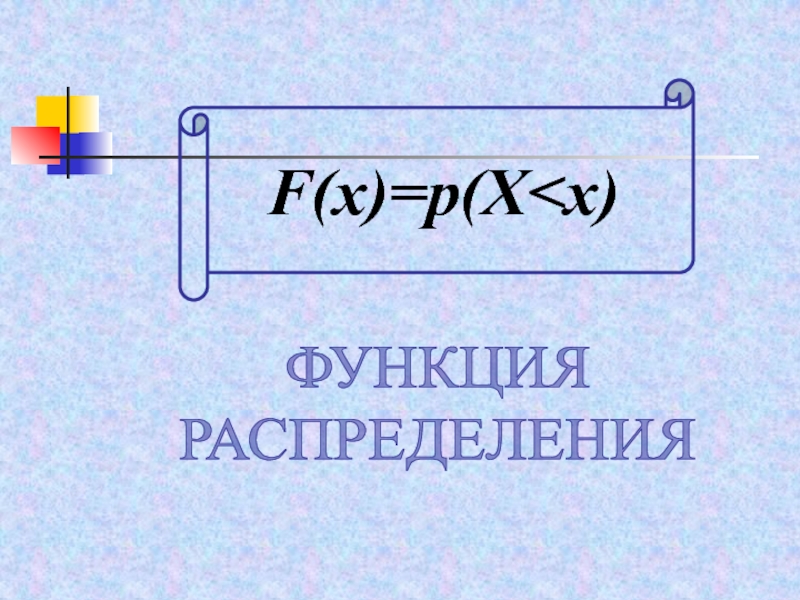
- 61. F(x)=p(X
- 62. ВЕРОЯТНОСТЬ ПОПАДАНИЯ СВНА ЗАДАННЫЙ ИНТЕРВАЛ
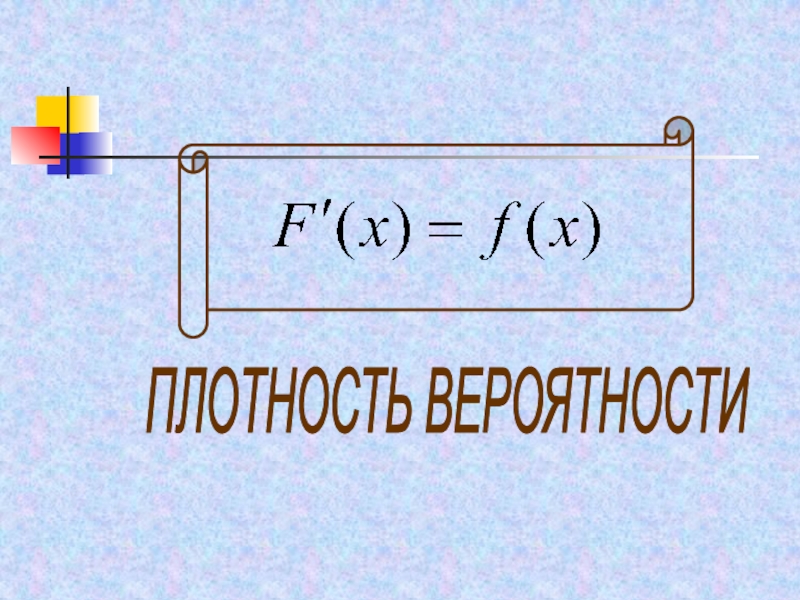
- 63. Функция f(x), равная производной от функции распределения, называется плотностью вероятности случайной величины Х или плотностью распределения.
- 64. ПЛОТНОСТЬ ВЕРОЯТНОСТИ
- 65. Выразим вероятность попадания на участок α до
- 66. Отсюда можно выразить функцию распределения через плотность вероятности:
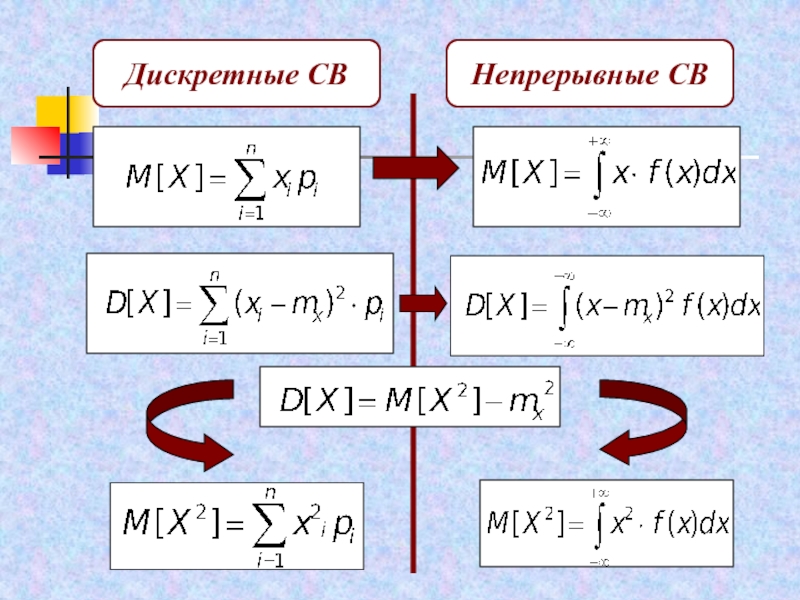
- 67. Дискретные СВНепрерывные СВ
- 68. Функция распределения непрерывной случайной величины задана
- 69. 1. Так как функция распределения F(x) непрерывна,
- 70. 3. Вычисление вероятности попадания на заданный участок
- 71. 2 способ. Используем формулу нахождения вероятности через плотность вероятности:4. Находим математическое ожидание:
- 72. 5. Находим дисперсию:Тогда
- 73. Случайная величина Х подчиняется закону распределенияНайти величину a и функцию распределения.ПРИМЕР.
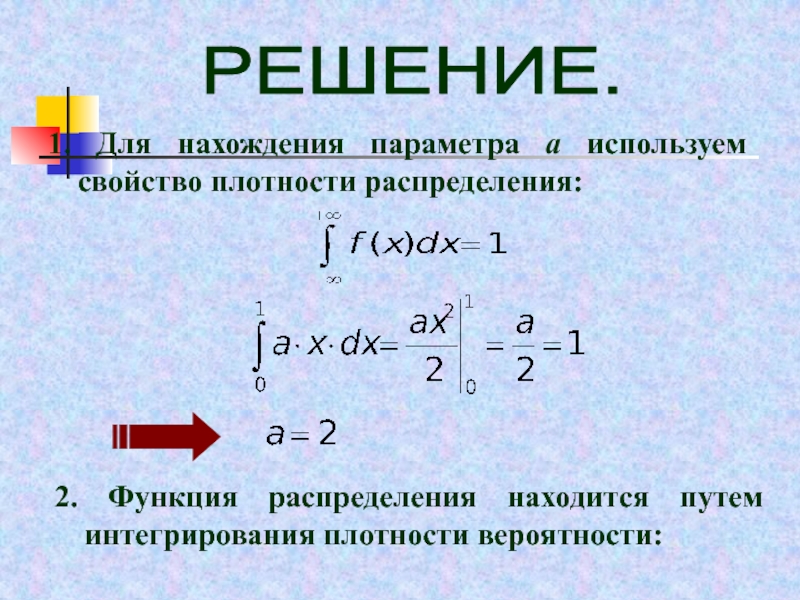
- 74. РЕШЕНИЕ.2. Функция распределения находится путем интегрирования плотности
- 75. При 0
- 76. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Теория вероятностей –
это математическая наука, исследующая вероятностные закономерности массовых
однородных случайных событий.
Слайд 3 Каждое осуществление рассматриваемой совокупности условий называется опытом или испытанием.
Результатом испытания
является событие.
Слайд 4Случайными
называют такие события, которые могут произойти или не произойти при
осуществлении совокупности условий, связанных с возможностью появления данных событий.
Случайные
события обозначают заглавными буквами латинского алфавита А, В, С... . Слайд 5 Численная мера степени объективной возможности наступления случайного события называется вероятностью.
Вероятность случайного события А обозначается через Р(А).
Слайд 6Достоверному событию,
т.е. событию, которое должно произойти при каждом испытании, приписывается
вероятность Р(А)=1.
Слайд 7Невозможному событию,
т.е. событию, которое не может произойти ни при одном
испытании, приписывается вероятность Р(А)=0.
Слайд 9 Несколько событий в данном опыте называются равновозможными, если появление какого-либо
из них не более возможно, чем любого другого.
Слайд 10 Если из этих n единственно возможных, несовместных и равновозможных случаев
m случаев связаны с наступлением события А (или, как говорят
в теории вероятностей, «благоприятствуют» А), то за вероятность события А принимается отношение m к n:Слайд 11Пример
В ящике 10 перенумерованных шаров с номерами 1, 2, …,
10. Вынули один шар. Какова вероятность того, что номер вынутого
шара четный?1
8
3
4
7
2
9
5
6
10
Слайд 12Решение:
Так как в ящике находятся 5 шаров с четными номерами,
то число элементарных событий, благоприятных событию А, равно 5, т.е.
и общее число исходов равно , то вероятность вынуть из ящика четный шар равна
2
4
6
8
10
Слайд 13Формулы комбинаторики
Комбинаторика – раздел математики, в котором изучаются вопросы
о том, сколько и каких различных комбинаций можно составить из
элементов некоторого множества.Слайд 14Перестановками
называют комбинации, состоящие из одних и тех же n различных
элементов и отличающиеся только порядком их расположения.
Число всех возможных
перестановок,
(факториал)
где n! = 123...n .
0! = 1.
Слайд 15Пример
Сколько трехзначных чисел можно составить из цифр 1, 2, 3,
если каждая цифра входит в изображение числа только один раз?
(123;
312;…)(221; 111;…)
Слайд 17Размещениями
называют комбинации, составленные из n различных элементов по m элементов,
которые отличаются либо составом элементов, либо их порядком.
Число всех
возможных размещений(m – множителей)
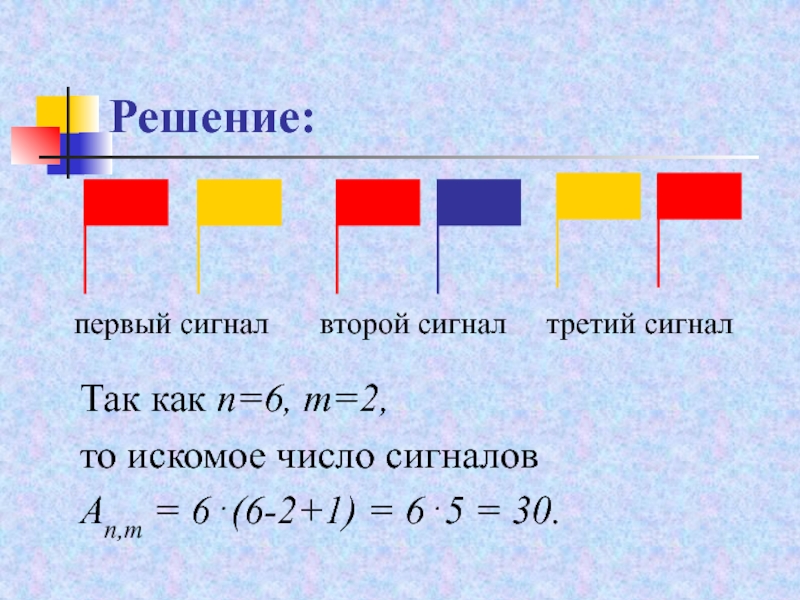
Слайд 19Решение:
Так как n=6, m=2,
то искомое число сигналов
An,m =
6(6-2+1) = 65 = 30.
первый сигнал
второй сигнал
третий
сигналСлайд 20Сочетаниями
называют комбинации, составленные из n различных элементов по m элементов,
которые отличаются хотя бы одним элементом.
Число сочетаний
Слайд 24Пример
В урне 10 шаров: 6 белых и 4 черных. Вынули
два шара.
Какова вероятность,
что оба шара – белые?
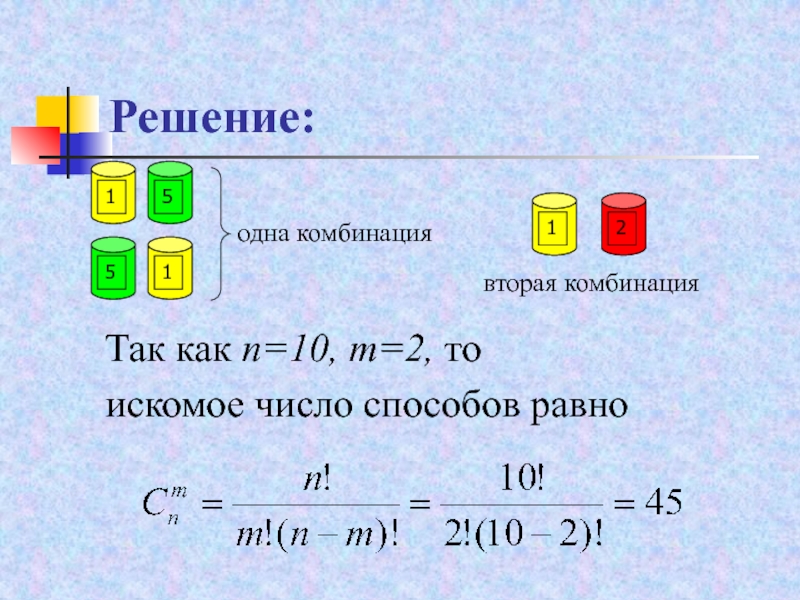
Слайд 25Решение:
В этой задаче число всех случаев
Число же случаев, благоприятных
событию А, определяется равенством , т.е. . Итак,
Слайд 27Суммой (или объединением)
нескольких случайных событий
в данном опыте называется новое
событие, состоящее в осуществлении одного из данных событий, и обозначается
символом .Слайд 28Теорема сложения вероятностей
Если объединяемые события несовместны (никакие два из них
не могут осуществляться одновременно), то вероятность суммы нескольких событий равна
сумме вероятностей объединяемых событий :Слайд 29Полная группа событий
Если в результате данного испытания может наступить лишь
одно из несовместных событий
, образующих так называемую полную группу событий.Так как объединение событий полной группы является событием достоверным, то для таких событий имеет место равенство
Слайд 30Противоположное событие
Событие, состоящее в не наступлении случайного события А, называется
событием, противоположным событию А, и обозначается через .
Объединение событий А и дает событие достоверное, а поскольку события А и несовместны, то
или
Слайд 31Молодой человек рассматривает три
возможности уклониться от службы в армии.
Во-первых, он может поступить учиться в ВУЗ,
во-вторых, он может
быть освобожден от армии по состоянию здоровья, и в третьих,
он может жениться и к моменту призыва
обзавестись двумя детьми. Вероятности этих
событий для него равны, соответственно, 0,5;
0,2 и 0,01. Считая эти события несовместными,
найти вероятность того, что молодой
человек не попадет в ряды призывников.
Пример
Слайд 32Пусть событие А заключается в том, что молодой человек поступит
в ВУЗ,
событие В - что он получит освобождение по
состоянию здоровья событие С - что он женится и обзаведется двумя детьми.
Т.к. эти события несовместны, то применяем теорему о сложении вероятностей в виде:
Р(А+В+С)=Р(А)+Р(В)+Р(С)
Решение:
Слайд 34Произведением
(или совмещением)
двух случайных событий и
в данном опыте называется новое событие
, заключающееся в совместном появлении обоих событий.Слайд 35Условная вероятность
Под условной вероятностью события по отношению
к событию (обозначается ) понимается вероятность события
, определенная в предположении, что событие произошло.Слайд 36Теорема умножения вероятностей (для двух событий)
Вероятность совмещения двух событий
и равна произведению вероятности одного из них на условную
вероятность второго по отношению к первому:Слайд 37Независимые события
Два случайных события и называются независимыми,
если условная вероятность одного из них по отношению к другому
равна безусловной вероятности этого же события:Слайд 38 Для двух независимых событий вероятность их произведения равна произведению их
вероятностей:
Слайд 39Студент сдает в сессию три экзамена.
Вероятность воспользоваться шпаргалкой
на
первом, втором и третьем экзамене равна
соответственно 0,4; 0,5; 0,7.
Найти вероятность того, что на всех
экзаменах студенту удастся списать.
Пример
Слайд 40Пусть событие А1 состоит в том, что студенту удалось списать
на первом экзамене,
А2 - на втором экзамене,
А3 - на третьем
экзамене.Эти события будут независимыми. Событие А, состоящее в том, что студент спишет на всех трех экзаменах, выразится как произведение событий А1, А2 и А3 :
А=А1А2А3
Решение:
Слайд 41Тогда по теореме умножения вероятностей
Р(А)=Р(А1)Р(А2)Р(А3),
где Р(А1)=0,4
Р(А2)=0,5
Р(А3)=0,7.
Следовательно:
Р(А)=0,4*0,5*0,7=0,14
Слайд 42Повторение испытаний
Если производится n независимых испытаний в одинаковых условиях, в
каждом из которых вероятность появления события A одно и та
же и равна р, то вероятность того, что событие А появится в этих n испытаниях m раз, выражается формулой:,где
формула Бернулли
Слайд 43 Пример
Определить вероятность того, что в семье, имеющей пять детей,
будет три девочки и два мальчика. Вероятности рождения мальчика и
девочки считаются одинаковыми.Слайд 44Решение:
Вероятность рождения девочки р=0,5, тогда
Искомую вероятность находим по формуле:
- вероятность рождения
мальчика.
Слайд 45Формула полной вероятности
Если известно, что событие А может произойти
вместе с одной из гипотез Н1, Н2, … , Нn
, образующими полную группу событий,
то событие А можно представить как объединение
событий АН1, АН2, … , АНn,
т.е. А= АН1 + АН2 + … + АНn.
Вероятность события А можно определять по
формуле полной вероятности
или
Слайд 46Студент, выйдя из дома за 30 минут до начала
занятий,
может приехать в институт автобусом,
троллейбусом или трамваем. Все эти
варианты равновозможные. Вероятность приехать на занятия
вовремя для этих видов транспорта соответственно
равна 0,99; 0,98 и 0,9. Какова вероятность,
что студент приедет на учебу вовремя?
Пример
Слайд 47 Н1- студент поехал автобусом;
Н2- студент поехал троллейбусом;
Н3- студент поехал трамваем.
Чтобы
использовать формулу полной вероятности, необходимо знать вероятности каждой из гипотез
и условные вероятности события А для каждой из гипотез. Пусть событие А заключается в том, что студент не опоздает на занятия. Оно может произойти только вместе с одной из гипотез:
Решение:
Слайд 48Так как гипотезы образуют полную группу событий, то суммарная вероятность
всех гипотез равна 1.
По условию задачи все гипотезы
равновероятны, следовательно Р(Н1)=Р(Н2)=Р(Н3)=1/3.
Условные вероятности события А для каждой из гипотез даны по условию задачи:
Р(А|Н1)=0,99; Р(А|Н2)=0,98; Р(А|Н3)=0,9
Следовательно, по формуле полной вероятности,
Слайд 50Формула Байеса
Условная вероятность события Нi
в предположении, что событие
А имеет место,
определяется по формуле Байеса:
Слайд 51Статистика запросов кредитов в банке:
10 % - государственные органы,
30 % - банки, 60 % - физические лица.
Вероятности невозврата
кредита для них соответственно равны 0,01; 0,05; 0,2.
Найти вероятность события А - невозврата
очередного кредита и вероятность события В –
что кредит не возвратил некоторый банк, если
известно, что событие А произошло.
Пример
Слайд 52 Гипотезами в этой задаче будут:
Н1- кредит взял государственный орган;
Н2- кредит
взял банк;
Н3- кредит взяло физическое лицо.
Вероятность события А найдем по
формуле полной вероятности. Найдем вероятности гипотез:
Р(Н1)=0,1; Р(Н2)=0,3; Р(Н3)=0,6
Решение:
Слайд 53Условные вероятности события А для каждой из гипотез даны в
задаче:
Р(А|Н1)=0,01; Р(А|Н2)=0,05; Р(А|Н3)=0,2.
Тогда:
Вероятность события В - это условная вероятность
гипотезы Н2 : Р(Н2/А). Находим ее по формуле Байеса:Слайд 54Случайная величина называется дискретной,
если множество ее возможных значений
cчетно
(т.е. все возможные значения
можно пронумеровать натуральными
числами)
{x1,x2,…xn}
Случайной величиной
называется величина, которая в результате опыта
принимает заранее неизвестное численное
значение.
Слайд 55Случайная величина полностью определяется своим рядом распределения.
Ряд распределения представляет
собой
таблицу, в которой указаны
возможные значения случайной
величины и
их вероятности: Слайд 56Пусть Х - дискретная случайная величина заданная рядом распределения:
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ
И
ЕГО СВОЙСТВА
Математическим ожиданием M[X] случайной
величины Х называется сумма
рядаСлайд 57ДИСПЕРСИЯ И ЕЕ СВОЙСТВА
Дисперсия - это мера рассеяния
значений случайной
величины
около ее математического
ожидания:
Слайд 58Найдем математическое ожидание и дисперсию этой случайной величины.
Например, пусть
случайная величина Х задана рядом распределения:
Слайд 60Непрерывные случайные величины имеют бесконечное число возможных значений. Поэтому ввести
для них ряд распределения нельзя.
НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ
ВЕЛИЧИНЫ
Слайд 63Функция f(x), равная производной
от функции распределения, называется
плотностью вероятности
случайной
величины Х или плотностью
распределения.
Слайд 65Выразим вероятность попадания на участок α до β через f(x).
Она равна сумме элементов вероятности на этом участке, т.е. интегралу:
Слайд 68 Функция распределения непрерывной
случайной величины задана выражением:
Найти величину a,
плотность вероятности,
вероятность попадания на участок (0.25-0.5),
математическое ожидание и
дисперсию .ПРИМЕР.
Слайд 691. Так как функция распределения F(x) непрерывна, то при х=1
ax2=1, следовательно, a=1.
2. Плотность вероятности находится, как производная от функции
распределения:РЕШЕНИЕ.
Слайд 703. Вычисление вероятности попадания на заданный участок может быть произведено
двумя способами: с помощью функции распределения и с помощью плотности
вероятности.1 способ.
Используем формулу нахождения вероятности через функцию распределения:













































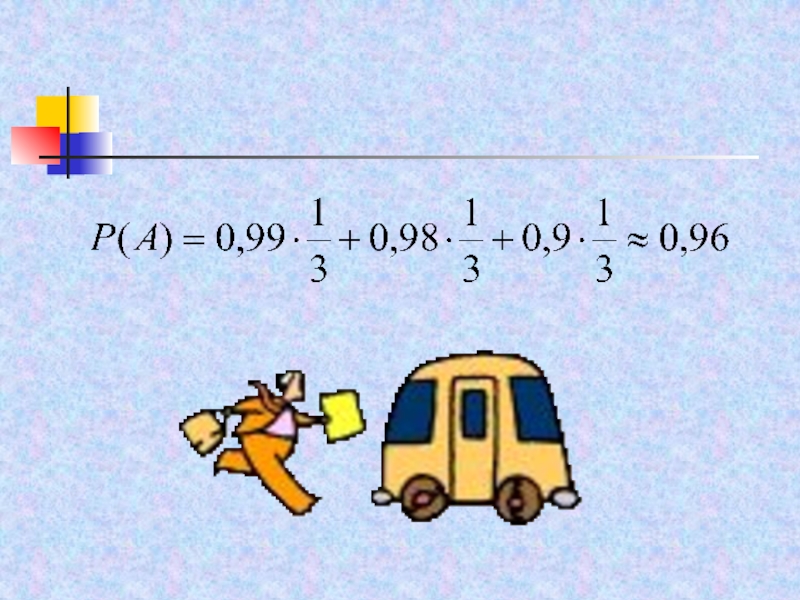






![Теория вероятностей Пусть Х - дискретная случайная величина заданная рядом распределения:МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ И Пусть Х - дискретная случайная величина заданная рядом распределения:МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ И ЕГО СВОЙСТВАМатематическим ожиданием M[X] случайной величины](/img/thumbs/9744195ee4381aa730739c602a937254-800x.jpg)