Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория вероятностей и математическая статистика
Содержание
- 1. Теория вероятностей и математическая статистика
- 2. Лекция 11 Гистограмма распределенияКритерий согласия хи-квадратТема 8. Оценка закона распределнияОценка закона распределения
- 3. ЛитератураC.35-41 [1]C.134-143 [2]
- 4. Эмпирическая функция распределенияТема 8. Оценка закона распределенияЭмпирической
- 5. Гистограмма распределения . Эмпирической
- 6. Полигон частот .
- 7. Гистограмма. Полигон частот. Выбор количества интервалов
- 8. Выборочные характеристики .
- 9. Выборочные характеристики .
- 10. Критерий согласия Хи-квадрат (критерий Пирсона)Тема 8. Оценка
- 11. Критерий согласия Хи-квадрат (критерий Пирсона)(Тема 8. Оценка
- 12. Применение правила критерия сводится к следующему:На основании
- 13. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Лекция 11
Гистограмма распределения
Критерий согласия хи-квадрат
Тема 8. Оценка закона распределния
Оценка закона
распределения
Слайд 3Литература
C.35-41 [1]
C.134-143 [2]
Горяинов, В.Б.,
и др., Математическая статистика, под ред. В.С. Зарубин and А.П.
Крищенко. 2001, М.: Издательство МГТУ им. Н.Э. Баумана. 424.Фигурин, В.А. and В.В. Оболонкин, Теория вероятностей и математическая статистика. 2000, Минск: ООО "Новое знание". 207.
Тема 8. Оценка закона распределения
Слайд 4Эмпирическая функция распределения
Тема 8. Оценка закона распределения
Эмпирической функцией распределения (функцией
распределения выборки) называют функцияю F*(x)=ni/n , ni – число элементов
выборки меньших x, n – объем выборки.Свойства функции распределения.
Значения функции распределения принадлежат отрезку [0;1]
Функция распредлеения F*(x) – неубывающая функция.
Если x1 – наименьшее значение выборки, а xk – наибольшее, то
F*( x)=0 при x
Функция распределения определяет для каждого x относительную частоту события
X
Слайд 5Гистограмма распределения
.
Эмпирической плотностью распределения соответствующей
реализаци случайной выборки
из генеральной совокупности X, называют функцию, которая во всех точках интервала Ji, i=1,m равна ni/(nΔ), а вне интервала J равна 0. Δ – длина интервалов Ji.
Для больших объемов выборки, удобно строить статистический ряд. В нижней строке таблицы – отностительные частоты появления . Разделив это значение на длину интервала – получим значения плотности распределения в данном интервале Δ.
Функция pn(x) – кусочно постоянная. График этой функции называется гистограммой.
Тема 8. Оценка закона распределения
Слайд 6Полигон частот
.
Часто гистограммой называют диаграмму, составленную из прямоугольников с основанием
Δ и высотами ni/(nΔ), i=1,m. Суммарная площадь всех прямогуольников равна 1. Площадь каждого прямоугольника ni/n – частота попадания элементов выборки в соотвествующий интервал.
Наряду с гистограммой часто используют другое графическое представление функции p(x) – полигон частот.
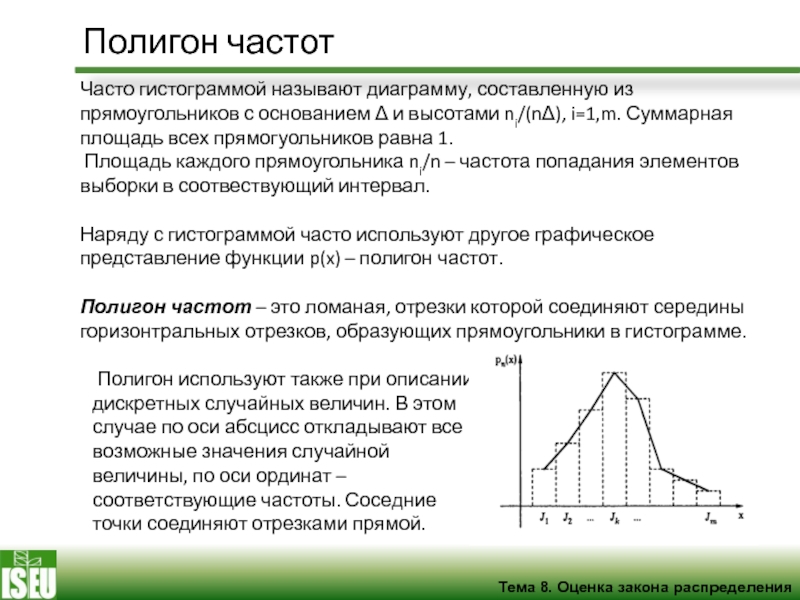
Полигон частот – это ломаная, отрезки которой соединяют середины горизонтральных отрезков, образующих прямоугольники в гистограмме.
Полигон используют также при описании дискретных случайных величин. В этом случае по оси абсцисс откладывают все возможные значения случайной величины, по оси ординат – соответствующие частоты. Соседние точки соединяют отрезками прямой.
Тема 8. Оценка закона распределения
Слайд 7Гистограмма. Полигон частот. Выбор количества интервалов
.
Выбор количества интервалов.
Выбор количества интервалов существенно
зависит от объема данных. В литературе приводятся несколько руководств по выбору числа интервалов.Например,
Формула Старджеса:
m=log2n+1=3,32ln n +1.
Другие методы расчета
m=5 ln n
m=n^(1/2)
Формулы следует рассматривать как оценку снизу для количества интервалов.
Тема 8. Оценка закона распределения
Слайд 8Выборочные характеристики
.
Аналогично рассматриваются числовые характеристики генеральной совокупности (теоретические числовые характеристики )
и выборочные числовые характеристики.По определению выборочный начальный момент k- того порядка
Выборочный начальный момент первого порядка – выборочное среднее.
Выборочный центральный момент k-того порядка
Выборочный центральный момент 2-го порядка - выборочная дисперсия.
Выборочное среднее квадратичное отклонение
Тема 8. Оценка закона распределения
Слайд 9Выборочные характеристики
.
Выборочные характеристики можно ввести также и при рассмотрении выборок из
многомерных генеральных совокупностей. Основное свойство выборочных моментов, как начальных, так и центральных, и в том числе выборочного среднего и выборочной дисперсии, состоит в том, что при увеличении объема выборки n они сходятся по вероятности к соответствующим теоретическим (генеральным) моментам*.
Тема 8. Оценка закона распределения
Слайд 10Критерий согласия Хи-квадрат (критерий Пирсона)
Тема 8. Оценка закона распределения
Сравнение теоретического
и эмпирического распределений производится с помощью правила – критерия согласия.
Критерий
Пирсона, или критерий χ² (Хи-квадрат) — наиболее часто употребляемый критерий для проверки гипотезы о законе распределения. Обозначим через X исследуемую случайную величину. Пусть требуется проверить гипотезу о том, что эта случайная величина подчиняется закону распределения F(x). Для проверки гипотезы произведём выборку, состоящую из n независимых наблюдений над случайной величиной X. По выборке можно построить эмпирическое распределение F * (x) исследуемой случайной величины.
Для проверки критерия вводим статистику. (статистика – функция случайной выборки)
- предполагаемая вероятность попадания в i-тый интервал.
– соответствующее эмпирическое значение, ni- число элементов выборки из i-того интервала, N – полный объем выборки.
X – случайная величина , следовательно хи-квадрат тоже случайная величина и должна подчиняться распределению «хи-квадрат».
Слайд 11Критерий согласия Хи-квадрат (критерий Пирсона)
(
Тема 8. Оценка закона распределения
Правило критерия
Если
полученная статистика превосходит квантиль закона распределения χ2 заданного уровня значимости
α с l=(k-p-1) степенями свободы, где k – число наблюдений, p – число оцениваемых параметров закона распределения, то гипотеза отвергается. В противном случае гипотеза принимается на заданном уровне значимости.Кванти́ль в математической статистике — такое число, что заданная случайная величина не превышает его лишь с фиксированной вероятностью. Квантиль xp порядка p F(xp)=p.
Слайд 12Применение правила критерия сводится к следующему:
На основании выборочных данных x1,
x2, …xn находят оценки параметров теоретического распределения.
Вычисляют по теоретическому распределению
вероятности попадания случайной величины в i-тые интервалы ( ).Рассчитывают значение статистики χ2 .
Определяют число степеней свободы.
Выбирают уровень значимости α – как правило 0,05 или 0,01.
По таблицам находят квантиль распределния «хи-квадрат» χ2l,α .
Если статистика χ2 больше χ2α, то гипотеза отвергается при уровне значимости α .
Критерий согласия Хи-квадрат (критерий Пирсона)
(
Тема 8. Оценка закона распределения


![Теория вероятностей и математическая статистика ЛитератураC.35-41 [1]C.134-143 [2] Горяинов, В.Б., и др., Математическая ЛитератураC.35-41 [1]C.134-143 [2] Горяинов, В.Б., и др., Математическая статистика, под ред. В.С.](/img/thumbs/9da51216ca451cc5bbe3ca890075b728-800x.jpg)