Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ТЕОРІЯ АЛГОРИТМІВ
Содержание
- 1. ТЕОРІЯ АЛГОРИТМІВ
- 2. Мета курсу допомогти майбутнім програмістам навчитися: Поставити
- 3. Основна літератураАхо А., Хопкрофт Д., Ульман Д.
- 4. Додаткова літератураКнут Д. Искусство программирования, т.3. Сортировка
- 5. Структура курсуПобудова і аналіз алгоритмівМетоди розробки алгоритмівОсновні
- 6. Оцінювання роботиПрактичні роботи (по 10 балів): Побудова
- 7. АтестаціяІ атестація 25
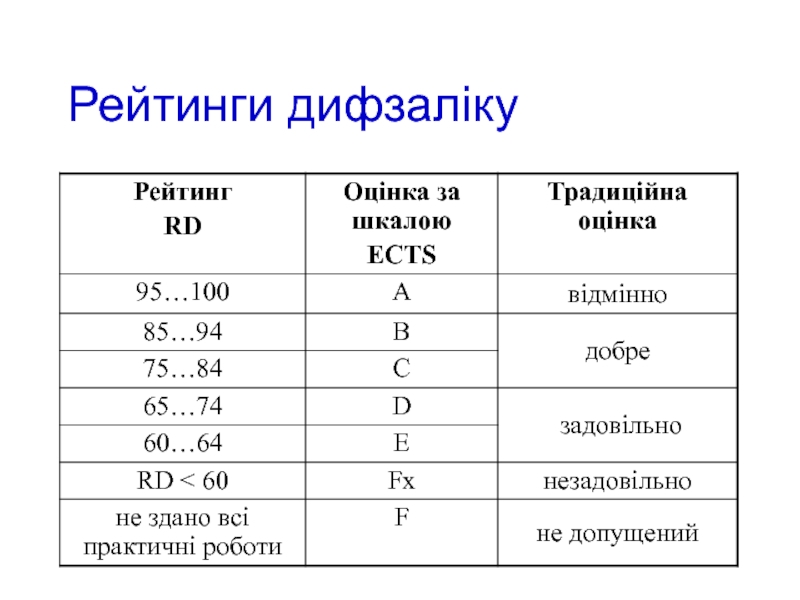
- 8. Рейтинги дифзаліку
- 9. Розділ 1. Побудова і аналіз алгоритмів
- 10. 1.1. Від задачі до програми Література для
- 11. Постановка задачі Щоб зрозуміти задачу, потрібно точно її
- 12. Приклад Андрій – агент по продажу кондиціонерів
- 13. Що дано? Вхідна інформація задана у вигляді
- 14. Що ми хочемо знайти? Ми хочемо допомогти
- 15. Тому ми повертаємося до Андрія і вимагаємо
- 16. Побудова моделі Вибір моделі суттєво впливає на решту
- 17. На вибір відповідної математичної структури будуть впливати
- 18. Зробивши пробний вибір математичної структури, задачу слід
- 19. Приклад. Повернемося до задачі Андрія. Чи розв’язували
- 20. Слайд 20
- 21. Що ми шукаємо в задачі? В термінах
- 22. Розробка алгоритму Як тільки задача чітко поставлена і
- 23. Алгоритм повинен задовольняти вимогам, які дещо суперечать
- 24. Якщо маємо справу із завданням, рішення якого
- 25. Приклад. Один з найпростіших варіантів алгоритму для
- 26. Алгоритм ETS (вичерпний комівояжер)Вхідні дані: кількість міст
- 27. Правильність алгоритму Доведення правильності алгоритму – це один
- 28. Приклад. Алгоритм ETS настільки простий, що його
- 29. Реалізація алгоритму Цей крок може бути доволі важким.
- 30. По-друге, реалізація може виявитися складним процесом тому,
- 31. По-третє, одна справа – довести правильність конкретного
- 32. Аналіз алгоритму та його складності Причини для
- 33. Нехай А – алгоритм для розв’язку певного
- 34. Наступне позначення стандартне в багатьох математичних дисциплінах,
- 35. Математичне визначення порядку зростання функції Кажуть, що функція
- 36. Оцінка зверху
- 37. Оцінка знизу
- 38. Класи складності алгоритмівКонстантні алгоритми f(n) = O(1)
- 39. Будемо користуватися критерієм оцінки часу виконання для
- 40. Звичайно, хотілося б провести якомога точніший аналіз,
- 41. Важливо також знати, наскільки погано працює експоненційний
- 42. Приклад. Розглянемо алгоритм ETS. В задачі з
- 43. Припустимо, що у нашого комівояжера 20 міст
- 44. Необхідно підкреслити, що ступінь зростання якнайгіршого часу
- 45. 2. Якщо програма працюватиме тільки з "малими"
- 46. 3. Ефективні, але складні алгоритми можуть бути
- 47. Коли варто проводити аналіз алгоритму? Доцільно підкреслити, що
- 48. Перевірка програми Існує три аспекти перевірки програми: На
- 49. Перевірка правильності підтверджує, що програма робить саме
- 50. Міри безпеки. Легше перевіряти правильність програми, якщо
- 51. Локальні перевірки. Ряд простих тестів, або перевірок
- 52. Перевірка на неприпустимі значення. В кожному операторі,
- 53. Перевірка усіх частин програми. Перевіряйте доти, доки
- 54. Тестові дані.Значні зусилля слід направити на отримання
- 55. Перевіряйте програму на даних, що лежать на
- 56. Перевіряйте програму на даних, що виходять за
- 57. Пошук скритих помилок.Випробуйте все, що зможете придумати,
- 58. Повторна перевірка.Якщо під час перевірки виявлено помилки,
- 59. Перевірка ефективності реалізації направлена на відшукання способів
- 60. Методи підвищення ефективності програмимашинно незалежні: Арифметичні операції.Арифметичні операції
- 61. Порядок в логічних виразах.Більшість компіляторів припиняють обчислення
- 62. Профілі виконання.Один із хороших способів знаходження фрагменту
- 63. Профілі виконання корисні не тільки для перевірки
- 64. Перевірка обчислювальної складності зводиться до експериментального аналізу
- 65. Документація Насправді етап документації не є останнім в
- 66. Зовнішня документація. Являє собою дещо про програму, що
- 67. Програмна документація. Перерахуємо прийоми, якими користуються багато хороших
- 68. Слід використовувати мнемонічні імена для змінних та
- 69. Уникайте поганого або заплутаного тексу програми. Заплутаний
- 70. Уникайте нестандартних засобів версії мови. Якщо ви
- 71. Можна стверджувати, що вихідна інформація є найбільш
- 72. Розробник програми повинен допомагати користувачу, складаючи осмислені
- 73. Обслуговування Багато програмістів вважає, що не існує великих
- 74. На простоту та якість обслуговування впливають такі
- 75. 1.2. Час виконання програм Література для самостійного
- 76. На час виконання програми впливають наступні чинники:
- 77. Розглянемо, як виконуються операції додавання і множення
- 78. Приклад. Правило сум використовується для обчислення часу
- 79. Правило добутків. Якщо T1(n) і Т2(n) мають
- 80. Приклад. Визначення часу виконання програми. procedure bubble
- 81. Число елементів n, що підлягають сортуванню, може
- 82. Тепер підрахуємо час виконання умовних і циклічних
- 83. Далі розглянемо групу (2)–(6) операторів внутрішнього
- 84. Тепер перейдемо до зовнішнього циклу, який містить
- 85. Загальні правила обчислення часу виконання програми1. Час
- 86. 3. Час виконання умовних операторів складається з
- 87. 4. Час виконання циклу є сумою часу
- 88. 5. Для програм, що містять декілька процедур
- 89. Домашнє завдання Прочитати с.181-185 [2] Підготуватися до виконання практичної роботи №1.
- 90. Скачать презентанцию
Мета курсу допомогти майбутнім програмістам навчитися: Поставити та формалізувати задачу;Побудувати алгоритм, що працює;Реалізувати алгоритм як машинну програму;Оцінити ефективність алгоритму.
Слайды и текст этой презентации
Слайд 2Мета курсу
допомогти майбутнім програмістам навчитися:
Поставити та формалізувати задачу;
Побудувати
алгоритм, що працює;
Слайд 3Основна література
Ахо А., Хопкрофт Д., Ульман Д. Структуры данных и
алгоритмы / М.: Вильямс, 2000 – 384с.
Гудман С., Хидетниеми С.
Введение в разработку и анализ алгоритмов/М.: Мир, 1981 – 368 с. Ахо А., Хопкрофт Д., Ульман Д. Построение и анализ вычислительных алгоритмов / М.: Мир, 1978 – 519с.
Ковалюк Т.В. Основи програмування / К.: BHV, 2005 – 384 с.
Слайд 4Додаткова література
Кнут Д. Искусство программирования, т.3. Сортировка и поиск./ М.:
Мир, 1978 – 355 с.
Седжвик Р. Фундаментальные алгоритмы на С++ /
К.: ДиаСофт, 2001 – 688с.Гери М., Джонсон Д. Вычислительные машины и труднорешаемые задачи / М.: Мир, 1982 – 419с.
Слайд 5Структура курсу
Побудова і аналіз алгоритмів
Методи розробки алгоритмів
Основні абстрактні типи даних
Оператори
обробки множин
Оператори обробки графів
Алгоритми сортування
Методи аналізу рекурсивних алгоритмів
Слайд 6Оцінювання роботи
Практичні роботи (по 10 балів):
Побудова і аналіз алгоритмів
Методи
розробки алгоритмів
Абстрактні типи даних
Оператори обробки множин
Оператори обробки графів
Алгоритми сортування
Контрольні роботи
– 40 балів
Слайд 101.1. Від задачі до програми
Література для самостійного читання:
Постановка задачі с.16
[2]
Побудова моделі с.17 [2]
Розробка алгоритму с.19 [2]
Правильність алгоритму с.21 [2]
Реалізація алгоритму с.22 [2]
Аналіз алгоритму
та його складності с.23 [2]Перевірка програми с.26, с.197 [2]
Документація с.28, с.216 [2]
![1.1. Від задачі до програми Література для самостійного читання:Постановка задачі с.16 [2] Побудова моделі с.17 [2]Розробка алгоритму с.19 [2]Правильність алгоритму с.21 [2] Реалізація](/img/thumbs/59fa3d15600e85e6575a661c24686b25-800x.jpg "ТЕОРІЯ АЛГОРИТМІВ 1.1. Від задачі до програми Література для самостійного читання:Постановка задачі с.16 [2] Побудова")
Слайд 11 Постановка задачі
Щоб зрозуміти задачу, потрібно точно її сформулювати. Ця умова
сама по собі не є достатньою для розуміння задачі, але
є абсолютно необхідною.Зазвичай процес точного формулювання задачі зводиться до постановки правильних питань.
Чи зрозуміла термінологія, що використовується в попередньому формулюванні?
Що дано?
Що потрібно знайти?
Як визначити розв’язок?
Яких даних не вистачає та чи всі вони потрібні?
Можливо, якісь дані, що вже маємо, для розв’язку не знадобляться?
Які зроблено припущення (спрощення)?
Слайд 12 Приклад
Андрій – агент по продажу кондиціонерів (комівояжер); на його
території 20 міст, розкиданих по всій області. Компанія відшкодовує йому
тільки 50% вартості ділових автомобільних поїздок. Андрій підрахував, скільки йому буде коштувати переїзд на машині між кожними двома містами на його території. Йому, звичайно, хотілось би зменшити свої дорожні витрати.
Слайд 13 Що дано?
Вхідна інформація задана у вигляді переліку міст на
території Андрія та відповідної матриці вартостей, тобто двомірного масиву з
елементами cij, що дорівнюють вартості переїзду з міста i в місто j. В даному випадку матриця вартостей має 20 рядків та 20 стовпчиків.
Слайд 14 Що ми хочемо знайти?
Ми хочемо допомогти Андрію знизити його
дорожні витрати. Це звучить дещо розпливчасто, тому що питання про
те, як виглядатиме розв’язок, залишилось не вирішеним.Обдумавши ситуацію, ми прийдемо до висновку, що нічого не можемо зробити без додаткової інформації від Андрія. Чи має Андрій в одних містах більше покупців, ніж в інших? Якщо так і якщо є якісь особливі покупці, то Андрій, можливо, захоче відвідувати якісь міста частіше. Можуть бути і такі міста, в котрі Андрій навмисно не поїде, а заїде туди, коли опиниться в сусідньому місті.
Іншими словами, нам треба знати більше про пріоритети Андрія і враховувати переваги при складанні графіку поїздок.
Слайд 15 Тому ми повертаємося до Андрія і вимагаємо в нього додаткову
інформацію. Він повідомляє, що хотів би мати маршрут, який починається
та закінчується в його базовому місті та проходить по одному разу через усі міста на його території.Звідси, нам потрібно скласти список міст, в якому кожне місто зустрічається тільки один раз, за винятком базового міста, котре стоїть в списку першим та останнім. Порядок міст в цьому списку являє собою маршрут, по якому Андрій повинен об’їжджати міста на своїй території. Сума вартостей проїзду між кожними двома послідовними містами списку – це загальна вартість маршруту, представленого списком. Ми розв’яжемо задачу Андрія, якщо дамо йому список з найменшою можливою загальною вартістю.
Слайд 16 Побудова моделі
Вибір моделі суттєво впливає на решту етапів побудови алгоритму
для розв’язку задачі. Нажаль, неможливо запропонувати набір правил, що автоматизують
стадію моделювання, але існує кілька корисних керуючих принципів.Приступаючи до розробки моделі, слід задати принаймні два основних питання:
Які математичні структури найкраще підходять для задачі?
Чи існують розв’язані аналогічні задачі?
Слайд 17 На вибір відповідної математичної структури будуть впливати такі фактори:
1) Обмеженість наших
знань відносно невеликою кількістю структур;
2) Зручність представлення;
3) Простота обчислень;
4) Корисність різних операцій, пов’язаних
з структурами, що розглядаються.
Слайд 18 Зробивши пробний вибір математичної структури, задачу слід переформулювати в термінах
відповідних математичних об’єктів. Це буде одна з можливих моделей, якщо
ми зможемо ствердно відповісти на такі питання, як:Чи вся важлива інформація задачі добре описана математичними об’єктами?
Чи існує математична величина, що асоціюється з шуканим результатом?
Чи виявили ми які-небудь корисні відношення між об’єктами моделі?
Чи можемо ми працювати з моделлю? Чи зручно з нею працювати?
Слайд 19 Приклад.
Повернемося до задачі Андрія. Чи розв’язували ми раніше аналогічні
задачі? Усім нам траплялися задачі вибору шляху по картам доріг
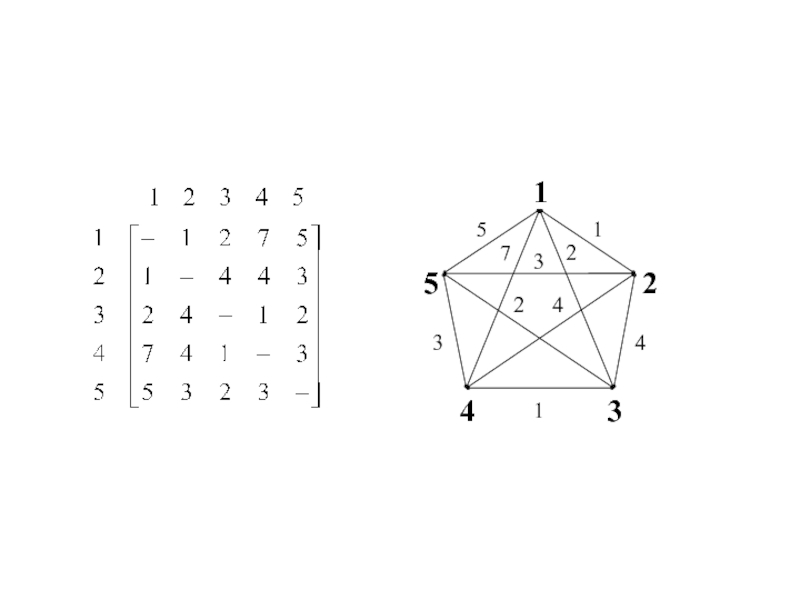
або в лабіринті. Чи можемо ми прийти до зручного представлення нашої задачі на зразок карти? Так, можемо. Для цього використаємо граф, вершини якого будуть позначати міста, а зважені ребра – шляхи між ними. Для простоти покладемо що у Андрія тільки 5 міст. Припустимо також, що вартість проїзду з міста i в місто j така сама, як і з міста j в місто i, хоча це не обов’язково. Для зручності замість назв міст використовуємо цифри.
Слайд 21 Що ми шукаємо в задачі?
В термінах теорії графів список
міст визначає замкнений цикл, що починається з базового міста і
повертається в нього ж після проходження кожного міста по одному разу. Такий цикл називається гамільтоновим, а для розв’язку задачі такого роду обхід міст будемо називати туром. Вартість туру визначається як сума ваг всіх пройдених ребер. Задача розв’язана, якщо ми можемо знайти тур з найменшою вартістю.
Слайд 22 Розробка алгоритму
Як тільки задача чітко поставлена і для неї побудована
модель, можна приступити до розробки алгоритму її розв’язку.
Вибір методу
розробки, що часто залежить від вибору моделі, може значно вплинути на ефективність алгоритму розв’язку. Два різних алгоритми можуть бути правильними, але дуже різними по ефективності.Тому програмісти повинні бути обізнані не тільки з методами побудови швидких програм, але і знати, коли їх слід застосовувати (бажано з мінімальними зусиллями програмістів).
Слайд 23 Алгоритм повинен задовольняти вимогам, які дещо суперечать одна одній:
бути
простим для розуміння, перекладу в програмний код і наладки;
ефективно
використовувати комп'ютерні ресурси і виконуватися по можливості швидко. Якщо написана програма повинна виконуватися тільки кілька разів, то перша вимога найбільш важлива. Вартість робочого часу програміста зазвичай значно перевищує вартість машинного часу виконання програми, тому вартість програми оптимізується за вартістю написання (а не виконання) програми.
Слайд 24 Якщо маємо справу із завданням, рішення якого вимагає значних обчислювальних
витрат, то вартість виконання програми може перевищити вартість написання, особливо
якщо програма повинна виконуватися багатократно. Тому, з фінансової точки зору, доцільнішим може стати складний комплексний алгоритм (у надії, що результуюча програма буде виконуватися істотно швидше, ніж простіша програма).Але і в цій ситуації розумніше спочатку реалізувати простій алгоритм, щоб визначити, як повинна поводитися складніша програма. При побудові складної програмної системи бажано реалізувати її простий прототип, на якому можна провести необхідні вимірювання і змоделювати її поведінку в цілому, перш ніж приступати до розробки остаточного варіанту.
Слайд 25 Приклад.
Один з найпростіших варіантів алгоритму для задачі Андрія. Базовому
місту приписуємо номер n. Кожен тур однозначно відповідає перестановці цілих
чисел 1, 2, … , n–1, його легко прослідкувати на графі та порахувати його вартість. Наприклад, вартість туру 5-1-2-3-4-5 (n=5) дорівнює 5+1+4+1+3=14. Можна розв’язати задачу, генеруючи всі перестановки перших n–1 цілих додатних чисел. Для кожної перестановки будуємо відповідний тур та рахуємо його вартість. Оброблюючи таким чином всі перестановки, запам’ятовуємо тур, який на поточний момент має найменшу вартість. Якщо знаходимо тур з меншою вартістю, то подальші порівняння робимо з цим туром.
Слайд 26 Алгоритм ETS (вичерпний комівояжер)
Вхідні дані: кількість міст N, матриця вартостей
C.
Вихідні дані: порядок обходу міст TOUR з найменшою вартістю MIN.
Крок
0. Встановлення початкових значеньTOUR=0, MIN=∞
Крок 1. Генерування всіх перестановок
For i=1 to (N-1)! do
Крок 2. Отримання нової i-ої перестановки P (підалгоритм)
Крок 3. Побудова тура, що відповідає перестановці T(P) (підалгоритм) та обчислення його вартості COST(T(P)) (підалгоритм)
Крок 4. Порівняння поточного тура з мінімальним та заміна мінімального при потребі.
If COST(T(P))
Слайд 27 Правильність алгоритму
Доведення правильності алгоритму – це один з найважчих, а
іноді й дуже втомлюючих етапів створення алгоритму.
Найбільш загальна методика доведення
правильності алгоритму полягає в наступному. Припустимо, що алгоритм описано у вигляді послідовності кроків. Потрібно запропонувати деяке обґрунтування правомірності для кожного кроку (зокрема, може знадобитися лема про умови, що діють до та після пройденого кроку).
Потрібно запропонувати доведення кінцевості (результативності) алгоритму, при цьому будуть перевірені всі підходящі вхідні дані і отримані всі підходящі вихідні дані.
Слайд 28 Приклад.
Алгоритм ETS настільки простий, що його правильність легко довести.
Оскільки перевіряється кожен тур, повинен бути перевіреним і тур з
мінімальною вартістю; як тільки до нього дійде черга, він буде збережений. Він не буде відкинений – це може статися лише в тому випадку, якщо існує тур з меншою вартістю. Алгоритм повинен закінчити роботу, оскільки число турів, які потрібно перевірити, кінцеве. Подібний метод доведення відомий як «доведення повним перебором випадків»; це найгрубіший із методів доведення.Правильність алгоритму ще нічого не говорить про його ефективність. Вичерпні алгоритми рідко бувають хорошими у всіх відношеннях.
Слайд 29 Реалізація алгоритму
Цей крок може бути доволі важким.
По-перше, складність є
в тому, що дуже часто окремо взятий крок алгоритму може
бути виражений у формі, яку важко перевести безпосередньо в конструкції мови програмування. Наприклад, один із кроків алгоритму може бути записаний у вигляді, що потребує цілої підпрограми для його реалізації.
Слайд 30 По-друге, реалізація може виявитися складним процесом тому, що перед написанням
програми потрібно побудувати цілу систему структур даних для представлення важливих
аспектів моделі, що використовується. Щоб це зробити, необхідно відповісти, наприклад, на такі питання:Які є основні змінні?
Яких вони типів?
Скільки потрібно масивів і якої вони розмірності?
Чи є сенс використовувати зв’язні списки?
Які потрібні підпрограми (можливо, вже розроблені)?
Якою мовою програмування користуватися?
Слайд 31 По-третє, одна справа – довести правильність конкретного алгоритму, описаного в
словесній формі, інша справа – довести, що дана машинна програма,
яка припустимо є реалізацією цього алгоритму, також правильна.Крім того, конкретна програмна реалізація може суттєво впливати на вимоги до пам’яті та на швидкодію алгоритму, що теж потрібно врахувати при виборі реалізації алгоритму.
Слайд 32 Аналіз алгоритму та його складності
Причини для аналізу алгоритму:
практичні
необхідність отримання оцінок або границь для обсягу пам’яті або часу
роботи; теоретичні
необхідність порівняння алгоритмів (за певним критерієм);
необхідність виявлення найбільш ефективних алгоритмів (за набором критеріїв);
необхідність оцінки доцільності подальшого покращення алгоритму.
Слайд 33 Нехай А – алгоритм для розв’язку певного класу задач, а
n – розмірність окремої задачі цього класу. В багатьох задачах
теорії графів, наприклад, n – просто скаляр, рівний числу вершин графа. В загальному випадку n може бути масивом або довжиною послідовності, що вводиться.Визначимо fA(n) як робочу функцію, що дає верхню границю для максимального числа основних операцій (додавання, порівняння і т.д.), які повинен виконати алгоритм А для розвозку будь-якої задачі розмірності n.
Слайд 34 Наступне позначення стандартне в багатьох математичних дисциплінах, в тому числі
в аналізі алгоритмів.
Функцію f(n) визначають як O[g(n)] і говорять,
що вона порядку g(n) для великих n, якщоФункція h(n) є o[z(n)] для великих n, якщо
Ці символи читаються, відповідно, як «O велике від n» та «o мале від n». Інтуїтивно, якщо f(n) є O[g(n)], то ці дві функції зростають з однаковою швидкістю при n→∞. Якщо f(n) є о[g(n)], то g(n) зростає набагато швидше, ніж f(n).
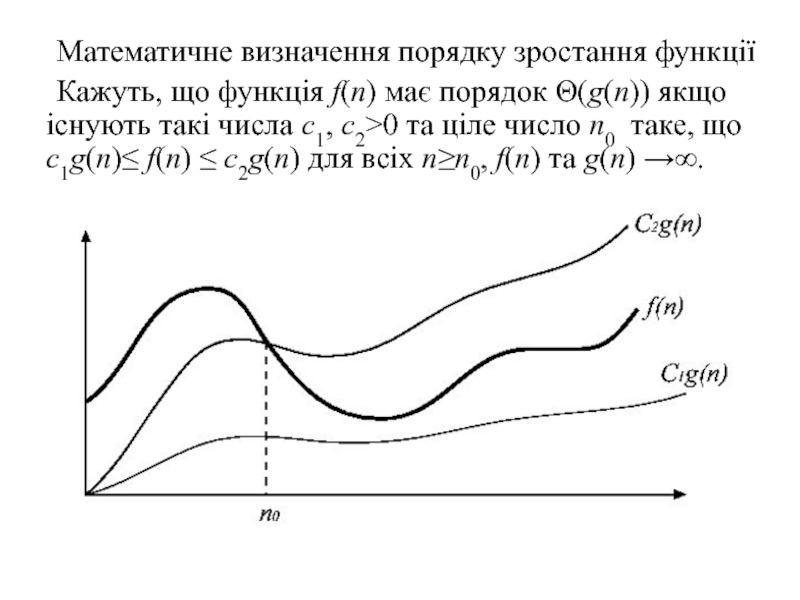
Слайд 35 Математичне визначення порядку зростання функції
Кажуть, що функція f(n) має порядок
(g(n)) якщо існують такі числа с1, с2>0 та ціле число
n0 таке, що с1g(n)≤ f(n) ≤ с2g(n) для всіх n≥n0, f(n) та g(n) →∞.
Слайд 36 Оцінка зверху f(n) = O[g(n)]
Існує
число с>0 та ціле число n0 таке, що
сg(n) ≥
f(n) для всіх n≥n0, f(n) та g(n) →∞.![Оцінка зверху f(n) = O[g(n)] Існує число с>0 та ціле число n0 таке,](/img/thumbs/e288d71800c9ebb984b9146206f6cd71-800x.jpg "ТЕОРІЯ АЛГОРИТМІВ Оцінка зверху f(n) = O[g(n)] Існує число с>0 та ціле")
Слайд 37 Оцінка знизу f(n) =
о[g(n)]
Існує число с>0 та ціле число n0 таке, що
сg(n)
≤ f(n) для всіх n≥n0, f(n) та g(n) →∞.![Оцінка знизу f(n) = о[g(n)] Існує число с>0 та ціле число n0](/img/thumbs/0ae2d80e38e52ed46405ddf3735c1d0e-800x.jpg "ТЕОРІЯ АЛГОРИТМІВ Оцінка знизу f(n) = о[g(n)] Існує число с>0 та")
Слайд 38 Класи складності алгоритмів
Константні алгоритми f(n) = O(1) – час їх
виконання обмежено константою, яка не залежить від розміру вхідних даних;
Логарифмічні
алгоритми f(n) = O(log n) – основу логарифму можна не враховувати, оскільки перехід до іншої основи є множенням на константу;Лінійні алгоритми f(n) = O(n);
Квадратичні алгоритми f(n) = O(n2);
Поліноміальні алгоритми f(n) = O(nk);
Експоненційні алгоритми f(n) = O(an); відмітьте, що n!= о(2n) і n! = O(nn).
Слайд 39 Будемо користуватися критерієм оцінки часу виконання для оцінки якості алгоритму
А.
Цей критерій заснований на часі роботи в найгіршому випадку,
але аналогічний критерій може бути визначений також для середнього часу роботи. «Експериментальна» основа критерію якості заключається в тому, що обчислювальні машини більш-менш здатні сприймати поліноміальні алгоритми для великих задач, а на експоненційних алгоритмах вони швидко «задихаються».
Слайд 40 Звичайно, хотілося б провести якомога точніший аналіз, тобто знати якомога
більше про функцію fA(n). Ми б краще уявляли собі дію
алгоритму А, якби знали, що fA(n)=2.5n2+3.7n-5.2, ніж якби нам було відомо лише, що fA(n)=O(n2). Такі детальні відомості про алгоритм можна отримати тільки з конкретної реалізації.Точні коефіцієнти fA(n) в загальному випадку залежать від реалізації, в той час як характеристика O(n2) властива алгоритму, тобто не залежить від особливостей реалізації.
Слайд 41 Важливо також знати, наскільки погано працює експоненційний алгоритм. Існує багато
важливих задач, для яких на даний момент відомі лише експоненційні
алгоритми. Ці задачі мусимо розв’язувати, бо вони мають велику практичну значимість. Якщо відомі лише експоненційні алгоритми, то хотілось би користуватися найбільш ефективними з них. Очевидно, що слід віддати перевагу алгоритму, що розв’язує задачу розмірності n за О(2n) кроків, перед алгоритмами, що розв’язують її за О(n!) або О(nn) кроків.
Слайд 42 Приклад. Розглянемо алгоритм ETS.
В задачі з n містами потрібно
вичерпно перерахувати перестановки перших n-1 додатних цілих чисел. Кількість таких
перестановок (n-1)! Навіть якщо потрібен лише один крок для кожної такої перестановки (а це груба недооцінка), ця частина алгоритму вже вимагатиме О((n-1)!) кроків. Як тільки згенеровано перестановку, можна знайти відповідний тур та його вартість за О(n) кроків. Тому будь-яка верхня границя для загального часу роботи повинна бути принаймні О(n!).
Слайд 43 Припустимо, що у нашого комівояжера 20 міст і що у
нас є феноменальний підалгоритм, що згенерує перестановку за один крок.
Припустимо також, що маємо швидкодіючу машину, котра виконує кожний елементарний крок (додавання, порівняння, пошук елемента матриці) за 10-7с. Тоді, оскільки 20!≈2∙1018, розв’язок задачі займе трохи менше 70 століть. Звичайно, це досить сильно підірве нашу довіру до алгоритму ETS.
Слайд 44 Необхідно підкреслити, що ступінь зростання якнайгіршого часу виконання - не
єдиний або найважливіший критерій оцінки алгоритмів і програм.
1. Якщо
створювана програма буде використана тільки кілька разів, тоді вартість написання і наладки програми домінуватиме в загальній вартості програми, тобто фактичний час виконання не дасть істотного впливу на загальну вартість. В цьому випадку слід віддати перевагу алгоритму, найбільш простому для реалізації. 
Слайд 452. Якщо програма працюватиме тільки з "малими" вхідними даними, то
степінь зростання часу виконання матиме менше значення, ніж константа, присутня
у формулі часу виконання.Разом з тим і поняття "менших" вхідних даних залежить від точного часу виконання конкуруючих алгоритмів. Існують алгоритми, такі як алгоритм цілочисельного множення, асимптотично найефективніші, але які ніколи не використовують на практиці навіть для великих завдань, оскільки їх константи пропорційності значно перевершують подібні константи інших, більш простих і менш "ефективних" алгоритмів.
Слайд 463. Ефективні, але складні алгоритми можуть бути небажаними, якщо готові
програми підтримуватимуть особи, що не беруть участь в написанні цих
програм.4. Відомо декілька прикладів, коли ефективні алгоритми вимагають таких великих об'ємів машинної пам'яті (без можливості використання повільніших зовнішніх засобів зберігання), що цей чинник зводить нанівець перевагу "ефективності" алгоритму.
5. У чисельних алгоритмах точність і стійкість алгоритмів не менш важливі чим їх часова ефективність.
Слайд 47 Коли варто проводити аналіз алгоритму?
Доцільно підкреслити, що до етапів повної
побудови алгоритму не треба відноситись як до чогось незмінного. Деякі
етапи можуть виконуватись одночасно з іншими, деякі можуть навіть бути пропущеними. Якщо є хороша модель, то, мабуть, не має потреби будувати іншу. Звичайно, неможливо довести правильність алгоритму до того, як він буде розроблений, але, можливо, краще провести деякий аналіз процесу розробки алгоритму до того, як почати його реалізовувати. Це тим більш так, якщо є привід припускати, що алгоритм буде експоненційним. Деякий аналіз на стадії розробки може підказати, як зробити алгоритм більш ефективним. І, нарешті, етапи процесу побудови можуть буди з вигодою переглянуті після того, як вони вже вважаються завершеними. Наприклад, фази аналізу та перевірки можуть забезпечити цінний зворотній зв'язок з етапами розробки та реалізації.
Слайд 48 Перевірка програми
Існує три аспекти перевірки програми:
На правильність
На ефективність реалізації
На
обчислювальну складність
Разом узяті ці перевірки спрямовані на отримання експериментальної відповіді
на питання: чи працює алгоритм? Наскільки добре він працює? 
Слайд 49 Перевірка правильності підтверджує, що програма робить саме те, для чого
вона була призначена. Важливо зрозуміти, що математична бездоганність алгоритму не
гарантує правильності перекладу його в програму. Аналогічно ні відсутність діагностичних повідомлень компілятора, ні «розумний вигляд» результатів прогону не дають достатньої гарантії правильності програми. Це часто ілюструють приклади багатьох програм, які працюють місяці або навіть роки до того як в них виявляються помилки.Далі перераховано, на що варто звернути увагу при перевірці правильності програми.
Слайд 50 Міри безпеки.
Легше перевіряти правильність програми, якщо більш ранні кроки
її побудови були ретельно організовані та виконані. В значній мірі
розвиток структурного програмування згори-вниз був мотивований цими міркуваннями.Плануйте перевірку програми в процесі її розробки, думайте про те, як можна перевірити кожен модуль і які слід використати для цього дані, ще в процесі його написання.
Плануйте наперед зміни, які передбачаються в програмі в майбутньому. Задайтеся запитанням, які саме зміни найімовірніше доведеться зробити? Здорова турбота про універсальність програми допоможе уникнути витратних переробок цілих сегментів написаної програми.
Слайд 51 Локальні перевірки.
Ряд простих тестів, або перевірок може бути виконаний
вручну.
Перевіряйте відповідність між оператором алгоритму або блок-схеми і його реалізацією
в програмі. Виконайте локальні перевірки описів усіх змінних, міняючи всі входження змінної, ім’я якої було змінене. Перевірте відповідність розмірностей масивів. Встановіть оператори наладки або друку. Виконуйте всі зміни відразу ж, як тільки в них виникла необхідність, або принаймні відмічайте їх, інакше їх легко забути.
Слайд 52Перевірка на неприпустимі значення. В кожному операторі, якщо це можливо,
розгляньте можливість появи неприпустимого значення деякої змінної і спробуйте визначити
причину, з якої це могло б трапитися. Переконайтеся, що всі змінні ініціалізовані правильно, наприклад, при кожному виклику підпрограми. Переконайтеся, що індекси не можуть приймати занадто малі або занадто великі значення. Крім того перевірте, щоб неприпустимі значення не могли бути внесені зовні в підпрограму.Перевірка на нескінчені цикли. Спробуйте визначити, чи існує шлях, по якому програма могла б потрапити в нескінчений цикл.
Слайд 53 Перевірка усіх частин програми.
Перевіряйте доти, доки кожен присутній в
програмі оператор не буде давати правильний результат. Зокрема, перевірте кожну
гілку і кожну умову помилки хоча б один раз. Намагайтеся перевірити якомога більше різних шляхів через програму. Зверніть увагу на те, що програми із структурою дерева мають набагато менше шляхів, ніж програми із складними структурами циклів.
Слайд 54 Тестові дані.
Значні зусилля слід направити на отримання хороших даних для
перших же тестів. Початковий набір тестових даних повинен покривати широкий
діапазон часткових випадків; обов’язково повинні бути відомі вірні відповіді. Потрібно включати дані, що перевіряють усі умови помилок. Можна також пропустити через програму які-небудь беззмістовні дані, щоб подивитися, чи вірно вони оброблюються.Уникайте прогону даних, які по суті вимагають, щоб система знову і знову виконувала те ж саме. Також намагайтеся уникати тестових даних, відповіді на які не можна перевірити. Випадкові дані зазвичай мають обидва ці недоліки.
Слайд 55Перевіряйте програму на даних, що лежать на границях допустимих діапазонів.
Якщо діапазон для вхідних даних визначається розміром задачі, зробіть окрему
спробу перевірити дуже великі і дуже маленькі задачі. Зверніть особливу увагу на нульові випадки. Наприклад, порожні рядки, графи без вершин або ребер, нульові матриці, тощо. Якщо програмою будуть користуватися часто, то можете бути впевнені, що усі можливі крайні випадки рано чи пізно проявляться. Перевірте їх вчасно.
Слайд 56Перевіряйте програму на даних, що виходять за межі припустимого діапазону
вхідних даних. Остерігайтеся небезпечної ситуації, коли програма видає правдоподібні, але
невірні результати. Якщо доступна інша програма, що розв’язує цю ж задачу, використайте її для контролю програми, що перевіряється. Хоча це і мало імовірно, майте на увазі, що обидві програми можуть виявитися неправильними.Слід також витратити деякі зусилля, щоб перевірити програму на реальних даних, якщо передбачається її практичне використання. Може виявитися необхідною співпраця з потенційними користувачами.
Слайд 57 Пошук скритих помилок.
Випробуйте все, що зможете придумати, щоб виявити в
програмі помилку. Якщо можливо, попросіть кого-небудь іншого зробити це. Свіжий
погляд може бути саме тим, що потрібно для локалізації непоміченої вами помилки.Час, що необхідний для перевірки.
Перевірка вимагає зазвичай суттєвої кількості часу, і не слід її пришвидшувати. Зарезервуйте для наладки досить часу.
Слайд 58 Повторна перевірка.
Якщо під час перевірки виявлено помилки, потрібно зробити зміни,
щоб їх виправити. Слід потурбуватися про те, щоб не нагромаджувати
одне виправлення на інше. Потрібно встановити всі місця програми, на які впливає дана помилка. Переконайтеся, що виправлення однієї помилки не породжує нових. З цією метою можна було б зберегти старі тестові дані і використати їх для повторної перевірки програми.Коли припинити перевірку?
Для будь-якої конкретної програми відповідь залежить від її можливого застосування та від рівня впевненості, якого бажає досягти програміст. Часто питання вирішується виходячи з наявних часу та коштів.
Слайд 59 Перевірка ефективності реалізації направлена на відшукання способів змусити правильну програму
працювати швидше або витрачати менше пам’яті. Щоб покращити програму, переглядаються
результати етапу реалізації в процесі побудови алгоритму.Така перевірка виявляється втратою часу для простих програм, або для програм, якими будуть користуватися рідко, але дуже корисна для програм, якими будуть користуватися часто.
Доцільно застерегти, що гранично ефективне кодування може порушити ясність програми і зробити перевірку її правильності набагато важчою. Взагалі слід уникати змін, що загрожують зрозумілості, якщо вони не можуть бути виправдані суттєвою економією часу або пам’яті.
Слайд 60 Методи підвищення ефективності програми
машинно незалежні:
Арифметичні операції.
Арифметичні операції додавання та віднімання
виконуються швидше ніж множення та ділення. Зведення в степінь –
найповільніша операція. Крім того, цілочисельна арифметика за звичай швидше арифметики дійсних чисел. Таким чином величину X2 швидше обрахувати як X*X, а X+X може виявитися швидше ніж 2.0*X.Надлишкові обчислення.
Якщо складний вираз зустрічається більше ніж в одному місці обчислюйте його один раз та надавайте обчислене значення змінній.
Слайд 61 Порядок в логічних виразах.
Більшість компіляторів припиняють обчислення логічних виразів як
тільки результат отримано. Наприклад в виразі (A or B or
C), обчислення буде припинено, як тільки буде знайдено значення TRUE. Певний час можна зекономити, розмістивши A, B, C так, щоб A найімовірніше виявилося істинним, B - наступним по величині ймовірності, а C - з найменшою імовірністю.Виключення, розгортання та спрощення циклів.
Найбільші можливості підвищення ефективності виконання криються в сегментах програми, що часто повторюються. Такі сегменти майже завжди мають форму циклів. Одним з методів скорочення витрат часу на цикли є скорочення кількості повторів.
Слайд 62 Профілі виконання.
Один із хороших способів знаходження фрагменту програми, що є
найбільш ресурсоємним, складається в побудові профілю виконання програми. Робота програми
контролюється набором таймерів та лічильників і видається лістинг, який показує, скільки разів виконався кожний оператор і скільки одиниць часу витрачено на виконання кожного оператора. Зазвичай в засобах наладки є бібліотечні програми, що допомагають згенерувати такі профілі. Якщо ж немає готового пакета програм для побудови профілю, неважко зібрати грубі профілі.Статистичні дослідження з використанням профілів виконання виявили примітний факт, що приблизно 5% обсягу більшості програм потребують приблизно 50% часу виконання.
Слайд 63Профілі виконання корисні не тільки для перевірки ефективності реалізації, але
і для інших двох типів перевірки.
При перевірці правильності ці
профілі можна використовувати для того, щоб побачити які сегменти програми виконуються, а які ні. Таким чином, профілі можуть допомогти перевірити, чи всі частини програми протестовані. Профілі також корисні для проведення експериментального детального аналізу складності на основі послідовного перегляду операторів.
Слайд 64 Перевірка обчислювальної складності зводиться до експериментального аналізу складності алгоритму або
до експериментального порівняння двох чи більше алгоритмів, що розв’язують одну
і ту ж саму задачу. Крім того, перевірки цього типу застосовуються для доповнення теоретичного аналізу алгоритму. Якщо теоретичний аналіз занадто важко провести, необхідно все ж накопичити певний обчислювальний досвід роботи з цим алгоритмом. Цей досвід можна використовувати наприклад, для передбачення тривалості роботи програми на певному наборі вхідних даних. Результати експериментального аналізу рідко виявляються вичерпними, тому не слід виходити за розумні межі при їх інтерпретації.
Слайд 65 Документація
Насправді етап документації не є останнім в процесі повної побудови
алгоритму. Зокрема, він не складається в додаванні коментарів в програму,
коли ви закінчили решту робіт. Процес документації має переплітатися з усім процесом побудови алгоритму, і особливо з етапами розробки та реалізації.Документація включає в себе всю інформацію і допомагає пояснити, що робиться в програмі, а саме: блок-схеми, описи сходинок в побудові згори-вниз, допоміжні доведення правильності, результати тестування, детальні описи формату вхідних та вихідних даних та інше.
Для всіх програм, крім найпростіших, текст повинен супроводжуватися зовнішньою і/або внутрішньою (програмною) документацією.
Слайд 66 Зовнішня документація.
Являє собою дещо про програму, що не міститься в
самій програмі. Вона часто виконується у вигляді керівництва для користувача
або технічного звіту. В залежності від розміру та складності програми зовнішня документація може набувати різних форм:Блок-схеми
Інструкції користувача
Зразки вхідних і вихідних даних
Повний опис побудови згори-вниз
Словесний опис алгоритму
Посилання на джерела інформації
Довідники по іменам змінних та підпрограм, з вказанням їх ролей в даній програмі
Обговорення різноманітних особливостей (наприклад, результатів перевірки, обмежень, історії виправлень).
Слайд 67 Програмна документація.
Перерахуємо прийоми, якими користуються багато хороших програмістів.
Коментарі повинні бути
правильними та інформативними.
Пишіть коментарі одночасно з текстом програми. Ця
практика допомагає об’єднати документацію етапів розробки і реалізації. Корисні коментарі часто вдається отримати прямо із блок-схем або словесного тексту алгоритму. Якщо вони написані одночасно з текстом програми, вони з більшою імовірністю акуратно відображають логічні етапи програми, ніж якщо їх писати пізніше. Звичайно, було б непогано переглянути усю документацію після завершення розробки програми. 
Слайд 68Слід використовувати мнемонічні імена для змінних та підпрограм. Вони повинні
натякати на їх функцію в алгоритмі. Ця практика сприяє самодокументуванню
тексту програми.Починайте кожну програму з прологу. Повідомляйте читачу корисну інформацію на початку кожної програми та підпрограми. Пролог може містити:
Заголовок: ім’я автора, дату останньої зміни, тощо.
Короткий опис, того що робить програма і можливо того, яким чином вона це робить (принаймні вказівники на джерела інформації).
Список підпрограм, що використовуються з коротким описом мети кожної із них.
Список та опис всіх змінних, призначення яких не очевидне з першого погляду.
Інформацію про реакцію при виявленні помилкових ситуацій.
Інформацію про необхідні вхідні дані та вигляд результатів.
Слайд 69Уникайте поганого або заплутаного тексу програми. Заплутаний текст породжує помилки
і вимагає додаткової документації. Не намагайтеся компенсувати такий текст програми
великою кількістю коментарів, краще перепишіть програму.Правила чіткого оформлення програми:
Впорядковуйте оголошення змінних та масивів в деякій логічній послідовності або в алфавітному порядку.
Виділяйте окремим відступом від початку рядка фрагменти програми у відповідності до логічних рівнів. Особливо після операторів «Умова» та «Цикл».
Виділяйте відступом від початку рядку коментарі та відділяйте їх від тексту програми порожніми рядками.
Користуйтеся пробілами для полегшення читання програми, наприклад, в виразах.
Довгі вирази розбивайте на частини. Уникайте логічних або арифметичних виразів, що виходять за межі екрану.
Слайд 70Уникайте нестандартних засобів версії мови. Якщо ви передбачаєте, що програма
повинна використовуватися широким колом користувачів, обов’язково вкажіть всі нестандартні засоби,
що в ній задіяні, і якщо можливо, то чим їх можна замінити.Описуйте правильно всі вхідні та вихідні дані. Документація повинна давати користувачеві всю необхідну інформацію для успішного введення даних. Цю інформацію можна включити в програму, якщо вона ще не перевантажена документацією. Громіздкі специфікації вхідних даних слід розміщувати в керівництві користувача, а в пролозі повинно бути явне посилання на цей документ.
Слайд 71Можна стверджувати, що вихідна інформація є найбільш важливим документом будь-якої
програми, оскільки вона може виявитися єдиним документом, який бачать користувачі.
Розробник програми повинен намагатися зробити всю вихідну інформацію очевидною.Програміст повинен піклуватися про користувача. Слід роздруковувати вхідні дані в зручному для читання вигляді – це дає користувачу можливість іще раз перевірити вхідну інформацію, а програмісту забезпечує більш повний запис прогону.
Слайд 72Розробник програми повинен допомагати користувачу, складаючи осмислені повідомлення про помилки.
Слід намагатися передбачити можливі неприємності і приготуватися до появи помилок,
оскільки вони виникнуть рано чи пізно. Особливу увагу слід приділити можливим помилкам у вхідних даних і виродженим випадкам (наприклад, циклам, які нічого не роблять при даній вхідній інформації), вхідним масивам і змінним, значення яких занадто малі або занадто великі.Однією із найнудніших і непривабливих частин етапу реалізації і документації є робота по підготовці інтерфейсів. Однак, цю роботу слід виконувати ретельно, оскільки, невдалий інтерфейс компрометує всю програму.
Слайд 73 Обслуговування
Багато програмістів вважає, що не існує великих програм, вільних від
помилок або повністю протестованих. Виправляти такі програми важко, якщо вони
були документовані погано. Існує багато інших причин, коли програми потрібно оновлювати, розвивати або модифікувати з часом. Ця діяльність відноситься до категорії обслуговування програми. Це важлива робота, що збільшує час корисного життя програми.
Слайд 74 На простоту та якість обслуговування впливають такі фактори:
Програми, які дуже
вишукані, компактні, ефективні та швидкі, зазвичай важче обслуговувати. Краще пожертвувати
частиною швидкості програми для досягнення простоти обслуговування.Всі роботи по обслуговуванню будь-яких програм слід виконувати над копією програми, а оригінал старої версії слід зберігати недоторканим на протязі значного проміжку часу.
Всі зміни в ході робіт по обслуговуванню слід ретельно фіксувати. Стару документацію слід оновлювати; це стосується не тільки опису змін, але й видалення застарілої і неправильної документації. Будь-яку зовнішню документацію бажано забезпечувати додатками, які містять детальний опис роботи по обслуговуванню, включаючи таку інформацію, як дати змін, їх причини, тощо.
Слайд 751.2. Час виконання програм
Література для самостійного читання:
Асимптотичні співвідношення
с.28-32 [1]
Обчислення часу виконання програм
с.32-37 [1]Обчислення часу виконання
рекурсивних процедур с.265-272 [1]
Повний приклад с.181-185 [2]
![1.2. Час виконання програм Література для самостійного читання:Асимптотичні співвідношення с.28-32 [1]Обчислення часу виконання програм](/img/thumbs/97be4907692b24808d36ed7832c187f8-800x.jpg "ТЕОРІЯ АЛГОРИТМІВ 1.2. Час виконання програм Література для самостійного читання:Асимптотичні співвідношення с.28-32")
Слайд 76 На час виконання програми впливають наступні чинники:
Введення початкової інформації
в програму (зокрема, її розмір).
Якість скомпільованого коду програми.
Машинні
інструкції (природні і прискорюючі), використані для виконання програми. Складність алгоритму відповідної програми (кількість кроків алгоритму).
Слайд 77 Розглянемо, як виконуються операції додавання і множення з використанням О-символіки.
Правило сум. Нехай T1(n) і Т2(n) - час виконання двох
програмних фрагментів Р1 і Р2 , T1(n) має ступінь зростання O(f(n)), а Т2(n) - O(g(n)). Тоді T1(n)+Т2(n), тобто час послідовного виконання фрагментів Р1 і Р2, має ступінь зростання O(max(f(n), g(n))). Для доказу цього пригадаємо, що існують константи с1, с2, n1 і n2 такі, що при n≥n1 виконується нерівність T1(n)≤с1f(n), і, аналогічно, Т2(n)≤с2g(n), якщо n≥n2. Хай n0=max(n1, n2). Якщо n≥n0, то, очевидно, що T1(n)+Т2(n)≤с1f(n)+с2g(n). Звідси витікає, що при n≥n0 справедлива нерівність T1(n)+Т2(n)≤(с1+с2)max(f(n),g(n)). Остання нерівність і означає, що T1(n)+Т2(n) має порядок зростання O(max(f(n),g(n))).
Слайд 78 Приклад. Правило сум використовується для обчислення часу послідовного виконання програмних
фрагментів з циклами і галуженнями.
Хай є три фрагменти з
часом виконання відповідно O(n3), O(n2) і О(n log n). Тоді час послідовного виконання перших двох фрагментів має порядок O(max(n2, n3)), тобто О(n3). Час виконання всіх трьох фрагментів має порядок O(max(n3, n log n)), це те ж саме, що О(n3).
У загальному випадку час виконання кінцевої послідовності програмних фрагментів, без урахування констант, має порядок фрагмента з найбільшим часом виконання.
З правила сум також виходить, що якщо g(n)≤f(n) для всіх n, що перевищують n0, то вираз O(f(n)+ g(n)) еквівалентний O(f(n)). Наприклад, О(n2+n) те ж саме, що О(n2).
Слайд 79 Правило добутків. Якщо T1(n) і Т2(n) мають степені зростання O(f(n))
і O(g(n)) відповідно, то добуток T1(n)Т2(n) має ступінь зростання O(f(n)
g(n)).З правила добутків витікає, що O(cf(n)) еквівалентно O(f(n)), якщо с - додатна константа. Наприклад, О(n2/2) еквівалентно О(n2).
Слайд 80 Приклад. Визначення часу виконання програми.
procedure bubble ( var A:
array [1.. n] of integer );
{Процедура впорядковує массив А
в зростаючому порядку } var i, j, temp: integer;
begin
(1) for i:=1 to n-l do
(2) for j:=n downto i+1 do
(3) if A[j-1] > A[j] then
begin {перестановка A[j-1] и A[j] }
(4) temp:= A[j-1] ;
(5) A[j-1]:= A[j];
(6) A[j]:= temp;
end;
end; { bubble }
![Приклад. Визначення часу виконання програми. procedure bubble ( var A: array [1.. n] of integer ); {Процедура](/img/thumbs/db6e42c31b5a0f9266599c6a7ea3f240-800x.jpg "ТЕОРІЯ АЛГОРИТМІВ Приклад. Визначення часу виконання програми. procedure bubble ( var A: array")
Слайд 81 Число елементів n, що підлягають сортуванню, може служити мірою об'єму
вхідних даних.
Спочатку відзначимо, що всі оператори присвоєння мають деякий
постійний час виконання, незалежний від розміру вхідних даних. Таким чином, оператори (4)–(6) мають час виконання порядку О(1). Запис О(1) означає "рівнозначно якійсь константі". Відповідно до правила сум час виконання цієї групи операторів рівний О(max(1,1,1))=О(1). 
Слайд 82 Тепер підрахуємо час виконання умовних і циклічних операторів. Оператори if
і for вкладені один в одного, тому підемо від внутрішніх
операторів до зовнішніх, послідовно визначаючи час виконання умовного оператора і кожної ітерації циклу.Для оператора if перевірка логічного виразу займає час порядку О(1). Ми не знаємо, чи виконуватимуться оператори в тілі умовного оператора (рядки (4)–(6)), але оскільки шукаємо якнайгірший час виконання, то, природно, припускаємо, що вони виконуються. Таким чином, отримуємо, що час виконання групи операторів (3)–(6) має порядок О(1).
Слайд 83 Далі розглянемо групу (2)–(6) операторів внутрішнього циклу. Загальне правило
обчислення часу виконання циклу полягає в підсумовуванні часу виконання кожної
ітерації циклу. Для операторів (2)–(6) час виконання на кожній ітерації має порядок О(1). Цикл виконується n-i разів, тому по правилу добутків загальний час виконання циклу має порядок О((n-i)х1), що дорівнює О(n-i).
Слайд 84 Тепер перейдемо до зовнішнього циклу, який містить всі виконувані оператори
програми. Оператор (1) виконується n-1 раз, тому сумарний час виконання
програми обмежено зверху виразом,який має порядок О(n2).
Таким чином, програма "бульбашки" виконується за час, пропорційний квадрату числа елементів, що підлягають впорядковуванню.
Слайд 85Загальні правила обчислення часу виконання програми
1. Час виконання операторів присвоєння,
читання і запису зазвичай має порядок О(1). Є декілька виключень
з цього правила, наприклад в мові PL/1, де можна присвоювати великі масиви, або в будь-яких інших мовах, що допускають виклики функцій в операторах присвоєння.2. Час виконання послідовності операторів визначається за допомогою правила сум. Тому ступінь зростання часу виконання послідовності операторів без визначення констант пропорційності співпадає з найбільшим часом виконання оператора в даній послідовності.
Слайд 863. Час виконання умовних операторів складається з часу виконання умовно
виконуваних операторів і часу обчислення самого логічного виразу. Час обчислення
логічного виразу зазвичай має порядок О(1). Час для всієї конструкції if-then-else складається з часу обчислення логічного виразу і найбільшого часу, необхідного для виконання операторів, виконуваних при значенні логічного виразу true і при значенні false.
Слайд 874. Час виконання циклу є сумою часу всіх виконуваних ітерацій
циклу, операторів тіла циклу, що у свою чергу складаються з
часу виконання і часу обчислення умови припинення циклу (зазвичай останнє має порядок О(1)). Часто час виконання циклу обчислюється, нехтуючи визначенням констант пропорційності, як добуток кількості виконаних ітерацій циклу на найбільший можливий час виконання операторів тіла циклу. Час виконання кожного циклу, якщо в програмі їх декілька, повинен визначатися окремо.
Слайд 885. Для програм, що містять декілька процедур (серед яких немає
рекурсивних), можна підрахувати загальний час виконання програми шляхом послідовного знаходження
часу виконання процедур, починаючи з тієї, яка не має викликів інших процедур.Якщо є рекурсивні процедури, потрібно з кожною рекурсивною процедурою зв'язати часову функцію Т(n), де n визначає обсяг аргументів процедури; потім отримати рекурентне співвідношення для Т(n), тобто рівняння (або нерівність) для Т(n), де беруть участь значення T(k) для різних значень k.
![Домашнє завдання Прочитати с.181-185 [2] Підготуватися до виконання практичної роботи №1.](/img/thumbs/77fedfd8ab1f4f66748b9bbb20d6e635-800x.jpg "ТЕОРІЯ АЛГОРИТМІВ Домашнє завдання Прочитати с.181-185 [2] Підготуватися до виконання практичної роботи №1.")
