Слайд 1Типы случайных событий и действия над ними.
Теория вероятностей
Слайд 2 Для каждого из
событий определите,
каким оно
является – невозможным,
достоверным или случайным:
а) из 25 учащихся двое справляют день рождения 30 января;
б) из 25 учащихся двое справляют день рождения 30 февраля;
в) из списка 9 класса выбрали одного ученика и это – мальчик;
г) из списка 9 класса выбрали одного ученика и это – девочка;
д) из списка 9 класса выбрали одного ученика и ему – 14 месяцев;
е) из списка 9 класса выбрали одного ученика и ему больше двух лет;
ж) измерили стороны треугольника и сумма двух из них оказалась меньше длины третьей стороны.
Диктант.
|| Противоположное событие (по отношению к рассматриваемому событию А) –
это событие , которое не происходит, если А происходит, и наоборот.
Например, событие А – «выпало четное число очков» и B – «выпало нечетное число очков» при бросании игрального кубика – противоположные.
Придумайте два противоположных события.
Слайд 4Примеры противоположных событий:
если сейчас день, то сейчас не ночь;
если
человек спит, то в данный момент он не читает;
если
число иррациональное, то оно не является четным.
Слайд 5Задание 1
Назовите событие
противоположное данному:
при бросании
монеты выпала решка;
Алеша вытащил выигрышный билет в
розыгрыше лотереи;
в нашем классе все умные и красивые;
мою соседку по парте зовут или Таня, или
Аня;
явка на выборы была от 40% до 47%;
сегодня хорошая погода.
|| Два события А и В называют совместными, если они
могут произойти одновременно, при одном исходе эксперимента, и несовместными, если они не могут произойти одновременно ни при одном исходе эксперимента.
Пример. А – «идет дождь», В – «на небе нет ни облачка» – несовместные.
Пример. Коля и Саша играют в шашки. А – «Коля проиграл», В – «Саша выиграл», С – «Витя наблюдал за игрой» – совместные.
Слайд 7Примеры совместных и несовместных событий:
совместные события:
идет дождь и идет
снег,
человек ест и человек читает,
число целое и четное;
несовместные
события:
день и ночь,
человек читает и человек спит,
число иррациональное и четное.
Слайд 8Задание 2
Укажите совместность
– несовместность случайных
событий:
а) (Катя со Славой играли в шахматы)
А – «Катя выиграла», В – «Слава проиграл»;
б) (Катя со Славой играли в шахматы)
А – «Катя проиграла», В – «Слава проиграл»;
в) (бросили кубик)
А – «выпала шестерка», В – «выпала пятерка»;
г) (бросили кубик)
А – «выпала шестерка», В – «выпало четное число очков»;
д) (взяли кость домино)
А – «одно число 2», В – «сумма обоих чисел 9»;
е) (взяли кость домино)
А – «оба числа больше трех», В – «сумма чисел = 8»;
ж) А – «квадратное уравнение имеет два корня», В – «дискриминант больше нуля»;
з) А – «квадратное уравнение не имеет корней», В – «дискриминант равен нулю».
Слайд 9Действия над событиями
1. Суммой нескольких событий
называется событие, состоящие в
наступлении хотя бы одного из них в
результате испытания.( , )
Если события А и В совместны, то сумма А+В
означает, что наступает событие А, или событие
В, или оба события вместе.
Если события несовместны, то событие А+В
заключается в том, что должны наступить А или
В, тогда + заменяется словом «или». .
Слайд 10Действия над событиями
Пример. В урне находятся
красные, белые и черные шары.
Вынимается один шар. Возможные
события: А – «вынут красный шар», В –
«вынут белый шар», С – « вынут
черный шар».
Тогда А+В означает, что произошло
событие «вынут не черный шар», В+С –
«вынут не красный шар».
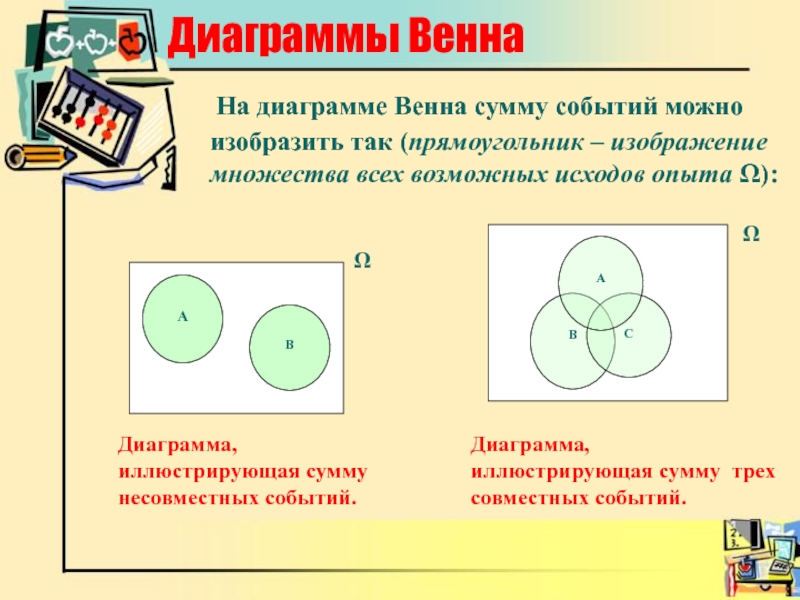
На диаграмме Венна сумму событий можно изобразить так (прямоугольник –
изображение множества всех возможных исходов опыта ):
Диаграмма, иллюстрирующая сумму несовместных событий.
Диаграмма, иллюстрирующая сумму трех совместных событий.
Слайд 12Примеры суммы событий:
пусть А - идет дождь, а В -
идет снег, то (А + В) - либо дождь, либо
снег, либо дождь со снегом, т. е. осадки;
А - пошли на дискотеку; В - пошли в библиотеку, то А + В - пошли либо на дискотеку, либо в библиотеку, т. е. вышли из дома.
Слайд 13Действия над событиями
2. Произведением нескольких событий
называется событие, состоящие в
совместном наступлении всех этих событий в результате испытания.
( ).
Означает союз «и» (АВС, это означает, что
наступило событие А и В и С).
Пример. Пусть имеются следующие события: А – «из колоды карт вынута дама», В – «из колоды карт вынута карта пиковой масти». Значит, А*В означает «вынута дама пик».
Пример. Бросается игральный кубик. Рассмотрим следующие события: А – « число выпавших очков < 5», В – «число выпавших очков > 2», С – «число выпавших очков четное». Тогда А*В*С – «выпало 4 очка».
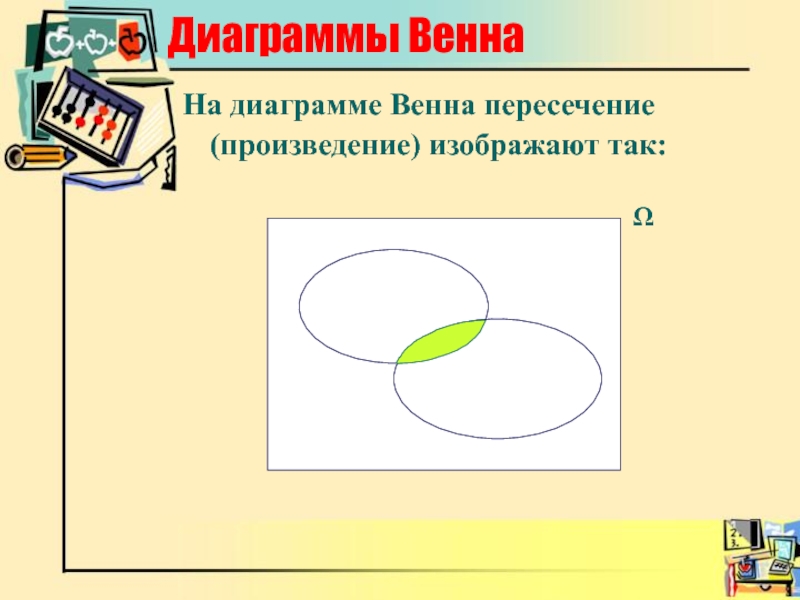
Слайд 14Диаграммы Венна
На диаграмме Венна пересечение
(произведение) изображают так:
Слайд 15Примеры произведения событий:
пусть А - из урны вытянули белый шар,
В - из урны вытянули белый шар, то АВ -
из урны вытянули два белых шара;
А - идет дождь, В - идет снег, то АВ - дождь со снегом;
А - число четное, В - число кратное 3, то АВ - число кратное 6.
Слайд 16Задание 3
Опишите, в
чем состоит сумма
следующих
несовместных
событий.
А – учитель вызвал к доске ученика,
В – учитель вызвал к доске ученицу, А+В – учитель вызвал к доске ученика или ученицу.
Родила царица в ночь:
А – не то сына,
В – не то дочь
А+В – царица родила сына или дочь.
Слайд 17Диаграммы Венна
Графические изображения на плоскости соотношений между множествами
называются диаграммами Венна.
Слайд 18Дополнительные задания
Задание 4. Из событий:
1) «наступило утро»;
2) «сегодня по расписанию шесть уроков»;
3) «сегодня первое января»;
4) «температура воздуха в Салехарде +20С» - составить все возможные пары и выявить среди них пары совместных и пары несовместных событий.
Задание 5. Из полной колоды карт вынимается одна карта. Выяснить, являются совместными или несовместными события:
«вынута карта красной масти» и «вынут валет»;
«вынут король» и «вынут туз».
Слайд 19Вопросы
Могут ли события быть одновременно и несовместными и совместными?
Входит ли
в понятие суммы событий (А + В) событие, состоящее в
одновременном наступлении события А и события В?
Задание.
Укажите события, противоположные данным: а) на кубике выпало 1; б) Света получила на экзамене «5»; в) после ночи наступает утро?