Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
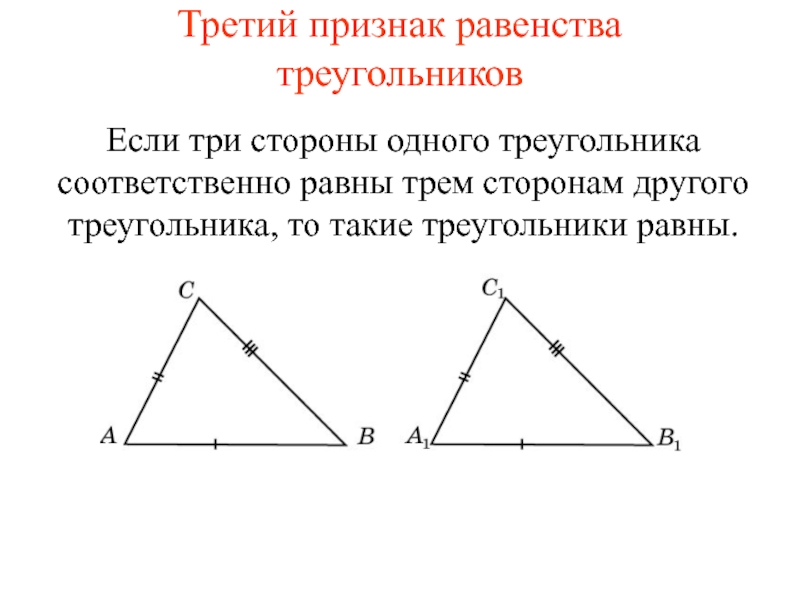
Третий признак равенства треугольников
Содержание
- 1. Третий признак равенства треугольников
- 2. Упражнение 1
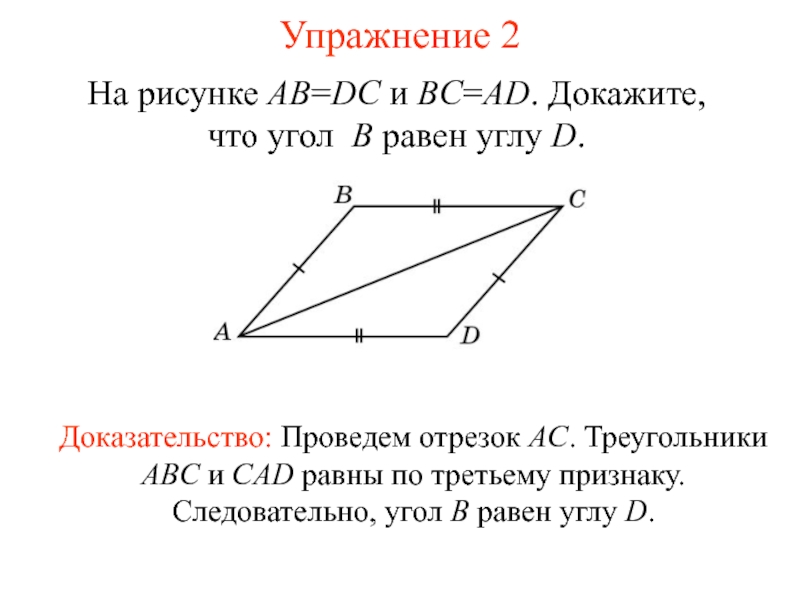
- 3. Упражнение 2На рисунке AB=DC и BC=AD. Докажите, что угол B равен углу D.
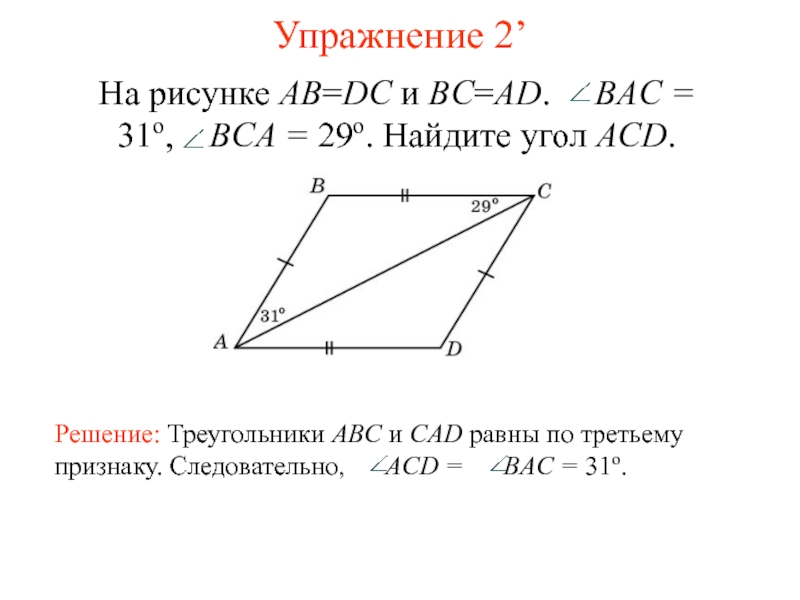
- 4. Упражнение 2’
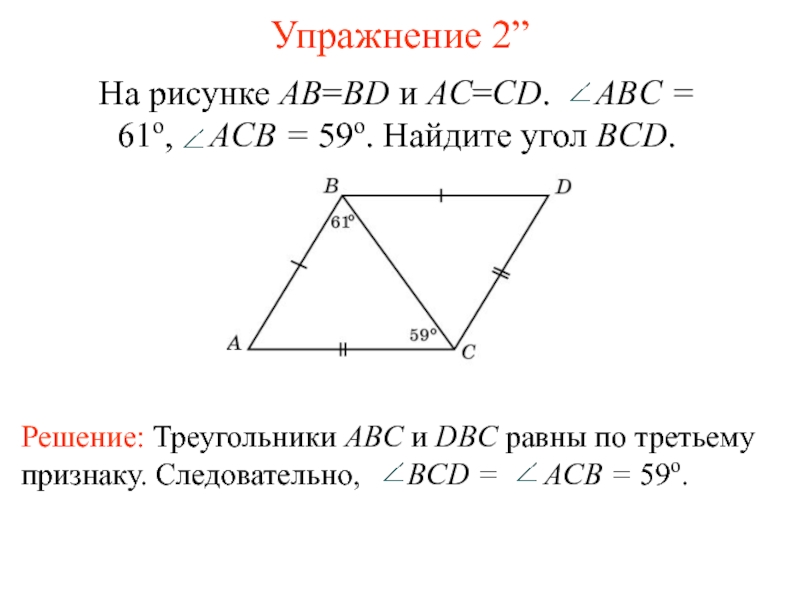
- 5. Упражнение 2”
- 6. Упражнение 3На рисунке АВ = AD и
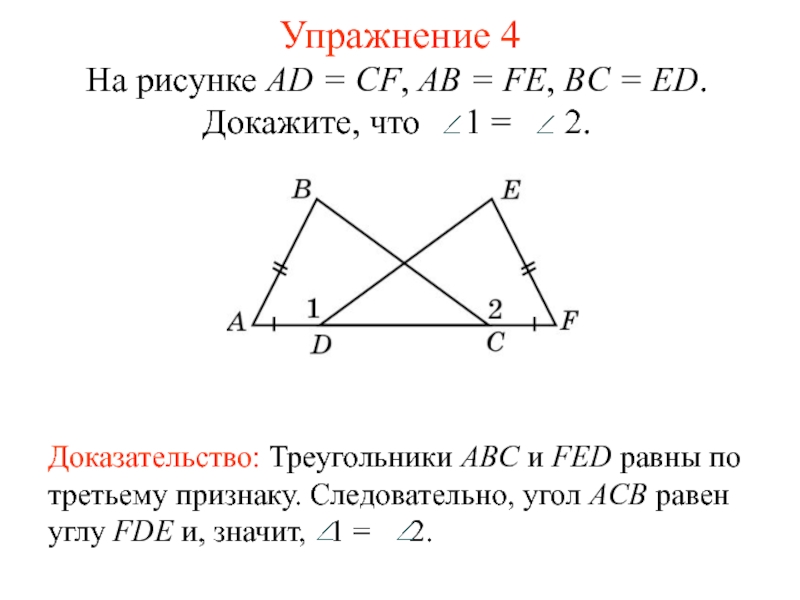
- 7. Упражнение 4
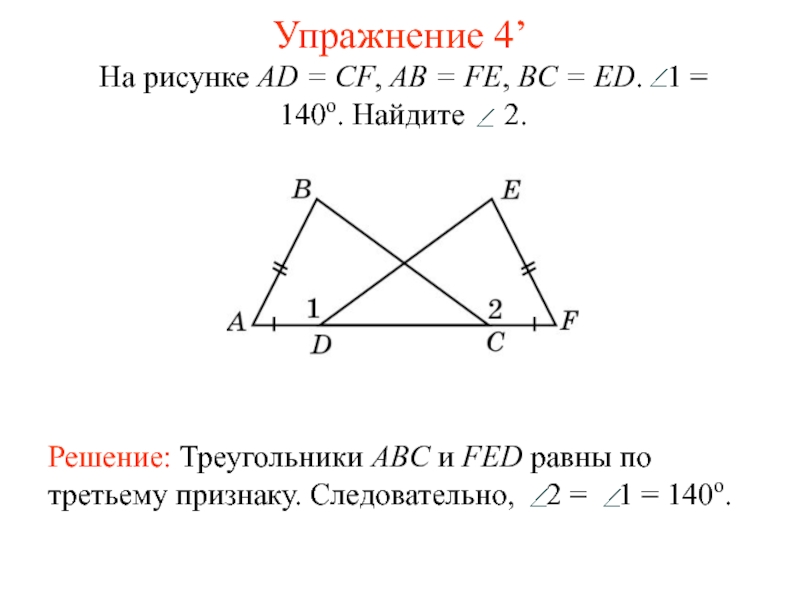
- 8. Упражнение 4’
- 9. Упражнение 5Точки A, B, C, D принадлежат
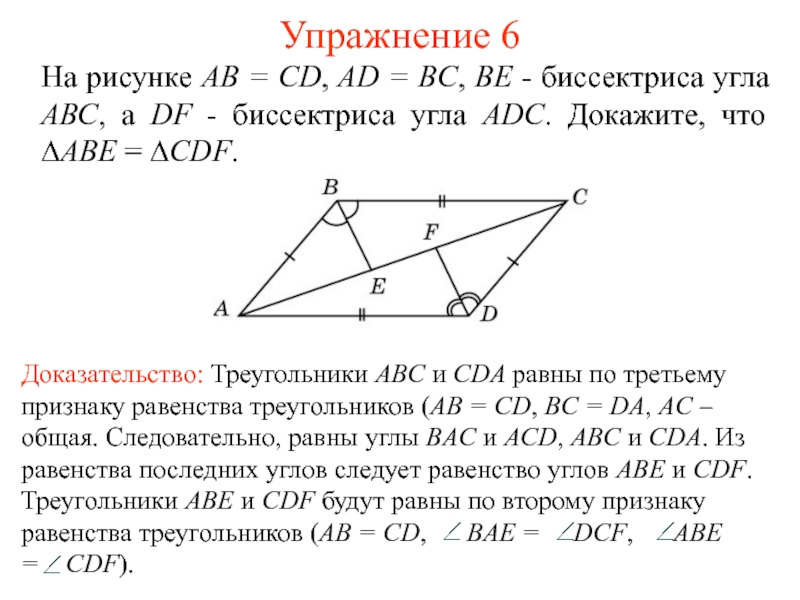
- 10. Упражнение 6На рисунке АВ = CD, AD
- 11. Упражнение 7Докажите, что треугольники ABC и A1B1C1
- 12. Упражнение 8Доказательство: Треугольник OCE равнобедренный (OC =
- 13. Упражнение 9Ответ: а) ADC и BDC; б)
- 14. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Третий признак равенства треугольников
Если три стороны одного треугольника соответственно равны
трем сторонам другого треугольника, то такие треугольники равны.
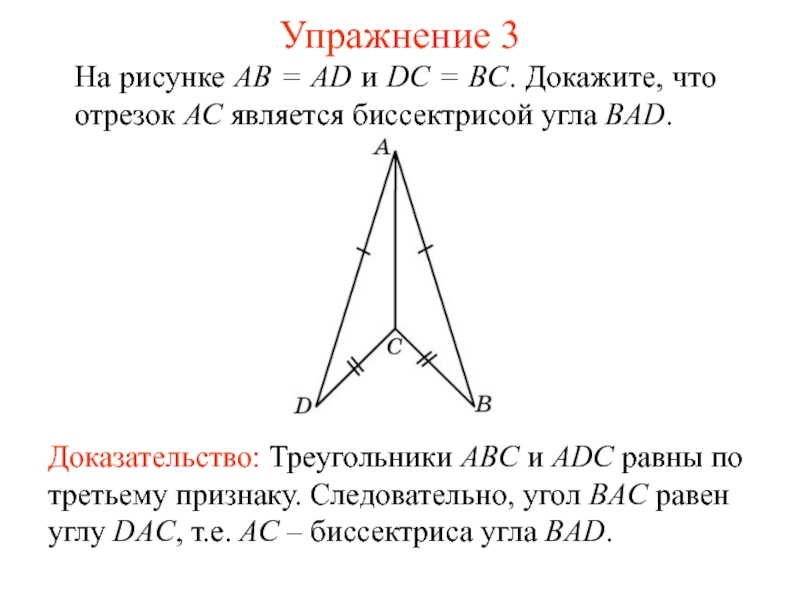
Слайд 6Упражнение 3
На рисунке АВ = AD и DC = BC.
Докажите, что отрезок АС является биссектрисой угла BAD.
Доказательство: Треугольники ABC
и ADC равны по третьему признаку. Следовательно, угол BAC равен углу DAC, т.е. AC – биссектриса угла BAD.Слайд 9Упражнение 5
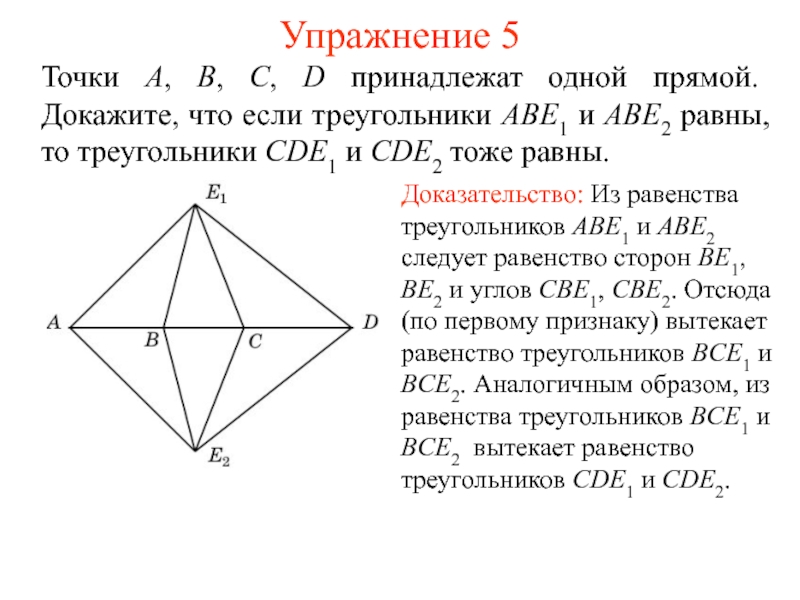
Точки A, B, C, D принадлежат одной прямой. Докажите,
что если треугольники ABE1 и ABE2 равны, то треугольники CDE1
и CDE2 тоже равны.Доказательство: Из равенства треугольников ABE1 и ABE2 следует равенство сторон BE1, BE2 и углов CBE1, CBE2. Отсюда (по первому признаку) вытекает равенство треугольников BCE1 и BCE2. Аналогичным образом, из равенства треугольников BCE1 и BCE2 вытекает равенство треугольников CDE1 и CDE2.
Слайд 10Упражнение 6
На рисунке АВ = CD, AD = BC, ВЕ
- биссектриса угла АВС, а DF - биссектриса угла ADC.
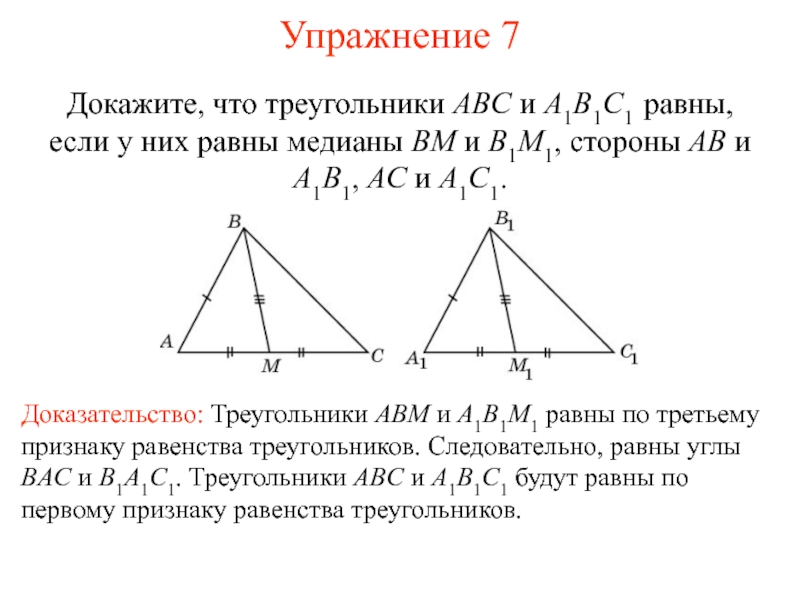
Докажите, что ∆ABE = ∆CDF.Слайд 11Упражнение 7
Докажите, что треугольники ABC и A1B1C1 равны, если у
них равны медианы BM и B1M1, стороны AB и A1B1,
AC и A1C1.Доказательство: Треугольники ABM и A1B1M1 равны по третьему признаку равенства треугольников. Следовательно, равны углы BAC и B1A1C1. Треугольники ABC и A1B1C1 будут равны по первому признаку равенства треугольников.
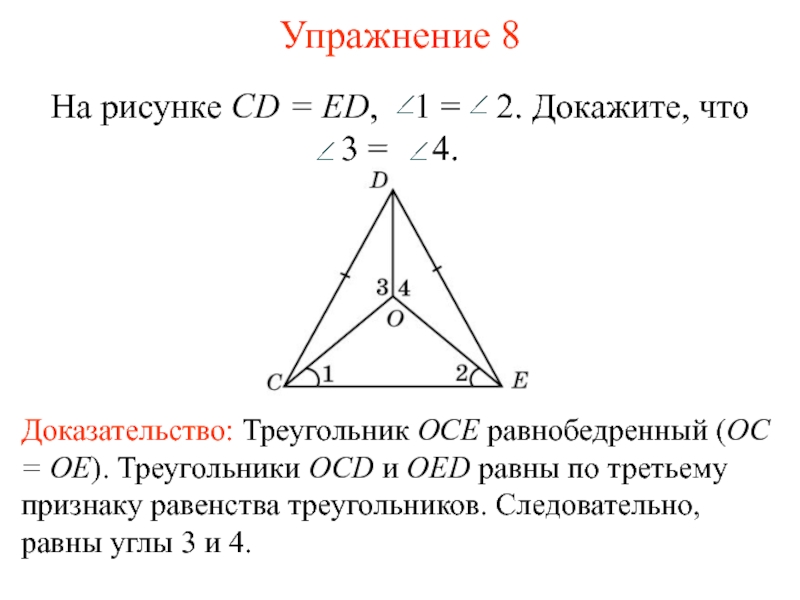
Слайд 12Упражнение 8
Доказательство: Треугольник OCE равнобедренный (OC = OE). Треугольники OCD
и OED равны по третьему признаку равенства треугольников. Следовательно, равны
углы 3 и 4.На рисунке CD = ED, 1 = 2. Докажите, что 3 = 4.
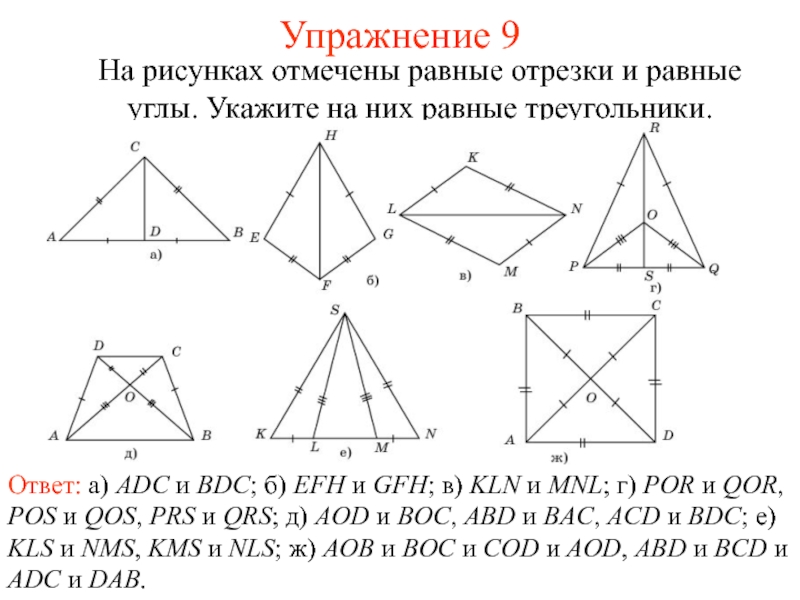
Слайд 13Упражнение 9
Ответ: а) ADC и BDC; б) EFH и GFH;
в) KLN и MNL; г) POR и QOR, POS и
QOS, PRS и QRS; д) AOD и BOC, ABD и BAC, ACD и BDC; е) KLS и NMS, KMS и NLS; ж) AOB и BOC и COD и AOD, ABD и BCD и ADC и DAB.На рисунках отмечены равные отрезки и равные углы. Укажите на них равные треугольники.