Тригонометрические функции

процессов.
Примеры моделируемых явлений.
Вращения:
Астрономические явления
(восход и заход Солнца, изменение фаз Луны,

чередование времён года, морские приливы и отливы)
Опосредованные процессы
(эпидемии гриппа, наполняемость городского транспорта)
Циклы жизнедеятельности человека
(биение сердца, дыхание и др.)
Колебание маятника, пружины, струны.

и с мерой дуги.
Мера должна отражать сам процесс вращения, т.е.

движение точки по окружности в зависимости от времени.
Мера не может зависеть от величины окружности.
Мера должна позволять сравнивать угловые величины с другими объектами математики, оперировать с угловыми величинами.

меры не известны. Градус делили на 60 минут(десятичной системы счисления

ещё не было, число 60 имеет много делителей)
Град (амер.) - 0,01 часть прямого угла.
Румб (морское)-1\32 часть окружности
Деление угломера (артиллерия)-1\6000 часть окружности

радиусу окружности.

Чтобы найти величину угла, который будет служить единицей радианной

меры, надо чтобы

Определение. Угол в 1 радиан – угол, длина дуги которого равна радиусу.

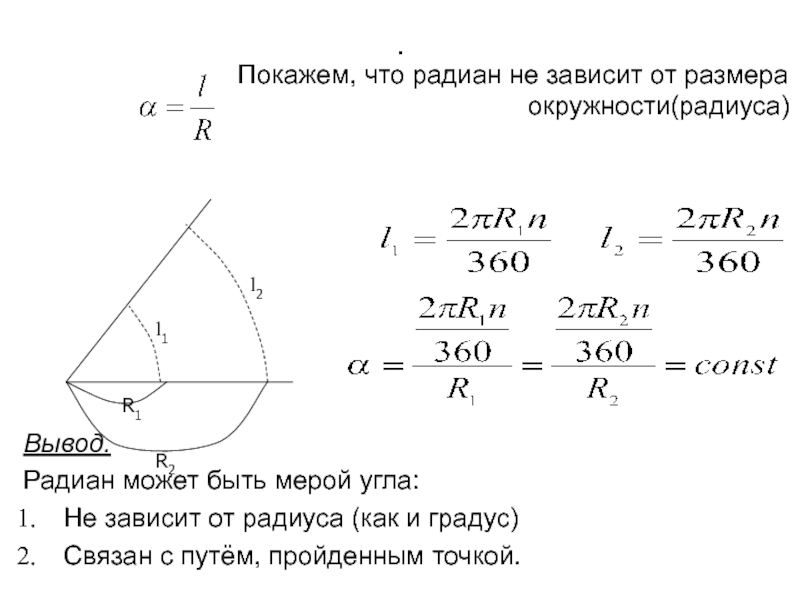
Покажем, что радиан не зависит от

размера окружности(радиуса)








Вывод.
Радиан может быть мерой угла:
Не зависит от радиуса (как и градус)
Связан с путём, пройденным точкой.

R1

R2

l1

l2

величины хорды, дуги и ломаной, звенья которой касаются окружности.




] единица

измерения - радиус окр.



Тогда sinx < x < tgx
Вывод. Выражение дуги или угла в радианной мере позволяет сравнить их с их функциями.

А

C

E

O

R

R

B

D

х

- длина дуги равна радианной мере этой дуги, умноженной на

её радиус.(R=1→ l=α)
обоснование необходимости – удобство, прикладное значение в физике:
Сравните





реальные физич. и мат. задачи потребовали расширения понятия sin(cos) от функции угла к функции числа.(как и в школе)

числа π можно не писать наименование рад» (? →

π=1800 ?)

свойство реальных объектов или явлений:

1) равные объекты имеют равные величины, 2)если объект состоит из конечного числа объектов, то его величина равна сумме величин этих объектов, ….)
Например. Свойство иметь протяженность -…,
иметь вес(притягиваться Землёй) - …,
π - число (π≈22/7≈3,14 … и ещё около 500 тыс. цифр)
Аналог записи «π = 1800». 5 = 5 л = 5 м = 5 г = 5 кг
Вариант записи. π рад = 1800, π – 1800.

углы равны, то равны их sin (cos) .
!!! Смысл теоремы

- теорема единственности. Значение теоремы - sin (cos) углов можно вычислить раз и навсегда.
Теорема позволяет говорить «sin угла 300» и не уточнять, в каком прямоугольном треугольнике.

константы, если к алгебраическим операциям присоединить операцию предельного перехода.
С помощью

степенных рядов




где 0!=1
« - »: слишком абстрактно для введения.
« + »: связь со степенями,
используются в школе, например, у Виленкина для приближенного вычисления значения sinх(cosx) при положительных малых значениях х.
Пример. Вычислить sin 0,12 с точностью до 0,0001.

sin 0,12 = 0,1197 с точн. до 0,0001

(x)+ f '(x)=0, f(0)=0, f '(0)=1
cosx : f '' (x)+

f '(x)=0, f(0)=1, f '(0)=0
« - »: для введения нужна слишком большая теоретическая база.
« + »: доказательство свойств.

проведенная через конец подвижного радиуса

, где ВК –
-

длина отрезка перпендикуляра
от конца подвижного радиуса
до прямой, содержащей неподвижный радиус.

Линия тангенсов - прямая, касающаяся окружности в конце неподвижного радиуса.
« + »: наглядность , частично используется в некоторых методиках

и вектором


« + »: ! наиболее

общий способ,
позволяет брать векторы с началом
в точке, не обязательно лежащей в начале координат,
!! компактное введение, не требует дополнительной теории.
« - »: почти полностью порывает с наглядностью.
Пример. Для углов от 900 до 1800 показать знак и изменение значения функции трудно : проекция должна быть принята за отрицательную.
В школе обычно не рассматривается.

окружности (рис.).
Чтобы окружность стала координатной, надо
выбрать начало отсчёта и

направление движения.
установить соответствие между действительными числами и точками координатной окружности: α→ Pt
а) Действительные числа отображаются на координатную прямую α→t,
b) Точки координатной прямой отображаются на точки координатной окружности единичного радиуса(числовую окружность) t→ Pt. (рис.)

на промежутки вида

[ 2πn; 2π(n+1) ) [ )[ )
Любое действительное число попадёт в какой-либо промежуток.
Вводится отображение f: t → Pt, где tєR, tє [ 2πn; 2π(n+1)), Pt – точка координатной окружности, причём
Устанавливаются свойства этого отображения.(в основной школе на примерах)
Если берём различные числа t ≠ s: t → Pt , s → Ps и Pt = Ps , то t-s= 2πn, nєZ.
Точки, соответствующие противоположным числам, симметричны относительно прямой OP0 ..
Точки вида Pt и Pt+ π диаметрально противоположны.
Если есть такие 4 числа, для которых выполняется |t-s|=|r-q|, то при отображении их на координатную окружность дуги TS=RQ

к координатной окружности.
!!! Каждой точке Р на координатной окружности

соответствуют 2 вида координат: Р → Рt,
Р → (х ; у)
Введение тригонометрических функций числа.
Сравните:
Координата х называется косинусом числа t.
Косинусом действительного числа t называется абсцисса точки, полученной при повороте точки с координатами (1;0) вокруг начала координат на угол х радиан.

любых значений х из области определения функции f(x+Т) = f(x).

Замечания.
0 – период любой функции.
Функция у = f(x) наз. периодической, если она имеет ненулевой период.
f(x+Т) = f(x)= f(x - Т) - теорема: Если Т – период f(x), то (-Т) - период f(x).
Доказательство. f(x - Т)= f(x-Т+Т) = f(x).
Область определения периодической функции должна быть симметрична и бесконечна в обе стороны.
Не все периодические функции –тригонометрические: F(x)=x-[x]={x}
a) D(f)=R b) ]T=1:f(x±1 )= {x±1 } = {x}=f(x)
Определение. Основным периодом функции называется наименьший положительный период Т функции.
!!!Не любая периодическая функция имеет основной период
Пример.у=а, Т=α≠0, α є R или функция Дирихле (док.)
Доказательство. ] Т=r≠0, rєQ.

] xєQ→ (x+r)єQ→ f(x)=f(x+r)=1
] xєR\Q→ (x+r)єR\Q→ f(x)=f(x+r)=-1

Т1 + Т2 – период f(x).
Теорема 2. Если Т0

– основной период f(x), то все остальные периоды ему кратны. Т= nТ0, где nєZ\{0}
Док-во. I . nТ0 – период(следствие Т.1)
II. Других периодов нет(методом от противного)
]Т1>0- период, но Т1≠ nТ0 ,nєN
Тогда Т1≥Т0(т.к. Т0- наим. полож. период)
Значит, сущ. kєN: kT0 0< T1 - kT0 Значит, предположение неверно и не сущ. периода, некратного Т0.
Теорема 3. Если периодические функции С ОБЩЕЙ ОБЛАСТЬЮ ОПРЕДЛЕНИЯ имеют общий период, то и их сумма, разность, произведение , частное и композиция тоже периодические с тем же периодом (док-во Виленкин №505,506)
Теорема 4. Если периодические функции f1 и f2 с общей областью определения имеют соизмеримые периоды, то они имеют общий период.
(соизмеримые Т1 , Т2 : если существует т/n>0: Т1 = т/n ·Т2 или Т1/ Т2= т/n или nТ1=тТ2 =Т – тогда Т – общий период)→для периодических функций выгодно искать не просто общее кратное, а НОК.

областью определения, является основным периодом для суммы функций f1(x),

f2(x), и общим периодом для их произведения, частного, разности и композиции.
Пример1.]f(x): T1=1/3; g(x): T2=2/5. Tобщ.=НОК(1/3; 2/5)=2, 2: 1/3=6; 2: 2/5=5, т.е. 6Тf=5Tg=2
Пример2. h(x): Th= √2; m(x): Tm=2, Th/ Tm =m/n- не рациональное →общего периода нет.

период ?

(т.к. Рх+2π= Рх= Рх-2π – совпадающие точки → имеют одни и те же координаты → cos(x+2π)= cosx= cos(x-2π))
2π – наименьший положительный период ? (м. от пр.)
] сущ. Т>0: для любого х cos(x+Т)= cosx и 0<Т<2π
] х=0 → cos(0+Т)= cos0=1, cosТ=1, Т=2πk
противоречие.
Значит, возможно только то, что 2π- наим. полож. период

Т=2π/а, где а≠0.
y=Atg(ax+b), y=Actg(ax+b) – основным периодом явл. Т=π/а, где

а≠0.
y=f(sin(ax+b)), y=f(cos(ax+b)) – одним из периодов явл. Т=2π/а, где а≠0.
y=f(tg(ax+b)), y=f(ctg(ax+b)) – одним из периодов явл. Т=π/а, где а≠0.

сдвиг графика вдоль ОХ→док-м для y=Asin(ax)
Найдём Т для одного

из х: Asin(a(x+Т))= Asin(ax)
]х=0 → Asin(a(0+Т))= Asin(a0) ; → Asin(aТ)= Asin0 ; |:А → sin(aТ)= 0; aТ= πn,nєZ; Т= πn/a,nєZ
Расположим найденные Т в порядке возрастания Т: π/a, 2 π/a, 3π/a, …
Начиная с наименьшего периода для х=0, доказываем, что он является периодом и для остальных х из ООФ:
]Т= π/a. Док-м Asin(a(x+ π/a))= Asin(ax)? или sin(a(x+ π/a))= sin(ax)?
sin(a(x+ π/a))= sin(ax+ π))= -sin(ax)≠ sin(ax) для любых из D(f) (формулы приведения и нечётность sin)
]Т= 2π/a. Док-м Asin(a(x+ 2π/a))= Asin(ax)?
sin(a(x+ 2π/a))= sin(ax+ 2π))= sin(ax) для любых из D(f)

период(осн. или один из).
y=sin√x
y=sin(2x/5-7)
y=tg(x√2)


y=sin(4x/5+5)+3cos(7x/8)
y=cosx-cos√3x
Ответы.
Нет
Осн., Т=5π
Осн., Т=π/√2
Один из,

Т=3π/√2
Осн.,Т=НОК(5π/2;16 π/7)=80 π
Нет общ.,т.к.периоды несоизмер.

Найдите f(-27), если при хє[0;4] f(x)=2-|x-2|.
f(-x)=f(x) →f(-27)=f(27)
T=8 →f(x+nT)= f(x+8n) →
f(27)=

f(27-8·3)= f(3), где 3є[0;4] →
f(3)= 2-|3-2|=2-1=1.
Ответ. f(-27)=1

уравнения f(х)=2,5, принадлежащие [8;12], если

Решение.
х+2=2,5; х=0,5
2х-1=2,5; х=1,75
т.к. f(х)-чётная, то корнями

будут и х=-0,5;х=-1,75
т.к.Т=4, то корнями будут и хi=х0+пТ= х0+4п→
х=0,5+8=8,5є [8;12]
х=-0,5+12=11,5є [8;12]
х=1,75+8=9,75є [8;12]
х=-1,75+12=10,25є [8;12]
Ответ. 8,5; 9,75; 10,25; 11,5.