Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ЦЕНТРАЛЬНОЕ (ОСЕВОЕ) РАСТЯЖЕНИЕ ИЛИ СЖАТИЕ ПРЯМОГО БРУСА
Содержание
- 1. ЦЕНТРАЛЬНОЕ (ОСЕВОЕ) РАСТЯЖЕНИЕ ИЛИ СЖАТИЕ ПРЯМОГО БРУСА
- 2. ЦЕНТРАЛЬНОЕ (ОСЕВОЕ) РАСТЯЖЕНИЕ ИЛИ СЖАТИЕ.ПРОДОЛЬНЫЕ СИЛЫ
- 3. Определение. Центральным растяжением (сжатием) называют такой вид
- 4. Слайд 4
- 5. Слайд 5
- 6. В общем случае, когда стержень подвергается действию
- 7. ЭПЮРЫ ПРОДОЛЬНЫХ СИЛ. ПРАВИЛА ИХ
- 8. Слайд 8
- 9. Определяем опорные реакции.Для этого составляем уравнение
- 10. б) сечения, где начинают или заканчивают свое
- 11. I участок AВ: 0 ≤ x1
- 12. Составляем выражение для продольной силы
- 13. «Скачки» на эпюре N возможны только в
- 14. 8. Отмечаем опасное сечение стержня, где действует
- 15. Естественно можно предположить, что и внутри
- 16. Слайд 16
- 17. Слайд 17
- 18. Знак напряжения зависит от знака продольной силы
- 19. Для стержня, растягиваемого только двумя силами, приложенными
- 20. σ1 = σ; σ2 = σ3
- 21. ПРОДОЛЬНЫЕ ДЕФОРМАЦИИ Вычисление деформаций и
- 22. (6)Определение. Отношение абсолютного удлинения стержня к его
- 23. ЗАКОН ГУКА ПРИ ЦЕНТРАЛЬНОМ РАСТЯЖЕНИИ ИЛИ СЖАТИИНагрузки
- 24. Слайд 24
- 25. Последней формулой пользуются в случаях, когда какие–либо
- 26. Слайд 26
- 27. Слайд 27
- 28. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ МЕХАНИЧЕСКИХ СВОЙСТВ МАТЕРИАЛОВ И ИХ
- 29. Для определения обобщенных механических характеристик
- 30. На отрезке АВ линейная зависимость нарушается, но
- 31. Определение. Напряжение σпч = σв, соответствующее точке
- 32. Рассмотренные выше напряжения – предел пропорциональности, предел
- 33. Использование реальных диаграмм приводит к большим математическим
- 34. РАСЧЕТ НА ПРОЧНОСТЬ ПРИ ЦЕНТРАЛЬНОМ (ОСЕВОМ) РАСТЯЖЕНИИ
- 35. Механические испытания материалов дают предельные значения напряжений,
- 36. Слайд 36
- 37. (16)В случае пластичного материала за исходное предельное
- 38. –долговечность и значимость сооружения;– уровень развития техники
- 39. Слайд 39
- 40. По известной площади А и допускаемому напряжению
- 41. ПОНЯТИЕ О РАСЧЕТЕ ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ.
- 42. В сопротивлении материалов рассматривается, главным образом, первое
- 43. гдеN1, N2, Nn – нормативные усилия от
- 44. Слайд 44
- 45. Слайд 45
- 46. Слайд 46
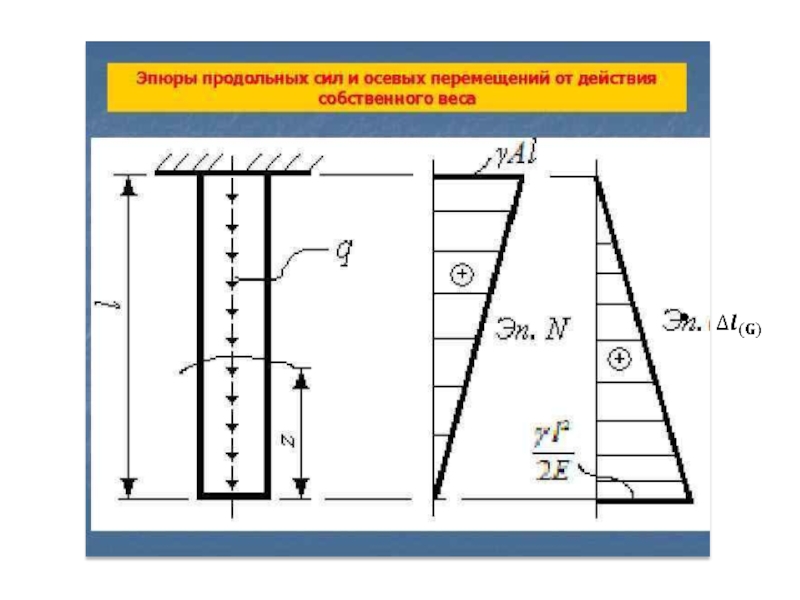
- 47. ЕслиA(x) = A = const,тоq(x) = γ
- 48. Слайд 48
- 49. Слайд 49
- 50. Слайд 50
- 51. Слайд 51
- 52. Слайд 52
- 53. БРУС РАВНОГО СОПРОТИВЛЕНИЯ РАСТЯЖЕНИЮ – СЖАТИЮ.
- 54. В произвольном сечении стержня на расстоянии x
- 55. Интегрируя полученное дифференциальное уравнение с разделенными переменными,
- 56. Имеем (29)Следовательно, ОтсюдаТаким образом (41)
- 57. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ ЗАДАЧИ ПРИ РАСТЯЖЕНИИ ИЛИ
- 58. Определение. Статически неопределимые системы – это упругие
- 59. Оказывается, что всегда можно найти столько дополнительных
- 60. ПОРЯДОК РЕШЕНИЯ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ ЗАДАЧ Статически
- 61. Рассмотрим шарнирностержневую систему, в которой груз F
- 62. Слайд 62
- 63. Согласованность деформаций состоит в том, что до
- 64. Слайд 64
- 65. IV. Синтез уравнений.Решая совместно систему уравнений, полученных
- 66. СПАСИБО ЗА ВНИМАНИЕ!
- 67. Скачать презентанцию
ЦЕНТРАЛЬНОЕ (ОСЕВОЕ) РАСТЯЖЕНИЕ ИЛИ СЖАТИЕ.ПРОДОЛЬНЫЕ СИЛЫ И ИХ ОПРЕДЕЛЕНИЕРассмотрим растяжение бруса внешними силами F, приложенными к его концам. Очевидно, если воспользоваться методом сечений, во всех сечениях возникает продольная сила N,
Слайды и текст этой презентации
Слайд 2
ЦЕНТРАЛЬНОЕ (ОСЕВОЕ) РАСТЯЖЕНИЕ ИЛИ СЖАТИЕ.
ПРОДОЛЬНЫЕ СИЛЫ И ИХ ОПРЕДЕЛЕНИЕ
Рассмотрим растяжение
бруса внешними силами F, приложенными к его концам. Очевидно, если
воспользоваться методом сечений, во всех сечениях возникает продольная сила N, равная внешней нагрузке F. При растяжении продольная сила N направлена от сечения, а при сжатии – к сечению (см. рис.)Слайд 3
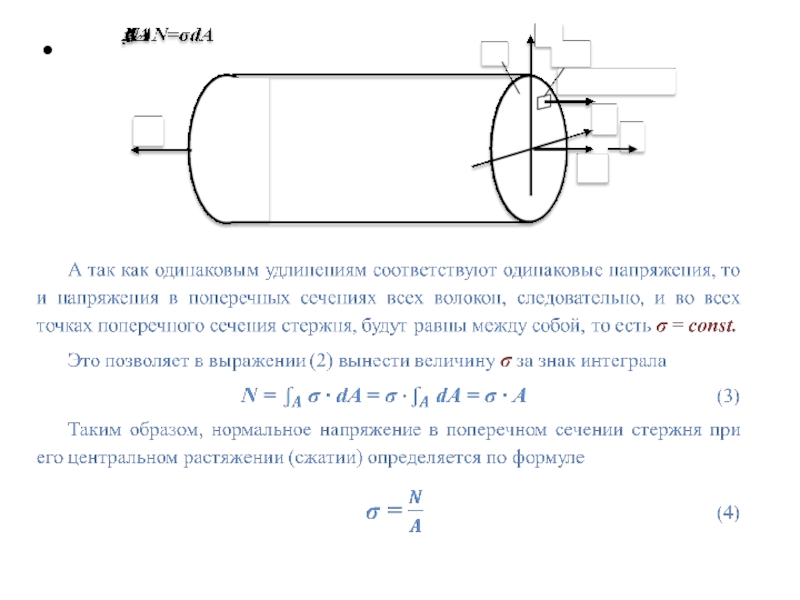
Определение. Центральным растяжением (сжатием) называют такой вид деформации бруса, при
котором в его поперечных сечениях возникают только продольные силы N,
а все прочие внутренние силовые факторы (Q, Мизг и Мк) равны нулю.Как показывают эксперименты, при центральном растяжении или сжатии прямого бруса все его волокна, расположенные вдоль геометрической оси, получают одинаковое удлинение или укорочение.
Определение. Брус, работающий на растяжение или сжатие, называется стержнем.
Определение. Сечения бруса, которые расположены в плоскостях, перпендикулярных к геометрической оси стержня, называются поперечными сечениями.
Слайд 6В общем случае, когда стержень подвергается действию системы внешних сил,
приложенных не только к его торцам, но и в промежуточных
сечениях, значение продольной силы N может быть разным по величине и знаку для различных поперечных сечений.Определение. Продольная сила N в произвольном поперечном сечении стержня численно равна алгебраической сумме проекций на геометрическую ось стержня всех внешних сил, приложенных по одну сторону от рассматриваемого сечения
(1)
Правило знаков. Если продольная сила N вызывает растяжение (удлинение) стержня относительно проведенного сечения, то она считаются положительной (А), а если она вызывает сжатие (укорочение) – отрицательной (Б).
Слайд 7ЭПЮРЫ ПРОДОЛЬНЫХ СИЛ. ПРАВИЛА ИХ ПОСТРОЕНИЯ
Для исследования напряженного
состояния бруса (стержня) необходимо знать, как изменяются продольные силы N
по его длине. Результат исследования закона распределения продольных сил по длине бруса можно представить в виде графика, называемого эпюрой продольных сил.Определение. График, изображающий закон изменения N вдоль геометрической оси стержня, называется эпюрой продольных сил.
Ординаты этой эпюры представляют собой численные значения продольных сил N в соответствующих сечениях стержня.
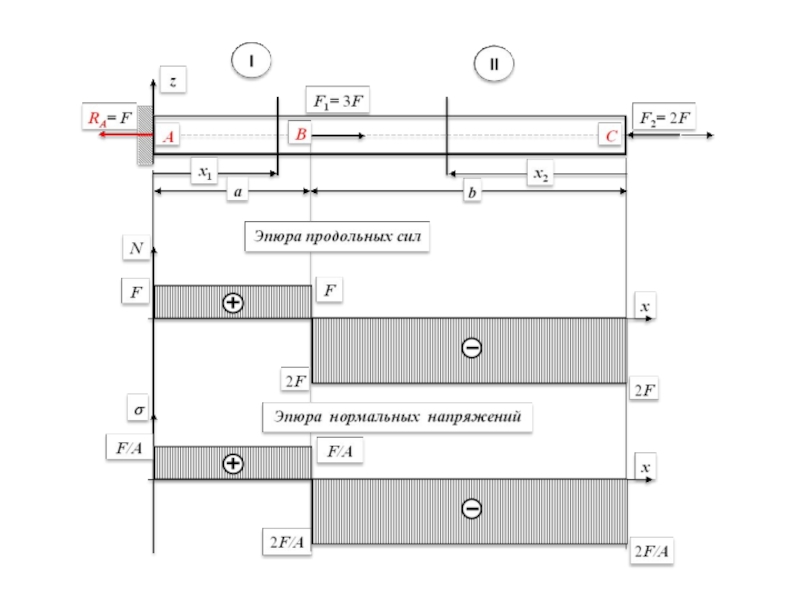
На рисунке изображен стержень постоянного поперечного сечения, жестко защемленный в сечении A и нагруженный внешними силами F1 = 3F и F2 = 2F, направленными вдоль его геометрической оси.
Определим продольные силы, возникающие в его поперечных сечениях, и построим эпюру продольных сил.
Конец стержня защемлен. Очевидно, что опорная реакция RA будет направлена вдоль оси бруса.
Слайд 9 Определяем опорные реакции.
Для этого составляем уравнение равновесия бруса в
виде суммы проекций всех сил на горизонтальную ось x.
Сумма проекций
всех сил на горизонтальную ось x равна нулю: Fx = 0; – F2 + F1 – RА = 0 → RА = F1 – F2 = 3F – 2F = +F.
Следовательно,
RА = +F.
Ниже будет показано, что для консольных стержней (брусьев), в виде исключения, опорную реакцию можно не определять, а вести дальнейший расчет со стороны свободного конца стержня.
Численные значения опорной реакции, в случае необходимости, можно определить по эпюре N, используя правило «скачков».
2. Разбиваем стержень на участки.
Определение. Участком называется часть стержня, в пределах которой закон (уравнение) изменения данного внутреннего усилия (продольной силы) постоянен.
Границами участка являются:
а) сечения, где приложены внешние сосредоточенные силы;
Слайд 10б) сечения, где начинают или заканчивают свое действие внешние распределенные
нагрузки;
в) сечения, где изменяются размеры или форма поперечного сечения;
г) сечения,
где изменяется материал стержня. Таким образом, наш стержень имеет два участка (AB и BC), которые пронумеруем слева направо (см. рис.).
Границами участков, в данном примере, являются сечения, в которых приложены внешние силы.
3. Строим эпюру N по участкам стержня.
Применяя метод сечений, мысленно проводим поперечное сечение в пределах рассматриваемого участка, которое разбивает стержень на две части.
Выбираем ту часть стержня, на которую действует наименьшее число известных нагрузок.
Для определения внутреннего усилия в сечении совершенно безразлично, какую часть стержня рассматривать.
Слайд 11I участок AВ: 0 ≤ x1 ≥ а
(начало отсчета на левом конце стержня).
Определяем величину продольной силы N
на первом участке. Для этого проектируем все внешние силы, расположенные слева от проведенного сечения, на геометрическую ось x бруса. При этом руководствуемся определением внутреннего силового фактора и правилом знаков.Составляем выражение для продольной силы
N (x1) = + RA = + F.
Продольная сила N на первом участке является постоянной, графиком такой функции служит прямая, параллельная оси x. Для построения ее графика определяем значение продольной силы на границах этого участка
N (0) = +F (значение на левой границе участка);
N (a) = + F (значение на правой границе участка).
II участок CВ: 0 ≤ x2 ≥ b (начало отсчета на правом конце стержня).
Определяем величину продольной силы N на втором участке. Для этого проектируем все внешние силы, расположенные справа от проведенного сечения, на геометрическую ось x бруса. При этом руководствуемся определением внутреннего силового фактора и правилом знаков.
Слайд 12Составляем выражение для продольной силы
N (x2) = – F2 = – 2F.
Продольная сила N на втором участке является постоянной, графиком такой функции служит прямая, параллельная оси x. Для построения ее графика определяем значение продольной силы на границах этого участка
N (0) = – 2F (значение на правой границе участка);
N (b) = – 2F (значение на левой границе участка).
По полученным численным значениям продольных сил N в характерных сечениях стержня строим эпюру (график) этого внутреннего усилия, как показано на вышеприведенном рисунке.
Эпюра внутреннего усилия строится на отдельной линии (базисной прямой), параллельной геометрической оси стержня.
На поле эпюры между графиком и базисной прямой ставится знак внутреннего усилия и проводятся ординаты.
4. Делаем проверки правильности построенной эпюры внутреннего силового фактора N.
Слайд 13«Скачки» на эпюре N возможны только в тех сечениях стержня,
где приложены сосредоточенные внешние силы. По величине этот «скачок» равен
этой силе.Таким образом, при построении эпюры N рекомендуется следующий общий порядок действий:
1. Определяем опорные реакции из уравнений равновесия (статики).
2. Разбиваем расчетную схему стержня на участки.
3. Применяя метод сечений, мысленно проводим поперечное сечение в пределах рассматриваемого участка, которое разбивает стержень на две части.
4. Составляем выражение (уравнение), показывающее закон изменения продольной силы N в пределах рассматриваемого участка. При этом руководствуемся определением внутреннего силового фактора и правилом знаков.
5. По этим выражениям вычисляем численные значения продольных сил в характерных сечениях участка (на его границах).
6. По полученным численным значениям продольных сил N строим эпюру (график) этого внутреннего усилия.
7. Делаем проверки правильности построенной эпюры внутреннего силового фактора N.
Слайд 148. Отмечаем опасное сечение стержня, где действует максимальное (наибольшее) по
абсолютной величине значение продольной силы N.
ОПРЕДЕЛЕНИЕ НОРМАЛЬНЫХ НАПРЯЖЕНИЙ
В ПОПЕРЕЧНОМ
СЕЧЕНИИ БРУСАОдна из основных задач сопротивления материалов формулируется следующим образом:
Известны:
- Размеры стержня и внешние продольные силы, приложенные к нему.
Необходимо установить:
- Какие напряжения возникают в поперечных сечениях?
- Как они распределены по сечению?
- Каким образом напряжения зависят от величины нормальной силы и размеров стержня?
При центральном растяжении или сжатии прямого стержня продольные волокна, расположенные на его поверхности вдоль геометрической оси, получают одинаковое удлинение или укорочение.
Слайд 15
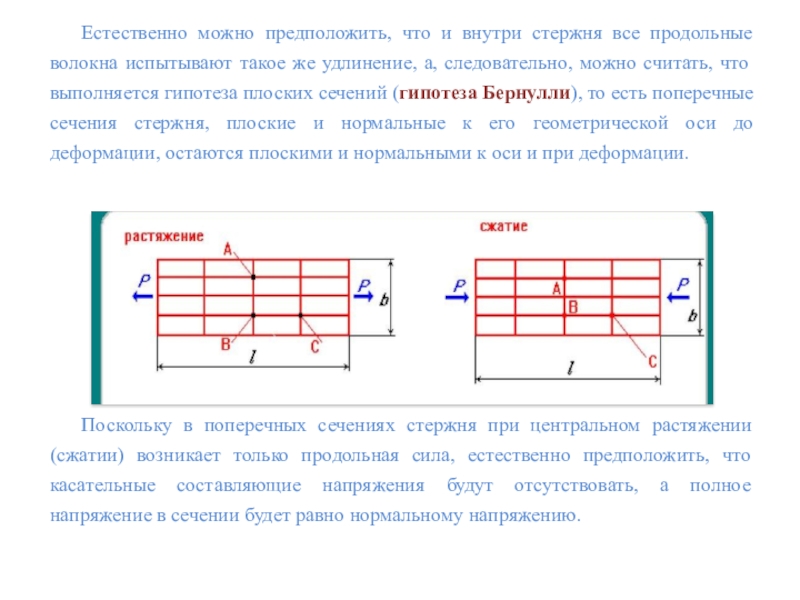
Естественно можно предположить, что и внутри стержня все продольные волокна
испытывают такое же удлинение, а, следовательно, можно считать, что выполняется
гипотеза плоских сечений (гипотеза Бернулли), то есть поперечные сечения стержня, плоские и нормальные к его геометрической оси до деформации, остаются плоскими и нормальными к оси и при деформации.Поскольку в поперечных сечениях стержня при центральном растяжении (сжатии) возникает только продольная сила, естественно предположить, что касательные составляющие напряжения будут отсутствовать, а полное напряжение в сечении будет равно нормальному напряжению.
Слайд 18Знак напряжения зависит от знака продольной силы в рассматриваемом сечении
стержня.
Правило знаков. В случае растяжения нормальные напряжения считаются положительными.
Как
показывает опыт, нормальные напряжения распределены по всему сечению равномерно, если вблизи этого сечения нет точек приложения внешних сил или каких–то геометрических особенностей. Это предположение соответствует принципу Сен-Венана.
Для наглядного изображения изменения нормальных напряжений в поперечных сечениях стержня по его длине строится эпюра нормальных напряжений. Осью (базисной прямой) этой эпюры является отрезок прямой, равный длине стержня и параллельный его оси.
Для стержня постоянного поперечного сечения эпюра σ имеет такой же вид, как и эпюра N, она отличаются от неё лишь принятым масштабом (см. рис.)
Для стержня переменного поперечного сечения вид этих двух эпюр различен. В частности, для ступенчатого стержня эпюра σ имеет «скачки» не только в сечениях, где приложены сосредоточенные осевые силы (здесь имеет «скачки» эпюра N), но и в местах изменения размеров поперечных сечений.
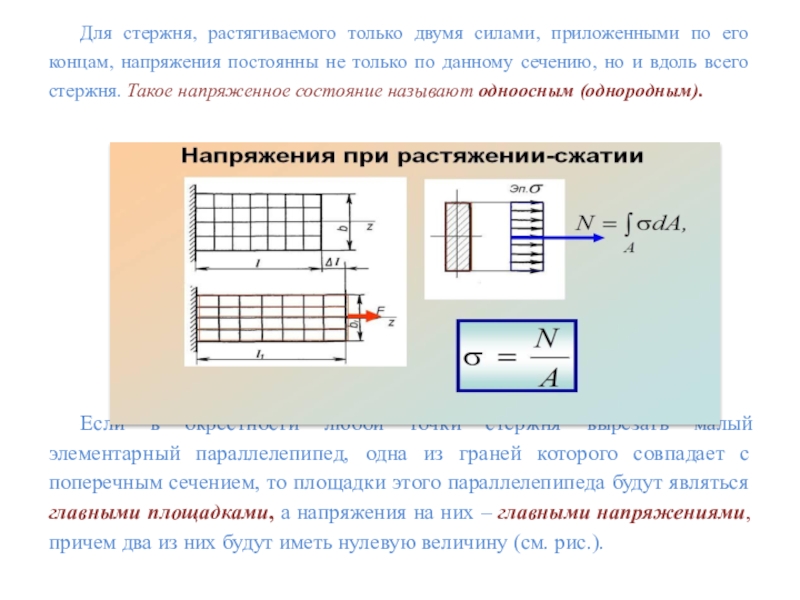
Слайд 19Для стержня, растягиваемого только двумя силами, приложенными по его концам,
напряжения постоянны не только по данному сечению, но и вдоль
всего стержня. Такое напряженное состояние называют одноосным (однородным).Если в окрестности любой точки стержня вырезать малый элементарный параллелепипед, одна из граней которого совпадает с поперечным сечением, то площадки этого параллелепипеда будут являться главными площадками, а напряжения на них – главными напряжениями, причем два из них будут иметь нулевую величину (см. рис.).
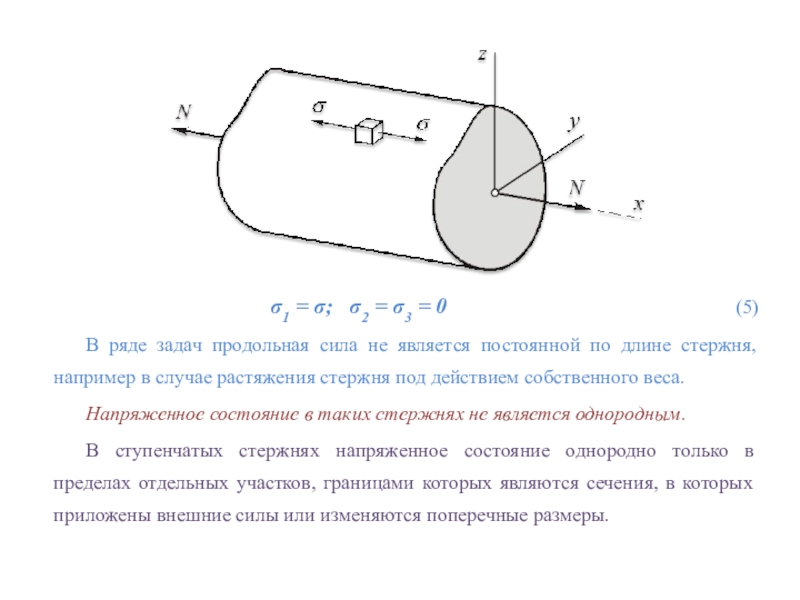
Слайд 20
σ1 = σ; σ2 = σ3 = 0
(5)
В ряде задач продольная сила не является постоянной по длине стержня, например в случае растяжения стержня под действием собственного веса.
Напряженное состояние в таких стержнях не является однородным.
В ступенчатых стержнях напряженное состояние однородно только в пределах отдельных участков, границами которых являются сечения, в которых приложены внешние силы или изменяются поперечные размеры.
Слайд 21
ПРОДОЛЬНЫЕ ДЕФОРМАЦИИ
Вычисление деформаций и перемещений стержня необходимо для его расчета
на жесткость.
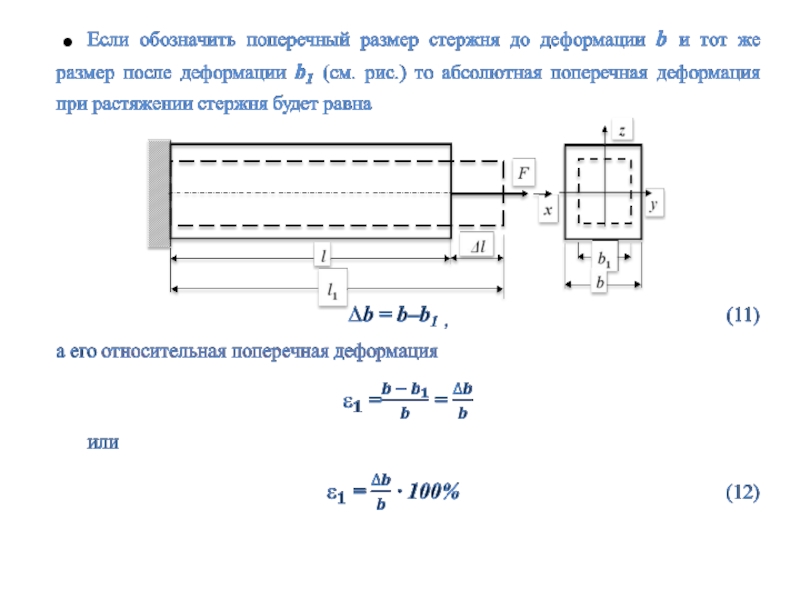
Рассмотрим стержень постоянного поперечного сечения длиной l, заделанный одним
концом и растягиваемый внешней продольной силой F на другом конце (см. рис.).Под действием силы F стержень удлиняется на некоторую величину l и его длина станет равной l + l.
Величина l называется полным или абсолютным удлинением (абсолютной продольной деформацией) стержня.
Абсолютное удлинение, очевидно, зависит от первоначальной длины стержня. Поэтому более удобной мерой деформации стержня является абсолютное удлинение, отнесенное к его первоначальной длине
Слайд 22
(6)
Определение. Отношение абсолютного удлинения стержня к его первоначальной длине называется
относительной продольной деформацией или относительным удлинением ε.
Считается напряженное состояние в
стержне одноосным (однородным), поэтому деформация вдоль оси стержня остается одной и той же, равной своему среднему значению по длине l.Относительное удлинение ε не имеет размерности, это отвлеченное число и часто выражается в процентах от первоначальной длины
∙ 100% (7)
Деформацию удлинения считают положительной, а деформацию сжатия – отрицательной.
Слайд 23ЗАКОН ГУКА ПРИ ЦЕНТРАЛЬНОМ РАСТЯЖЕНИИ ИЛИ СЖАТИИ
Нагрузки и деформации, возникающие
в стержне, тесно связаны между собой. Чем больше величина внешней
силы, растягивающей стержень, тем больше, при прочих равных условиях, его удлинение. Чем больше площадь поперечного сечения бруса, тем удлинение меньше. Опытным путём установлена прямая пропорциональная зависимость между величиной растягивающей силы и соответствующей ей упругой деформацией.Эту зависимость впервые сформулировал английский ученый Роберт Гук.
Определение. При центральном растяжении (сжатии) нормальное напряжение прямо пропорционально относительному удлинению (закон Гука)
σ = Е ∙ ε, (8)
где
Е – коэффициент пропорциональности, называемый модулем упругости первого рода или модулем Юнга.
Слайд 25Последней формулой пользуются в случаях, когда какие–либо из величин N,
E, A непостоянны по длине стержня.
Определение. Произведение E·A (модуля
Юнга на площадь поперечного сечения) называют жесткостью стержня при растяжении.Чем больше жесткость, тем менее податливым является стержень.
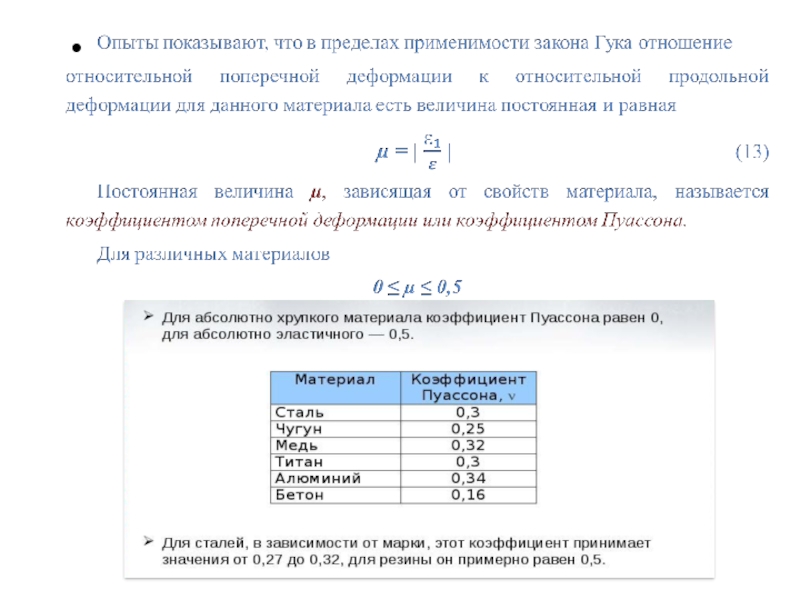
ПОПЕРЕЧНЫЕ ДЕФОРМАЦИИ
Опытом установлено, что даже при весьма малых деформациях стержня в продольном направлении его поперечные размеры изменяются. При растяжении тело удлиняется и становится тоньше, а при сжатии укорачивается и становится толще. Это изменение называется поперечной деформацией стержня.
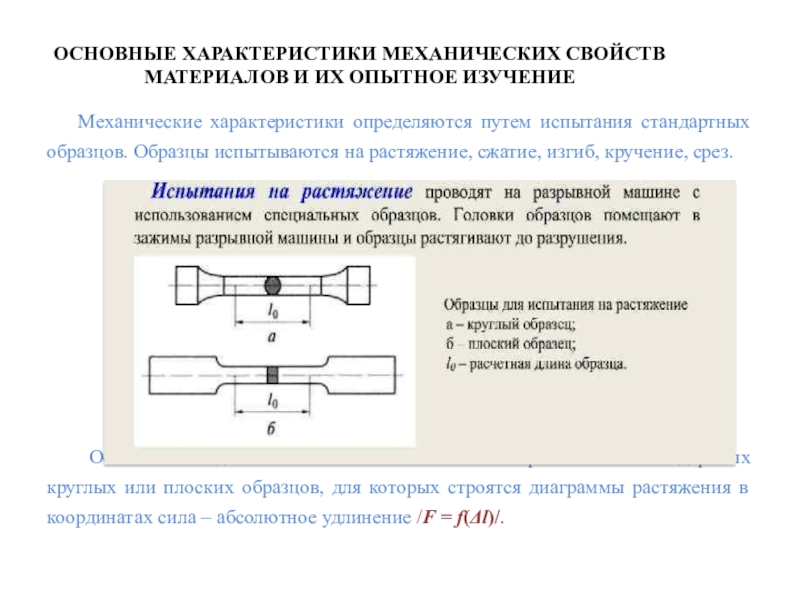
Слайд 28ОСНОВНЫЕ ХАРАКТЕРИСТИКИ МЕХАНИЧЕСКИХ СВОЙСТВ МАТЕРИАЛОВ И ИХ ОПЫТНОЕ ИЗУЧЕНИЕ
Механические характеристики
определяются путем испытания стандартных образцов. Образцы испытываются на растяжение, сжатие,
изгиб, кручение, срез.Основным видом испытаний стали является растяжение стандартных круглых или плоских образцов, для которых строятся диаграммы растяжения в координатах сила – абсолютное удлинение /F = f(l)/.
Слайд 29
Для определения обобщенных механических характеристик материала строят диаграммы напряжения в
координатах напряжение – деформация /σ = f (ε) /.
Рассмотрим
диаграмму напряжения малоуглеродистой стали Ст.3, обладающей высокими пластическими свойствами и широко применяемой в строительстве (см. рис.).На отрезке ОА зависимость между напряжениями и деформациями является линейной.
Определение. Напряжение σпц, соответствующее точке A на диаграмме напряжения, называется пределом пропорциональности.
Слайд 30На отрезке АВ линейная зависимость нарушается, но при разгрузке образца
возникшие деформации исчезают.
Определение. Напряжение σуп, соответствующее точке B на
диаграмме напряжения, называется пределом упругости. Практически горизонтальный отрезок CD называется площадкой текучести.
Определение. Напряжение σт, соответствующее точке D на диаграмме напряжения, называется пределом текучести.
При напряжениях, равных пределу текучести, в малоуглеродистых сталях развиваются пластические деформации, связанные с необратимыми деформациями сдвига между кристаллами феррита.
После развития определенных пластических деформаций и перестройки кристаллической решетки стали несущая способность стержня увеличивается – рост деформаций сопровождается увеличением напряжений, происходит упрочнение стали.
Участок DE на диаграмме напряжения называется зоной упрочнения. При напряжениях, соответствующих наивысшей точке E на диаграмме напряжения, в определенном участке образца появляется значительное уменьшение размеров поперечного сечения – образуется, так называемая, «шейка».
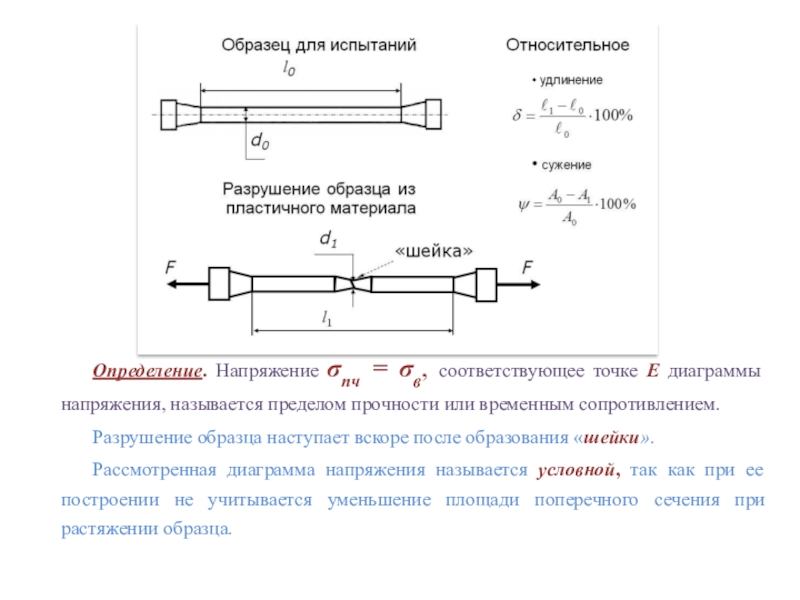
Слайд 31
Определение. Напряжение σпч = σв, соответствующее точке E диаграммы напряжения,
называется пределом прочности или временным сопротивлением.
Разрушение образца наступает вскоре
после образования «шейки».Рассмотренная диаграмма напряжения называется условной, так как при ее построении не учитывается уменьшение площади поперечного сечения при растяжении образца.
Слайд 32Рассмотренные выше напряжения – предел пропорциональности, предел упругости, предел текучести
и предел прочности (временное сопротивление) являются основными механическими характеристиками прочности
и упругости материала.Если довести нагружение образца до точки, лежащей выше предела упругости (точка М), а затем снять нагрузку, то диаграмма разгрузки пойдет по прямой ММ1, параллельной ОА, а отрезок ОМ1 будет соответствовать остаточной деформации. Отрезок М1М2 характеризует упругую деформацию при нагружении образца до точки М. При повторном нагружении образца от точки М1 диаграмма нагружения следует по кривой, практически совпадающей с прямой ММ1. Таким образом, при повторном нагружении как бы повышается предел пропорциональности стали, что связано с изменением микроструктуры в ее кристаллической решетке. При этом площадка текучести исчезает, материал становится более хрупким.
Изменения свойств стали, возникающие при разгрузке и повторном нагружении, называются наклепом.
Участок диаграммы ММ1М называется петлей гистерезиса.
Слайд 33Использование реальных диаграмм приводит к большим математическим трудностям. Существуют различные
способы аппроксимации этих диаграмм с помощью более простых графиков. Так,
например, для стали ВСт. 3, у которой σпц, σуп, σт имеют близкие значения, принимается диаграмма в виде двух прямых, считая, что все три указанных напряжения соответствуют одной точкеТакая диаграмма называется диаграммой Прандтля.
Слайд 34РАСЧЕТ НА ПРОЧНОСТЬ ПРИ ЦЕНТРАЛЬНОМ (ОСЕВОМ) РАСТЯЖЕНИИ ИЛИ СЖАТИИ. МЕТОД
ДОПУСКАЕМЫХ НАПРЯЖЕНИЙ
Основной задачей расчета конструкции является обеспечение её прочности в
условиях эксплуатации.Зная механические характеристики материалов, можно перейти к оценке прочности и соответствующим расчетам при центральном растяжении и сжатии стержней.
Проектирование начинается с выбора материала. При этом учитываются условия работы сооружения, технология изготовления и монтажа конструкций, а также экономические соображения.
Применяемые в строительстве материалы можно условно разделить на пластичные и хрупкие.
Хрупкие материалы разрушаются при очень малых деформациях, а пластичные получают значительные пластические деформации.
Пластичные материалы почти одинаково работают на растяжение и сжатие, а хрупкие, как правило, плохо работают на растяжение и хорошо сопротивляются сжатию.
Слайд 35Механические испытания материалов дают предельные значения напряжений, достижение которых в
элементах конструкций вызывает или разрушение или появление недопустимо больших деформаций.
Для
безопасной работы конструкции необходимо, чтобы максимальные напряжения, возникающие в её элементах, были ниже предельных напряжений (предел прочности, предел текучести).В настоящее время применяются два метода расчета на прочность: по допускаемым напряжениям и по предельным состояниям.
Оба метода преследуют одну цель – обеспечить сооружению прочность и долговечность.
Наиболее распространенным расчетом на прочность при центральном растяжении (сжатии) является расчет по методу допускаемых напряжений, согласно которому наибольшее нормальное напряжение, возникающее в материале, не должно превышать определенной величины, свойственной данному материалу и условиям работы.
Эта величина называется допускаемым напряжением, то есть
σ max ≤ [σ]. (14)
Слайд 37
(16)
В случае пластичного материала за исходное предельное напряжение берется предел
текучести, то есть
(17)
Необходимость введения коэффициента запаса прочности вызывается следующими обстоятельствами:
–
разбросом в определяемых из опытов величинах предела текучести σт и предела прочности σпч для данного материала;– неточностью методов расчета;
– неточностью изготовления деталей;
– отклонением расчетных схем от допущений, принятых при выводе расчетных формул и т.д.
На величину коэффициента запаса прочности влияет ряд факторов:
– качество и степень однородности материала.
Чем однороднее материал, тем меньше можно брать запас прочности
(nст = =1,5 ÷ 3; nбетона = 3; nдерево = 3 ÷ 5 и т.д.);
Слайд 38–долговечность и значимость сооружения;
– уровень развития техники и т.д.
Величины допускаемых
напряжений устанавливаются СНиП (Строительные нормы и правила).
Максимальное нормальное напряжение в
стержне при центральном растяжении (сжатии) возникает в сечении, где продольная сила достигает наибольшей по модулю величины, то есть в опасном сечении.Определение. Сечение, в котором продольная сила принимает максимальное по абсолютной величине значение Nmax, называется опасным сечением стержня по нормальным напряжениям.
Таким образом, наибольшие нормальные напряжения в стержне при центральном растяжении (сжатии) будут равны
(18)
Следовательно, условие прочности при центральном растяжении (сжатии) по нормальным напряжениям по методу допускаемых напряжений имеет вид
Слайд 40По известной площади А и допускаемому напряжению [] определяют наибольшую
величину допускаемой нагрузки
(21)
По найденному значению [N] определяется допускаемое значение внешней
нагрузки.в). Проверочный расчет. По известным значениям N, A, [] проверяют
выполнение условия прочности (19).
Таким образом, виды расчета на прочность при растяжении (сжатии):
Слайд 41 ПОНЯТИЕ О РАСЧЕТЕ ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ. РАСЧЕТ ПО I–Й ГРУППЕ ПРЕДЕЛЬНЫХ
СОСТОЯНИЙ
При помощи одного коэффициента запаса прочности трудно учесть все факторы,
которые для различных сооружений могут проявляться в разных комбинациях. С целью более точного учета влияния различных факторов на величину запаса прочности советские ученые предложили в 1955 году новый метод расчета по предельным состояниям.Определение. Предельным называют такое состояние конструкции, при котором она перестаёт удовлетворять эксплуатационным требованиям.
Нормами установлены три вида предельных состояний:
– Первое предельное состояние, определяемое несущей способностью (прочностью или устойчивостью). На это предельное состояние рассчитываются все конструкции.
– Второе предельное состояние, зависящее от развития чрезмерных деформаций, нарушающих нормальную эксплуатацию конструкции.
– Третье предельное состояние, определяемое образованием или раскрытием трещин (относится, в основном, к железобетонным конструкциям).
Слайд 42В сопротивлении материалов рассматривается, главным образом, первое предельное состояние, связанное
с прочностью конструкции, и отчасти второе.
При расчете по предельным
состояниям запас прочности определяется методом частных коэффициентов.В этом случае коэффициент запаса находится как произведение трех коэффициентов, учитывающих влияние различных факторов: перегрузок (случайные отклонения от нормативных нагрузок), неоднородности материала и условий работы.
Коэффициент перегрузки n учитывает неточности в определении нагрузки. Фактическая нагрузка может отклоняться от нормативной (устанавливается СНиП) в неблагоприятную сторону. Для учета такого отклонения и вводят коэффициент перегрузки, который может быть n > 1, а в отдельных случаях n < 1.
Нормативную нагрузку умножают на этот коэффициент и расчет производят на действие расчетной нагрузки
Nрасч = N1 ∙ n1 + N2 ∙ n2 + ∙∙∙ + Nn ∙ nn, (22)
Слайд 43где
N1, N2, Nn – нормативные усилия от различных видов нагрузки.
n1,
n2, ∙∙∙ nn – соответствующие этим нагрузкам коэффициенты перегрузки.
Полные данные
о величинах коэффициентов перегрузки приведены в СНиП.2. Коэффициент однородности к вводят для учета возможности снижения прочности вследствие неоднородности материала, из которого изготовлена конструкция. Чем однороднее материал, тем ближе к единице коэффициент к.
3. Коэффициент условий работы m учитывает специфические особенности работы материала элементов конструкции и их соединений, например, наличие агрессивной среды, влажности, резких смен температуры и т.д. При неблагоприятных условиях работы принимают m < 1, при нормальных – m = 1, при особо благоприятных условиях работы в отдельных случаях m > 1.
При поставках партий материала, например, стали, бетона, цемента, испытывают образцы, изготовленные из этого материала. Для каждого материала установлено нормативное сопротивление Rн, то есть напряжение, которое как минимум должно быть обеспечено при испытании образцов данной марки.
Слайд 47Если
A(x) = A = const,
то
q(x) = γ ∙ A(x) =
const,
то есть интенсивность распределенной нагрузки изменяется по закону прямой, параллельной
оси стержня.Рассмотрим прямой стержень постоянного поперечного сечения большой длины, закрепленный верхним концом и нагруженный на свободном конце силой F (см. рис.)
Слайд 53
БРУС РАВНОГО СОПРОТИВЛЕНИЯ РАСТЯЖЕНИЮ – СЖАТИЮ.
СТУПЕНЧАТО-ПРИЗМАТИЧЕСКИЕ СТЕРЖНИ (БРУСЬЯ)
При расчете на
прочность стержней постоянного сечения с учетом собственного веса во всех
сечениях, кроме опасного, напряжения будут ниже допускаемого, что приводит к перерасходу материала. Однако, можно спроектировать стержень такого переменного сечения, у которого во всех поперечных сечениях напряжения будут одинаковыми и равными допускаемому напряжению. Такой стержень называется стержнем (брусом) равного сопротивления растяжению или сжатию.Установим закон изменения площади поперечного сечения по длине такого стержня (см. рис.).
Слайд 54В произвольном сечении стержня на расстоянии x выделим бесконечно малый
элемент dx. Определим напряжения в различных сечениях:
Сечение 1 - 1:
Сечение
2 - 2:(37)
Сечение 3 - 3:
где
.
Разделим числитель и знаменатель на Получим
Слайд 55Интегрируя полученное дифференциальное уравнение с разделенными переменными, получим
(38)
Постоянную интегрирования C найдем из условия, что при x = 0 Ax = A0.
Следовательно,
.
. (39)
Если
,
то
(40)
Изготовить брус, имеющий такую сложную форму, затруднительно, поэтому на практике изготавливают брус ступенчато–призматическим таким образом, чтобы в пределах каждого участка верхнее (или нижнее) сечение работало при напряжениях равных .
Слайд 57СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ ЗАДАЧИ
ПРИ РАСТЯЖЕНИИ ИЛИ СЖАТИИ
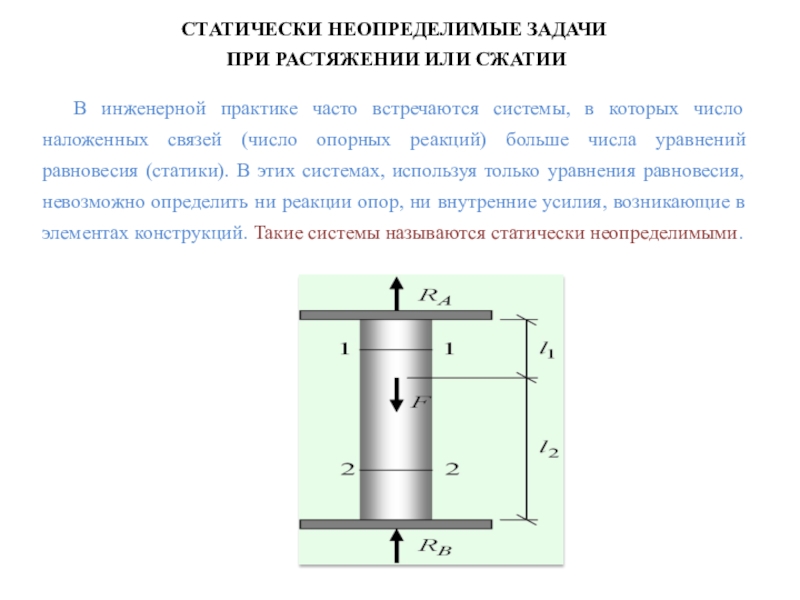
В инженерной практике часто
встречаются системы, в которых число наложенных связей (число опорных реакций)
больше числа уравнений равновесия (статики). В этих системах, используя только уравнения равновесия, невозможно определить ни реакции опор, ни внутренние усилия, возникающие в элементах конструкций. Такие системы называются статически неопределимыми.Слайд 58Определение. Статически неопределимые системы – это упругие стержневые системы, у
которых число неизвестных опорных реакций (внутренних усилий) превышает число независимых
уравнений равновесия (уравнений статики), возможных для этой системы.Определение. Степень статической определимости (неопределимости) простых стержневых систем обычно определяется как разность между количеством неизвестных опорных реакций (внутренних усилий) и количеством уравнений равновесия (уравнений статики), которые можно составить для данной системы.
Для определения всех неизвестных опорных реакций (внутренних усилий) статически неопределимой системы составляют дополнительные уравнения.
Эти необходимые для решения рассматриваемой задачи дополнительные уравнения можно составить, изучая деформации, испытываемые системой.
Всякая конструкция деформируется так, что не происходит разрывов стержней и разъединения их друг от друга. В этом и заключается совместность деформаций элементов системы.
Слайд 59Оказывается, что всегда можно найти столько дополнительных уравнений, сколько необходимо,
чтобы полное число уравнений вместе с уравнениями статики равнялось числу
неизвестных опорных реакций (внутренних усилий).Эти дополнительные уравнения составляются на основании общего принципа – они должны выражать условия совместности деформаций системы, поэтому называются уравнениями совместности деформаций (уравнения перемещений).
Количество дополнительных уравнений совместности деформаций, необходимых для раскрытия статической неопределимости, должно быть равно степени статической неопределимости системы.
Решение системы уравнений равновесия и совместности деформаций позволяет определить все неизвестные опорные реакции (внутренние усилия).
Этот этап решения задачи называется раскрытием статической неопределимости системы.
Раскрыть статическую неопределимость системы - это значит определить численные значения всех опорных реакций (внутренних усилий).
Слайд 60
ПОРЯДОК РЕШЕНИЯ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ ЗАДАЧ
Статически неопределимые конструкции рассчитываются, решая совместно
уравнения, полученные в результате рассмотрения статической, геометрической и физической сторон
задачи. При этом придерживаются следующего порядка:1. Статическая сторона задачи. Определяется степень статической неопределимости системы. Составляются уравнения равновесия, содержащие неизвестные опорные реакции (внутренние усилия) системы.
2. Геометрическая сторона задачи. Рассматриваются деформации, испытываемые системой, и записываются уравнения совместности деформаций (уравнения перемещений).
3. Физическая сторона задачи. На основании закона Гука /Формула (9) для определения перемещений стержня при его центральном растяжении (сжатии), которая получена на основе закона Гука/, уравнения совместности деформаций выражаются через неизвестные опорные реакции (внутренние усилия).
4. Синтез уравнений. Решая совместно систему уравнений, полученных в результате рассмотрения статической, геометрической и физической сторон задачи, определяются численные значения всех опорных реакций (внутренних усилий).
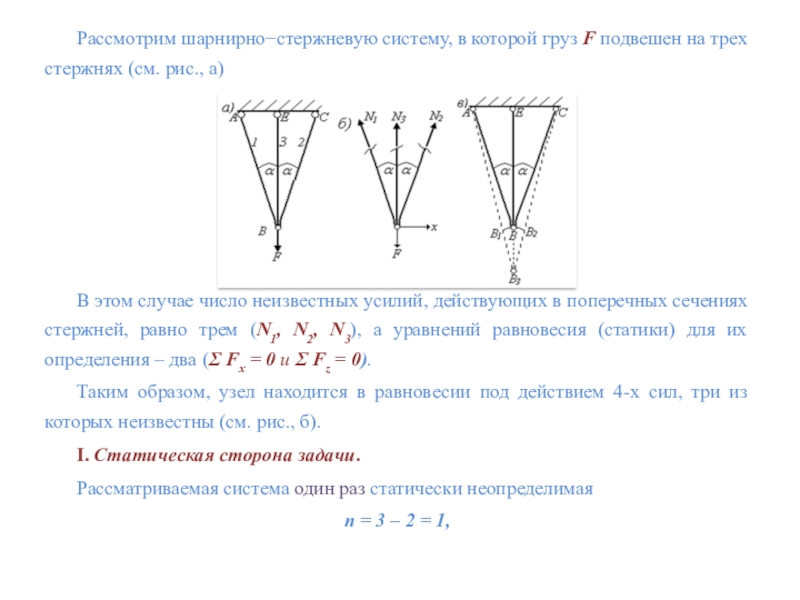
Слайд 61Рассмотрим шарнирностержневую систему, в которой груз F подвешен на трех
стержнях (см. рис., а)
В этом случае число неизвестных усилий, действующих
в поперечных сечениях стержней, равно трем (N1, N2, N3), а уравнений равновесия (статики) для их определения – два ( Fx = 0 и Fz = 0).Таким образом, узел находится в равновесии под действием 4-х сил, три из которых неизвестны (см. рис., б).
I. Статическая сторона задачи.
Рассматриваемая система один раз статически неопределимая
n = 3 – 2 = 1,
Слайд 63Согласованность деформаций состоит в том, что до и после деформации
нижние концы всех стержней должны быть в одном узле. Учитывая,
что деформации стержней малы по сравнению с их линейными размерами, можно считать, что углы, составляемые крайними стержнями со средним, после деформации практически такие же, как и до деформации.Из рисунка (см. рис., в) находим, что отрезок BB3 равен
Для определения удлинения первого стержня, отложим на его новой длине АВ3, первоначальную длину, равную АВ1. В силу малости перемещений дугу ВВ1 заменяем перпендикуляром, опущенным из точки B на линию АВ3. Тогда
= АВ3 – АВ1 = В1В3.
Из прямоугольного треугольника ВВ1В3 установим связь между удлинениями стержней
Следовательно, уравнение совместности деформаций имеет вид
(44)
Слайд 65IV. Синтез уравнений.
Решая совместно систему уравнений, полученных в результате рассмотрения
статической, геометрической и физической сторон задачи, определяются численные значения всех
опорных реакций (внутренних усилий).Мы получили систему трех уравнений (42, 43 и 46), в которые вошли 3 неизвестные N1, N2 и N3.
Решая эту систему уравнений, определим численные значения внутренних усилий N1, N2 и N3.
Из уравнения (43) имеем
(47)
Подставляя в полученное выражение (47) уравнение (46), определим численное значение внутреннего усилия N3
(48)
Подставив в выражение (46) полученное значение N3 (48), определим численные значения внутренних усилий N1 и N2
(49)





























![ЦЕНТРАЛЬНОЕ (ОСЕВОЕ) РАСТЯЖЕНИЕ ИЛИ СЖАТИЕ ПРЯМОГО БРУСА По известной площади А и допускаемому напряжению [] определяют наибольшую величину По известной площади А и допускаемому напряжению [] определяют наибольшую величину допускаемой нагрузки (21)По найденному значению [N] определяется](/img/tmb/7/611290/a9606b5cf5bcb338ce49f8543637d238-800x.jpg)