Слайд 1Цифровые автоматы
Шифраторы и дешифраторы
Слайд 21. Шифратор
Шифратор (кодер) - устройство, осуществляющее преобразование десятичных чисел в
двоичную систему счисления.
Принцип работы:
Пусть в шифраторе имеется m входов, последовательно
пронумерованных десятичными числами (0, 1, 2, 3, ..., m - 1), и n выходов.
Подача сигнала на один из входов приводит к появлению на выходах n- разрядного двоичного числа, соответствующего номеру активного входа.
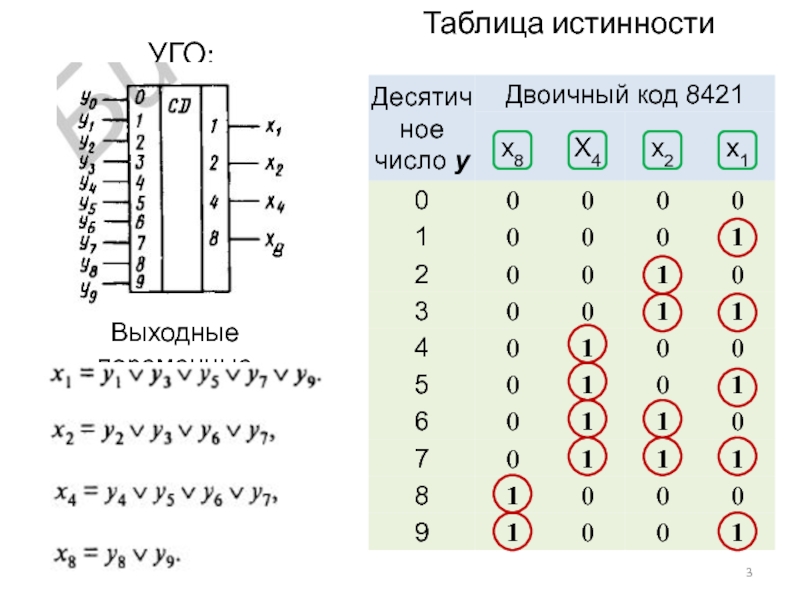
Слайд 3УГО:
Таблица истинности
Выходные переменные
Слайд 4Схема
1
1
1
1
y1 y2 y3 y4 y5 y6 y7 y8 y9
x1
x2
x4
x8
y0
Слайд 52. Дешифратор
Дешифратор (декодер) – устройство, осуществляющее обратное преобразование двоичных чисел
в один управляемый сигнал, снимаемый с выхода.
Принцип работы
Входы дешифратора предназначаются
для подачи двоичных чисел, выходы последовательно нумеруются десятичными числами.
При подаче на входы двоичного числа появляется сигнал на определенном выходе, номер которого соответствует входному числу.
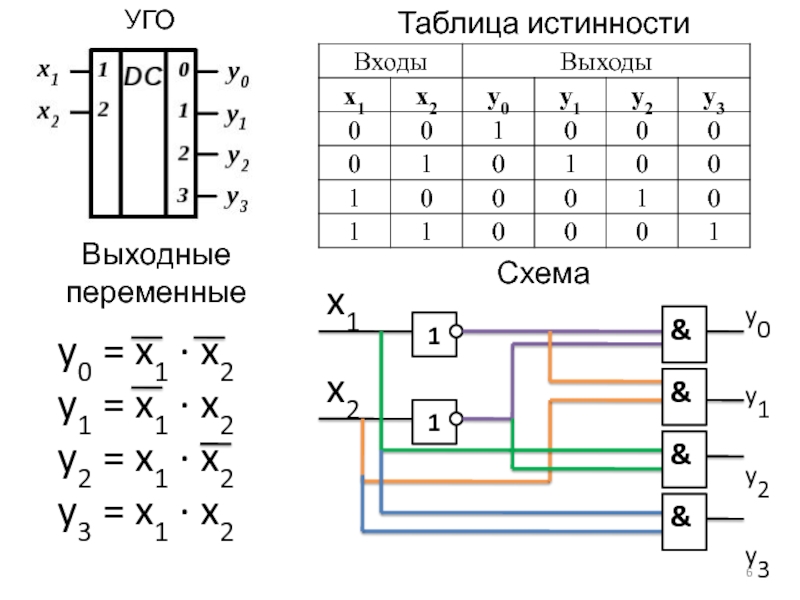
Слайд 6УГО
Таблица истинности
Выходные переменные
y0 = x1 ∙ x2
y1 = x1 ∙
x2
y2 = x1 ∙ x2
y3 = x1 ∙
x2
Схема
x1
x2
&
&
&
&
y0
y1
y2
y3
Слайд 7Дешифратор с 16 выходами для дешифрирования всех возможных комбинаций четырехразрядного
двоичного кода 8421 можно построить из двух дешифраторов с 10
выходами
Слайд 8Реализация произвольной функции алгебры логики на дешифраторах
Функция:
Логические переменные подаются на
адресные входы
дешифратора:
X0 на вход А0,
X1 на вход А0,
X2 на вход A2.
Тогда первый минтерм (110) активизирует выход дешифратора №5,
второй минтерм (101) - выход №3,
третий (0101) – выход №2,
четвертый (100) – выход №4,
пятый (000) – выход №0
1 1 0
1 0 1
0 1 0
1 0 0
0 0 0
Слайд 10Если число минтермов реализуемой функции больше половины числа наборов логических
переменных, то целесообразно реализовать исходную функцию через ее инверсию:
Слайд 11Реализовать на двухвходовых дешифраторах D2_4E функцию F от двух переменных:
Слайд 12Реализовать на двухвходовых дешифраторах D2_4E функцию F от двух переменных:
Слайд 13Реализовать на трехвдоховых дешифраторах функцию y:
Слайд 15Логические уровни элементов
И-НЕ и ИЛИ-НЕ
Таблица истинности для И-НЕ и
ИЛИ-НЕ
Общие сведения
Слайд 16Триггер – устройство, предназначенное для хранения значения одной логической переменной
(или значения одноразрядного двоичного числа)
Активный логический уровень – логический уровень,
наличие которого на одном из входов элемента однозначно определяет логический уровень на его выходе независимо от уровней на других входах.
Q – прямой выход
Q – инверсный выход
Т
Состояние триггера определяется логическими уровнями на выходах Q и Q
Для описания работы триггера используют таблицу состояний (переходов)
Слайд 17Типы входов триггеров
R (англ. Reset) – раздельный вход установки в
состояние 0
S (англ. Set) – раздельный вход установки в состояние
1
К – вход установки универсального триггера в состояние 0
J – вход установки универсального триггера в состояние 1
T – счетный вход
D (англ. Delay) – информационный вход установки триггера в состояние, соответствующее логическому уровню на этом входе
С – управляющий (синхронизирующий) вход
Слайд 18По характеру реакции на входе триггеры делятся на два типа
Синхронные
характеризуется
тем, что входные сигналы действуют на состояние триггера только при
подаче синхронизирующего сигнала на управляющий вход С
Асинхронные
характеризуется тем, что входные сигналы действуют на состояние триггера непосредственно с момента их подачи на входы
Слайд 19Асинхронный RS-триггер
Логическая структура
УГО
Закон функционирования RS-триггера
Таблица состояний
Переключение триггера из одного устойчивого
состояния в другое происходит при подаче активного сигнала на вход.
Триггер
устанавливается в состояние «1», если S = 1.
Если R = 0, остается в состоянии, когда на выходе Q0 = 1
Слайд 20Асинхронный RS-триггер с инверсными входами
Логическая структура
УГО
Для того, чтобы были активными
входные сигналы S и R, на входы подаются инверсии S
и R.
Тогда при S = 1 (или R = 1) полученная S = 0 (или R = 0) и на входе триггера будет действовать уровень лог.0
Активный уровень 0
Слайд 21Синхронные триггеры
Отличие от асинхронного триггера:
синхронизирующий (тактирующий) вход С
Назначение синхронизирующего
входа:
разрешение приема сигналов с информационных входов в заданные временные
интервалы
Слайд 22Синхронные триггеры
Со статическим управлением
С динамическим управлением
Реагируют на изменение сигналов на
информационных входах, происходящие во время действия сигнала на синхронизирующем входе
Прием
сигналов с информационных входов происходит в течение малой длительности фронта сигнала на синхронизирующем входе
Слайд 23Синхронные триггеры со статическим управлением
RS-триггер
Логические структуры
Закон функционирования
Смена логических уровней допускается
тогда, когда С = 0 и триггер не реагирует на
смену логических уровней S и R.
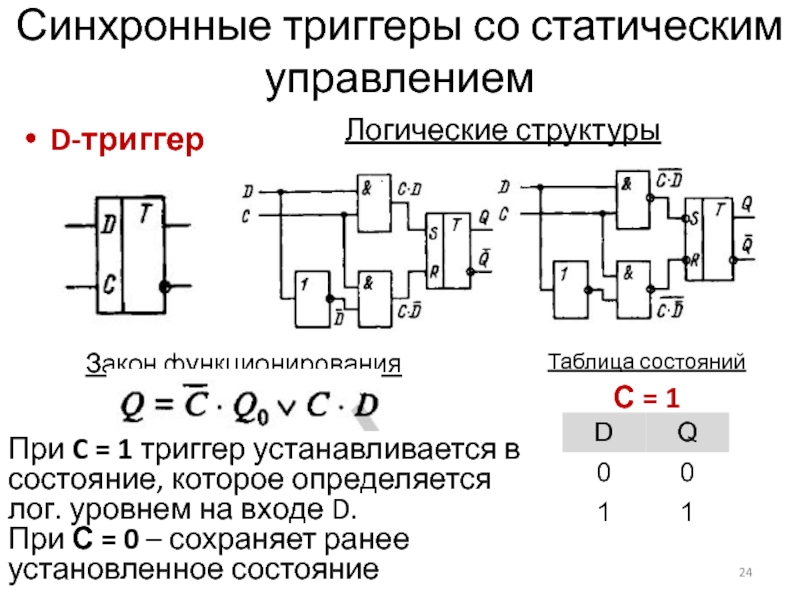
Слайд 24Синхронные триггеры со статическим управлением
D-триггер
Логические структуры
Закон функционирования
Таблица состояний
С = 1
При
C = 1 триггер устанавливается в состояние, которое определяется лог.
уровнем на входе D.
При С = 0 – сохраняет ранее установленное состояние
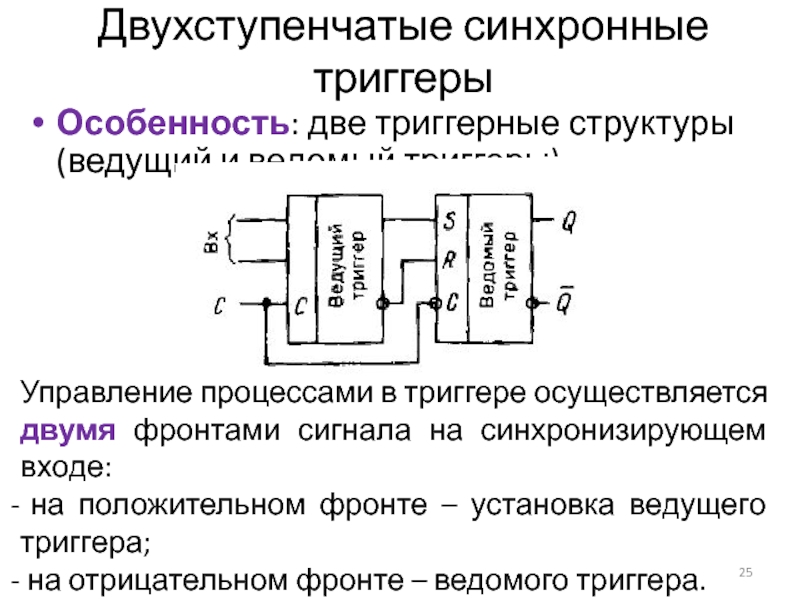
Слайд 25Двухступенчатые синхронные триггеры
Особенность: две триггерные структуры (ведущий и ведомый триггеры)
Управление
процессами в триггере осуществляется двумя фронтами сигнала на синхронизирующем входе:
на положительном фронте – установка ведущего триггера;
на отрицательном фронте – ведомого триггера.
Слайд 26Двухступенчатые синхронные триггеры
JK-триггер
Закон функционирования
Таблица состояний
Состояние Q, в которое устанавливается триггер,
определяется не только логическим уровнем на информационных входах J и
K, но и состоянием Q0, в котором ранее находился триггер.
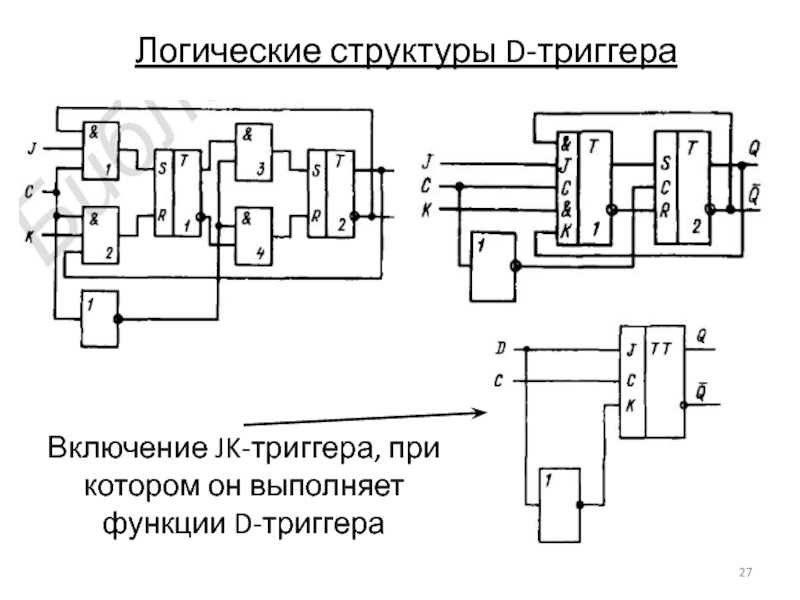
Слайд 27Логические структуры D-триггера
Включение JK-триггера, при котором он выполняет функции D-триггера
Слайд 28Двухступенчатые синхронные триггеры
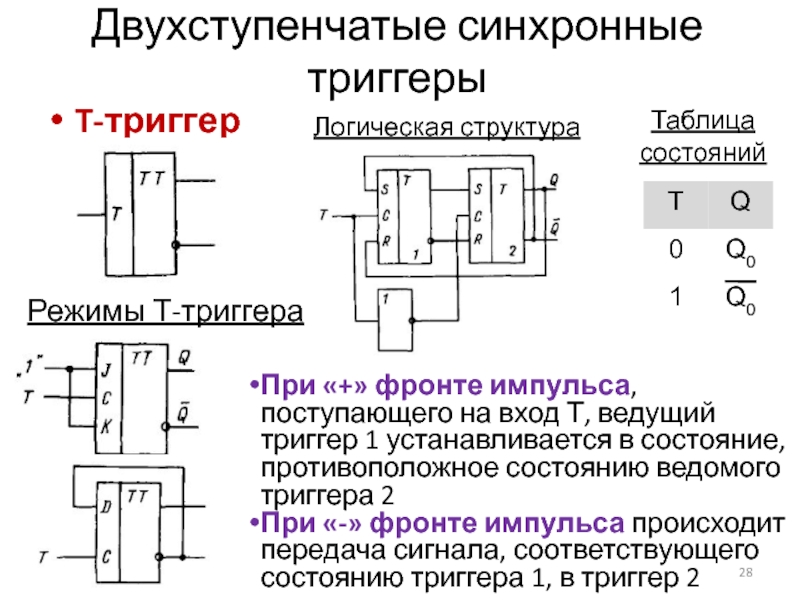
T-триггер
Логическая структура
Режимы Т-триггера
При «+» фронте импульса, поступающего на
вход Т, ведущий триггер 1 устанавливается в состояние, противоположное состоянию
ведомого триггера 2
При «-» фронте импульса происходит передача сигнала, соответствующего состоянию триггера 1, в триггер 2
Таблица состояний
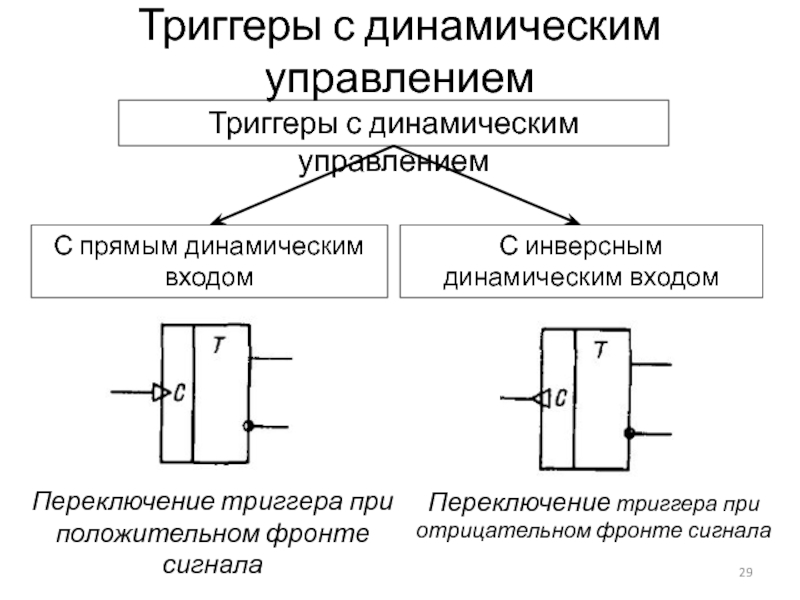
Слайд 29Триггеры с динамическим управлением
Триггеры с динамическим управлением
С прямым динамическим входом
С
инверсным динамическим входом
Переключение триггера при положительном фронте сигнала
Переключение триггера при
отрицательном фронте сигнала
Слайд 30Триггеры с динамическим управлением
D-триггер
JK-триггер
Слайд 31Цифровые автоматы
Мультиплексоры и демультиплексоры
Слайд 32Мультиплексор
Мультиплексор - это устройство, которое обеспечивает подключение к выходу одного
из информационных входов, выбор которого производится кодом, поступающим на управляющий
вход
УГО
Информационные входы
Адресные входы
Стробирующий сигнал
Слайд 33Принцип работы мультиплексора
При отсутствии стробирующего сигнала (C = 0) связь
между информационными входами и выходом отсутствует
При подаче стробирующего сигнала
(C = l) мультиплексор выбирает один из входов, адрес которого задается двоичным кодом на адресных входах, и подключает его к выходу.
nинф = 2nадр
число информационных входов
число адресных входов
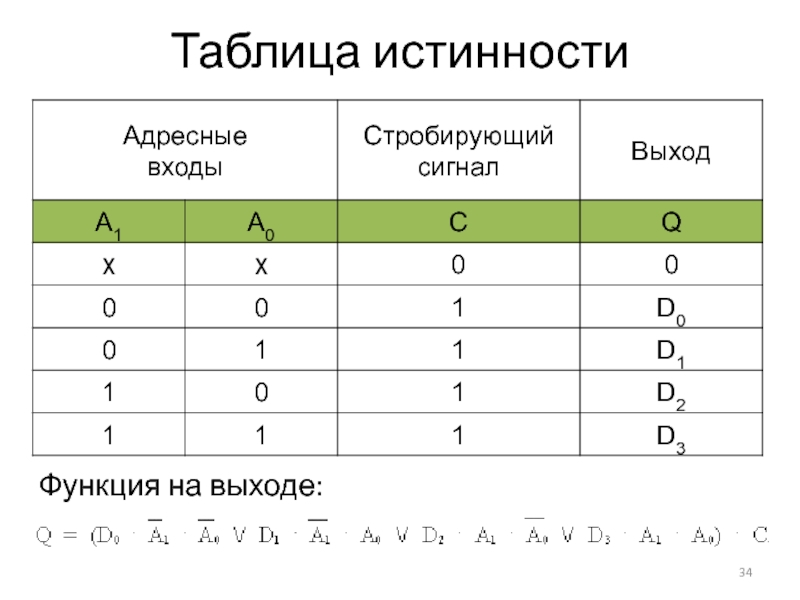
Слайд 34Таблица истинности
Функция на выходе:
Слайд 35Принципиальная схема мультиплексора
Слайд 36Мультиплексорное дерево
Максимальное число входов мультиплексоров - 8
Мультиплексорное дерево -
мультиплексорное устройство с большим числом входов.
Мультиплексоры 1 уровня
Мультиплексор 2 уровня
Слайд 37Схема мультиплексора на базе дешифратора
Слайд 38Демультиплексор
Демультиплексор - это устройство, которое обеспечивает подключение информационного входа к
одному из выходов, выбор которого осуществляется кодом на управляющих входах.
Информационный
вход
Адресные входы
Слайд 39Принцип работы
В соответствии с информацией, заданной на адресных входах, выбирается
выход, к которому подключается информация со входа D
Если D =
1, то демультиплексор превращается в дешифратор
Слайд 40Схемы демультиплексора
Структурная схема
Схема на базе дешифратора
Слайд 41Структура демультиплексора
x1 = 1
x2 = 0
x3 = 0
x4 = 0
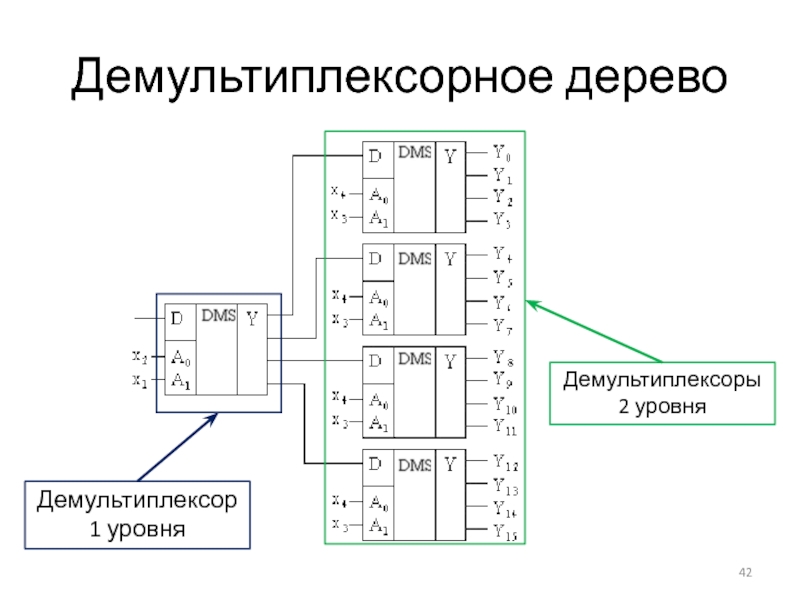
Слайд 42Демультиплексорное дерево
Демультиплексор 1 уровня
Демультиплексоры 2 уровня
Слайд 43Реализация произвольной функции алгебры логики на мультиплексорах
На мультиплексорах, не имеющих
вход стробирования С, можно реализовать любую логическую функцию К+1 входной
переменной
На мультиплексорах, имеющих вход стробирования - логическую функцию К+2 переменных, заменяя при этом несколько корпусов логических элементов малой степени интеграции.
К – число адресных входов мультиплексора.
Слайд 44Указать восьмиразрядное слово Х(X7-X0), которое надо подать на входы мультиплексора
MUX 8-1 для реализации логической функции F(A,B,C) при заданном порядке
подачи переменных A,B,C на адресные входы S2,S1,S0
Слайд 45Указать восьмиразрядное слово Х(X7-X0), которое надо подать на входы мультиплексора
MUX 8-1 для реализации логической функции F(A,B,C) при заданном порядке
подачи переменных A,B,C на адресные входы S2,S1,S0
Слайд 46Реализация произвольной ФАЛ, представленной таблицей истинности, на мультиплексорах
К – определяет
номера информационных входов;
У – логическая функция
Дi – логические величины, поступающие
на i вход
Слайд 47Пусть требуется на мультиплексоре 8:1 реализовать функцию четырех переменных, представленную
в СНДФ:
Слайд 48Цифровые автоматы
Кодопреобразователи
Слайд 49Преобразователи кодов
Преобразователи кодов – логические устройства, с помощью которых код
одного вида преобразуется в код, построенный по другому закону.
Например: двоичный
– в двоично-десятичный
Слайд 50Построение преобразователей кодов
Законы функционирования задаются с помощью соответствующей таблицы
Пример преобразования
кода
Логические уравнения
Слайд 51Построение преобразователей кодов
«Декодер-кодер»:
Входные сигналы подаются на дешифратор
Сигналы с выхода дешифратора
подаются на входы шифратора, число выходов которого равно числу выходов
для кода, в который производится преобразование
Слайд 52«Декодер-кодер»
Таблица соответствия кодов
Слайд 53Программируемые логические матрицы (ПЛМ)
Перемычка
Слайд 54Микросхемы программируемой матричной логики (ПМЛ)
Отличие от ПЛМ:
каждый элемент ИЛИ
постоянно подключен к определенной группе элементов И и не может
произвольно подключаться к выходам любых элементов И.
Достоинство:
сокращение площади программируемой части кристалла;
Снижение стоимости;
Повышение надежности;
Увеличение быстродействия.
Слайд 55Цифровые автоматы
Цифровые компараторы
Слайд 56Цифровые компараторы
Компаратор – логическое устройство, предназначенное для сравнения двух сигналов.
Компаратор
показывает:
равны или не равны два сигнала
если не равны, то какой
из этих сигналов больше
Слайд 57Принцип работы
Связь между сигналами на выходах и входах компаратора при
сравнении двух одноразрядных чисел a и b
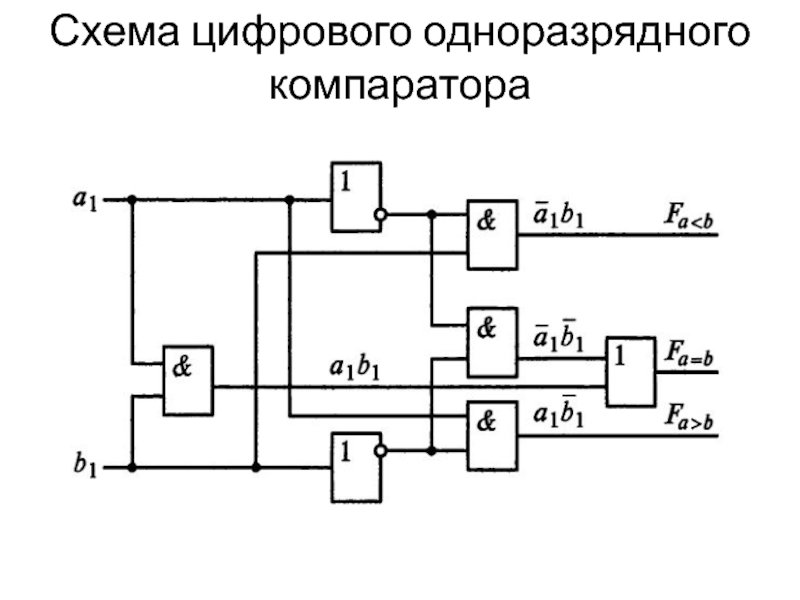
Слайд 58Схема цифрового одноразрядного компаратора
Слайд 59Схема одноразрядного компаратора
Функция Fa=b - «Равнозначность»
Логический элемент «Равнозначность»
Логический элемент «Неравнозначность»
Проверка
равенства разрядов
Слайд 60Поразрядное сравнение
На логических элементах «Равнозначность»
На логических элементах «Неравнозначность»
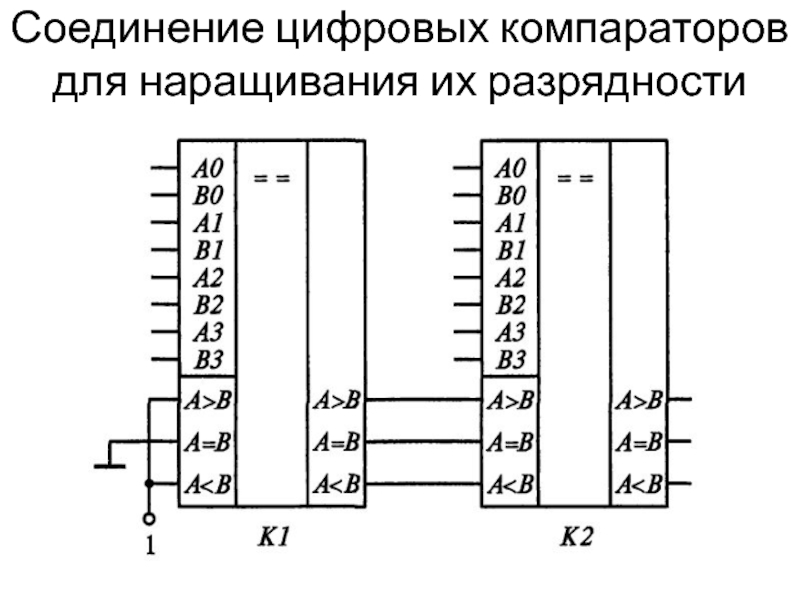
Слайд 61Соединение цифровых компараторов для наращивания их разрядности
Слайд 62Аналоговый компаратор
Схема Графики
Слайд 63Примеры интегральных микросхем компараторов
LM311 (российский аналог — КР554СА3),
LM339 (российский аналог —
К1401СА1)
Схема терморегулятора
Слайд 65Регистры
Основная функция – хранение одного многоразрядного числа.
Регистр для хранения n-разрядного
двоичного числа должен содержать n-триггеров.
Дополнительные функции:
Сдвиг хранимого в регистре числа
на определенное число разрядов влево или вправо
Преобразование числа из последовательной формы в параллельную.
Преобразование из параллельной формы в последовательную
Слайд 66Типы регистров
параллельный
последовательный
Ввод числа осуществляется одновременно всеми разрядами, то есть в
параллельной форме
Ввод числа осуществляется путем последовательной во времени подачей цифр
отдельных разрядов, то есть в последовательной форме
Слайд 67Параллельный регистр
Триггеры устанавливаются в состояния, определяемые поступающими на их входы
цифрами разрядов числа
Регистр на RS-триггерах
Если цифра i-того разряда
аi = 1, то на вход S соответствующего триггера поступает 1 и при подаче уровня лог.1 на вход С триггер устанавливается в состояние 1.
Если аi=0, то 1 поступает на вход R и этот триггер устанавливается в состояние 0
Слайд 680
0
1
0
0
0
0
1
0
0
0
0
0
0
0
0
0
1
0
1
1
0
1
1
Сдвиговый регистр
Временные диаграммы
C
Q4
Q3
Q2
Q1
t
t
t
t
t
Слайд 69Принцип работы:
Выход Q триггера каждого разряда подключен ко входу
D триггера соседнего более младшего разряда.
В момент «+» фронта синхронизирующего
сигнала каждый из триггеров устанавливается в состояние, соответствующее действовавшему на входе D сигналу, и число в регистре оказывается сдвинутым на один разряд
В старший разряд заносится значение, подаваемое извне на вход D триггера этого разряда
Слайд 70Последовательный регистр
Это сдвиговый регистр, в который многоразрядное число вводится последовательно
цифра за цифрой (начиная с цифры младшего разряда) через один
из его крайних разрядов (обычно через старший).
Временные диаграммы
Слайд 72Счетчик – это цифровое устройство, определяющее, сколько раз на его
входе появился некоторый определенный логический уровень.
Числа в счетчике представляются некоторыми
комбинациями состояний триггеров
Принцип работы:
При поступлении на вход очередного уровня лог.1 в счетчике устанавливается новая комбинация состояний триггеров, соответствующая числу, на единицу большему предыдущего числа.
Счетчики
Слайд 73Схема счетчика
Максимальное значение числа, до которого может вестись счет
n -
разрядность счётчика
Слайд 74Таблица истинности двоичного счетчика
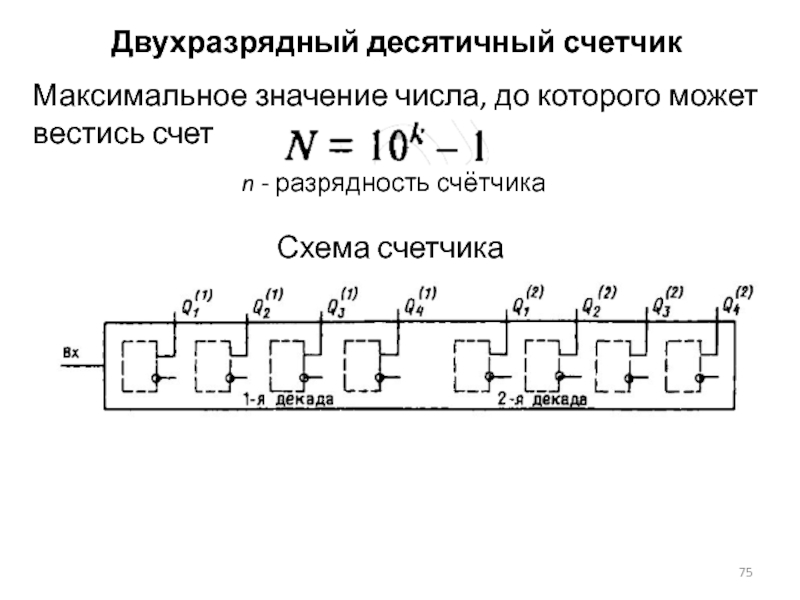
Слайд 75Схема счетчика
Максимальное значение числа, до которого может вестись счет
n -
разрядность счётчика
Двухразрядный десятичный счетчик
Слайд 76Таблица истинности двухразрядного десятичного счетчика
Слайд 77Счетчики
Суммирующие
Вычитающие
В процессе счета каждое очередное число в счетчике на
единицу превышает предыдущее
В процессе счета числа убывают
Реверсивные
Счетчики, которые допускают в
процессе работы автоматическое переключение из режима суммирующего счетчика в режим вычитающего счетчика и наоборот
Слайд 78Суммирующий двоичный счетчик
Поступление на вход лог.1 вызывает увеличение на единицу
хранимого в счетчике числа.
Особенности
Если цифра некоторого разряда остается неизменной, либо
изменяется с 0 на 1, то при этом цифры более старших разрядов не изменятся
Если цифра некоторого разряда изменяется с 1 на 0, то происходит инвертирование следующего за ним более старшего разряда
Слайд 79Временные диаграммы
Принцип работы:
Если на счетном входе С триггера действует импульс,
то его положительным фронтом переключается ведущая часть триггера, на отрицательном
– ведомая.
При каждом изменении сигнала на счетном входе с лог. 1 на лог. 0 изменяется на противоположное состояние выхода триггера. Таким образом, на отрицательном фронте сигнала на выходе триггера происходит переключение следующего за ним триггера более старшего разряда.
Слайд 80Вычитающий счетчик
Поступление на вход лог.1 вызывает уменьшение хранившегося в счетчике
числа на единицу
Если в младшем разряде содержится «0», то он
сопровождается возникновением переносов до тех пор, пока не обнаружит «1».
Правило вычитания
Слайд 81Вычитающий счетчик
Таблица функционирования
Слайд 82Реверсивный счетчик
Две цепи переносов:
1 – соответствует схеме суммирующего счетчика
2 –
соответствует схеме вычитающего счетчика
Слайд 83Десятичный счетчик
Десятичные счетчики применяются, когда число поступающих импульсов нужно
представить в десятичной системе счисления
Слайд 84Основные параметры счетчиков
Модуль счета, или коэффициент пересчета N
Быстродействие счетчика;
fсч –
частота счетных импульсов;
tу сч – время установки счетчика.
Слайд 85Пример: Асинхронный суммирующий двоичный трехразрядный счетчик
Временные диаграммы
Для построения вычитающего счетчика
нужно соединить последовательно не прямые, а инверсные выходы триггеров.
Слайд 86Таблица переходов суммирующего двоичного трехразрядного счетчика
Слайд 87Пример: Десятичный счетчик импульсов
Таблица переходов
Слайд 88Делитель частоты – устройство, которое при подаче на его вход
периодической последовательности импульсов формирует на выходе такую же последовательность, но
имеющую частоту повторения импульсов, в некоторое число раз меньшую, чем частота импульсов входной последовательности.
Отличие от счетчиков:
в делителе частоты последовательность состояний может быть выбрана произвольной, важно лишь обеспечить заданный период цикла N
Делители частоты импульсной последовательности
Слайд 89Делитель частоты с коэффициентом деления N = 2
Схема
Временная диаграмма
Слайд 90Делитель частоты с коэффициентом деления N = 2n
Схема (N=5)
На выходе
каждого делителя частота следования импульсов вдвое ниже, чем на входе
Слайд 91Временная диаграмма
На выходах триггеров всегда образуется последовательность импульсов с частотой
в 5 раз большее низкой, чем частота на входе делителя.
Делитель
частоты с коэффициентом деления N = 5
Слайд 92Делитель частоты с коэффициентом деления N = 5
Таблица состояний
Слайд 93Делитель частоты с коэффициентом деления N = 3
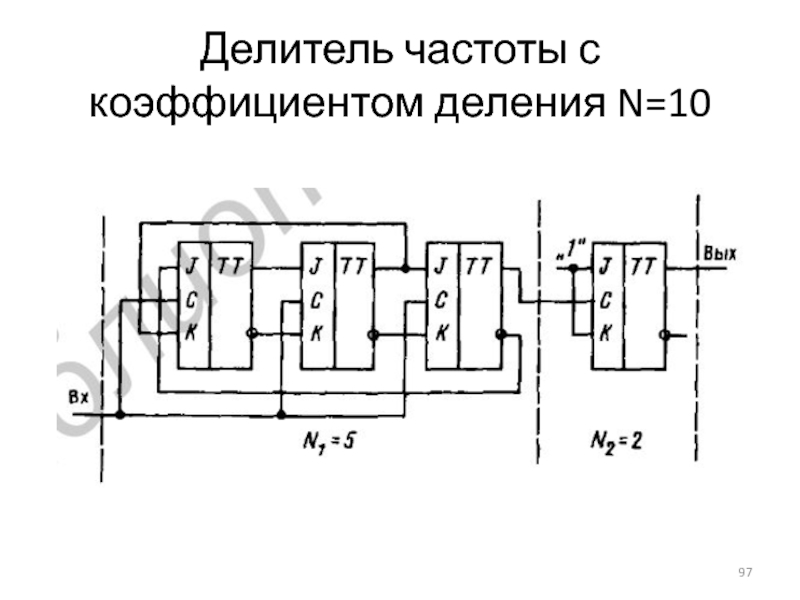
Слайд 94Каскадные делители частоты
В тех случаях, когда коэффициент деления N не
является простым числом и может быть представлен произведением вида :
N = Nl . N2 . N3 . ... . Nk,
схема делителя строится в виде каскадного соединения делителей, имеющих коэффициенты деления N1, N2, N3, ... , Nk
Слайд 95Делитель частоты с коэффициентом деления N=6
Слайд 96Делитель частоты с коэффициентом деления N=9
Слайд 97Делитель частоты с коэффициентом деления N=10
Слайд 98Задания для самостоятельного решения
Построить счетчик со значением периода:
N=7
N=9
N=21
Построить делитель частоты
с коэффициентом деления
N=14
N=15
N=18
Слайд 100Сумматор - это логический операционный узел, выполняющий арифметическое сложение кодов
двух чисел.
Классификация
1. По системе кодирования:
-Двоичные
-Двоично-десятичные
-Десятичные
2. По количеству одновременно обрабатываемых
разрядов складываемых чисел:
-Одноразрядные
-Многоразрядные
3. По числу входов и выходов:
-Четвертьсумматоры
-Полусумматоры
-Полные одноразрядные двоичные сумматоры
Сумматоры
Слайд 101Классификация
4. По способу выполнения операций:
-Последовательные
-Параллельные
-Параллельно-последовательные
5. По способу организации суммирования:
-Комбинационные
-Накапливающие
Параметры сумматоров
Разрядность
Статические
параметры (UВХ, IВХ)
Динамические параметры
Слайд 102Четвертьсумматор
Названия схемы:
Элемент «сумма по модулю 2»
Элемент «исключающее ИЛИ»
УГО
Эквивалентный элемент
Таблица истинности
Уравнение
Слайд 105Четвертьсумматор
3) С использованием только одного инвертора
Слайд 106Полусумматор
Принцип действия:
Определяется цифра суммы путем сложения по модулю 2 цифр
слагаемых и поступающего в данный разряд переноса и формируется перенос,
передаваемый в следующий разряд.
УГО
Сумма
Перенос
Цифры разрядов слагаемых
Слайд 107Полусумматор
Таблица истинности
Уравнения
Схема
Слайд 108Полный одноразрядный двоичный сумматор
Используется для сложения более двух двоичных цифр.
УГО
Сумма
Перенос
в старший разряд
Слагаемые
Перенос из предыдущего (младшего) разряда
Слайд 109Полный одноразрядный двоичный сумматор
Таблица истинности
Уравнения
Уравнение для переноса может быть минимизировано:
Слайд 110Полный одноразрядный двоичный сумматор
Схема полного двоичного сумматора, реализованная на двух
полусумматорах
Слайд 111Полный одноразрядный двоичный сумматор
Пример сложения двух двоичных чисел:
1011 и
1110
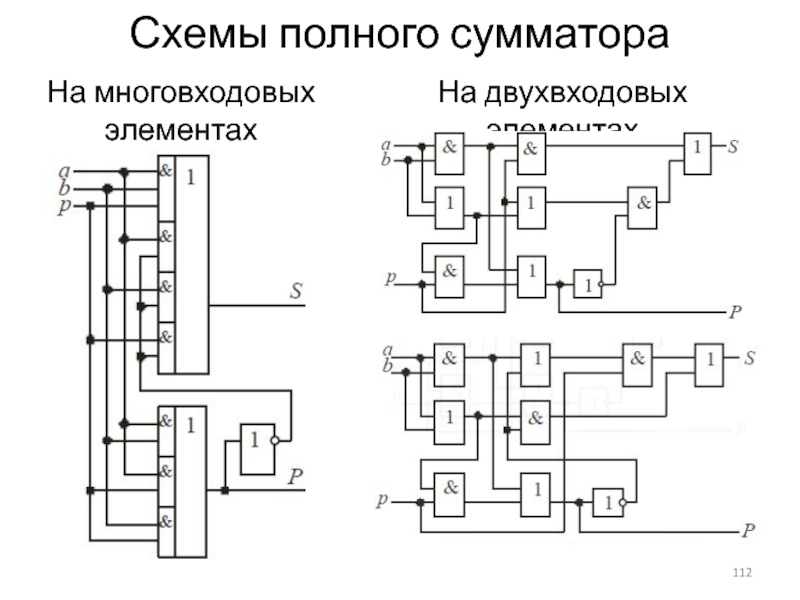
Слайд 112Схемы полного сумматора
На многовходовых элементах
На двухвходовых элементах
Слайд 113Многоразрядные двоичные сумматоры
По способу ввода кодов слагаемых
Последователь-ного действия
Параллель-ного действия
Слайд 115Принцип работы:
1 тактовый импульс:
на входы сумматора поступают из регистров
1 и 2 цифры 1 разряда слагаемых a1 и b1,
из D-триггера на вход подается лог.0.
формируется первый разряд суммы S1, выдаваемый на вход регистра 3, и перенос p2, принимаемый в D-триггер.
2 тактовый импульс:
в регистрах происходит сдвиг на один разряд вправо
на входы сумматора подаются цифры 2 разряда слагаемых a2, b2 и перенос p2,
полученная цифра второго разряда суммы вдвигается в регистр 3,
перенос p3 принимается в триггер и так далее.
Сумматор последовательного действия
Слайд 116Сумматор параллельного действия
Принцип работы:
При подаче слагаемых цифры их разрядов поступают
на соответствующие одноразрядные сумматоры.
Каждый из одноразрядных сумматоров формирует на
своих выходах цифру соответствующего разряда суммы и перенос, передаваемый на вход одноразрядного сумматора следующего (более старшего) разряда.
Слайд 117Повышение быстродействия параллельных сумматоров
При построении схем одноразрядных сумматоров стремятся к
уменьшению числа элементов в цепи между входом, на который поступает
импульс переноса pi, и выходом, на котором формируется передаваемый в следующий разряд импульс переноса pi+1.
В цепях от pi к pi+1 применяют элементы с повышенным быстродействием
Схемы сумматоров следует строить таким образом, чтобы сигналы с выхода каждого логического элемента в цепи от pi к pi+1 поступали на возможно меньшее число других логических элементов
Применяют устройства формирования переносов в параллельной форме
Слайд 118Устройства формирования переносов в параллельной форме
Блок ускоренного переноса:
– производится
формирование переносов в параллельной форме, т.е. одновременно для всех разрядов.
– Переносы из этого блока поступают во все разряды сумматора одновременно.
Слайд 119Десятичные сумматоры. Сумматор для кода 8421
Четырехразрядных двоичный сумматор
Схема коррекции суммы
Схема
формирования переноса