Уравнения, допускающие понижение порядка.

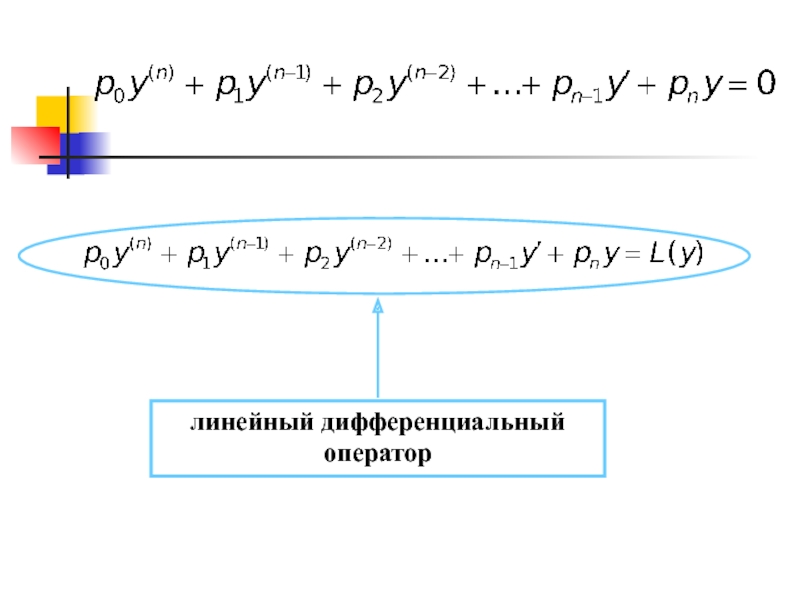
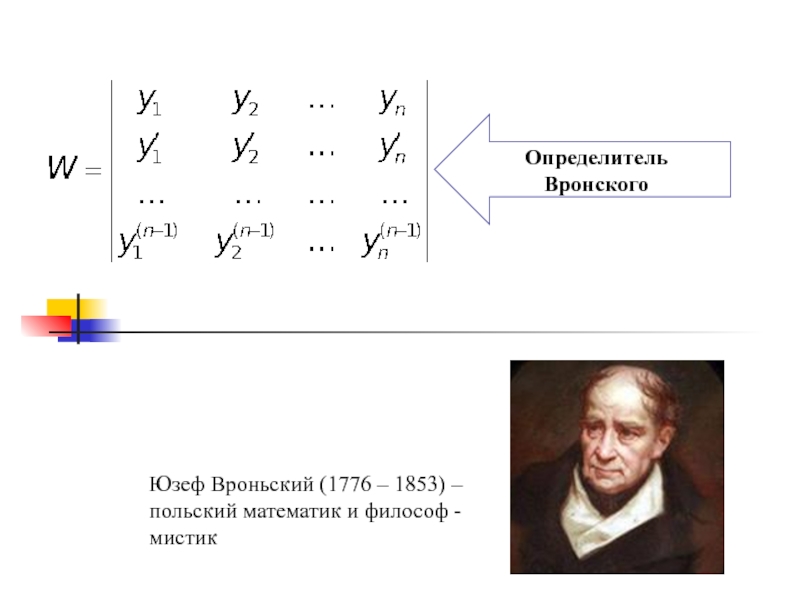
ДУ высших порядков можно записать:


Общее решение ДУ n – ого

Начальные условия для ДУ n – ого порядка задаются в виде:

Решение, получающееся из общего решения при конкретных значениях произвольных постоянных, называется частным решением:

или

если его можно разрешить относительно старшей производной.

на некотором промежутке a < x < b, то решение

………………………………………………

порядка k – 1 включительно

В уравнениях такого типа возможно понижение

соотношением:

Делая обратную подстановку, имеем:

Интегрируя полученное соотношение последовательно

с разделяющимися переменными.
Найдем С1 с помощью начального условия:
Найдем С2 с

замены переменных
3.Уравнения, не содержащие явно независимой переменной

и т.д.

решения данного ДУ остается решить уравнение первого порядка:

(по начальному условию), получим:
- линейное уравнение 1 порядка.

замены переменных
4.Уравнения, не содержащие явно независимой переменной, однородные относительно

функции и ее производных:
Положим:

решение y=0):
Т.к.

При С2=0 в этой записи содержится и y=0.

у и ее производных
вида:


где p0, p1, …,pn –

у и ее производных
вида:


где p0, p1, …,pn –

линейным однородным уравнением,
если f(x) ≠ 0, то уравнение L(y)

функция Су1 (где С – постоянное число) также является его

всякая система n линейно независимых на этом интервале решений уравнения

философ - мистик

Вронского равен нулю.

Теорема. Если функции
линейно независимы, то составленный для

и достаточно, чтобы составленный для них определитель Вронского был не

Теорема. Если

фундаментальная система решений на интервале (a, b), то общее решение ЛОДУ является линейной комбинацией этих решений

где Ci –постоянные коэффициенты.

вида

и известно одно ненулевое решение у = у1,
то

Вывод: для получения общего решения надо подобрать какое-либо частное решение ДУ

= const.





= F(k)

и достаточно, чтобы

т.е.


Характеристическое уравнение

частные решения ДУ, причем:
a) каждому действительному корню соответствует решение ekx;
б)

1) Составляем характеристическое уравнение и находим его корни.

в) каждой паре комплексно – сопряженных корней

характеристического уравнение ставится в соответствие два решения:

и

паре m – кратных комплексно – сопряженных корней
характеристического

3) Составляем линейную комбинацию найденных решений

Эта линейная комбинация и будет являться общим решением исходного линейного однородного дифференциального уравнения с постоянными коэффициентами.