Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ ДЛЯ УМЕНЬШЕНИЯ МУЛЬТИКОЛЛИНЕАРНОСТИ 1 Что вы можете
Содержание
- 1. ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ ДЛЯ УМЕНЬШЕНИЯ МУЛЬТИКОЛЛИНЕАРНОСТИ 1 Что вы можете
- 2. 2Прежде чем сделать это, необходимо подчеркнуть два
- 3. 3Проблема в том, что они имеют неудовлетворительно большие отклонения.ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
- 4. 4Во-вторых, стандартные ошибки и t-тесты остаются в
- 5. 5Проблема мультиколлинеарности обусловлена тем, что дисперсии коэффициентов
- 6. 6Мы сосредоточимся на коэффициенте наклона и рассмотрим
- 7. 7Мы сосредоточимся на коэффициенте наклона и рассмотрим различные компоненты его дисперсии.ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
- 8. 8Мы сосредоточимся на коэффициенте наклона и рассмотрим различные компоненты его дисперсии.ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
- 9. 9Мы сосредоточимся на коэффициенте наклона и рассмотрим
- 10. ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ10Начнем с n, количества наблюдений.
- 11. ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ11Предположим, что
- 12. ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ12Пояснительными переменными
- 13. ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ13Все коэффициенты
- 14. ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ14Материнское образование
- 15. ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ16Наиболее вероятным
- 16. ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ16Вот результат
- 17. ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ17Сравнивая этот
- 18. ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ18Как следствие,
- 19. ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ19Этот пример
- 20. ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ20Если вы
- 21. ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ21Кроме того,
- 22. ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ22You select
- 23. ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ23You then
- 24. ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ(1) Увеличьте количество
- 25. (2) Уменьшите, включив в
- 26. 26Здесь мы добавили в спецификацию фиктивную переменную
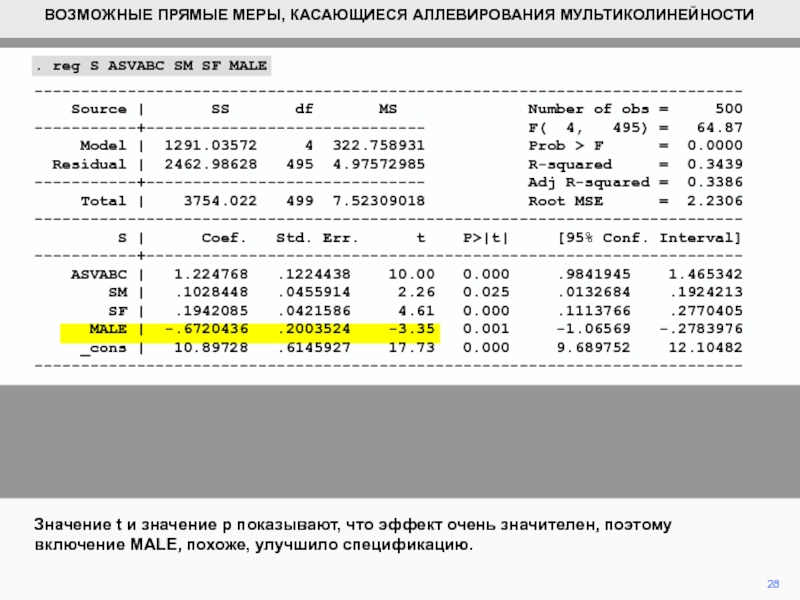
- 27. 27Коэффициент MALE указывает на то, что, контролируя
- 28. 28Значение t и значение p показывают, что
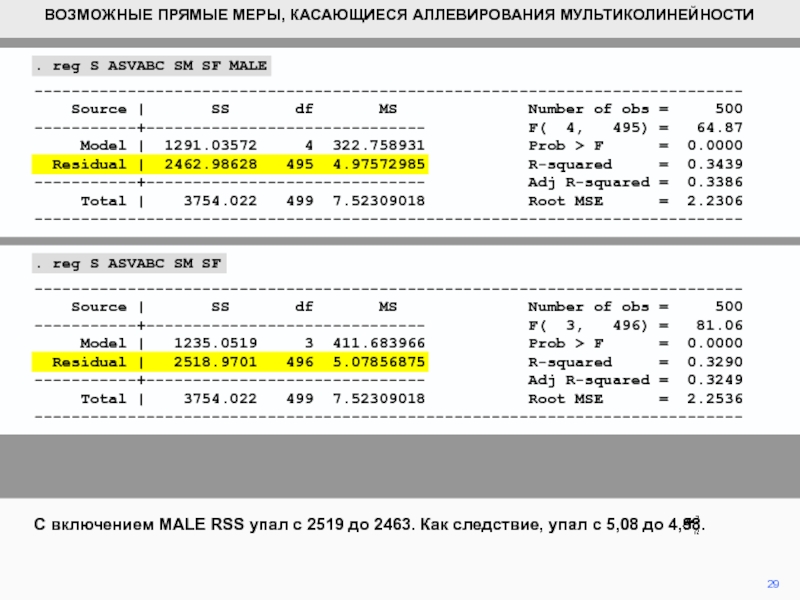
- 29. 29С включением MALE RSS упал с 2519
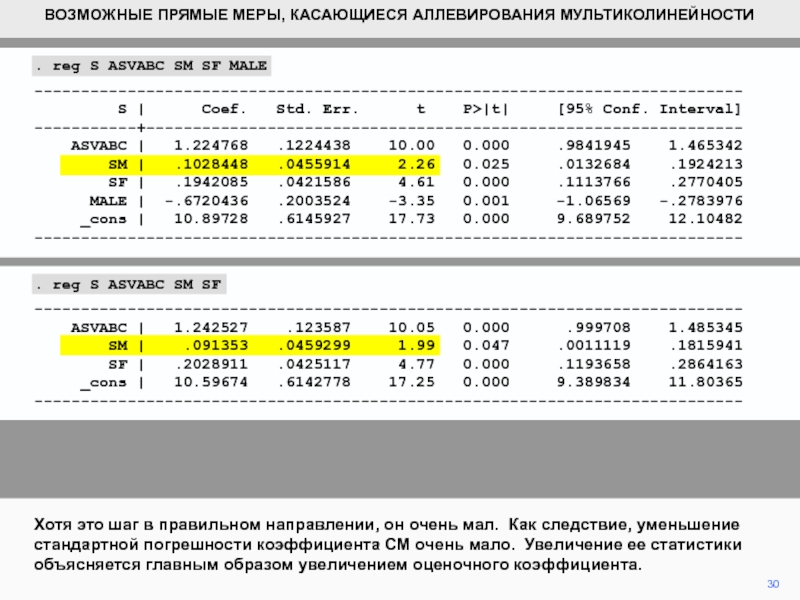
- 30. 30Хотя это шаг в правильном направлении, он
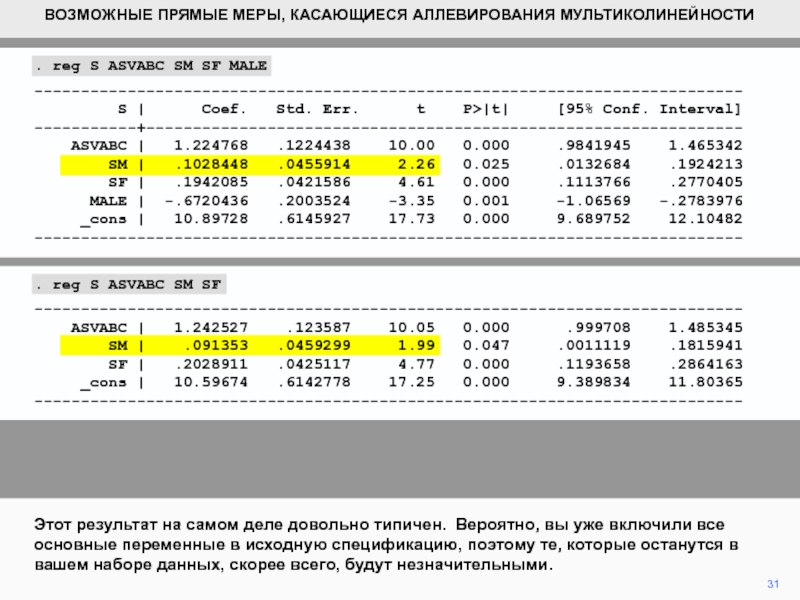
- 31. 31Этот результат на самом деле довольно типичен.
- 32. 32Этот подход может даже иметь эффект, противоположный
- 33. 33Третьим возможным способом уменьшения проблемы многоколлинеарности может
- 34. 34Например, если вы планируете опрос домашних хозяйств
- 35. 35Другая возможность может заключаться в уменьшении корреляции
- 36. Скачать презентанцию
Слайды и текст этой презентации
Слайд 22
Прежде чем сделать это, необходимо подчеркнуть два важных момента. Во-первых,
мультиколлинеарность не приводит к смещению коэффициентов регрессии.
ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ
АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИСлайд 33
Проблема в том, что они имеют неудовлетворительно большие отклонения.
ВОЗМОЖНЫЕ ПРЯМЫЕ
МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
Слайд 44
Во-вторых, стандартные ошибки и t-тесты остаются в силе. Стандартные ошибки
больше, чем они были бы в отсутствие мультиколлинеарности, предупреждая нас,
что оценки регрессии неустойчивы.ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
Слайд 55
Проблема мультиколлинеарности обусловлена тем, что дисперсии коэффициентов неудовлетворительно велики. В
этой последовательности мы рассмотрим возможные прямые методы их сокращения. В
следующей последовательности мы рассмотрим возможные косвенные методы.ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
Слайд 66
Мы сосредоточимся на коэффициенте наклона и рассмотрим различные компоненты его
дисперсии.
ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
Слайд 77
Мы сосредоточимся на коэффициенте наклона и рассмотрим различные компоненты его
дисперсии.
ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
Слайд 88
Мы сосредоточимся на коэффициенте наклона и рассмотрим различные компоненты его
дисперсии.
ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
Слайд 99
Мы сосредоточимся на коэффициенте наклона и рассмотрим различные компоненты его
дисперсии.
.
ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
Слайд 10ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
10
Начнем с n, количества наблюдений.
Слайд 11ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
11
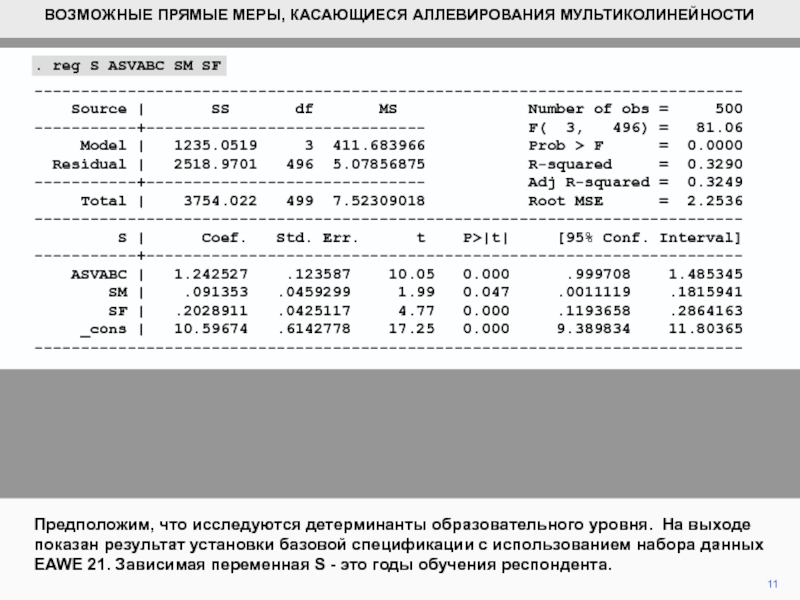
Предположим, что исследуются детерминанты образовательного
уровня. На выходе показан результат установки базовой спецификации с использованием
набора данных EAWE 21. Зависимая переменная S - это годы обучения респондента.. reg S ASVABC SM SF
----------------------------------------------------------------------------
Source | SS df MS Number of obs = 500
-----------+------------------------------ F( 3, 496) = 81.06
Model | 1235.0519 3 411.683966 Prob > F = 0.0000
Residual | 2518.9701 496 5.07856875 R-squared = 0.3290
-----------+------------------------------ Adj R-squared = 0.3249
Total | 3754.022 499 7.52309018 Root MSE = 2.2536
----------------------------------------------------------------------------
S | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
ASVABC | 1.242527 .123587 10.05 0.000 .999708 1.485345
SM | .091353 .0459299 1.99 0.047 .0011119 .1815941
SF | .2028911 .0425117 4.77 0.000 .1193658 .2864163
_cons | 10.59674 .6142778 17.25 0.000 9.389834 11.80365
----------------------------------------------------------------------------
Слайд 12ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
12
Пояснительными переменными являются ASVABC, SM
и SF. ASVABC - это оценка по когнитивной способности, масштабируемая
таким образом, что она имеет среднее значение 0 и стандартное отклонение 1. SM и SF являются годами обучения матери и отца респондента, соответственно.. reg S ASVABC SM SF
----------------------------------------------------------------------------
Source | SS df MS Number of obs = 500
-----------+------------------------------ F( 3, 496) = 81.06
Model | 1235.0519 3 411.683966 Prob > F = 0.0000
Residual | 2518.9701 496 5.07856875 R-squared = 0.3290
-----------+------------------------------ Adj R-squared = 0.3249
Total | 3754.022 499 7.52309018 Root MSE = 2.2536
----------------------------------------------------------------------------
S | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
ASVABC | 1.242527 .123587 10.05 0.000 .999708 1.485345
SM | .091353 .0459299 1.99 0.047 .0011119 .1815941
SF | .2028911 .0425117 4.77 0.000 .1193658 .2864163
_cons | 10.59674 .6142778 17.25 0.000 9.389834 11.80365
----------------------------------------------------------------------------
Слайд 13ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
13
Все коэффициенты регрессии являются положительными,
как и ожидалось, но для SM достаточно просто на уровне
5 процентов.. reg S ASVABC SM SF
----------------------------------------------------------------------------
Source | SS df MS Number of obs = 500
-----------+------------------------------ F( 3, 496) = 81.06
Model | 1235.0519 3 411.683966 Prob > F = 0.0000
Residual | 2518.9701 496 5.07856875 R-squared = 0.3290
-----------+------------------------------ Adj R-squared = 0.3249
Total | 3754.022 499 7.52309018 Root MSE = 2.2536
----------------------------------------------------------------------------
S | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
ASVABC | 1.242527 .123587 10.05 0.000 .999708 1.485345
SM | .091353 .0459299 1.99 0.047 .0011119 .1815941
SF | .2028911 .0425117 4.77 0.000 .1193658 .2864163
_cons | 10.59674 .6142778 17.25 0.000 9.389834 11.80365
----------------------------------------------------------------------------
Слайд 14ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
14
Материнское образование можно разумно считать
мощным детерминантом образовательного уровня. Соответственно, предельное значение коэффициента СМ является
неожиданным.. reg S ASVABC SM SF
----------------------------------------------------------------------------
Source | SS df MS Number of obs = 500
-----------+------------------------------ F( 3, 496) = 81.06
Model | 1235.0519 3 411.683966 Prob > F = 0.0000
Residual | 2518.9701 496 5.07856875 R-squared = 0.3290
-----------+------------------------------ Adj R-squared = 0.3249
Total | 3754.022 499 7.52309018 Root MSE = 2.2536
----------------------------------------------------------------------------
S | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
ASVABC | 1.242527 .123587 10.05 0.000 .999708 1.485345
SM | .091353 .0459299 1.99 0.047 .0011119 .1815941
SF | .2028911 .0425117 4.77 0.000 .1193658 .2864163
_cons | 10.59674 .6142778 17.25 0.000 9.389834 11.80365
----------------------------------------------------------------------------
Слайд 15ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
16
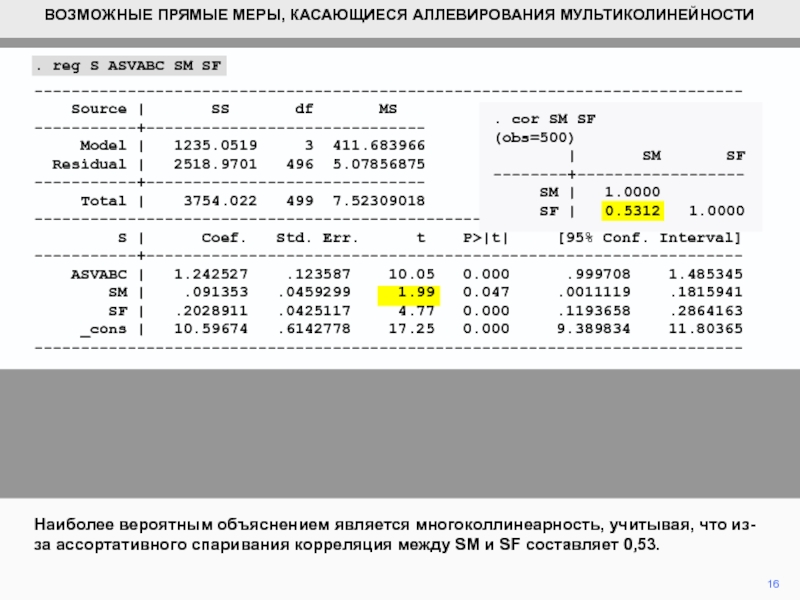
Наиболее вероятным объяснением является многоколлинеарность,
учитывая, что из-за ассортативного спаривания корреляция между SM и SF
составляет 0,53.. reg S ASVABC SM SF
----------------------------------------------------------------------------
Source | SS df MS Number of obs = 500
-----------+------------------------------ F( 3, 496) = 81.06
Model | 1235.0519 3 411.683966 Prob > F = 0.0000
Residual | 2518.9701 496 5.07856875 R-squared = 0.3290
-----------+------------------------------ Adj R-squared = 0.3249
Total | 3754.022 499 7.52309018 Root MSE = 2.2536
----------------------------------------------------------------------------
S | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
ASVABC | 1.242527 .123587 10.05 0.000 .999708 1.485345
SM | .091353 .0459299 1.99 0.047 .0011119 .1815941
SF | .2028911 .0425117 4.77 0.000 .1193658 .2864163
_cons | 10.59674 .6142778 17.25 0.000 9.389834 11.80365
----------------------------------------------------------------------------
. cor SM SF
(obs=500)
| SM SF
--------+------------------
SM | 1.0000
SF | 0.5312 1.0000
Слайд 16ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
16
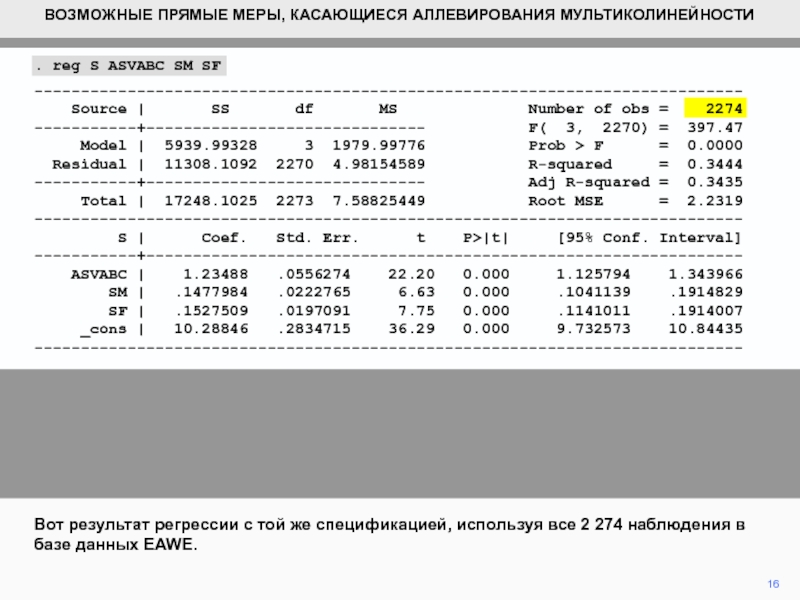
Вот результат регрессии с той
же спецификацией, используя все 2 274 наблюдения в базе данных
EAWE.. reg S ASVABC SM SF
----------------------------------------------------------------------------
Source | SS df MS Number of obs = 2274
-----------+------------------------------ F( 3, 2270) = 397.47
Model | 5939.99328 3 1979.99776 Prob > F = 0.0000
Residual | 11308.1092 2270 4.98154589 R-squared = 0.3444
-----------+------------------------------ Adj R-squared = 0.3435
Total | 17248.1025 2273 7.58825449 Root MSE = 2.2319
----------------------------------------------------------------------------
S | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
ASVABC | 1.23488 .0556274 22.20 0.000 1.125794 1.343966
SM | .1477984 .0222765 6.63 0.000 .1041139 .1914829
SF | .1527509 .0197091 7.75 0.000 .1141011 .1914007
_cons | 10.28846 .2834715 36.29 0.000 9.732573 10.84435
----------------------------------------------------------------------------
Слайд 17ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
17
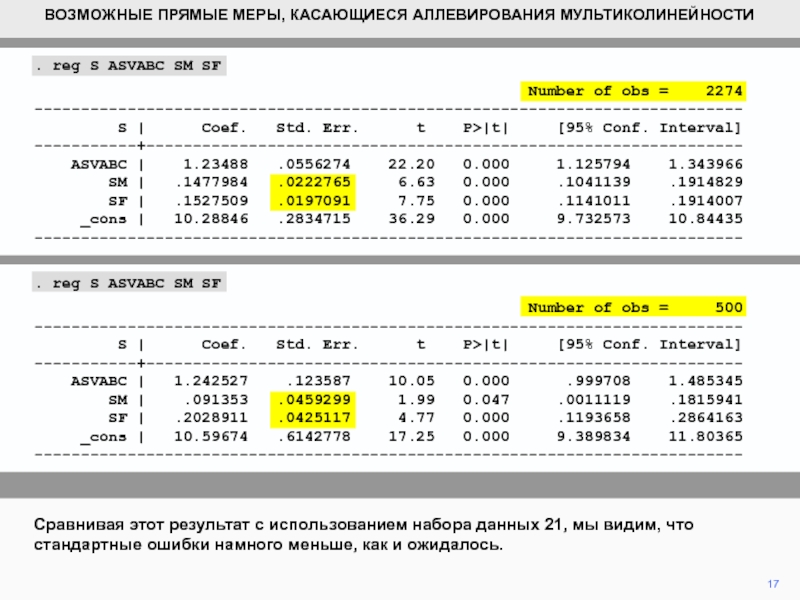
Сравнивая этот результат с использованием
набора данных 21, мы видим, что стандартные ошибки намного меньше,
как и ожидалось.. reg S ASVABC SM SF
Number of obs = 2274
----------------------------------------------------------------------------
S | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
ASVABC | 1.23488 .0556274 22.20 0.000 1.125794 1.343966
SM | .1477984 .0222765 6.63 0.000 .1041139 .1914829
SF | .1527509 .0197091 7.75 0.000 .1141011 .1914007
_cons | 10.28846 .2834715 36.29 0.000 9.732573 10.84435
----------------------------------------------------------------------------
. reg S ASVABC SM SF
Number of obs = 500
----------------------------------------------------------------------------
S | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
ASVABC | 1.242527 .123587 10.05 0.000 .999708 1.485345
SM | .091353 .0459299 1.99 0.047 .0011119 .1815941
SF | .2028911 .0425117 4.77 0.000 .1193658 .2864163
_cons | 10.59674 .6142778 17.25 0.000 9.389834 11.80365
----------------------------------------------------------------------------
Слайд 18ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
18
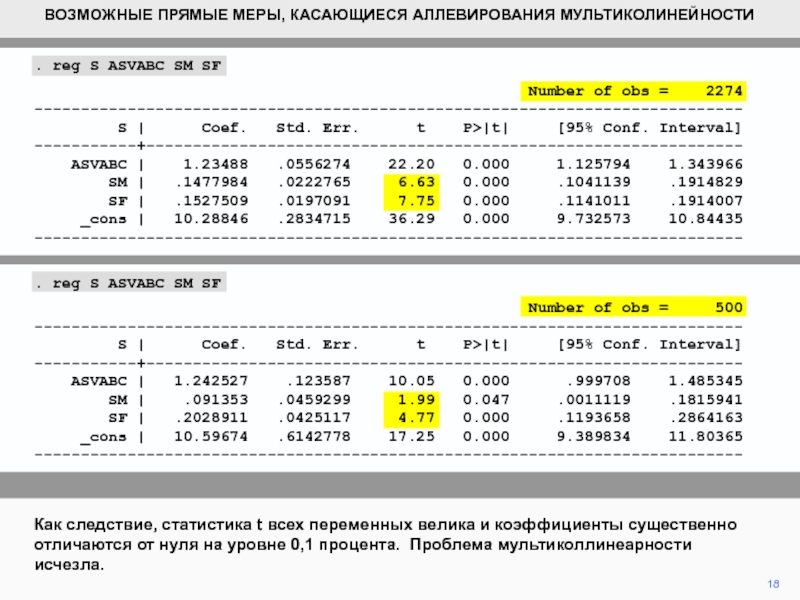
Как следствие, статистика t всех
переменных велика и коэффициенты существенно отличаются от нуля на уровне
0,1 процента. Проблема мультиколлинеарности исчезла.. reg S ASVABC SM SF
Number of obs = 2274
----------------------------------------------------------------------------
S | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
ASVABC | 1.23488 .0556274 22.20 0.000 1.125794 1.343966
SM | .1477984 .0222765 6.63 0.000 .1041139 .1914829
SF | .1527509 .0197091 7.75 0.000 .1141011 .1914007
_cons | 10.28846 .2834715 36.29 0.000 9.732573 10.84435
----------------------------------------------------------------------------
. reg S ASVABC SM SF
Number of obs = 500
----------------------------------------------------------------------------
S | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
ASVABC | 1.242527 .123587 10.05 0.000 .999708 1.485345
SM | .091353 .0459299 1.99 0.047 .0011119 .1815941
SF | .2028911 .0425117 4.77 0.000 .1193658 .2864163
_cons | 10.59674 .6142778 17.25 0.000 9.389834 11.80365
----------------------------------------------------------------------------
Слайд 19ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
19
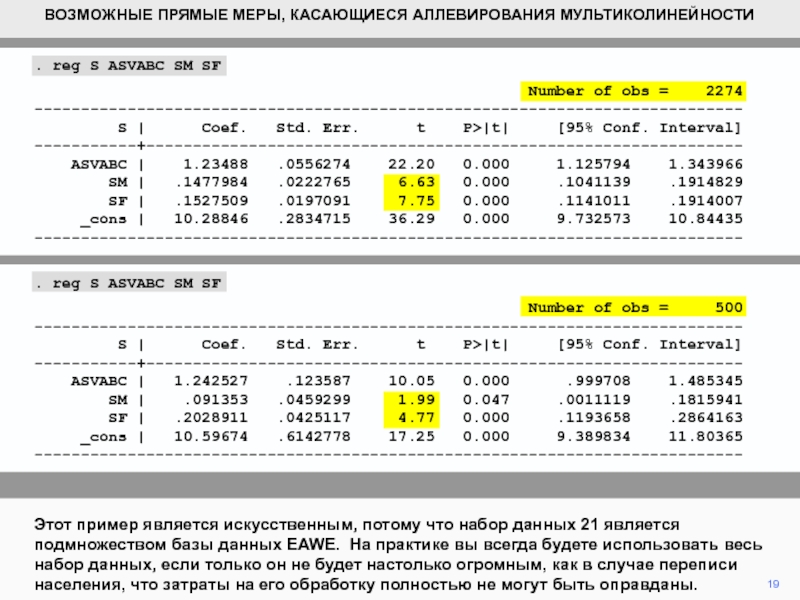
Этот пример является искусственным, потому
что набор данных 21 является подмножеством базы данных EAWE. На
практике вы всегда будете использовать весь набор данных, если только он не будет настолько огромным, как в случае переписи населения, что затраты на его обработку полностью не могут быть оправданы.. reg S ASVABC SM SF
Number of obs = 2274
----------------------------------------------------------------------------
S | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
ASVABC | 1.23488 .0556274 22.20 0.000 1.125794 1.343966
SM | .1477984 .0222765 6.63 0.000 .1041139 .1914829
SF | .1527509 .0197091 7.75 0.000 .1141011 .1914007
_cons | 10.28846 .2834715 36.29 0.000 9.732573 10.84435
----------------------------------------------------------------------------
. reg S ASVABC SM SF
Number of obs = 500
----------------------------------------------------------------------------
S | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
ASVABC | 1.242527 .123587 10.05 0.000 .999708 1.485345
SM | .091353 .0459299 1.99 0.047 .0011119 .1815941
SF | .2028911 .0425117 4.77 0.000 .1193658 .2864163
_cons | 10.59674 .6142778 17.25 0.000 9.389834 11.80365
----------------------------------------------------------------------------
Слайд 20ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
20
Если вы работаете с данными
поперечного сечения (люди, домашние хозяйства, предприятия и т. Д.), И
вы проводите опрос, вы можете увеличить размер выборки, обсудив больший бюджет на стадии планирования.(1) Увеличьте количество наблюдений.
Опросы: увеличение бюджета, использование кластеризации.
Слайд 21ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
21
Кроме того, вы можете сделать
фиксированный бюджет пойти дальше, используя метод, известный как кластеризация. Вы
географически разбиваете страну по почтовому индексу или почтовой области.(1) Увеличьте количество наблюдений.
Опросы: увеличение бюджета, использование кластеризации.
Слайд 22ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
22
You select a number of
these randomly, perhaps using stratified random sampling to make sure
that metropolitan, other urban, and rural areas are properly represented.(1) Увеличьте количество наблюдений.
Опросы: увеличение бюджета, использование кластеризации.
Слайд 23ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
23
You then confine the survey
to the areas selected. This reduces the travel time and
cost of the fieldworkers, allowing them to interview a greater number of respondents.(1) Увеличьте количество наблюдений.
Опросы: увеличение бюджета, использование кластеризации.
.
Слайд 24ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
(1) Увеличьте количество наблюдений.
Опросы: увеличение
бюджета, использование кластеризации.
Временные ряды: используйте ежеквартально вместо годовых данных.
24
Если
вы работаете с данными временных рядов, вы можете увеличить выборку, работая с более короткими интервалами времени для данных, например ежеквартальные или даже ежемесячные данные, а не годовые данные.Слайд 25(2) Уменьшите, включив в модель дополнительные релевантные
переменные
25
Мы могли бы уменьшить дисперсию, добавив в модель больше переменных
и уменьшив дисперсию условия нарушения.ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
Слайд 2626
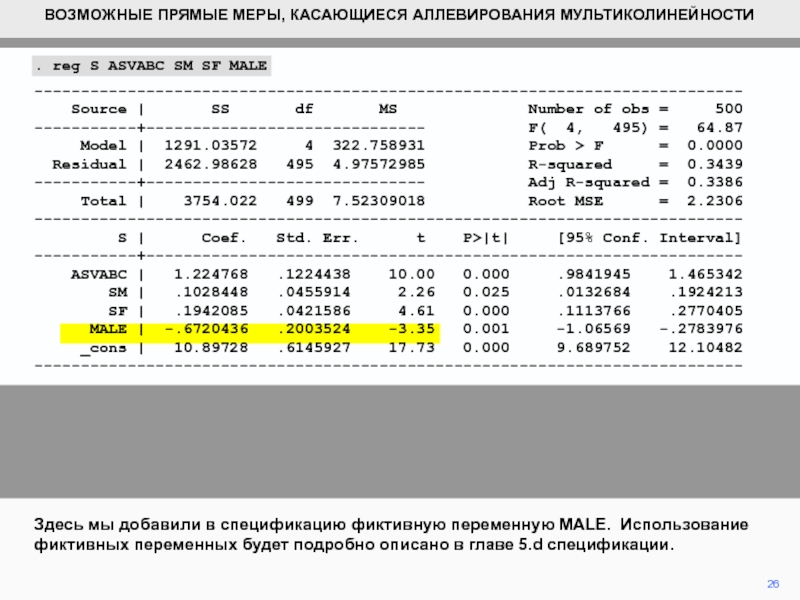
Здесь мы добавили в спецификацию фиктивную переменную MALE. Использование фиктивных
переменных будет подробно описано в главе 5.d спецификации.
. reg S
ASVABC SM SF MALE----------------------------------------------------------------------------
Source | SS df MS Number of obs = 500
-----------+------------------------------ F( 4, 495) = 64.87
Model | 1291.03572 4 322.758931 Prob > F = 0.0000
Residual | 2462.98628 495 4.97572985 R-squared = 0.3439
-----------+------------------------------ Adj R-squared = 0.3386
Total | 3754.022 499 7.52309018 Root MSE = 2.2306
----------------------------------------------------------------------------
S | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
ASVABC | 1.224768 .1224438 10.00 0.000 .9841945 1.465342
SM | .1028448 .0455914 2.26 0.025 .0132684 .1924213
SF | .1942085 .0421586 4.61 0.000 .1113766 .2770405
MALE | -.6720436 .2003524 -3.35 0.001 -1.06569 -.2783976
_cons | 10.89728 .6145927 17.73 0.000 9.689752 12.10482
----------------------------------------------------------------------------
ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
Слайд 2727
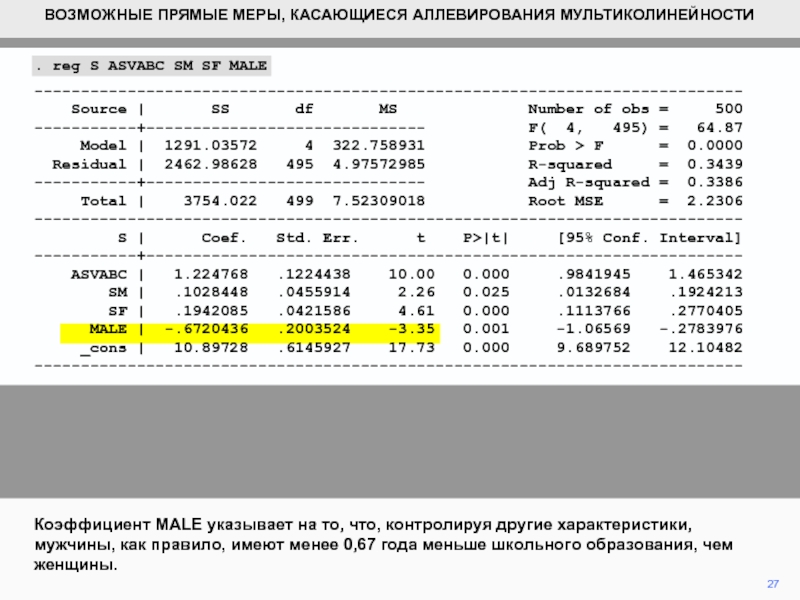
Коэффициент MALE указывает на то, что, контролируя другие характеристики, мужчины,
как правило, имеют менее 0,67 года меньше школьного образования, чем
женщины.. reg S ASVABC SM SF MALE
----------------------------------------------------------------------------
Source | SS df MS Number of obs = 500
-----------+------------------------------ F( 4, 495) = 64.87
Model | 1291.03572 4 322.758931 Prob > F = 0.0000
Residual | 2462.98628 495 4.97572985 R-squared = 0.3439
-----------+------------------------------ Adj R-squared = 0.3386
Total | 3754.022 499 7.52309018 Root MSE = 2.2306
----------------------------------------------------------------------------
S | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
ASVABC | 1.224768 .1224438 10.00 0.000 .9841945 1.465342
SM | .1028448 .0455914 2.26 0.025 .0132684 .1924213
SF | .1942085 .0421586 4.61 0.000 .1113766 .2770405
MALE | -.6720436 .2003524 -3.35 0.001 -1.06569 -.2783976
_cons | 10.89728 .6145927 17.73 0.000 9.689752 12.10482
----------------------------------------------------------------------------
ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
Слайд 2828
Значение t и значение p показывают, что эффект очень значителен,
поэтому включение MALE, похоже, улучшило спецификацию.
. reg S ASVABC SM
SF MALE----------------------------------------------------------------------------
Source | SS df MS Number of obs = 500
-----------+------------------------------ F( 4, 495) = 64.87
Model | 1291.03572 4 322.758931 Prob > F = 0.0000
Residual | 2462.98628 495 4.97572985 R-squared = 0.3439
-----------+------------------------------ Adj R-squared = 0.3386
Total | 3754.022 499 7.52309018 Root MSE = 2.2306
----------------------------------------------------------------------------
S | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
ASVABC | 1.224768 .1224438 10.00 0.000 .9841945 1.465342
SM | .1028448 .0455914 2.26 0.025 .0132684 .1924213
SF | .1942085 .0421586 4.61 0.000 .1113766 .2770405
MALE | -.6720436 .2003524 -3.35 0.001 -1.06569 -.2783976
_cons | 10.89728 .6145927 17.73 0.000 9.689752 12.10482
----------------------------------------------------------------------------
ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
Слайд 2929
С включением MALE RSS упал с 2519 до 2463. Как
следствие, упал с 5,08 до 4,98.
. reg S ASVABC
SM SF MALE----------------------------------------------------------------------------
Source | SS df MS Number of obs = 500
-----------+------------------------------ F( 4, 495) = 64.87
Model | 1291.03572 4 322.758931 Prob > F = 0.0000
Residual | 2462.98628 495 4.97572985 R-squared = 0.3439
-----------+------------------------------ Adj R-squared = 0.3386
Total | 3754.022 499 7.52309018 Root MSE = 2.2306
----------------------------------------------------------------------------
ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
. reg S ASVABC SM SF
----------------------------------------------------------------------------
Source | SS df MS Number of obs = 500
-----------+------------------------------ F( 3, 496) = 81.06
Model | 1235.0519 3 411.683966 Prob > F = 0.0000
Residual | 2518.9701 496 5.07856875 R-squared = 0.3290
-----------+------------------------------ Adj R-squared = 0.3249
Total | 3754.022 499 7.52309018 Root MSE = 2.2536
----------------------------------------------------------------------------
Слайд 3030
Хотя это шаг в правильном направлении, он очень мал. Как
следствие, уменьшение стандартной погрешности коэффициента СМ очень мало. Увеличение ее
статистики объясняется главным образом увеличением оценочного коэффициента.. reg S ASVABC SM SF MALE
----------------------------------------------------------------------------
S | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
ASVABC | 1.224768 .1224438 10.00 0.000 .9841945 1.465342
SM | .1028448 .0455914 2.26 0.025 .0132684 .1924213
SF | .1942085 .0421586 4.61 0.000 .1113766 .2770405
MALE | -.6720436 .2003524 -3.35 0.001 -1.06569 -.2783976
_cons | 10.89728 .6145927 17.73 0.000 9.689752 12.10482
----------------------------------------------------------------------------
ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
. reg S ASVABC SM SF
----------------------------------------------------------------------------
ASVABC | 1.242527 .123587 10.05 0.000 .999708 1.485345
SM | .091353 .0459299 1.99 0.047 .0011119 .1815941
SF | .2028911 .0425117 4.77 0.000 .1193658 .2864163
_cons | 10.59674 .6142778 17.25 0.000 9.389834 11.80365
----------------------------------------------------------------------------
Слайд 3131
Этот результат на самом деле довольно типичен. Вероятно, вы уже
включили все основные переменные в исходную спецификацию, поэтому те, которые
останутся в вашем наборе данных, скорее всего, будут незначительными.. reg S ASVABC SM SF MALE
----------------------------------------------------------------------------
S | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
ASVABC | 1.224768 .1224438 10.00 0.000 .9841945 1.465342
SM | .1028448 .0455914 2.26 0.025 .0132684 .1924213
SF | .1942085 .0421586 4.61 0.000 .1113766 .2770405
MALE | -.6720436 .2003524 -3.35 0.001 -1.06569 -.2783976
_cons | 10.89728 .6145927 17.73 0.000 9.689752 12.10482
----------------------------------------------------------------------------
ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
. reg S ASVABC SM SF
----------------------------------------------------------------------------
ASVABC | 1.242527 .123587 10.05 0.000 .999708 1.485345
SM | .091353 .0459299 1.99 0.047 .0011119 .1815941
SF | .2028911 .0425117 4.77 0.000 .1193658 .2864163
_cons | 10.59674 .6142778 17.25 0.000 9.389834 11.80365
----------------------------------------------------------------------------
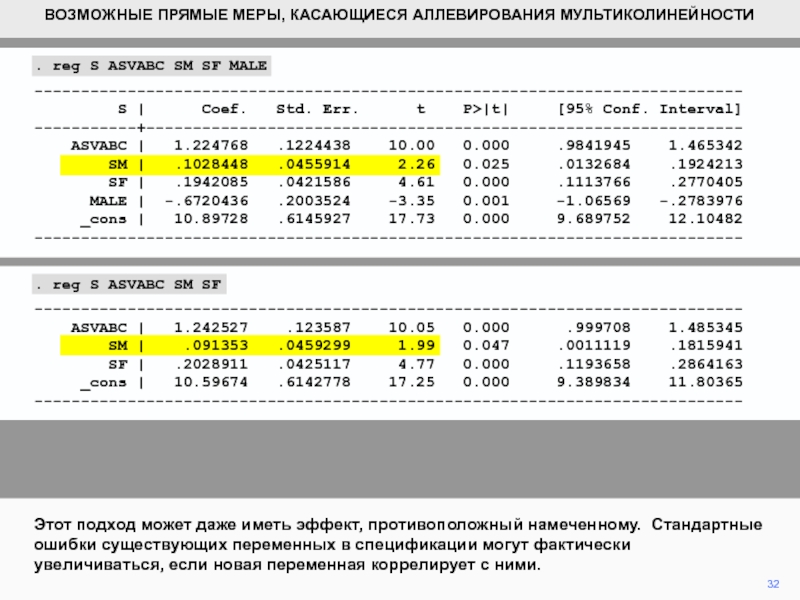
Слайд 3232
Этот подход может даже иметь эффект, противоположный намеченному. Стандартные ошибки
существующих переменных в спецификации могут фактически увеличиваться, если новая переменная
коррелирует с ними.. reg S ASVABC SM SF MALE
----------------------------------------------------------------------------
S | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
ASVABC | 1.224768 .1224438 10.00 0.000 .9841945 1.465342
SM | .1028448 .0455914 2.26 0.025 .0132684 .1924213
SF | .1942085 .0421586 4.61 0.000 .1113766 .2770405
MALE | -.6720436 .2003524 -3.35 0.001 -1.06569 -.2783976
_cons | 10.89728 .6145927 17.73 0.000 9.689752 12.10482
----------------------------------------------------------------------------
ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
. reg S ASVABC SM SF
----------------------------------------------------------------------------
ASVABC | 1.242527 .123587 10.05 0.000 .999708 1.485345
SM | .091353 .0459299 1.99 0.047 .0011119 .1815941
SF | .2028911 .0425117 4.77 0.000 .1193658 .2864163
_cons | 10.59674 .6142778 17.25 0.000 9.389834 11.80365
----------------------------------------------------------------------------
Слайд 3333
Третьим возможным способом уменьшения проблемы многоколлинеарности может быть увеличение вариации
объясняющих переменных. Это возможно только на этапе проектирования обследования.
(3) Увеличить
.ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
Слайд 3434
Например, если вы планируете опрос домашних хозяйств с целью изучения
того, как структура расходов варьируется в зависимости от дохода, вы
должны убедиться, что в выборку включены относительно богатые и относительно бедные домашние хозяйства, а также домохозяйства со средним доходом.ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
(3) Увеличить .
Слайд 3535
Другая возможность может заключаться в уменьшении корреляции между объясняющими переменными.
Опять же, это возможно только на этапе проектирования опроса, и
даже тогда это редко возможно с экономическими данными.ВОЗМОЖНЫЕ ПРЯМЫЕ МЕРЫ, КАСАЮЩИЕСЯ АЛЛЕВИРОВАНИЯ МУЛЬТИКОЛИНЕЙНОСТИ
(4) Уменьшить