Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Вписанная окружность
Содержание
- 1. Вписанная окружность
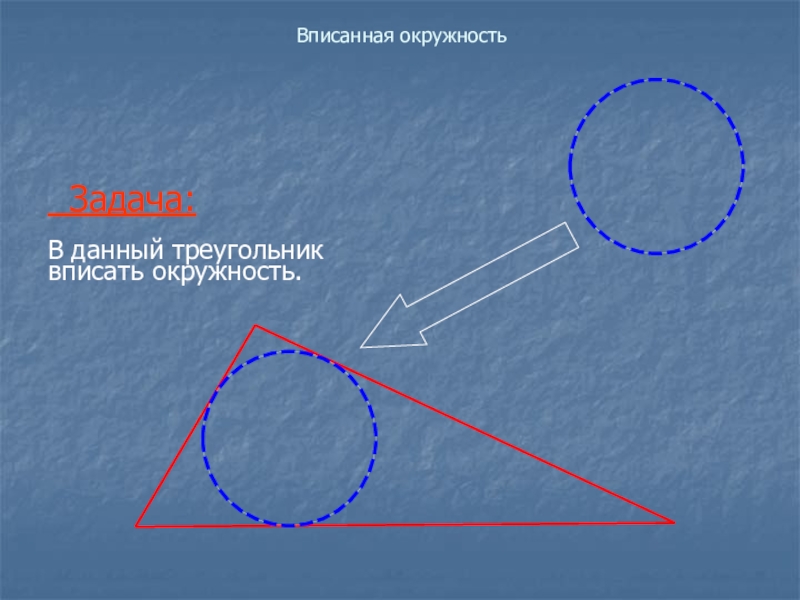
- 2. Вписанная окружность Задача:В данный треугольник вписать окружность.
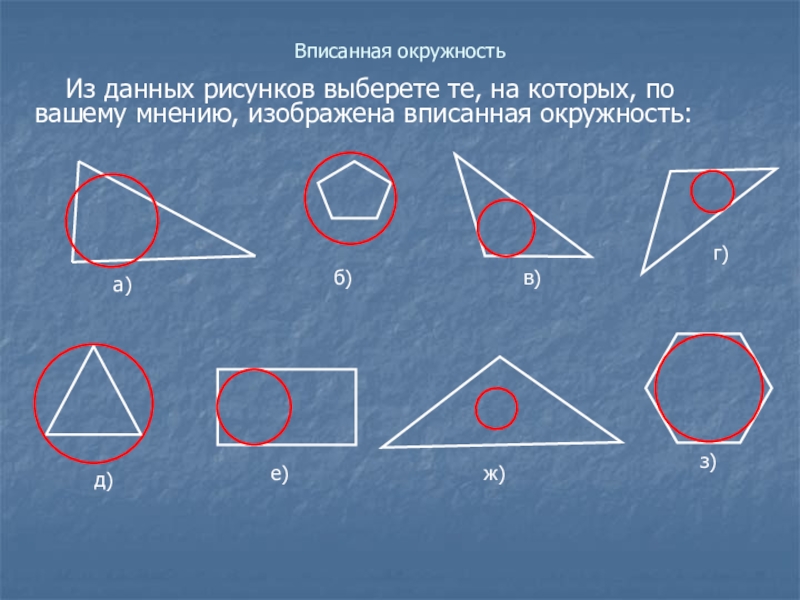
- 3. Вписанная окружностьИз данных рисунков выберете те, на которых, по вашему мнению, изображена вписанная окружность:д)б)в)г)е)ж)а)з)
- 4. Вписанная окружностьОпределение:Окружность называется вписанной в многоугольник, если она касается всех его сторон.
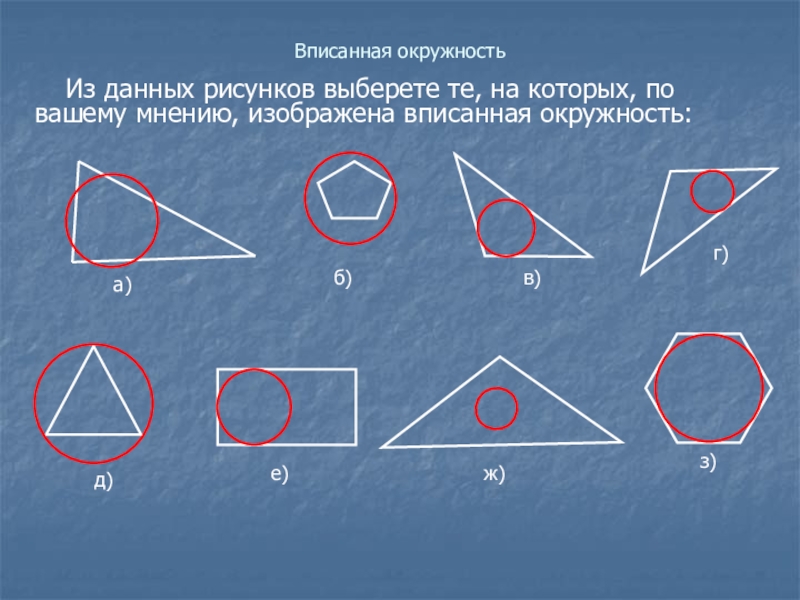
- 5. Вписанная окружностьИз данных рисунков выберете те, на которых, по вашему мнению, изображена вписанная окружность:д)б)в)г)е)ж)з)
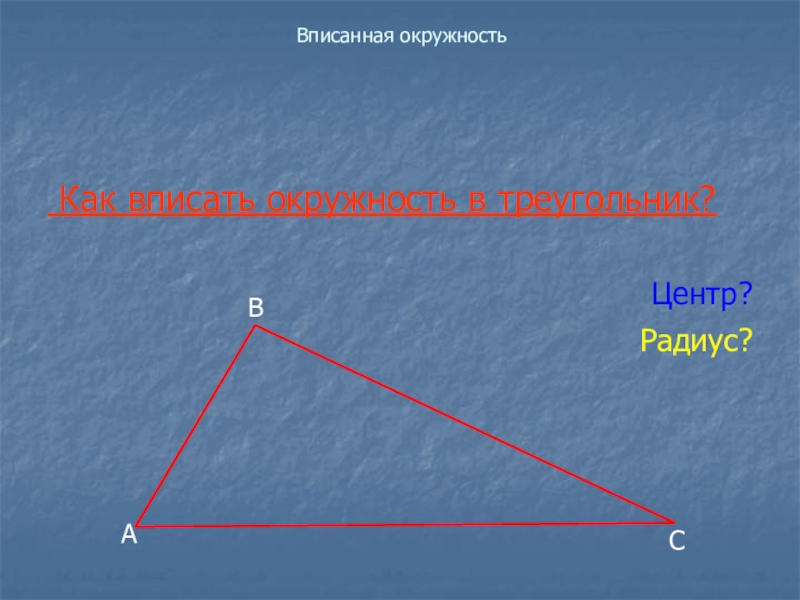
- 6. Вписанная окружность Как вписать окружность в треугольник?Центр?Радиус?АВС
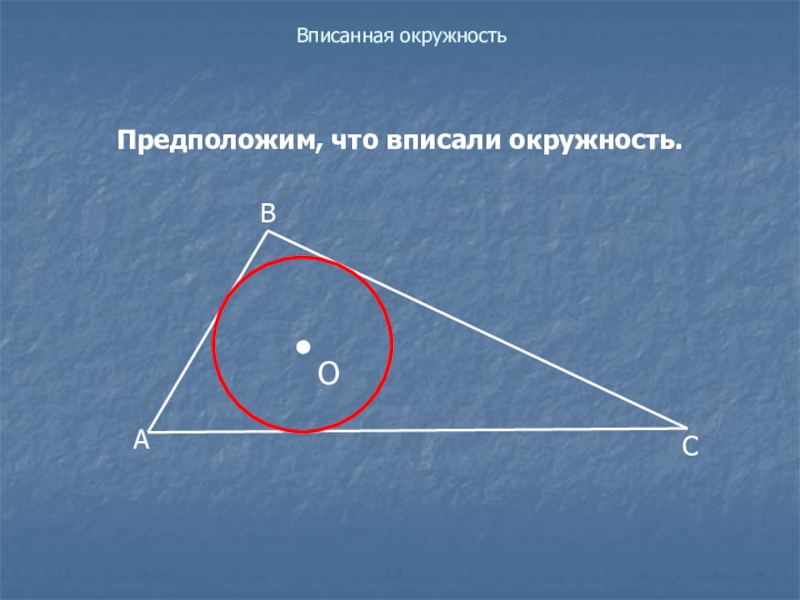
- 7. Вписанная окружностьПредположим, что вписали окружность.
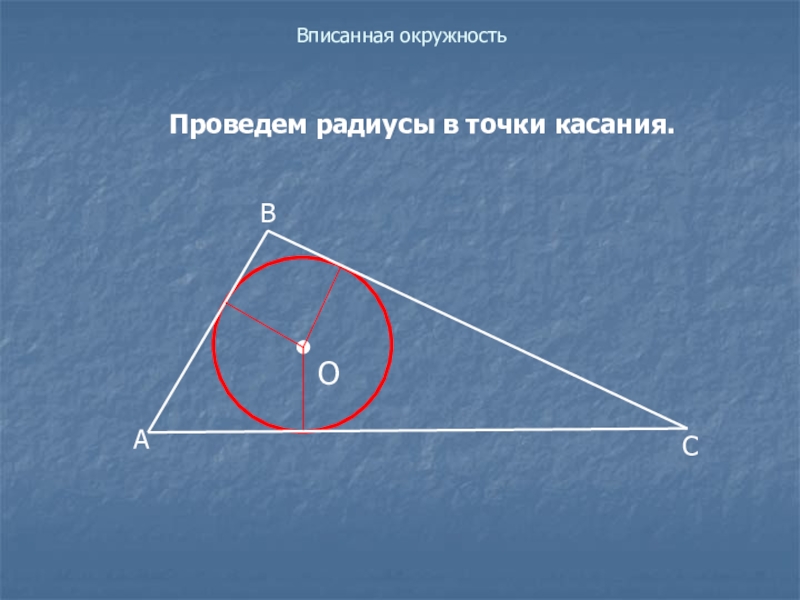
- 8. Вписанная окружностьОПроведем радиусы в точки касания.
- 9. Вписанная окружностьО
- 10. Вписанная окружностьО
- 11. Вписанная окружностьО
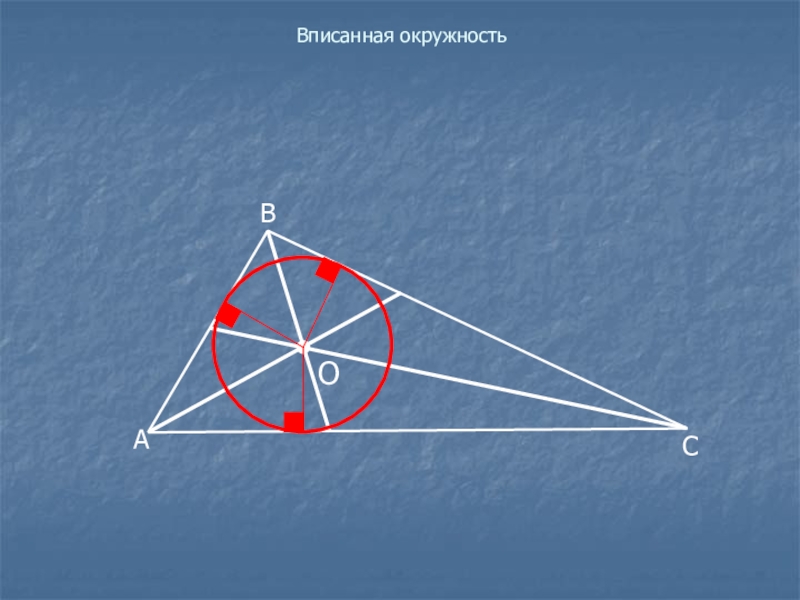
- 12. Вписанная окружностьТаким образом, центр вписанной окружности –
- 13. Вписанная окружностьДля того, чтобы вписать окружность в
- 14. Вписанная окружность
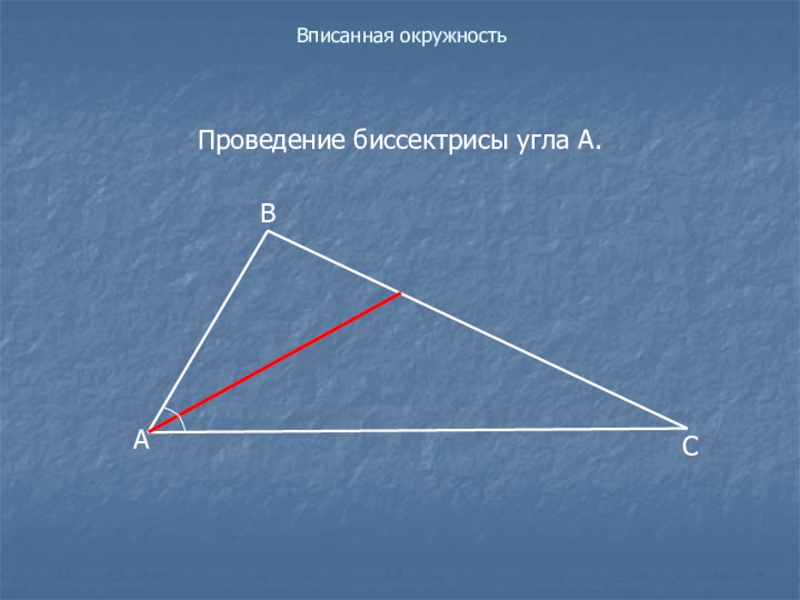
- 15. Вписанная окружностьПроведение биссектрисы угла А.
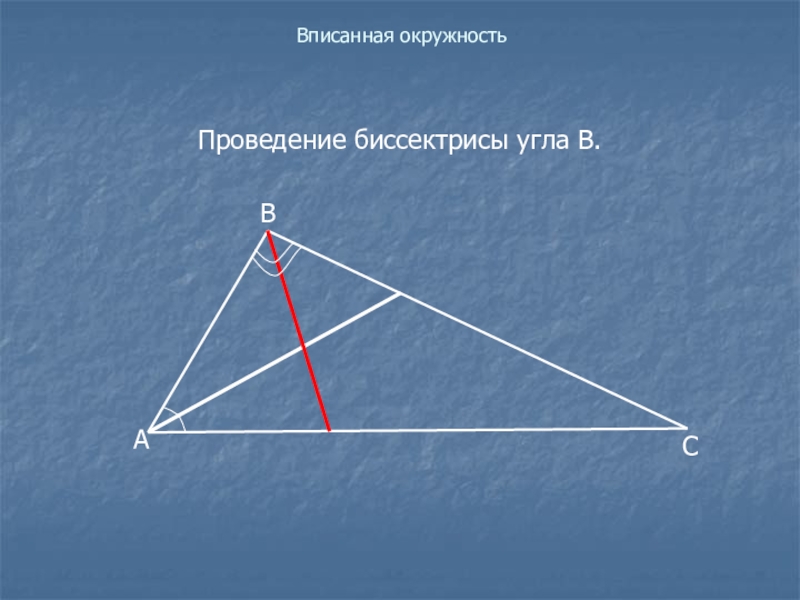
- 16. Вписанная окружностьПроведение биссектрисы угла В.
- 17. Вписанная окружностьПроведение биссектрисы угла С.
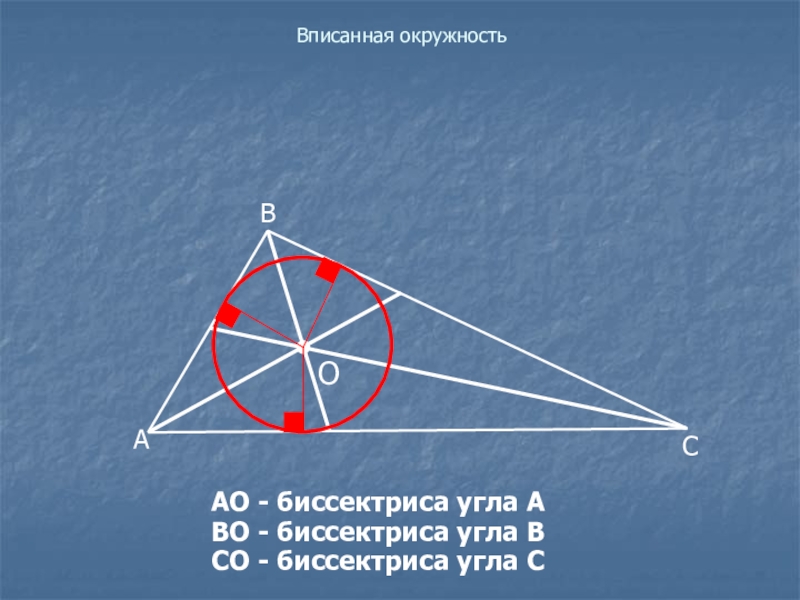
- 18. Вписанная окружностьТочка О - центр вписанной окружности.О
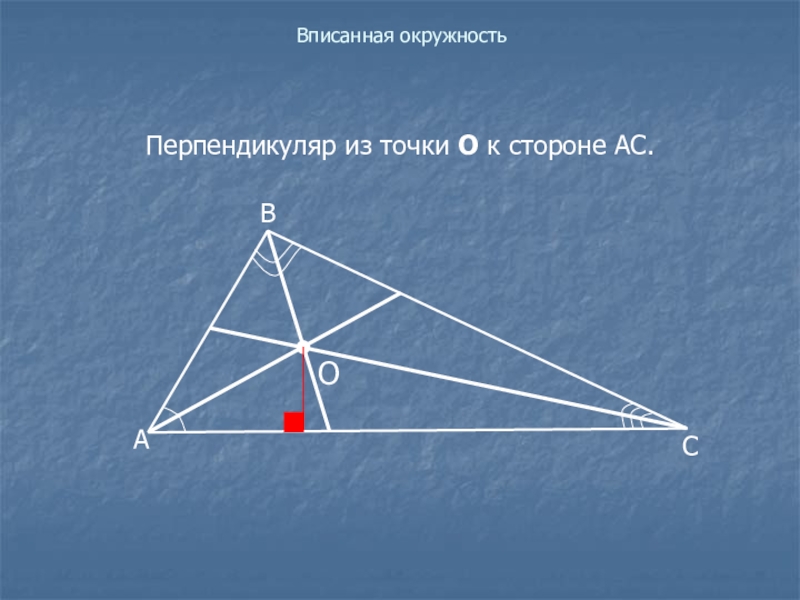
- 19. Вписанная окружностьПерпендикуляр из точки О к стороне АС.
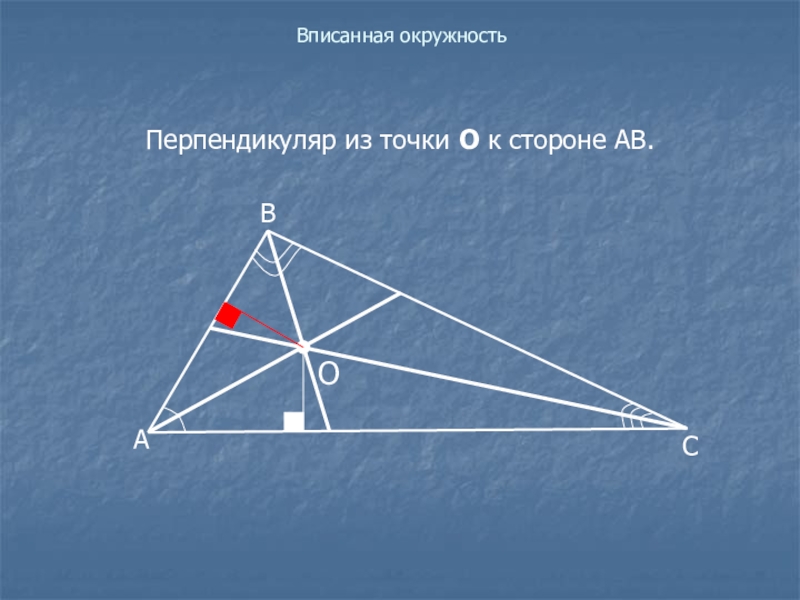
- 20. Вписанная окружностьПерпендикуляр из точки О к стороне АВ.
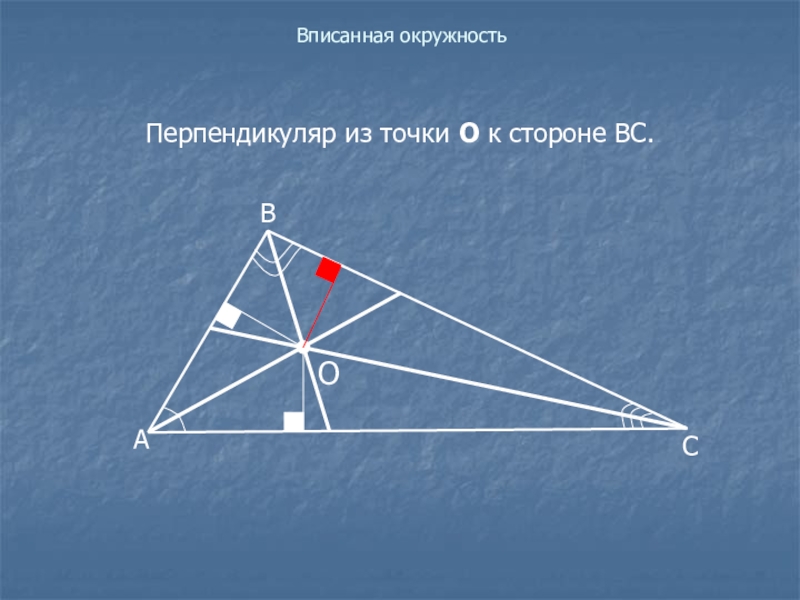
- 21. Вписанная окружностьПерпендикуляр из точки О к стороне
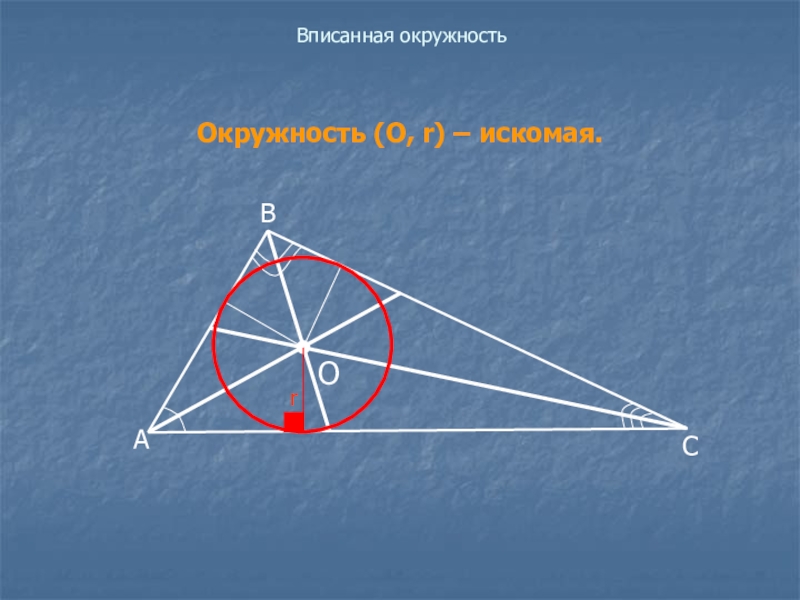
- 22. Вписанная окружностьОкружность (О, r) – искомая.r
- 23. Домашнее задание:Изучить презентацию или прочитать в учебнике
- 24. Скачать презентанцию
Вписанная окружность Задача:В данный треугольник вписать окружность.
Слайды и текст этой презентации
Слайд 3Вписанная окружность
Из данных рисунков выберете те, на которых, по вашему
мнению, изображена вписанная окружность:
Слайд 4Вписанная окружность
Определение:
Окружность называется вписанной в многоугольник, если она касается всех
его сторон.
Слайд 5Вписанная окружность
Из данных рисунков выберете те, на которых, по вашему
мнению, изображена вписанная окружность:
д)
б)
в)
г)
е)
ж)
з)
Слайд 12Вписанная окружность
Таким образом,
центр вписанной окружности – это точка пересечения
биссектрис треугольника,
радиус – это расстояние от центра окружности до
сторон треугольника.Слайд 13Вписанная окружность
Для того, чтобы вписать окружность в треугольник, надо:
1). Найти
точку пересечения биссектрис треугольника (центр окружности);
2). Опустить перпендикуляры из центра
окружности к сторонам треугольника (радиус окружности);3). Провести окружность.
Слайд 23Домашнее задание:
Изучить презентацию или прочитать в учебнике п.77 на с.
178-180;
Выучить алгоритм построения вписанной окружности в треугольник + построить вписанную
окружность по образцу слайдов №14-22 (можно в д/з);Решить №689
Д/з прислать к 28.04. до 15.00