Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Вычисление индуктивности 1). Найти индукцию магнитного поля, как функцию тока:
Содержание
- 1. Вычисление индуктивности 1). Найти индукцию магнитного поля, как функцию тока:
- 2. Пример. Вычисление индуктивности соленоида. 1). Рассмотрим соленоид
- 3. Интеграл по контуру ABCDA можно представить в
- 4. 2). Магнитный поток сквозь один виток соленоида
- 5. Взаимная индукция.Рассмотрим два неподвижных контура (1 и
- 6. При протекании в контуре 2 тока I2
- 7. Коэффициенты пропорциональности L12 и L21 называются взаимной
- 8. Энергия магнитного поля Рассмотрим контур индуктивностью L,
- 9. Энергия магнитного поля, связанного с контуром, равна
- 10. Введем понятие объемной плотности энергии: Выражение для
- 11. Магнитное поле в веществе Если во внешнее
- 12. Суммарный магнитный момент единицы объема называется намагниченностью
- 13. Циркуляция вектора намагниченности J.Циркуляция вектора намагниченности по
- 14. Циркуляция вектора напряженности магнитного поля по
- 15. Связь между векторами B и H.где - магнитная проницаемость среды. Для диамагнетиков Для парамагнетиков
- 16. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Вычисление индуктивности
1). Найти индукцию магнитного поля, как функцию тока:
B=B(I).
связью магнитного потока и силы токаСлайд 2Пример. Вычисление индуктивности соленоида.
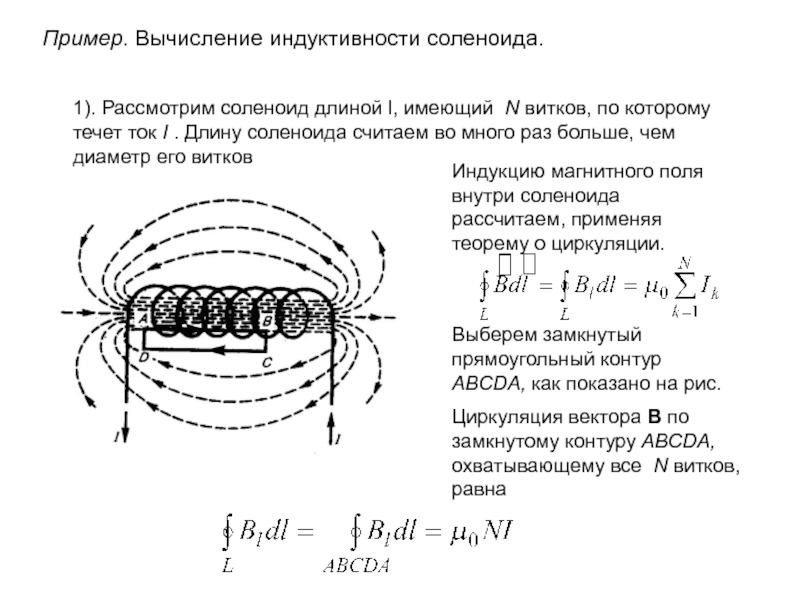
1). Рассмотрим соленоид длиной l, имеющий
N витков, по которому течет ток I . Длину соленоида
считаем во много раз больше, чем диаметр его витковИндукцию магнитного поля внутри соленоида рассчитаем, применяя теорему о циркуляции.
Выберем замкнутый прямоугольный контур ABCDA, как показано на рис.
Циркуляция вектора B по замкнутому контуру ABCDA, охватывающему все N витков, равна
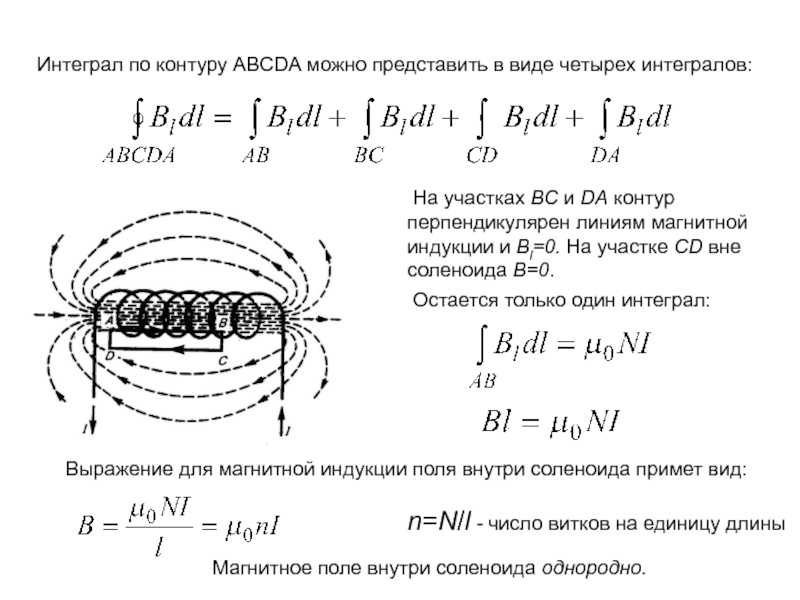
Слайд 3Интеграл по контуру ABCDA можно представить в виде четырех интегралов:
На участках ВС и DA контур перпендикулярен линиям магнитной
индукции и Bl=0. На участке CD вне соленоида B=0. Остается только один интеграл:
Выражение для магнитной индукции поля внутри соленоида примет вид:
n=N/l - число витков на единицу длины
Магнитное поле внутри соленоида однородно.
Слайд 42). Магнитный поток сквозь один виток соленоида площадью S равен
Полный
магнитный поток, пронизывающий N витков, равен
3). Вычислим индуктивность соленоида
V=Sl
объем соленоида.Для соленоида с сердечником:
- магнитная проницаемость среды
Слайд 5Взаимная индукция.
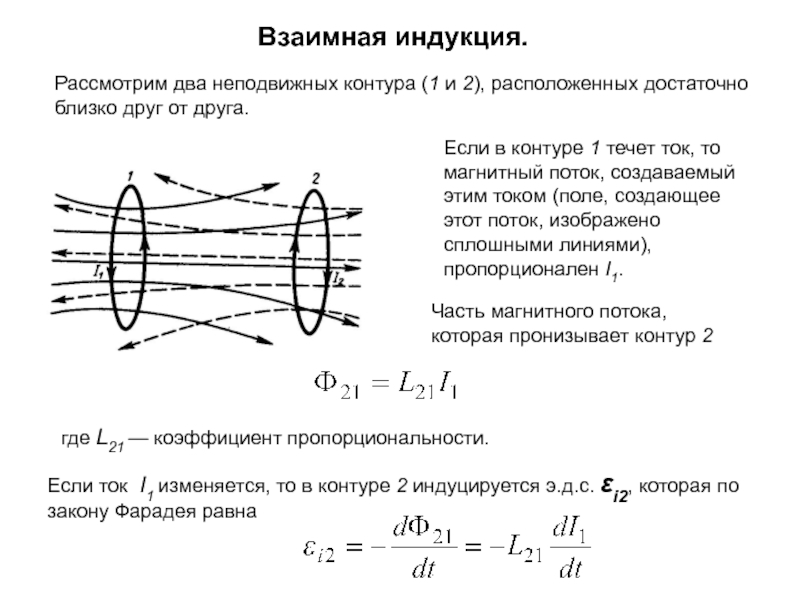
Рассмотрим два неподвижных контура (1 и 2), расположенных достаточно
близко друг от друга.
Если в контуре 1 течет ток,
то магнитный поток, создаваемый этим током (поле, создающее этот поток, изображено сплошными линиями), пропорционален I1. Часть магнитного потока, которая пронизывает контур 2
где L21 — коэффициент пропорциональности.
Если ток I1 изменяется, то в контуре 2 индуцируется э.д.с. i2, которая по закону Фарадея равна
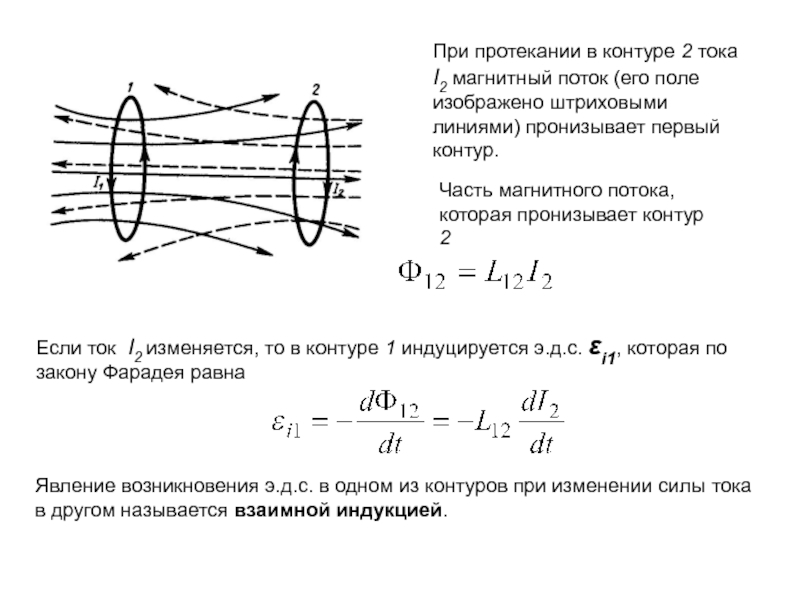
Слайд 6При протекании в контуре 2 тока I2 магнитный поток (его
поле изображено штриховыми линиями) пронизывает первый контур.
Часть магнитного потока,
которая пронизывает контур 2Если ток I2 изменяется, то в контуре 1 индуцируется э.д.с. i1, которая по закону Фарадея равна
Явление возникновения э.д.с. в одном из контуров при изменении силы тока в другом называется взаимной индукцией.
Слайд 7Коэффициенты пропорциональности L12 и L21 называются взаимной индуктивностью контуров.
Коэффициенты
L12 и L21 зависят от геометрической формы, размеров, взаимного расположения
контуров и от магнитной проницаемости окружающей контуры среды.При отсутствии ферромагнетиков
(Теорема взаимности).
Единица взаимной индуктивности — генри (Гн)
Слайд 8Энергия магнитного поля
Рассмотрим контур индуктивностью L, по которому течет
ток I.
Магнитный поток, создаваемый полем этого тока
При изменении
тока на dI магнитный поток изменяется на dДля изменения магнитного потока необходимо совершить работу
Тогда работа по созданию магнитного потока Ф будет равна
Слайд 9Энергия магнитного поля, связанного с контуром, равна
Выразим энергию магнитного
поля непосредственно через индукцию магнитного поля B на примере соленоида.
Так
как Индукция магнитного поля соленоида равна
Выразим
Подставим в выражение для энергии магнитного поля
Слайд 10Введем понятие объемной плотности энергии:
Выражение для объемной плотности энергии
магнитного поля получено для однородного поля, но оно справедливо и
для неоднородных полей.Слайд 11Магнитное поле в веществе
Если во внешнее магнитное поле
внести вещество, то поле изменяется,т ак как всякое вещество способно
под действием магнитного поля приобретать магнитный момент. Это можно объяснить тем, что каждый движущийся вокруг ядра атома электрон представляет собой элементарный круговой ток.
В отсутствие внешнего поля орбиты молекулярных токов, а, следовательно, и их магнитные моменты
ориентированы хаотически в пространстве так, что вещество не проявляет никаких магнитных свойств.
При наложении внешнего магнитного поля моменты ориентируются вдоль силовых линий этого поля - вещество намагничивается.
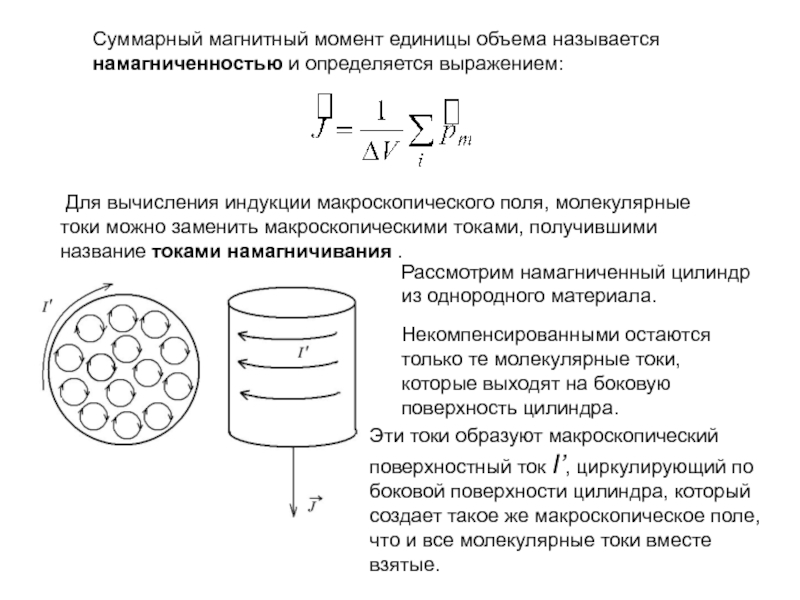
Слайд 12Суммарный магнитный момент единицы объема называется намагниченностью и определяется выражением:
Для вычисления индукции макроскопического поля, молекулярные токи можно заменить
макроскопическими токами, получившими название токами намагничивания . Рассмотрим намагниченный цилиндр из однородного материала.
Некомпенсированными остаются только те молекулярные токи, которые выходят на боковую поверхность цилиндра.
Эти токи образуют макроскопический поверхностный ток I’, циркулирующий по боковой поверхности цилиндра, который создает такое же макроскопическое поле, что и все молекулярные токи вместе взятые.
Слайд 13Циркуляция вектора намагниченности J.
Циркуляция вектора намагниченности по произвольному замкнутому контуру
равна алгебраической сумме токов намагничивания, охватываемых этим контуром:
Напряженность магнитного поля
H. Циркуляция вектора B, определяется не только токами проводимости, но и токами намагничивания
Выражая ток намагничивания через циркуляцию вектора намагниченности, получим
Величину, стоящую в скобках, называют напряженностью магнитного поля:
Слайд 14 Циркуляция вектора напряженности магнитного поля по произвольному замкнутому контуру
равна алгебраической сумме токов проводимости, охватываемых этим контуром.
Размерность напряженности магнитного
поля Вектор намагниченности и напряженность магнитного поля связаны следующим соотношением:
где - магнитная восприимчивость, зависящая от свойств магнетика.
<0 для диамагнетиков
>0 для парамагнетиков