Вычислительно стойкие системы шифрования

такой системы возможно, но даже наилучший
алгоритм вскрытия требует необозримо

большого времени
или необозримо большой памяти устройств, с помощью которых
проводится криптоанализ

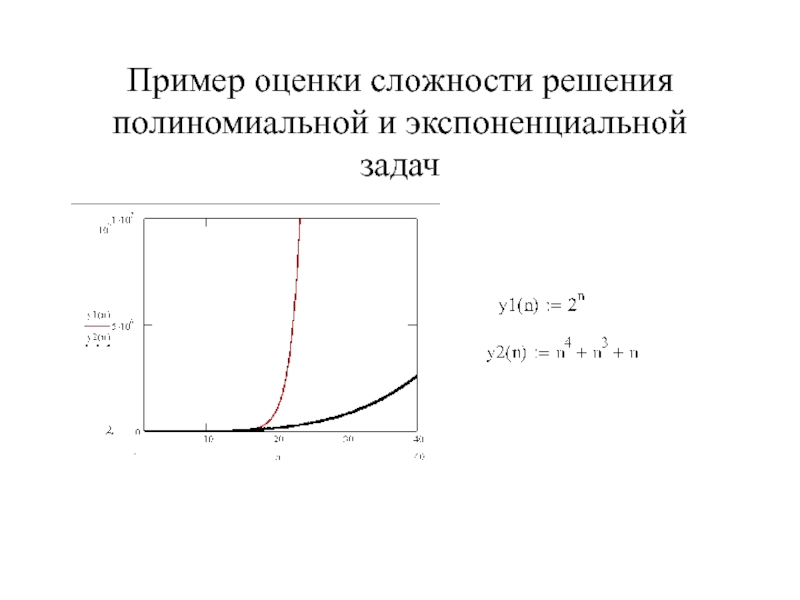
Время криптоанализа определяется:
-Сложностью алгоритма дешифрования;
-Быстродействием вычислительных устройств,
осуществляющих дешифрование

+k1nd-2….n
Простые алгоритмы – это задачи полиномиальной сложности
Nопер=polynom(n), N=k1nd+k2nd-1

+k1nd-2….n

Сложные алгоритмы- это задачи экспоненциальной сложности

Nопер=akn , a,k>0

NP-задачи (недетерминистско полиномиальные) это такие
задачи для которых пока не известны алгоритмы решения
с полиномиальной сложностью, однако если решение
найдено, то проверка его правильности –
задача полиномиальной сложности

криптоанализа должна соответствовать
сложности решения сложной задачи
Основные подходы к криптоанализу:
Тотальный

перебор ключей
Анализ статистических особенностей криптограмм
Линейный криптоанализ
Дифференциальный криптоанализ
Другие

Быстродействие вычислительных устройств 1010- 1012 операций/с

Быстродействие ЭВМ увеличивается в 4 раза каждые 3 года

бит
При N=256 бит Sk= 2256 = 1.18*1077
Время полного перебора Тп=Sk/V,
Если

V=109 ключей в секунду, то Тп =1068 сек =
=3.3*1060 лет!

В году 3.1536*107 секунд

21 1 10 12
Гамма:

+ 25 3 27 6
Криптограмма: нгдс 14 4 5 18
Гамма - 25 3 27 6
-11 1 -22 12
Расшифров. текст: файл 21 1 10 12

+

то система шифрования, использующая этот способ, будет абсолютно стойкой.
2. Операции

зашифрования, расшифрования просты в реализации.
3. При шифровании информации способом гаммирования не происходит размножение ошибок при расшифровании криптограммы, из-за помех возникающих в канале связи.
4. Использование одного и того же отрезка гаммы для шифрования различных сообщений, называемое в криптографии перекрытием шифра, приводит к возможности простого дешифрования сообщений без знания ключа.
5. Способ требует синхронизации гамм на передаче и приеме.

и взаимонезависимы, то система шифрования, использующая данный способ, будет абсолютно

стойкой.

2. В отличие от способа гаммирования, реализация данного способа шифрования более сложна, что определяется необходимостью построения управляемого узла перестановки с m выходами.

3. При шифровании методом замены не происходит размножение ошибок, возникающих в канале связи из-за помех.

4. Перекрытие шифра, т е. шифрование одной и той же таблицей разных сообщений, не приводит к простому и однозначному дешифрованию, как в способе гаммирования. Однако стойкость способа снижается, т. к. повторяющиеся замены дают возможность проведения криптоанализа на основе частот повторения букв криптограммы.

входами и

ключе шифруется несколько блоков, при этом необходимые и достаточные условия

АССШ не выполняются.
2. Реализация блочных шифров на современном уровне развития элементной базы и вычислительной техники не представляет больших трудностей и может быть осуществлена как программным, так и аппаратным путем.
3. Характерное свойство блочных шифров - размножение ошибок, возникающих в канале связи, что является следствием нелинейности используемого преобразования и влиянием каждого символа криптограмм на все символы блока сообщения
4. Перекрытие шифра имеет место, однако криптоанализ затруднен ввиду большой длины блока. Статистические связи между блоками практически отсутствуют, что не позволяет эффективно использовать криптоанализ на основе частот повторения блоков.
5. Нет необходимости в передаче специальной синхро-последовательности для синхронизации шифраторов. Для синхронизации достаточна лишь цикловая синхронизация передаваемых блоков.