Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Взаимосвязи между двумя переменными
Содержание
- 1. Взаимосвязи между двумя переменными
- 2. Типы переменных и гипотезыНезависимые переменные – Х1
- 3. Ассоциация и причина Одна переменная причина другой
- 4. Ассоциации и скрытые признакиразмер обуви и скорость
- 5. Причинно-следственная связь: характеристикиСила ассоциации (позволяет ли величина
- 6. Номинальная + номинальнаястолбчатые диаграммытаблицы сопряженности, анализ условных распределениймеры ассоциации: лямбда, гамма, фиэкстраполяция: хи-квадрат
- 7. Номинальная + интервальнаябокс-плотыравнение средних значениймера ассоциации: этаэкстраполяция: t test
- 8. Интервальная + интервальнаяточечная диаграммамера ассоциации: корреляциярегрессия
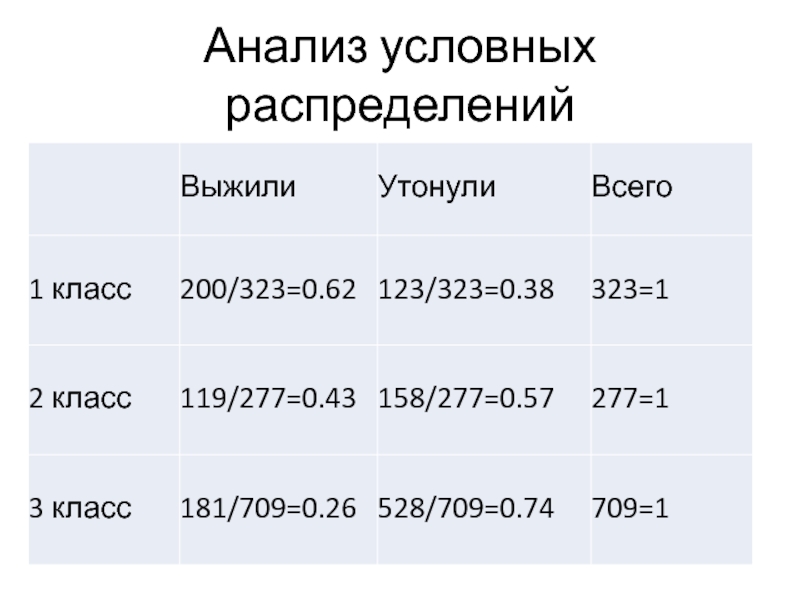
- 9. Анализ условных распределений
- 10. Анализ условных распределений
- 11. Статистическая значимость взаимосвязиЗначимость показывает вероятность (p-value) того,
- 12. Интерпретация (p) статистической значимости p < 0.01
- 13. Меры парной ассоциации Сила - насколько сильно
- 14. Фи [Cramer’s phi]Номинальная-номинальная; Cramer's phi = 0.37
- 15. примерCramer's phi = 0.37 (φ2 = 0.137)
- 16. λ – лямбдаНоминальная-номинальная; Значение лямбды показывает, насколько
- 17. Скачать презентанцию
Типы переменных и гипотезыНезависимые переменные – Х1 и Х2Независимая переменная – ХЗависимая переменная – УГипотеза – научно-обоснованное предположение о направлении (и силе) отношения между Х1 и Х2 или Х и У
Слайды и текст этой презентации
Слайд 2Типы переменных и гипотезы
Независимые переменные – Х1 и Х2
Независимая переменная
– Х
(и силе) отношения между Х1 и Х2 или Х и УСлайд 3Ассоциация и причина
Одна переменная причина другой – необходимое и
достаточное условие:
если есть А, всегда происходит B
если нет А, никогда
не происходит BДве переменные связаны между собой, часто происходят вместе или изменяются:
в одном направлении – когда А увеличивается, увеличивается B
в противоположных направлениях – когда А увеличивается, B – уменьшается
Слайд 4Ассоциации и скрытые признаки
размер обуви и скорость чтения; продажи мороженного
и количество изнасилований; % обнаженных частей тела и количество купающихся
рост
и количество больничных; сексуальная активность и склонность к депрессииуспеваемость ребёнка связана с образованием родителей, образование родителей связано с их доходом, а доход родителей связан с их образованием…
потребление электроники и продолжительность жизни
Слайд 5Причинно-следственная связь: характеристики
Сила ассоциации (позволяет ли величина риска исключить другие
факторы)
Устойчивость (воспроизводимость результатов разными исследователями, в разных условиях)
Специфичность
(влияние связано с конкретным эффектом, а не широким спектром следствий) Необратимость (нет связи в обратном направлении)
Временной порядок (причина раньше следствия)
Правдоподобность (есть ли надёжные научные механизмы, объясняющие ассоциацию)
Экспериментальные данные (показывает ли физическое вмешательство результаты согласованные с наблюдаемой ассоциацией)
Аналогия (есть ли похожие результаты отношений между причиной и следствием, на которых мы можем построить аналогию)
Слайд 6Номинальная + номинальная
столбчатые диаграммы
таблицы сопряженности, анализ условных распределений
меры ассоциации: лямбда,
гамма, фи
экстраполяция: хи-квадрат
Слайд 7Номинальная + интервальная
бокс-плоты
равнение средних значений
мера ассоциации: эта
экстраполяция: t test
Слайд 11Статистическая значимость взаимосвязи
Значимость показывает вероятность (p-value) того, что наблюдаемое распределение
случайно
Если (p) > 0,05 – мы говорим о том, что
наблюдаемая между переменными взаимосвязь является результатом случайности, флуктуации значений, стечения обстоятельств и т.п. Мы не можем утверждать, что она существует и в генеральной совокупности.Если Sig. (p) < 0,05, то мы на 95% уверенны, что обнаруженная связь неслучайна, т.е. существует в генеральной совокупности (при условии правильно сделанной выборки)
Слайд 12Интерпретация (p) статистической значимости
p < 0.01 – p меньше,
чем 1 из 100:
если в генеральной совокупности между X и
У нет взаимосвязи, то обнаруженная нами связь по чистой случайности появилась бы в 1 выборке из каждых 100 p = 0.10 – p равно 10 из 100:
наблюдаемая нами связь между Х и У случилась бы в десяти выборках из 100 даже если в генеральной совокупности связь между Х и У = 0
p > 0.05 – p больше, чем 5 из 100:
если в генеральной совокупности нет связи между Х и У, то наблюдаемые нами результаты появились бы более, чем в 5 выборках из 100 по чистой случайности
Слайд 13Меры парной ассоциации
Сила - насколько сильно связаны два рассматриваемых
признака? И направление – прямо или обратно-пропорционально связаны признаки?
0
– нет связи, признаки независимы+1 – идеальная прямо пропорциональная связь или –1 – идеальная обратно пропорциональная связь
PRE меры показывают насколько знание Х улучшает наши прогнозы (предсказания) значений У
Интерпретация значений PRE коэффициентов:
ниже 0,1 – слабая связь
от 0,1 до 0,2 – умеренная связь
от 0,2 до 0,3 – умеренно сильная связь
0,3 и выше – сильная связь
Слайд 14Фи [Cramer’s phi]
Номинальная-номинальная;
Cramer's phi = 0.37 – корреляция, симметричная
φ2
(phi*phi = 0.137) – PRE (коэффициент детерминации)
Слайд 15пример
Cramer's phi = 0.37 (φ2 = 0.137) означает, что предпочтения
обуви студентов на 14% определяются их полом. А значит, 86%
разброса предпочтений остается без объяснения, есть и другие переменные, которые на это влияют.Слайд 16λ – лямбда
Номинальная-номинальная;
Значение лямбды показывает, насколько нам удалось бы
уменьшить ошибочность нашего предсказания, когда мы опирались бы на одну
переменную, чтобы предсказать другую.Просто *100 и говорим в %;












![Взаимосвязи между двумя переменными Фи [Cramer’s phi]Номинальная-номинальная; Cramer's phi = 0.37 – корреляция, симметричнаяφ2 (phi*phi Фи [Cramer’s phi]Номинальная-номинальная; Cramer's phi = 0.37 – корреляция, симметричнаяφ2 (phi*phi = 0.137) – PRE (коэффициент детерминации)](/img/tmb/2/158190/206fa0c8c713fb81f2f72702155da140-800x.jpg)





















