Явление электромагнитной индукции

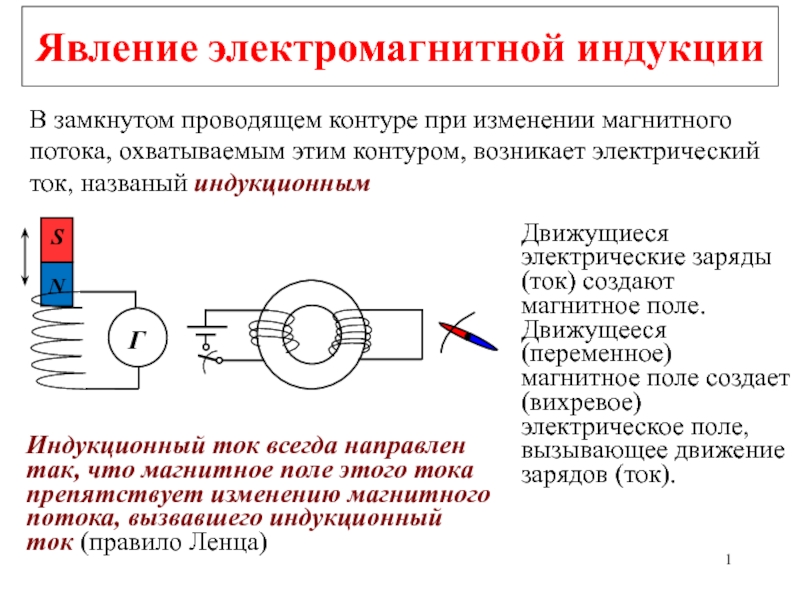
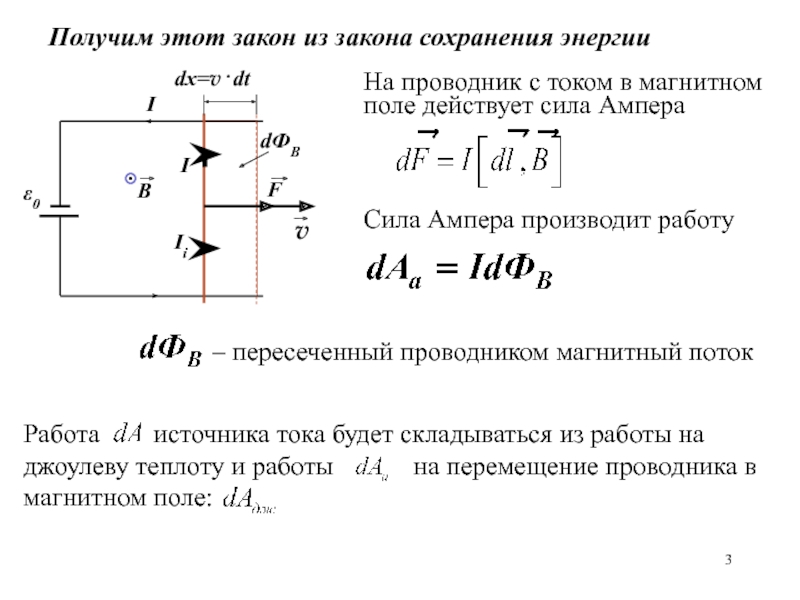
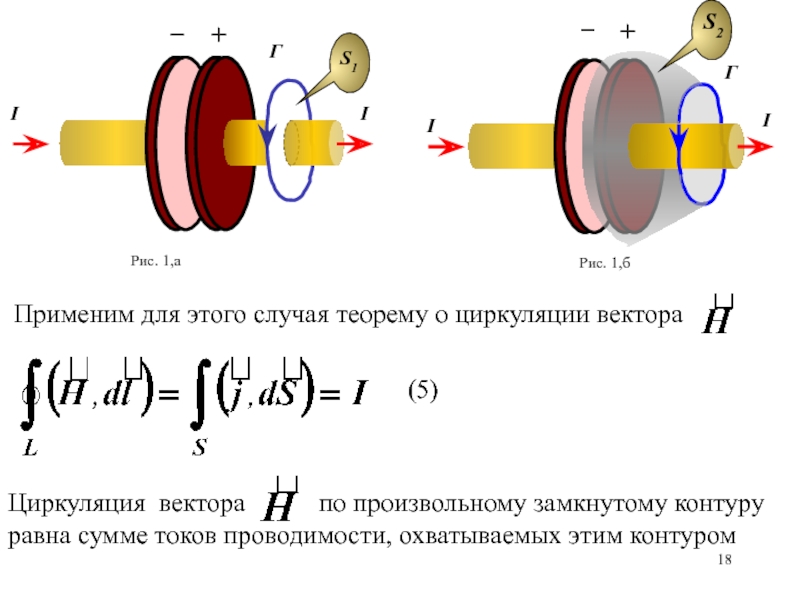
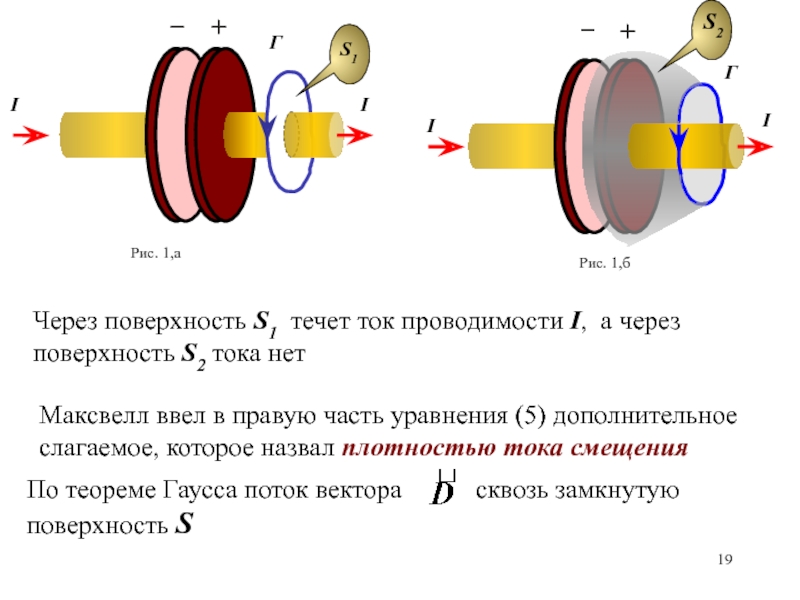
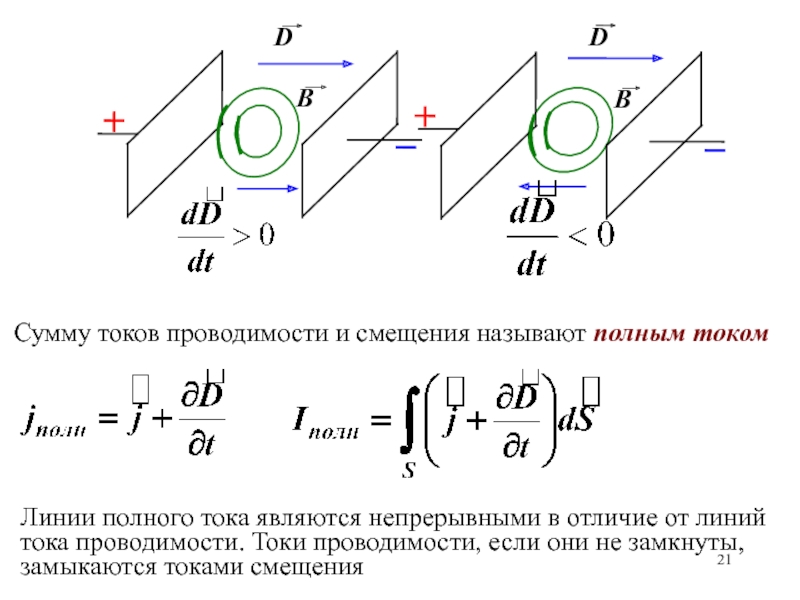
охватываемым этим контуром, возникает электрический ток, названый индукционным
Движущиеся электрические

Индукционный ток всегда направлен так, что магнитное поле этого тока препятствует изменению магнитного потока, вызвавшего индукционный ток (правило Ленца)

скоростью изменения магнитного потока ФВ
Какова бы ни была причина изменения

Э.д.с. электромагнитной индукции в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром.

Величина (модуль) э.д.с. индукции i не зависит от способа изменения магнитного потока

током в магнитном поле действует сила Ампера
Сила Ампера производит

– пересеченный проводником магнитный поток

Работа источника тока будет складываться из работы на джоулеву теплоту и работы на перемещение проводника в магнитном поле:

Разделим обе части на Idt
– есть закон Фарадея
Индукционный

Э.д.с. индуцируется в каждом витке. Полная э.д.с. i складывается из

(пси) потокосцепление или полный магнитный поток

Если магнитный поток, охватываемый каждым витком, одинаков и равен , то полный поток равен

в появлении индукционного тока, (ток появляется тогда, когда есть заряды

У вихревого электрического поля силовые линии замкнуты

Введём вектор напряжённости вихревого электрического поля

Когда заряд движется в магнитном поле (тоже переменном) на него действует сила Лоренца



т.к. поле вихревое

сплошных массивных проводниках. Эти токи оказываются замкнутыми в толще проводника

Вихревые токи возникают и в проводах, по которым течет переменный ток

Это явление называется скин-эффектом или поверхностным эффектом

две ситуации: при изменении тока в контуре изменяется магнитный поток,

Коэффициент пропорциональности L называется индуктивностью контура

Единица индуктивности называется генри (Гн)

, если внутри контура нет ферромагнетиков, т.к.

Индуктивность зависит от геометрии контура, числа витков и площади витка контура

в контуре 2 индуцируется э.д.с.
На рисунке магнитное

При протекании в контуре 2 тока силой возникает сцепленный с контуром 1 поток

На рисунке магнитное поле

э.д.с.
Контуры 1 и 2 называются связанными, а явление возникновения ЭДС

Коэффициенты пропорциональности и называются взаимной индуктивностью контуров

Единицы измерения (Гн).

Для двух соленоидов, намотанных на один сердечник

магнитного поля. Рассмотрим соленоид.
V – объём соленоида

поля по замкнутому контуру
(1)
– проекция вектора

Поток вектора магнитной индукции через ограниченную контуром поверхность S

(2)

Вихревое электрическое поле

Переменное магнитное поле порождает вихревое электрическое поле

не равна нулю
Следовательно, электрическое поле

(3)

лампа будет вспыхивать
Максвелл предположил, что поскольку меняющееся во времени

Максвелл ввел в рассмотрение так называемый ток смещения

по произвольному замкнутому контуру равна

S2 тока нет
Максвелл ввел в правую часть уравнения (5)

По теореме Гаусса поток вектора сквозь замкнутую поверхность S

(8)
Направление плотности тока смещения определяется направлением производной вектора

тока являются непрерывными в отличие от линий тока проводимости. Токи

будет иметь вид
(10)
По существу ток смещения –

Переменное электрическое поле вызывает появление магнитного поля. Взаимно порождаясь, они

Уравнения Максвелла в интегральной форме.

1.

равна со знаком минус производной по времени от магнитного потока

Это уравнение описывает явление электромагнитной индукции

В первом уравнении Максвелла

2.

Поток вектора индукции магнитного поля через произвольную замкнутую поверхность равен нулю.

Линии вектора магнитной индукции всегда замкнуты, и что магнитных зарядов нет. Это теорема Гаусса для поля

3.

равна полному току через произвольную поверхность, ограниченную этим контуром.
Показывает связь

4.

Поток вектора электрического смещения через произвольную замкнутую поверхность в произвольной среде равен стороннему заряду, заключенному внутри поверхности.

Это уравнение показывает, что силовые линии векторов начинаются или заканчиваются на зарядах.

Это теорема Гаусса для векторов

Для стационарных полей

и

между ними существует связь
5.
6.
7.
Уравнения (1 –

(набла):
Сам по себе этот оператор смысла не имеет.
Если умножить этот

Если вектор умножить скалярно на вектор , получится скаляр, который имеет смысл дивергенции вектора

векторно , получится

по произвольному замкнутому контуру

теоремой Остроградского–Гаусса

содержат уравнение непрерывности, выражающее закон сохранения электрического заряда.
3. Уравнения

4. Уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это обусловлено тем, что в природе существуют электрические заряды, но не обнаружены магнитные.

5. Из уравнений Максвелла следует, что электромагнитное поле способно существовать самостоятельно – без электрических зарядов и токов. Изменение состояния этого поля имеет волновой характер. Поля такого рода называют электромагнитными волнами