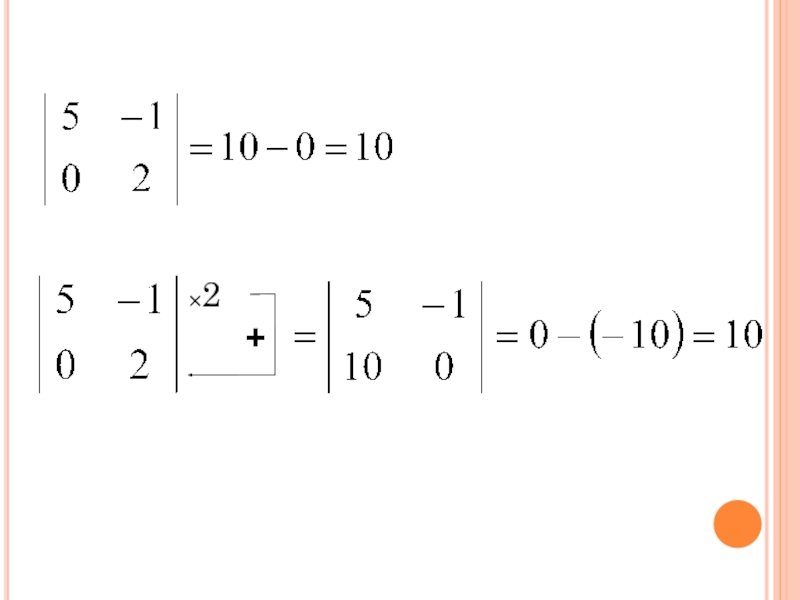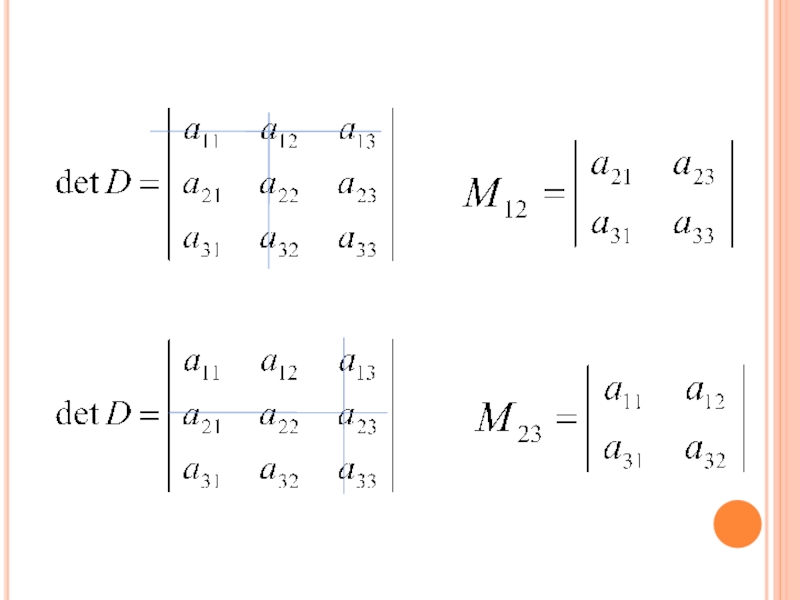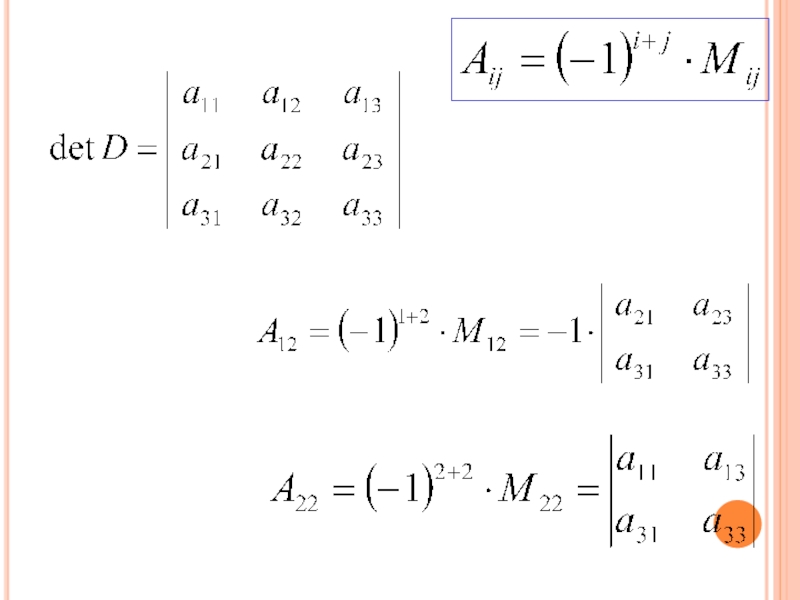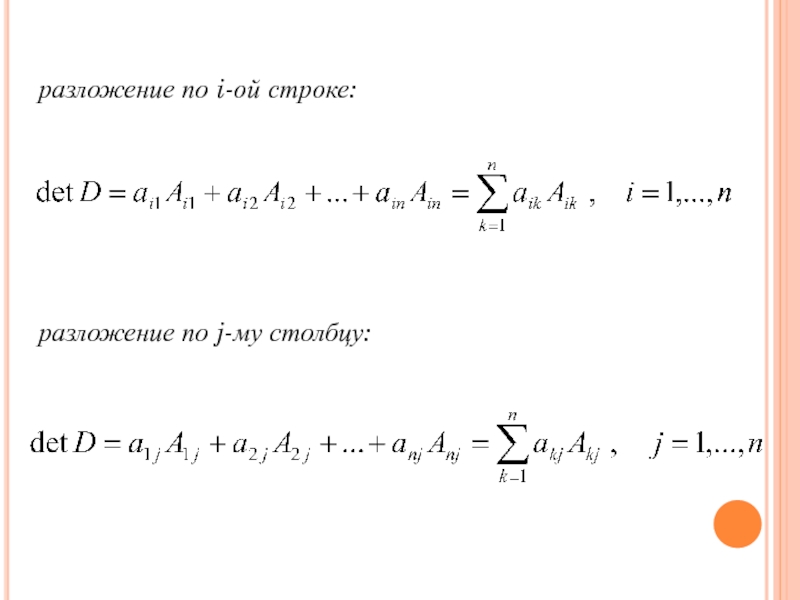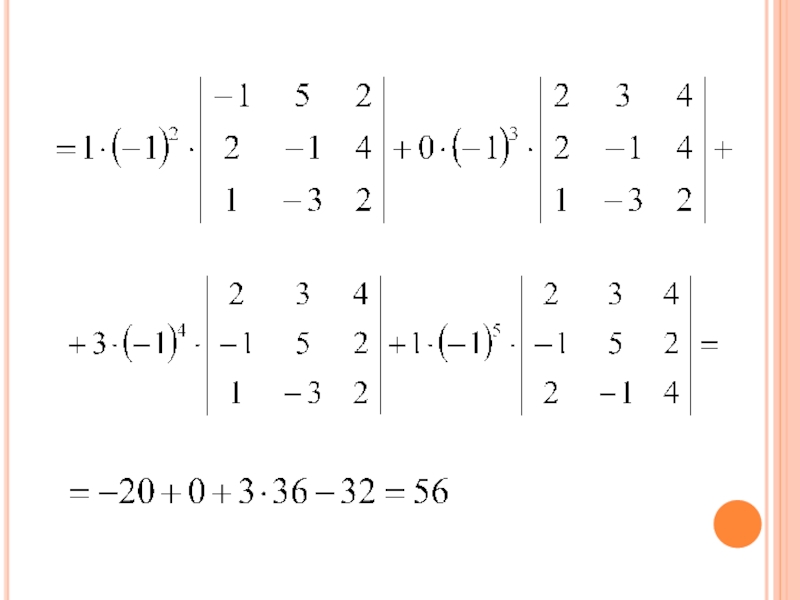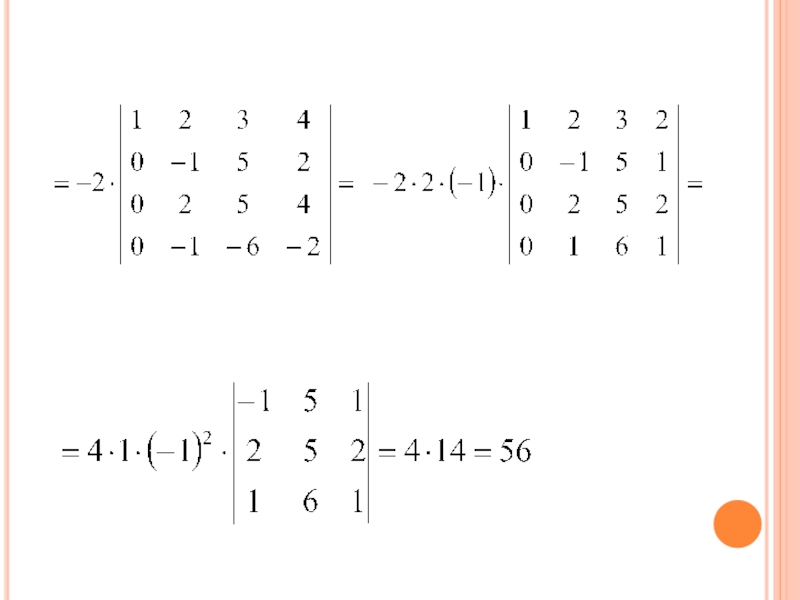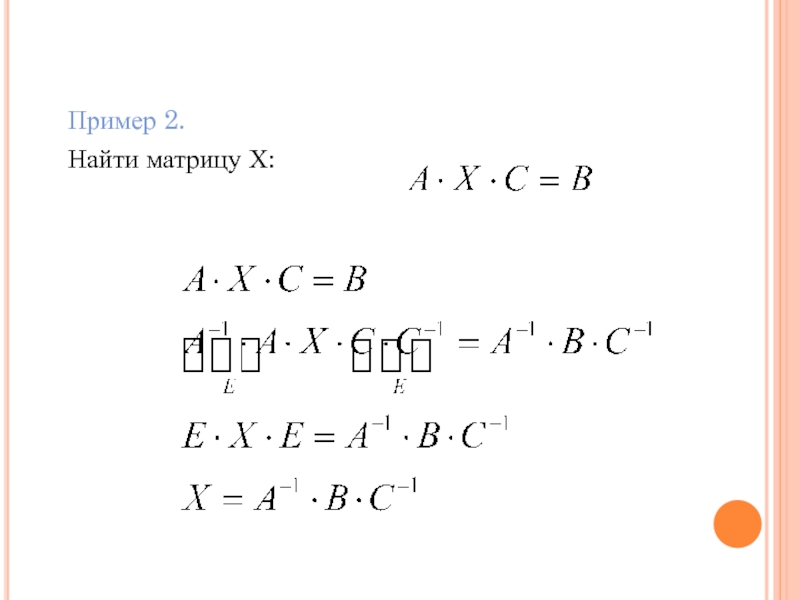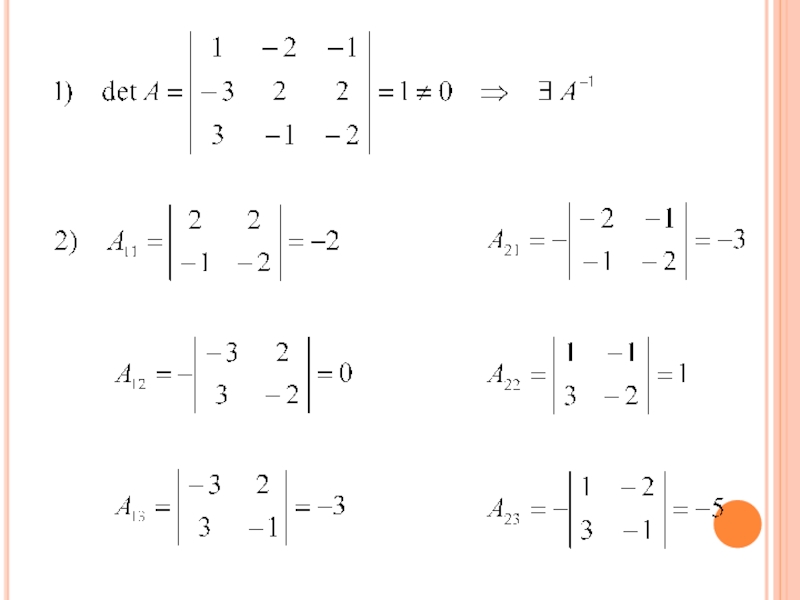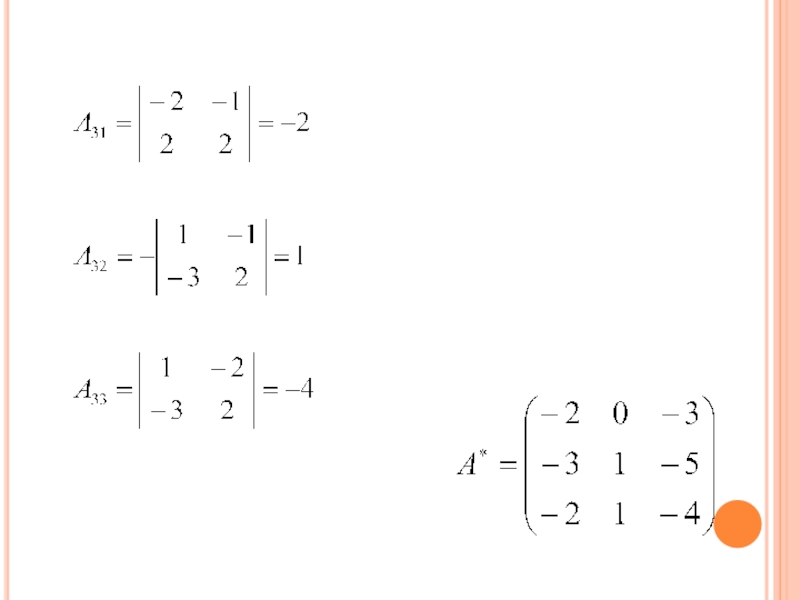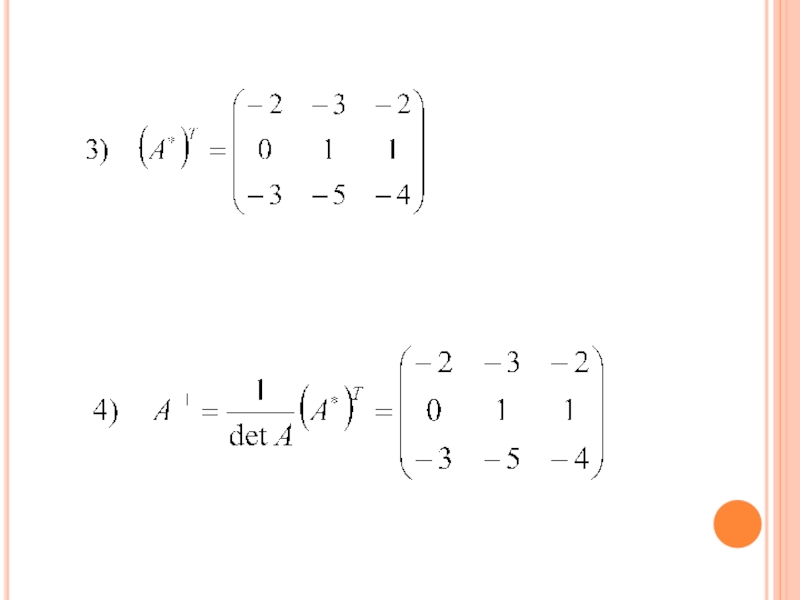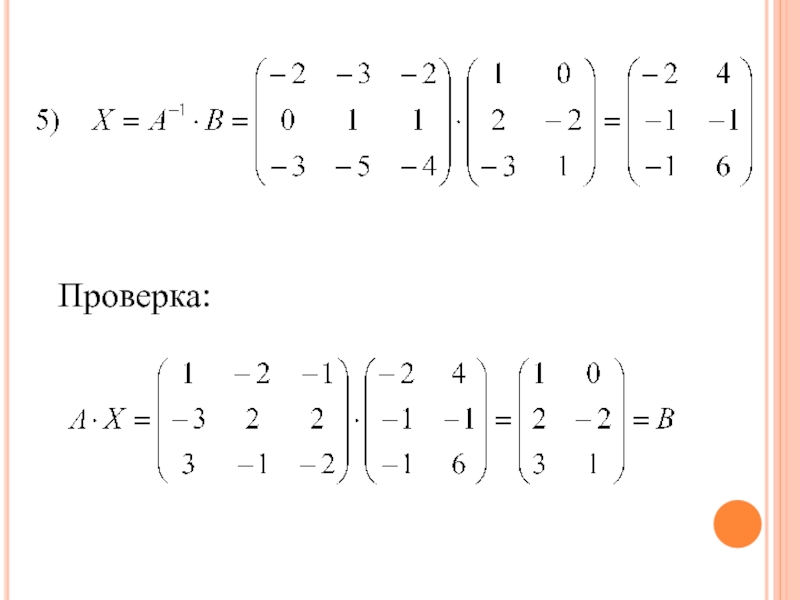Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ЮЖНО-УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ГУМАНИТАРНО-ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ Матрицы и
Содержание
- 1. ЮЖНО-УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ГУМАНИТАРНО-ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ Матрицы и
- 2. Раздел 1. Линейная алгебра.Линейная алгебра является
- 3. Тема 1. Матрицы Понятие матрицы и основанный
- 4. Матрицу А называют матрицей размера
- 5. Виды матрицЕсли количество строк равно количеству столбцов,
- 6. Квадратная матрица называется диагональной, если все элементы,
- 7. Квадратная матрица называется треугольной, если все элементы,
- 8. Матрица, содержащая один столбец или одну строку,
- 9. Матрица, полученная из данной заменой каждой ее
- 10. Действия над матрицамиОперация сложения матриц вводится только
- 11. Пример сложения и вычитания матрицДаны матрицы: Сумма матриц: Разность матриц:
- 12. Умножение на числоПроизведением матрицы
- 13. Операции сложения, вычитания и умножения матрицы на
- 14. Элементарные преобразования матрицЭлементарными преобразованиями матриц являются:
- 15. Пример: Привести к каноническому виду матрицуРешение: выполняя элементарные преобразования, получаем:
- 16. Произведение матрицПроизведением матрицы
- 17. Если матрицы А и В квадратные одного
- 18. Пример:
- 19. Если, конечно, написанные суммы и произведения матриц
- 20. Тема 2. ОпределителиКвадратной матрице А порядка n
- 21. Вычисление определителя 2-го порядка, иллюстрируется схемой:
- 22. Примеры:
- 23. При вычислении определителя 3-го порядка удобно пользоваться
- 24. Пример. Вычислить определитель третьего порядка =5•1•(-3) +
- 25. Пример. Вычислить определитель с помощью правила диагоналей-
- 26. 1. Определитель не изменится, если его транспонировать: Тема 2.2 Свойства определителей
- 27. 2. При перестановке двух строк или столбцов определитель изменит свой знак на противоположный.
- 28. 3. Определитель с двумя одинаковыми строками или столбцами равен нулю.
- 29. 4. Общий множитель всех элементов строки или столбца можно вынести за знак определителя.
- 30. Пример:
- 31. 5. Если все элементы двух строк (или столбцов) определителя пропорциональны, то определитель равен нулю.
- 32. 6. Если каждый элемент какого-либо ряда определителя
- 33. Слайд 33
- 34. 7. Если к какой-либо строке (или столбцу)
- 35. ×2+
- 36. 8. Треугольный определитель равен произведению элементов главной диагонали.
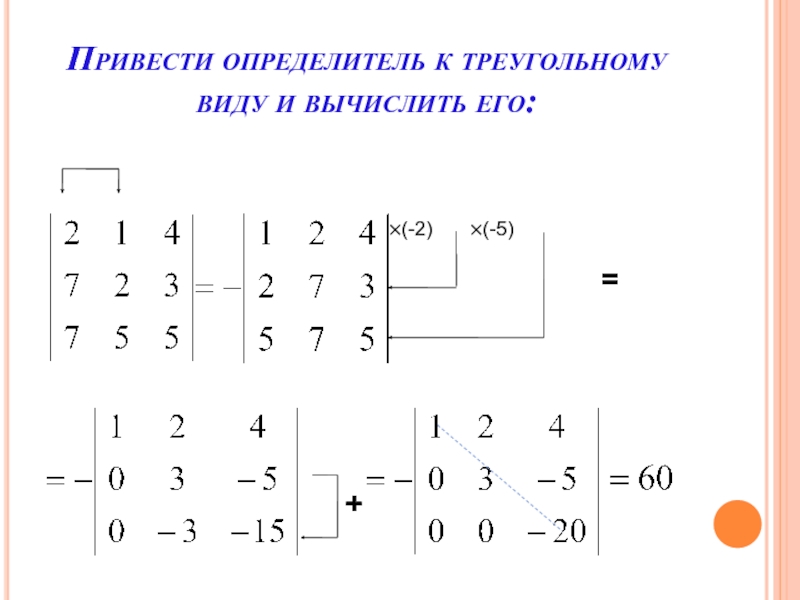
- 37. Привести определитель к треугольному виду и вычислить его:×(-2)×(-5)=+
- 38. Разложение определителя по элементам строки или столбца.Минором
- 39. Слайд 39
- 40. Алгебраическим дополнением Aij элемента aij det
- 41. Слайд 41
- 42. Сумма произведений элементов любой строки (или столбца)
- 43. разложение по i-ой строке: разложение по j-му столбцу:
- 44. Разложить данный определитель по элементам: 1) 3-ей строки; 2) 1-го столбца.
- 45. 1) Разложим данный определитель по элементам 3-ей строки:
- 46. Слайд 46
- 47. 2) Разложим данный определитель по элементам 1-го столбца:
- 48. Слайд 48
- 49. Основные методы вычисления определителя.1. разложение определителя по
- 50. Метод эффективного понижения порядка: Вычисление определителя n-го
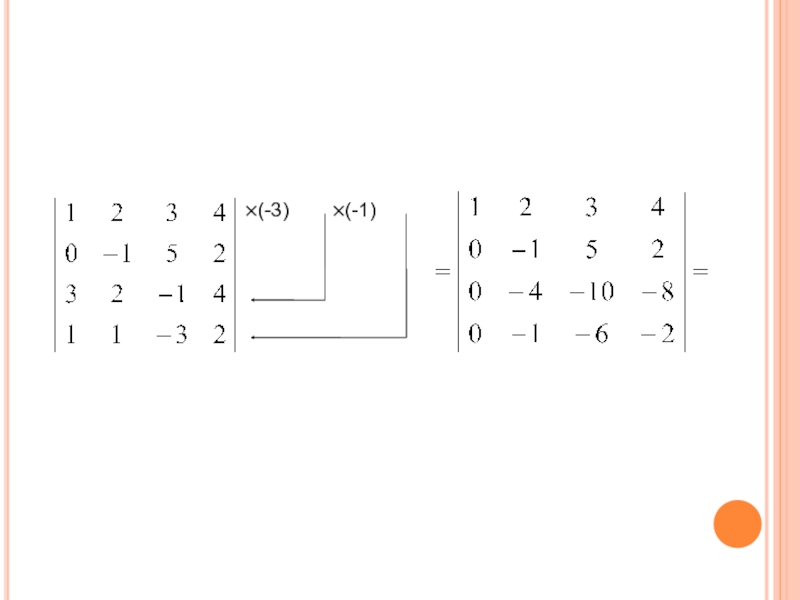
- 51. ×(-3)×(-1)
- 52. Слайд 52
- 53. Вычислить определитель приведением его к треугольному виду. ×(-3)×(-1)
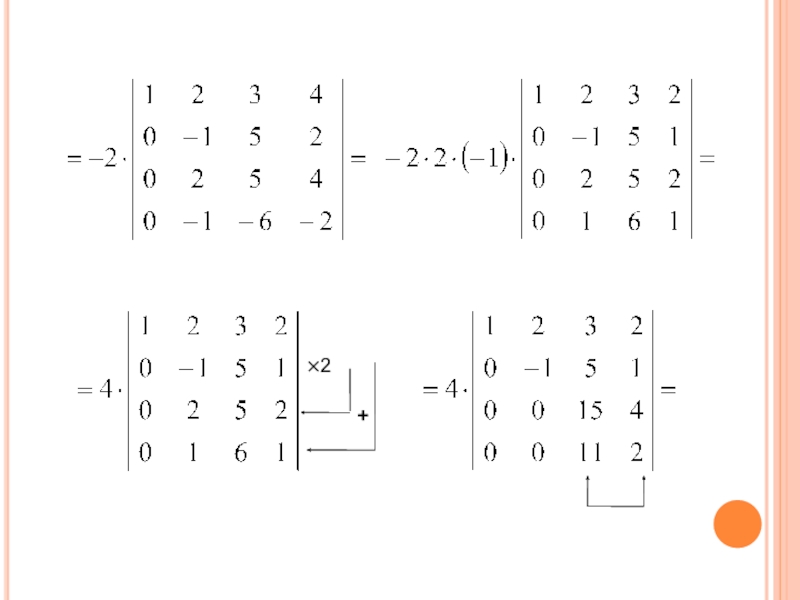
- 54. ×2+
- 55. ×(-2)
- 56. Тема 3. Обратная матрица
- 57. Квадратная матрица порядка n называется невырожденной,
- 58. Если А- квадратная матрица, то обратной по
- 59. Если обратная матрица существует, то матрица А
- 60. Теорема. Для того, чтобы квадратная матрица А имела
- 61. Нахождение обратной матрицы:где
- 62. Чтобы найти обратную матрицу:1. находят det A
- 63. Пример 1. Найти матрицу, обратную к матрице А:
- 64. 1) находим определитель матрицы А:
- 65. 2) находим алгебраические дополнения всех элементов матрицы А:
- 66. Слайд 66
- 67. записываем новую матрицу: 3) транспонируем эту матрицу:
- 68. 4) умножим полученную матрицу на
- 69. Проверка: Ответ:
- 70. Решение матричных уравнений.
- 71. Пример 2. Найти матрицу Х:
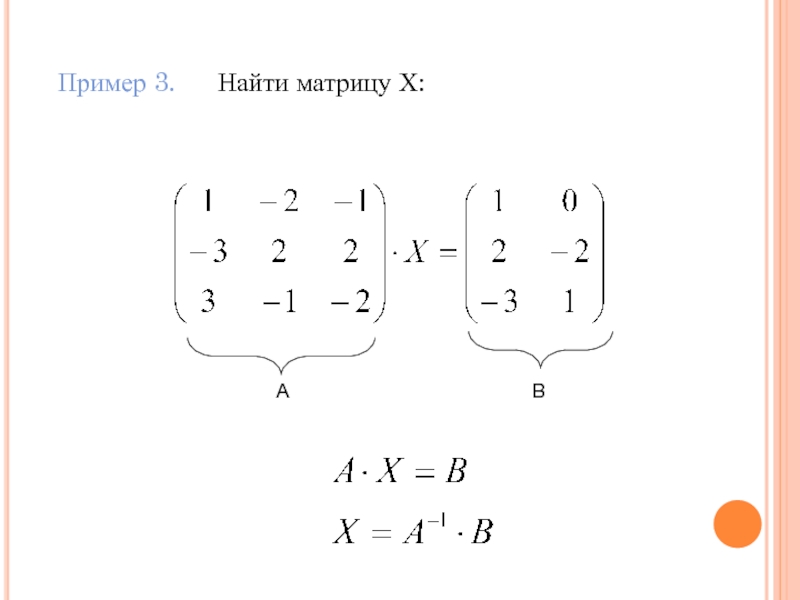
- 72. Пример 3. Найти матрицу Х: АВ
- 73. Слайд 73
- 74. Слайд 74
- 75. Слайд 75
- 76. Проверка:
- 77. Ответ:
- 78. Пример 4. Показать, что
- 79. Пусть Получили, что
- 80. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1ЮЖНО-УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ
ГУМАНИТАРНО-ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ
Матрицы и действия над ними
Челябинск, 2018
Слайд 2Раздел 1.
Линейная алгебра.
Линейная алгебра является необходимым инструментарием для компактного
и эффективного описания и анализа экономико-математических моделей и методов.
Слайд 3Тема 1. Матрицы
Понятие матрицы и основанный на нем раздел математики
– матричная алгебра – имеет важное значение для экономистов, так
как значительная часть математических моделей экономических объектов может быть записана в компактной матричной форме.Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины (или n столбцов одинаковой длины).
Матрица записывается следующим образом:
или где – элемент матрицы, i – ой строки и j – го
столбца,
где
i = 1,2…m
j = 1,2…n
Матрицы обозначаются прописными латинскими буквами.
Слайд 4Матрицу А называют матрицей размера и
пишут
Числа
, составляющие матрицу, называется ее элементами. Элементы, стоящие на диагонали, идущей из верхнего левого угла, образуют главную диагональ.Матрицы равны между собой, если равны все соответствующие элементы этих матриц, т.е.,
А=В, если , где
Слайд 5Виды матриц
Если количество строк равно количеству столбцов, т.е. m=n, то
матрица называется квадратной.
Квадратную матрицу размера n × n называют
матрицей n-го порядка.Если m = n, то матрица называется прямоугольной.
Слайд 6Квадратная матрица называется диагональной, если все элементы, не принадлежащие главной
диагонали, равны нулю.
Диагональная матрица, у которой все элементы главной
диагонали равны единице, называется единичной матрицей и обозначается символом Е.Слайд 7Квадратная матрица называется треугольной, если все элементы, расположенные по одну
сторону от главной диагонали, равны нулю.
Матрица, все элементы которой равны
нулю, называется нулевой. Обозначается буквой О. Имеет вид:В матричном исчислении матрицы О и Е играют роль чисел 0 и 1 в арифметике.
Слайд 8Матрица, содержащая один столбец или одну строку, называется вектором (или
вектор-столбец, или вектор-строка соответственно). Их вид:
Матрица размера 1 × 1,
состоящая из одного числа, отождествляется с этим числом, т.е. есть 5. Слайд 9Матрица, полученная из данной заменой каждой ее строки столбцом с
тем же номером, называется матрицей транспонированной к данной. Обозначается
.Так, если
Транспонированная матрица обладает следующим свойством: (АТ)Т = А.
Слайд 10Действия над матрицами
Операция сложения матриц вводится только для матриц одинаковых
размеров.
Суммой двух матриц
и называется матрица такая, чтоЗаписывают С=А+В.
Сложение
Все свойства сложения соответствуют вычитанию.
Вычитание
Слайд 12Умножение на число
Произведением матрицы
на число k называется матрица
такая, чтоЗаписывают B=kA.
Пример:
Матрица – А= (-1) А называется противоположной матрице А.
Слайд 13Операции сложения, вычитания и умножения матрицы на число обладают следующими
свойствами:
А + В = В + А (коммутативность)
А +
(В + С) = (А + В) + С – ассоциативность А + 0 = А
А – А = 0
1 А = А
(А + В) = А + В – дистрибутивность
( + ) А = А + А
(А) = () А
где А, В, С – матрицы, и – числа.
Слайд 14Элементарные преобразования матриц
Элементарными преобразованиями матриц являются:
перестановка местами двух
параллельных рядов матрицы;
умножение всех элементов ряда матрицы на число,
отличное от нуля;прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и тоже число.
Две матрицы называются А и В эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. Записывается А В.
При помощи элементарных преобразований любую матрицу можно привести к матрице, у которой в начале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны нулю. Такую матрицу называют канонической, например:
Слайд 15Пример: Привести к каноническому виду матрицу
Решение: выполняя элементарные преобразования, получаем:
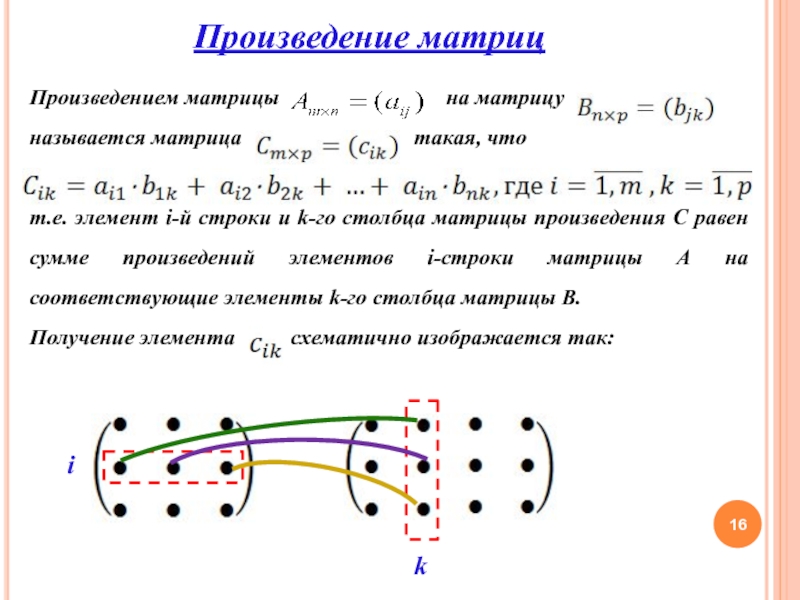
Слайд 16Произведение матриц
Произведением матрицы
на матрицу
называется матрица такая, чтот.е. элемент i-й строки и k-го столбца матрицы произведения С равен сумме произведений элементов i-строки матрицы А на соответствующие элементы k-го столбца матрицы В.
Получение элемента схематично изображается так:
i
k
Слайд 17Если матрицы А и В квадратные одного размера, то произведения
АВ и ВА всегда существуют. Легко показать, что А
Е = Е А=А, где А – квадратная матрица, Е – единичная матрица того же размера.Пример:
Слайд 18Пример:
.
Тогда произведение А В не определено, так как число столбцов матрицы А не совпадает с числом строк матрицы В. При этом определено произведение В × А, которое считают следующим образом:
Матрицы А и В называются перестановочными, если АВ = ВА. Умножение матриц обладает следующими свойствами:
А (В С) = (А В) С
А (В + С) = АВ + АС
(А + В) С = АС + ВС
(АВ) = (А)В
Слайд 19Если, конечно, написанные суммы и произведения матриц имеют смысл.
Для операции
транспонирования верны свойства:
(А + В)Т = АТ + ВТ
(АВ)Т =
ВТ АТСлайд 20Тема 2. Определители
Квадратной матрице А порядка n можно сопоставить число
det A (или А, или ), называемое
ее определителем, следующим образом:n = 1.
n = 2.
n = 3.
Определитель матрицы А также называют детерминантом.
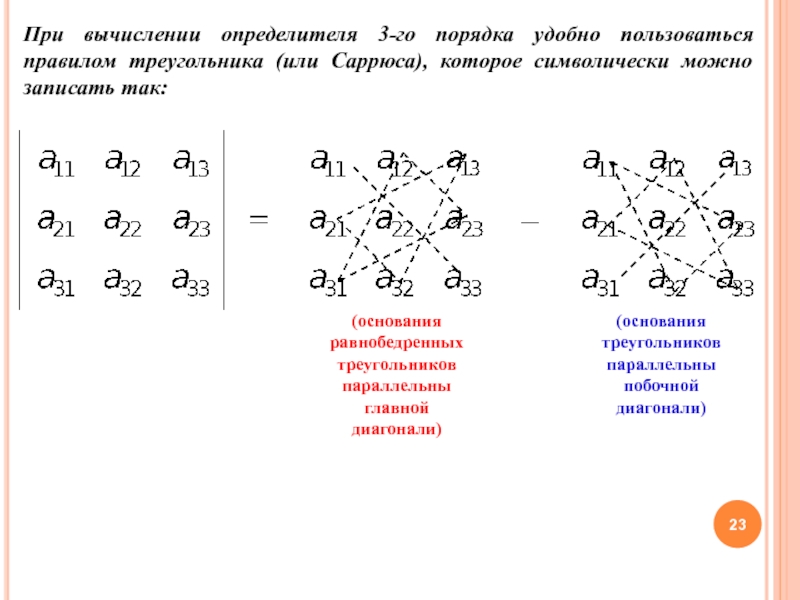
Слайд 23При вычислении определителя 3-го порядка удобно пользоваться правилом треугольника (или
Саррюса), которое символически можно записать так:
(основания равнобедренных треугольников параллельны
главной диагонали)(основания треугольников параллельны побочной диагонали)
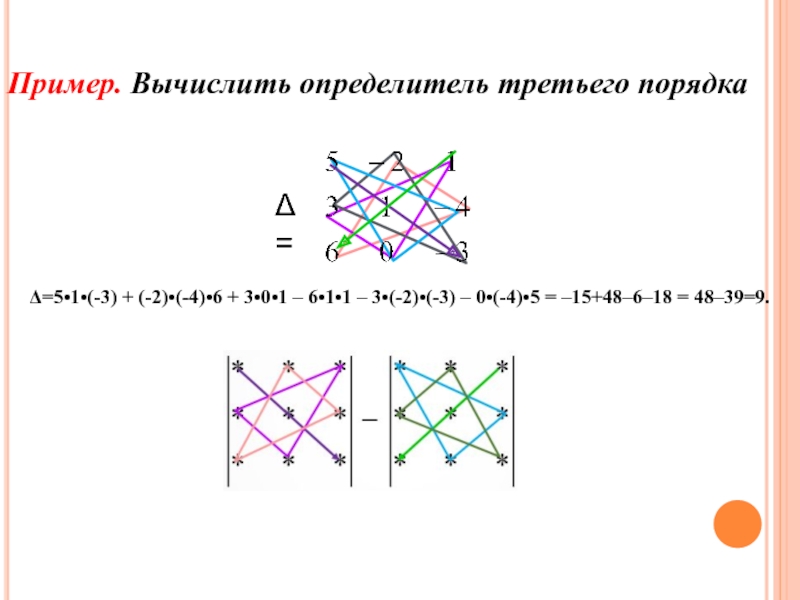
Слайд 24Пример. Вычислить определитель третьего порядка
=5•1•(-3) + (-2)•(-4)•6 + 3•0•1
– 6•1•1 – 3•(-2)•(-3) – 0•(-4)•5 = –15+48–6–18 = 48–39=9.
Слайд 25Пример. Вычислить определитель с помощью
правила диагоналей
- -
- + + +
=5•1•(-3) + (-2)•(-4)•6 + 3•0•1
– (6•1•1+ 0•(-4)•5+ 3•(-2)•(-3)) = = –15+48 – (6+18) = 33–24=9.=
Слайд 272. При перестановке двух строк или столбцов определитель изменит свой знак
на противоположный.
Слайд 315. Если все элементы двух строк (или столбцов) определителя пропорциональны,
то определитель равен нулю.
Слайд 326. Если каждый элемент какого-либо ряда определителя представляет собой сумму
двух слагаемых, то такой определитель равен сумме двух определителей, в
первом из которых соответствующий ряд состоит из первых слагаемых, а во втором- из вторых слагаемых.Слайд 347. Если к какой-либо строке (или столбцу) определителя прибавить соответствующие
элементы другой строки (или столбца) , умноженные на одно и
то же число, то определитель не изменится.×к
Слайд 38Разложение определителя по элементам строки или столбца.
Минором
элемента det D называется такой новый определитель, который
получается из данного вычеркиванием i-ой строки и j-го столбца содержащих данный элемент.Слайд 40 Алгебраическим дополнением Aij элемента aij det D называется минор
Mij этого элемента, взятый со знаком
т.е.
Слайд 42Сумма произведений элементов любой строки (или столбца) определителя на их
алгебраические дополнения равна этому определителю.
Теорема:
Слайд 49Основные методы вычисления определителя.
1. разложение определителя по элементам строки или
столбца;
2. метод эффективного понижения порядка;
3. приведение определителя к треугольному виду.
Слайд 50Метод эффективного понижения порядка:
Вычисление определителя n-го порядка сводится к
вычислению одного определителя (n-1)-го порядка, сделав в каком-либо ряду все
элементы, кроме одного, равными нулю.Слайд 57
Квадратная матрица порядка n называется невырожденной, если её определитель
не равен нулю.
В противном случае (detA=0) матрица А называется вырожденной.
Слайд 58Если А- квадратная матрица, то обратной по отношению к матрице
А называется матрица, которая будучи умноженной на А (как справа,
так и слева) даёт единичную матрицу.Слайд 59Если обратная матрица существует, то матрица А называется обратимой.
Операция вычисления
обратной матрицы при условии, что она существует, называется обращением матрицы.
Слайд 60 Теорема.
Для того, чтобы квадратная матрица А имела обратную, необходимо и
достаточно, чтобы матрица А была невырожденной (det А≠ 0).
Слайд 62Чтобы найти обратную матрицу:
1. находят det A и убеждаются, что
det A ≠ 0;
2. находят алгебраические дополнения всех элементов матрицы
А и записывают новую матрицу А*;3. транспонируют новую матрицу ;
4. умножают полученную матрицу на