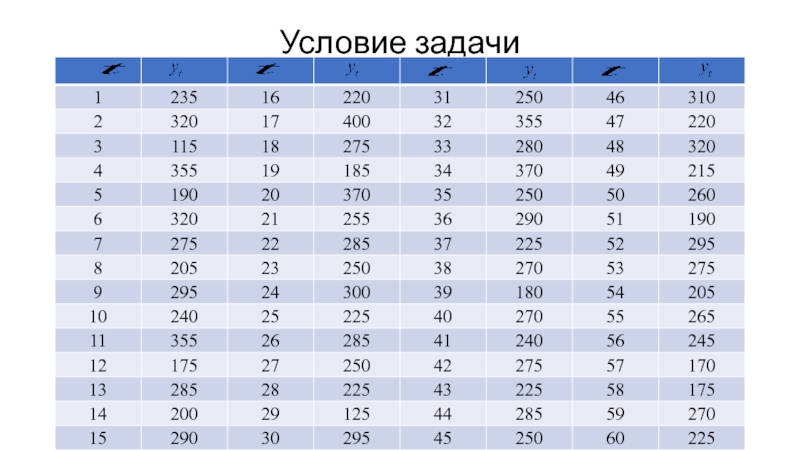
Слайд 3Имеются данные о размерах запасов компании А.
Требуется провести тестирование ряда
на постоянство математического ожидания и дисперсии с помощью параметрических тестов
на основе:
1. - критерия Стьюдента;
2. - критерия Фишера;
3. критерия Кокрена, основанного на распределении Фишер;
4. критерия Бартлетта.
и непараметрических тестов:
5. Манна-Уитни;
6. Сиджела – Тьюки;
Слайд 4Критерий Стьюдента
Для тестирования ряда на постоянство математического ожидания по критерию
Стьюдента, разобьем ряд на 2 части, в первую из которых
войдут наблюдения с 1 по 35, а во вторую – с 36 по 60.
Определим оценки математических ожиданий:
Слайд 5Критерий Стьюдента
Рассчитаем дисперсии:
Слайд 6Критерий Стьюдента
Сравнивая с критическим значением
приходим к выводу, что нельзя
отклонить гипотезу, что математическое ожидание постоянно, т.к.
Слайд 7Критерий Фишера
Проверка гипотезы о постоянстве дисперсии временного ряда в
случае разбиения исходного интервала на две части осуществляется с использованием
двухстороннего критерия Фишера. Расчетное значение критерия Фишера определяется:
Для нашего ряда:
Сравнивая его с табличным значением критерия Фишера с 34 и 24 степенями свободы:
можно сделать вывод, о том, что гипотеза о постоянстве дисперсии отвергается, так как
Слайд 8Критерий Кокрена
При разбиение ряда на несколько частей для проверки гипотезы
о постоянстве дисперсий может быть использован критерий Кокрена, основанный на
распределении Фишера. Он применяется в предположении, что объемы этих частей равны между собой. Расчетное значение этого критерия определяется:
А критическое значение критерия рассчитывается по формуле:
Слайд 9Критерий Кокрена
Где
и
Разобьем исходный ряд на
5 равных частей ( ).
Для каждой из подвыборок рассчитаем дисперсию по формуле:
Слайд 10Критерий Кокрена
Поскольку расчетное значение меньше критического значения, то нельзя отвергнуть
гипотезу о постоянстве дисперсии.
Слайд 11Критерий Бартлетта
В нашем примере разобьем ряд на 3 части: первая
– с 1 по 20, вторая – с 21 по
40, третья – 41 по 60. Рассчитаем дисперсии для подвыборок:
Общая дисперсия для всей выборки:
Слайд 12Критерий Бартлетта
Т.к.
, то значение критерия находится по формуле:
где
Слайд 13Критерий Бартлетта
получаем, при
так как
, нельзя отклонить гипотезу о постоянстве дисперсии.
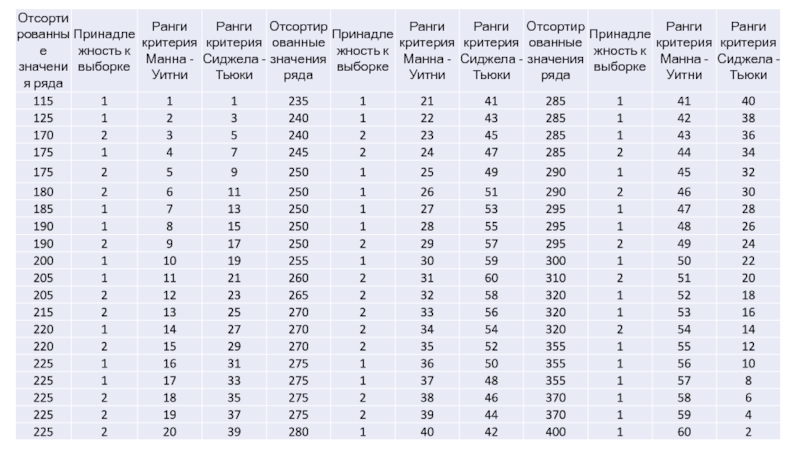
Слайд 15Критерий Манна - Уитни
Сумма рангов для первой подвыборке равна:
Тогда
стандартизованная переменная, рассчитанная по формуле:
Будет равна:
Слайд 16Критерий Манна - Уитни
Статистика Манна – Уитни имеет стандартное нормальное
распределение.
Так как ,
то гипотеза о постоянстве математического ожидания
принимается.
Слайд 17Критерий Cиджела - Тьюки
Сумма рангов критерия Сиджела –Тьюки для первой
подвыборки равна:
Тогда стандартизованная переменная, рассчитанная по формуле:
Будет равна:
Слайд 18Критерий Cиджела - Тьюки
Статистика Cиджела – Тьюки, так же как
и Манна - Уитни, имеет стандартное нормальное распределение.
И так
как ,
то гипотеза о постоянстве дисперсии не отклоняется.