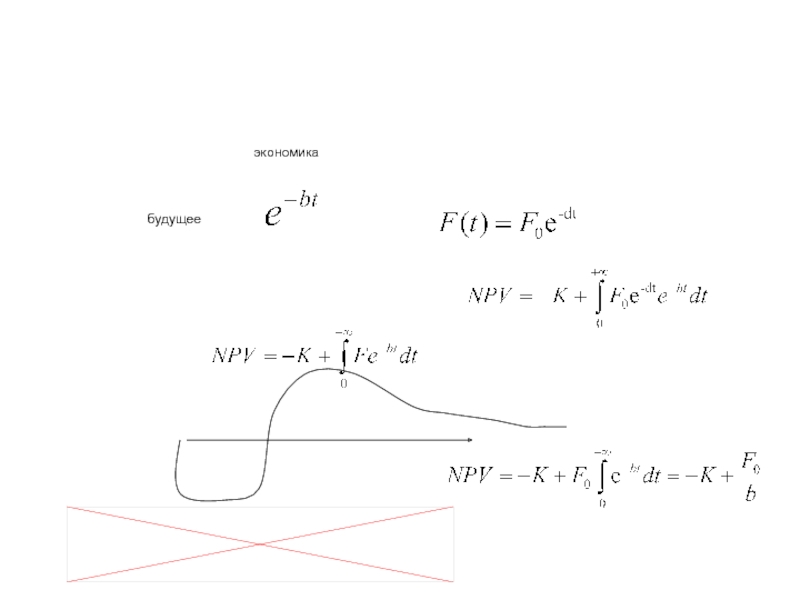
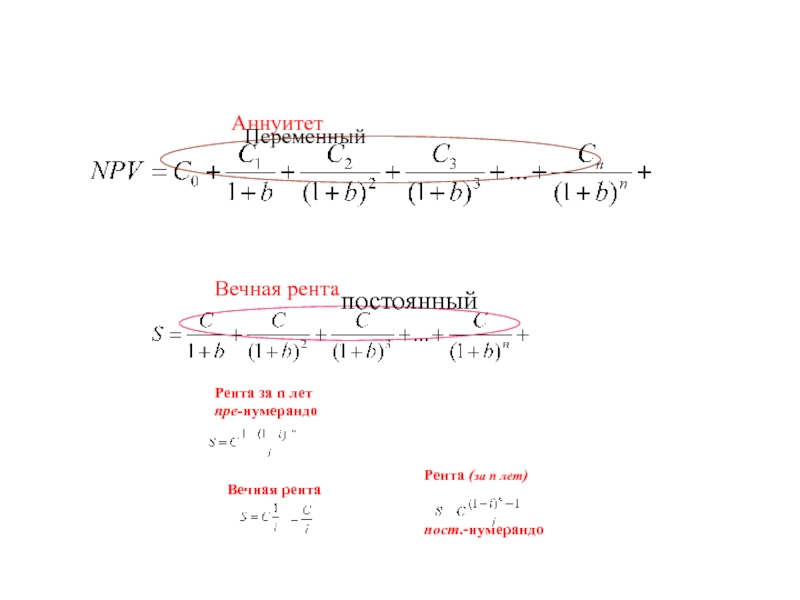
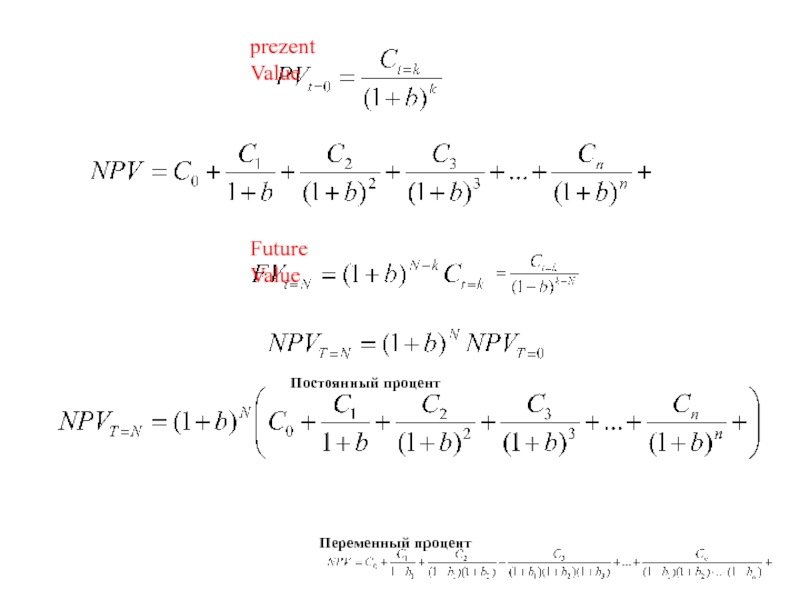
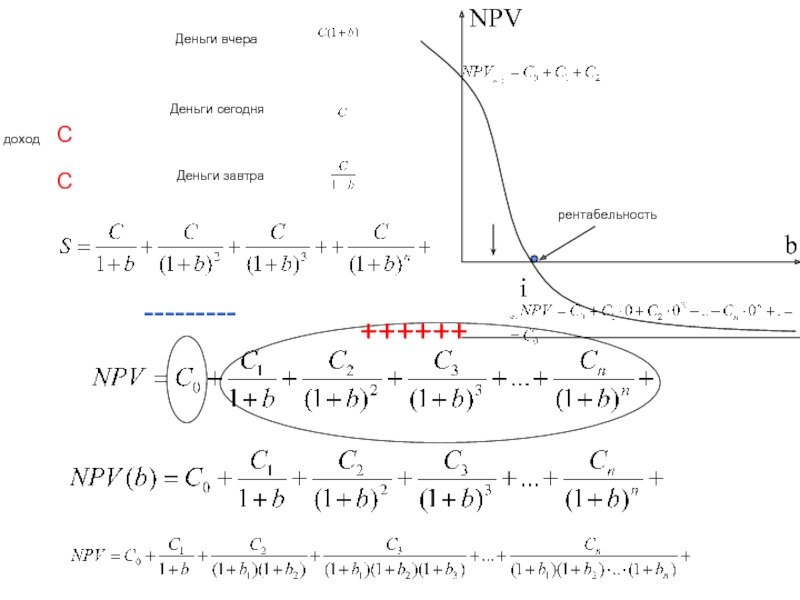
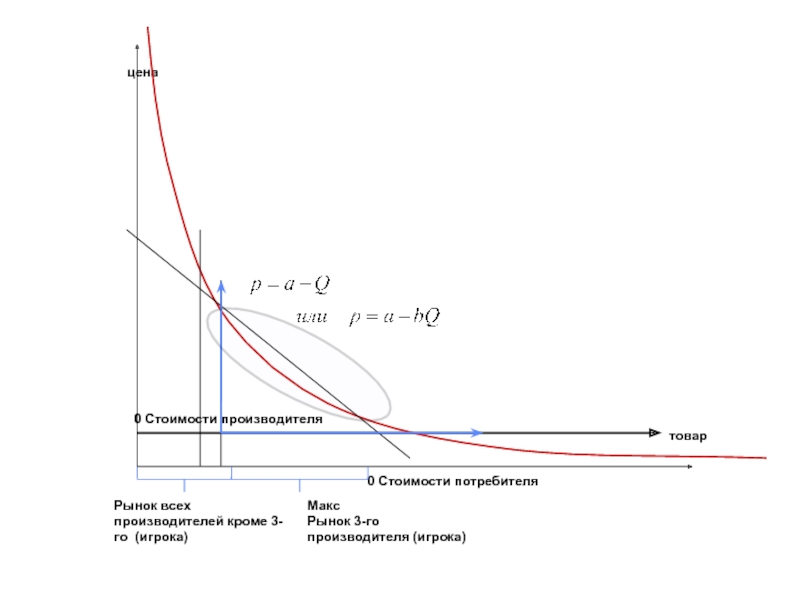
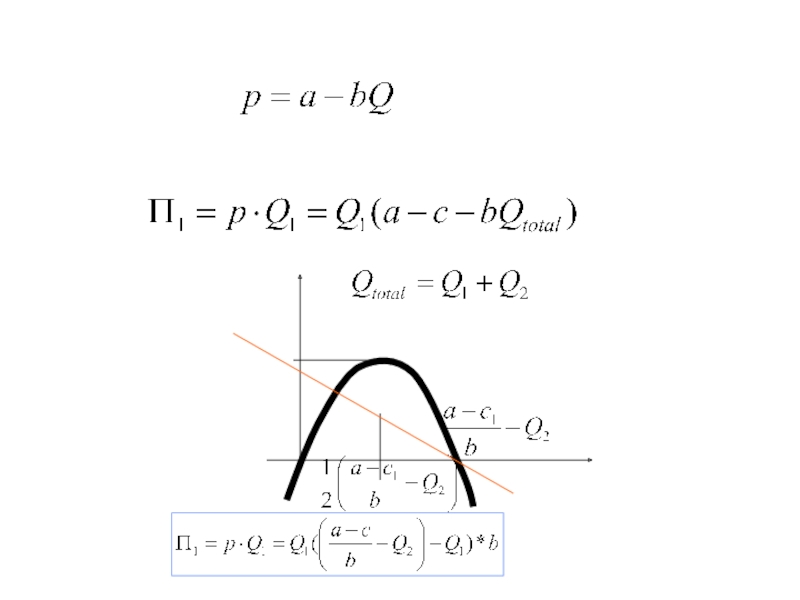
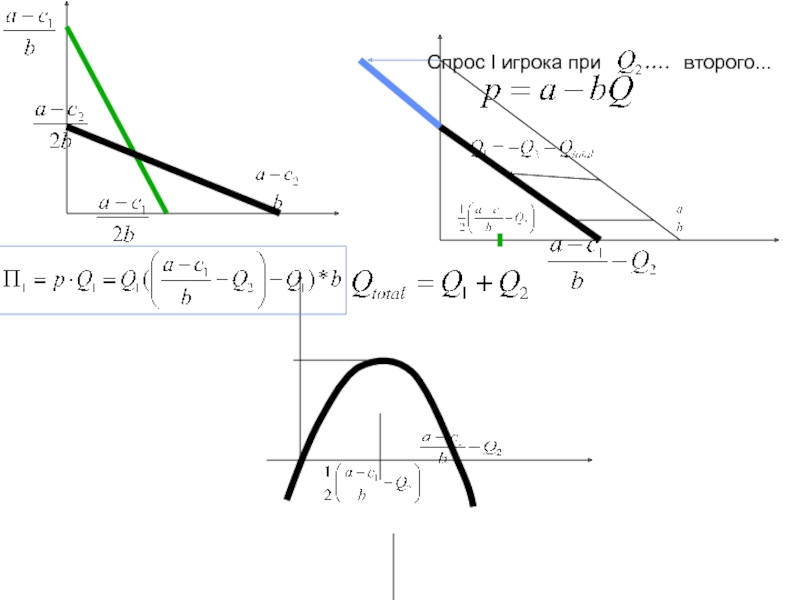
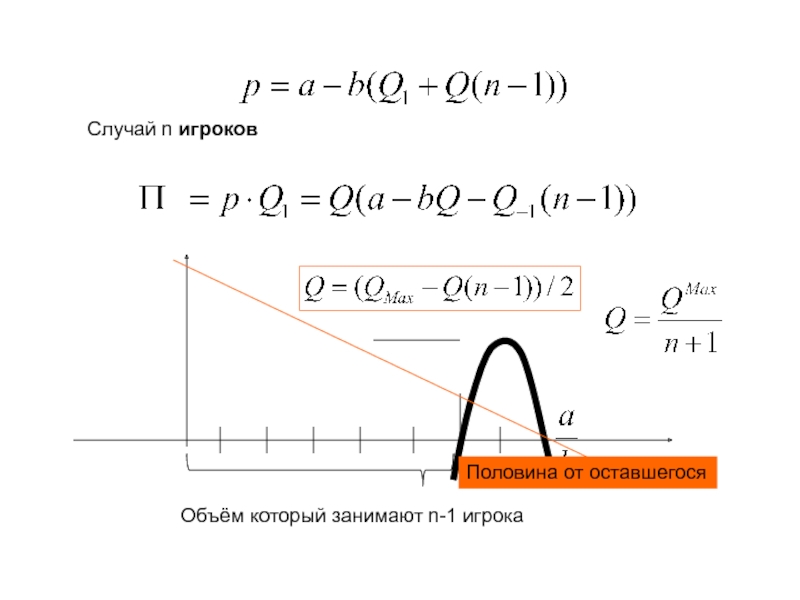
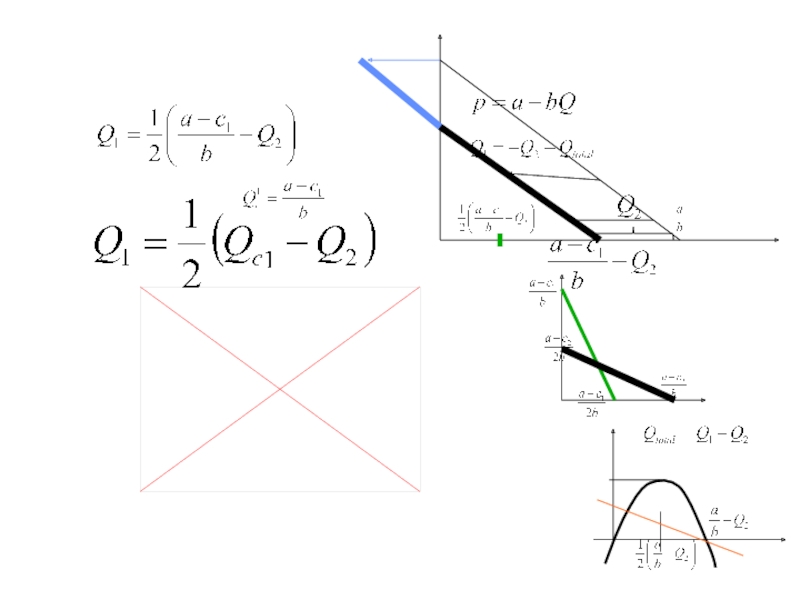
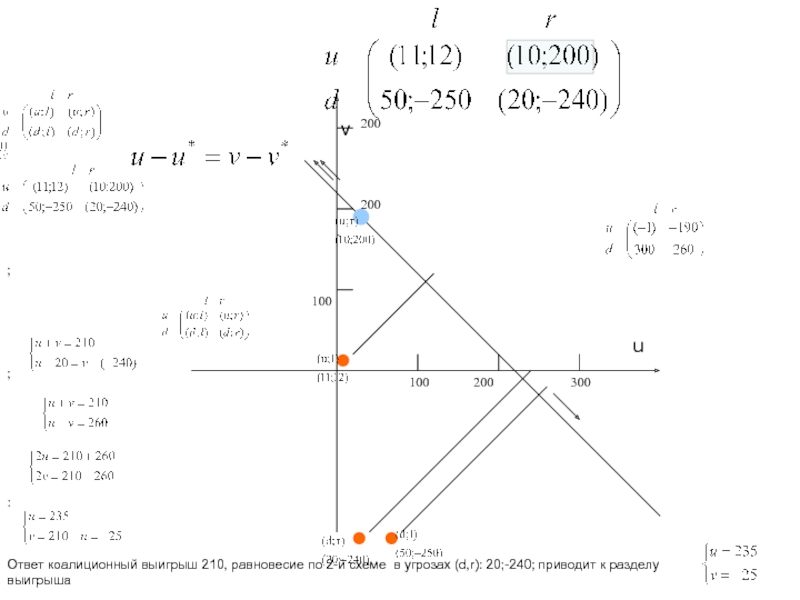
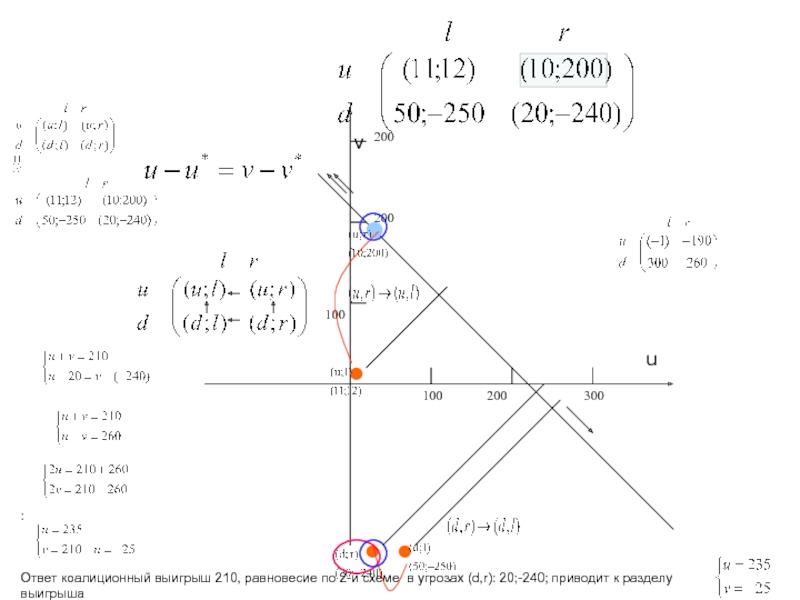
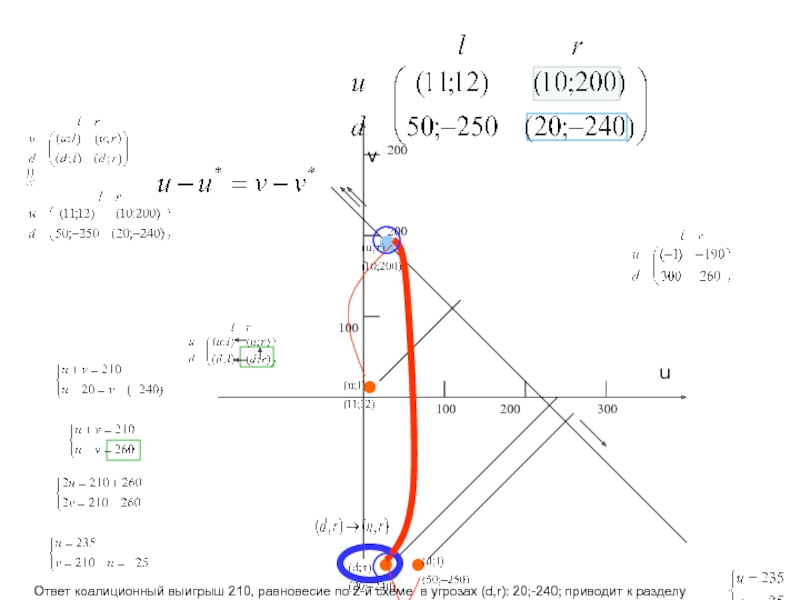
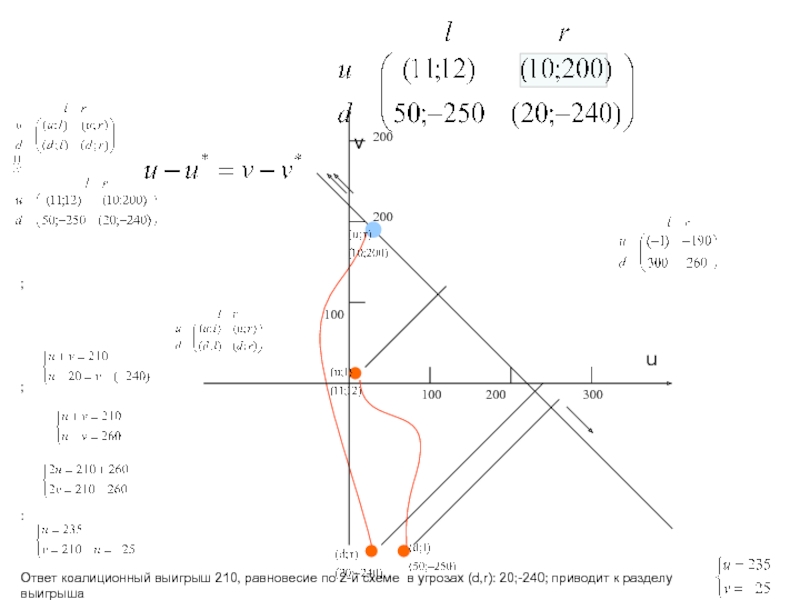
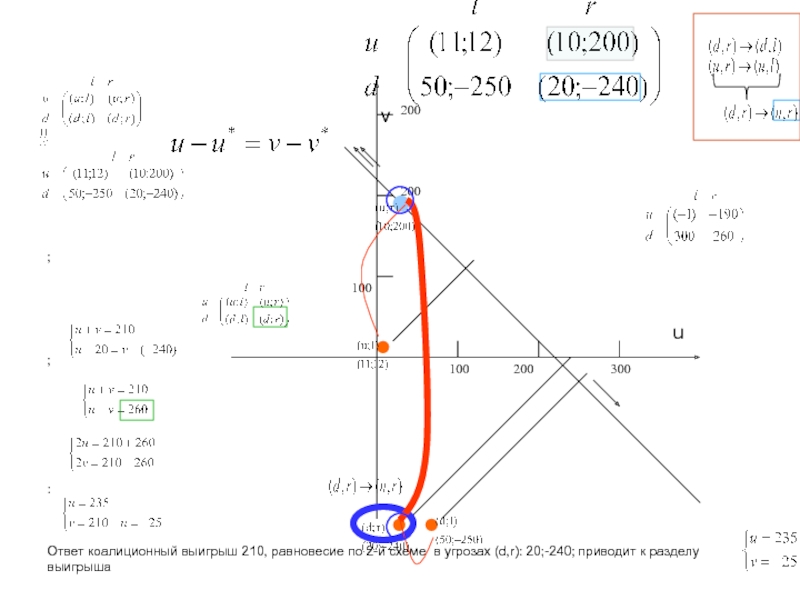
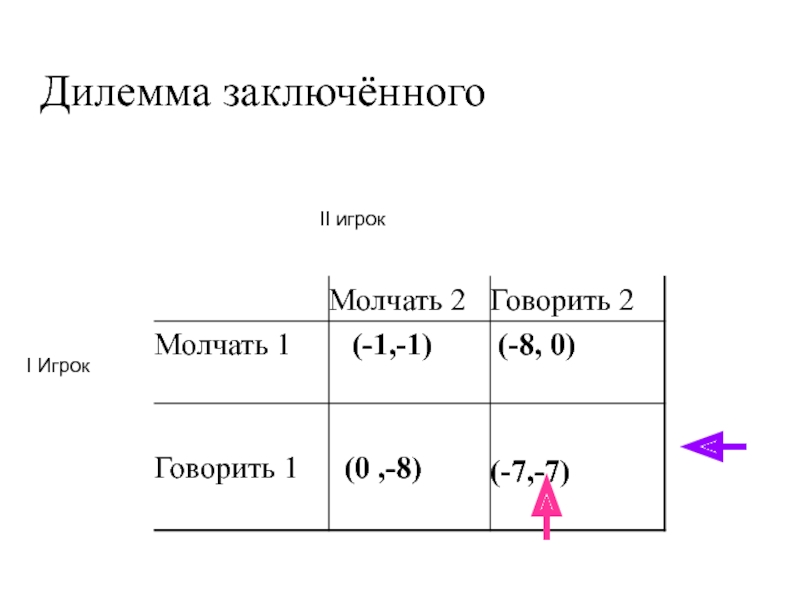
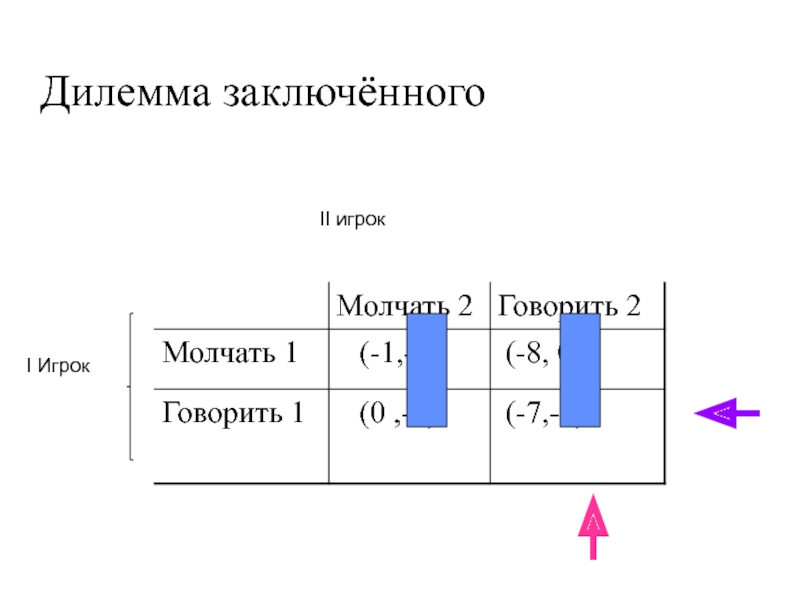
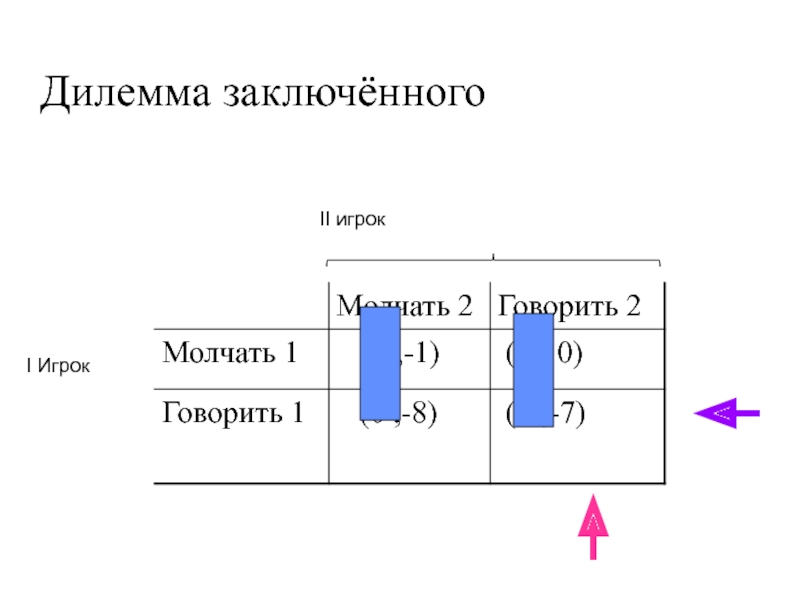
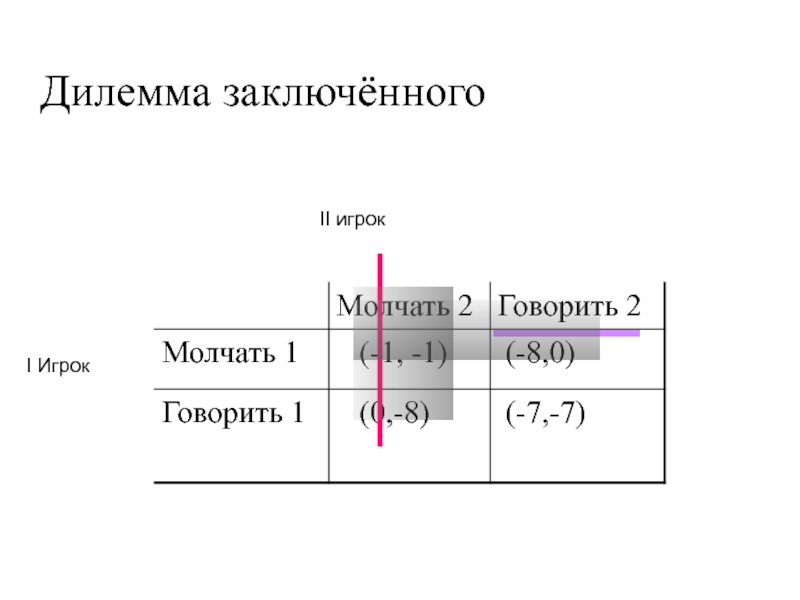
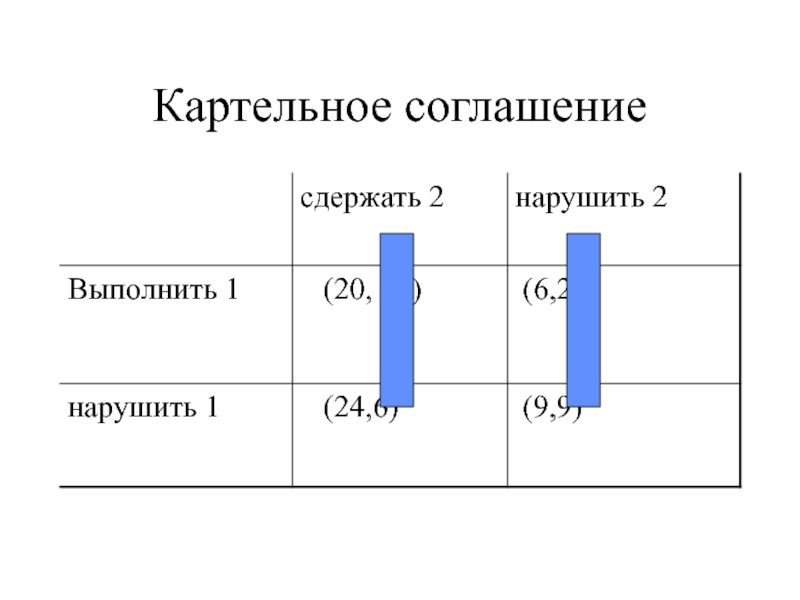
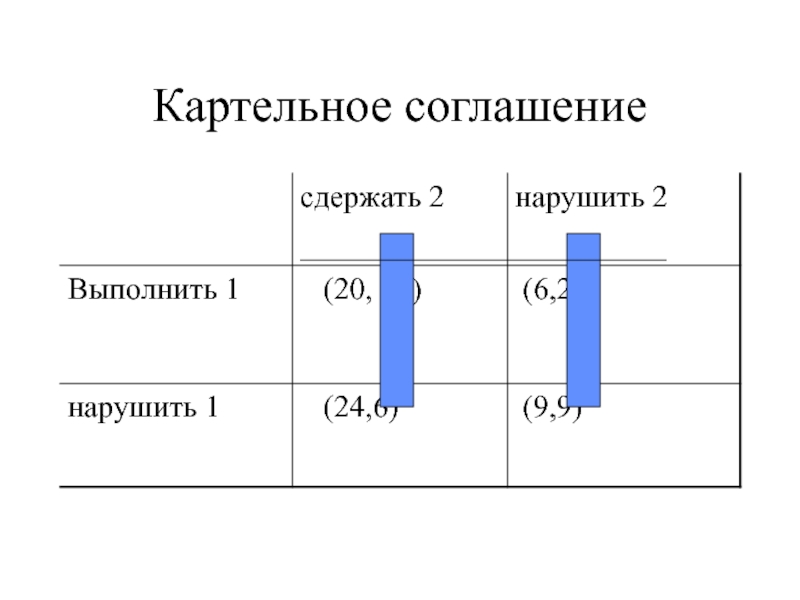
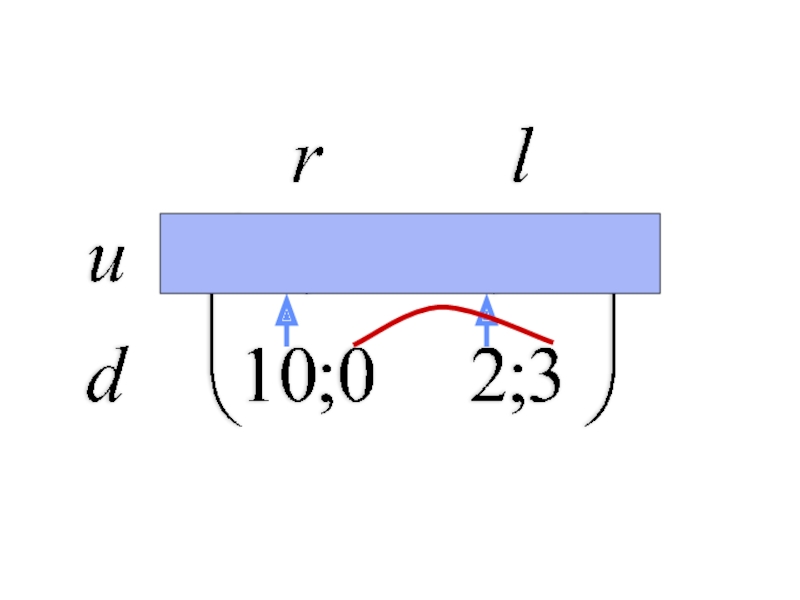
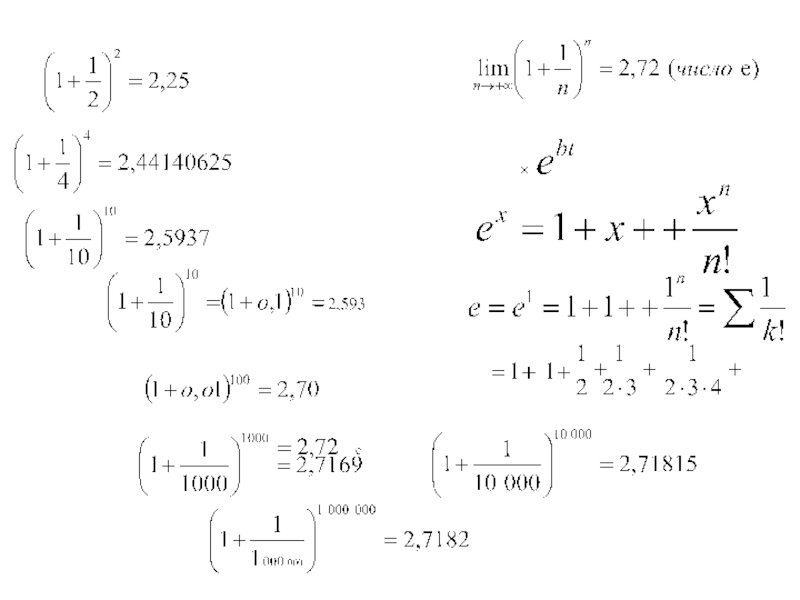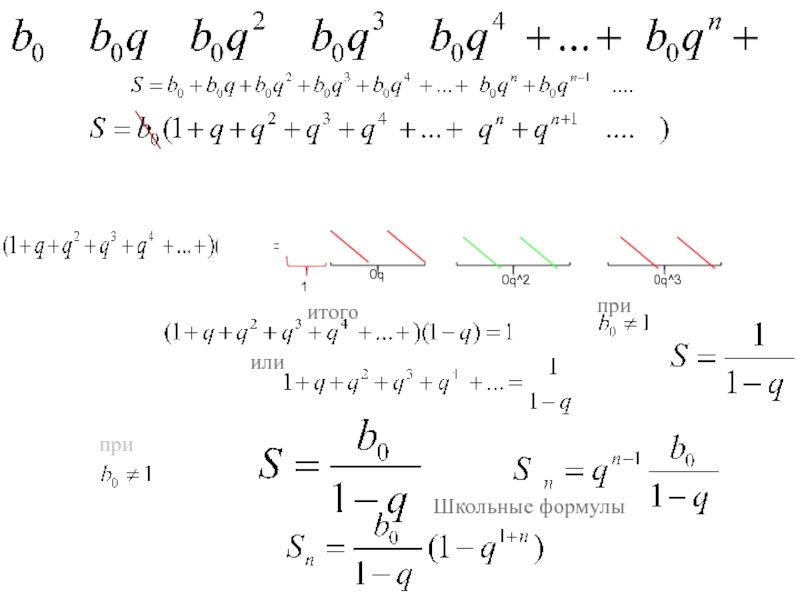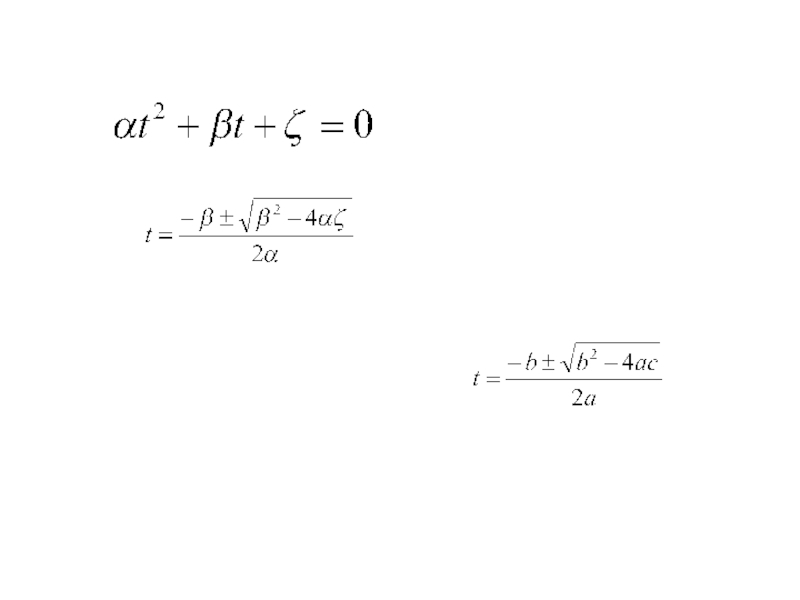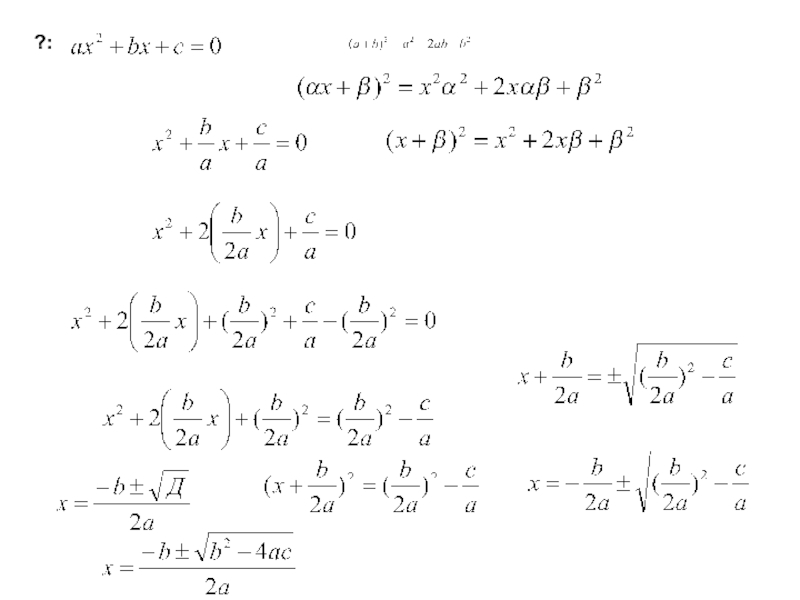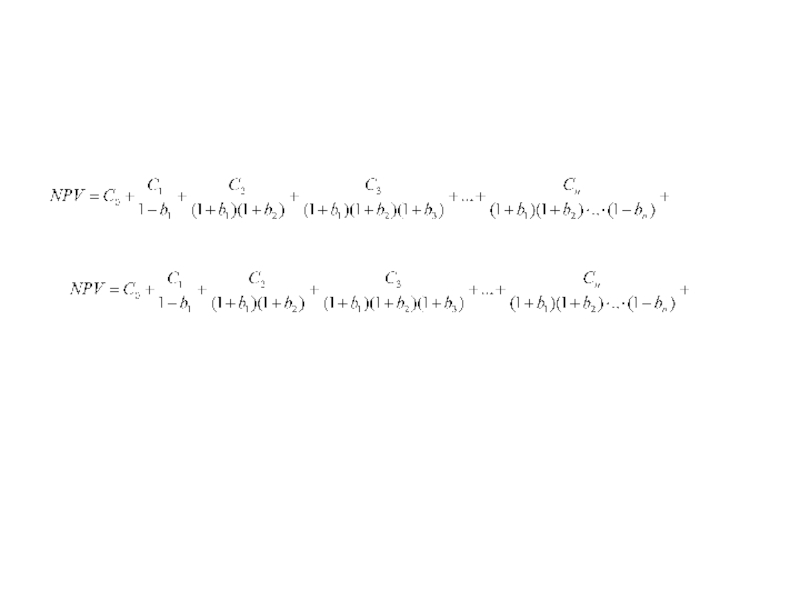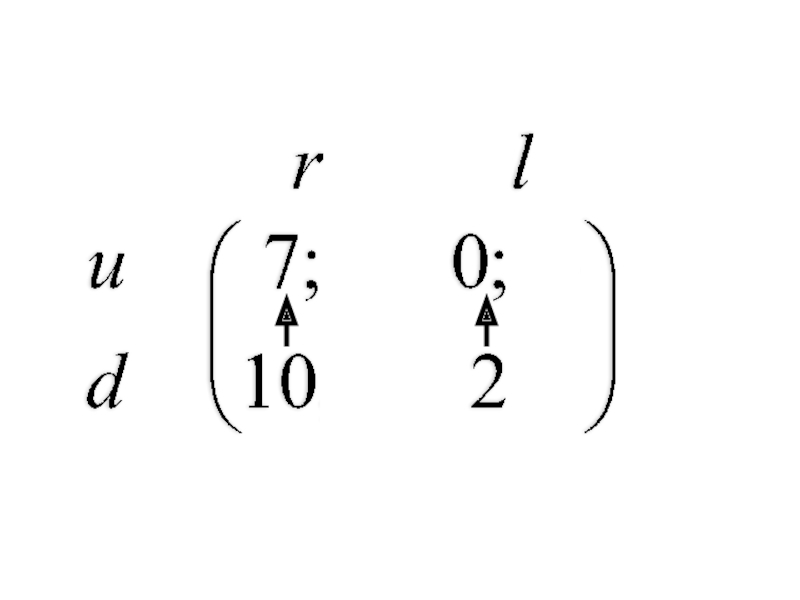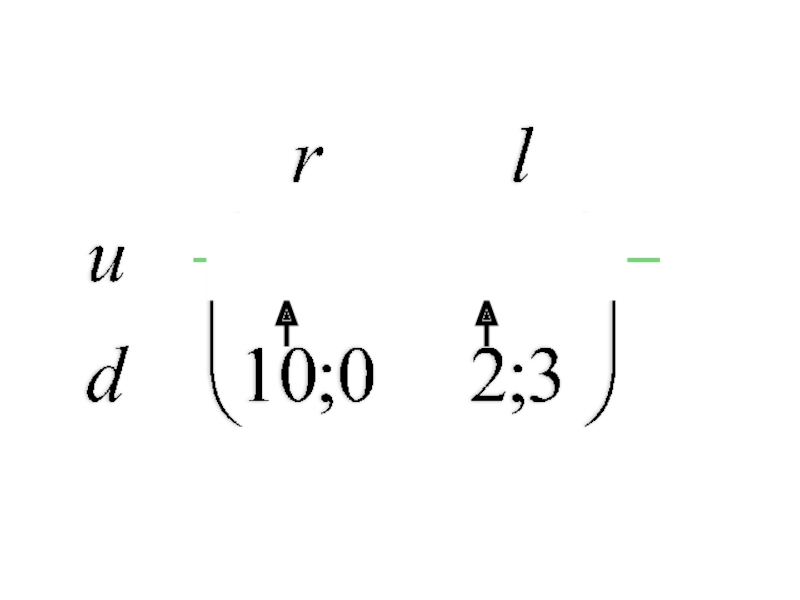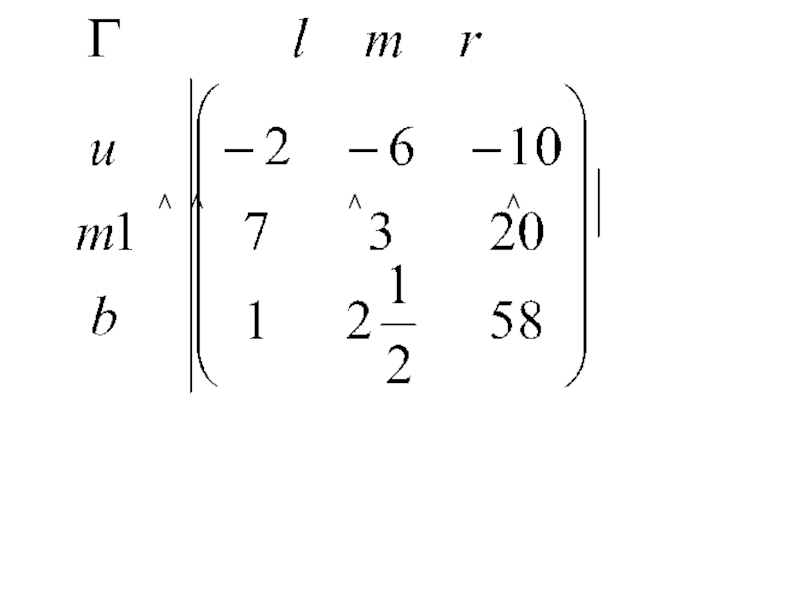ровно две отрасли).
Проверить выполнено ли достаточное условие продуктивности (вспомнить
признак апеллирующей к сумме элементов в строках).
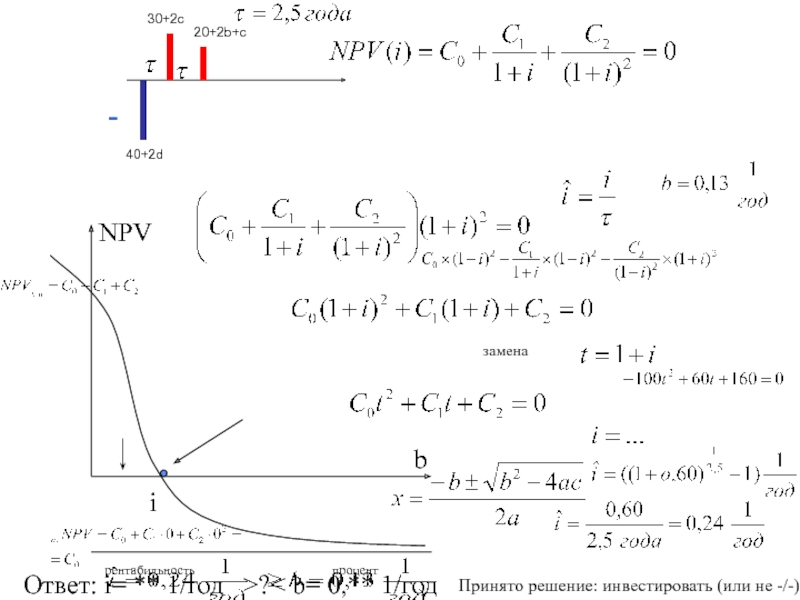
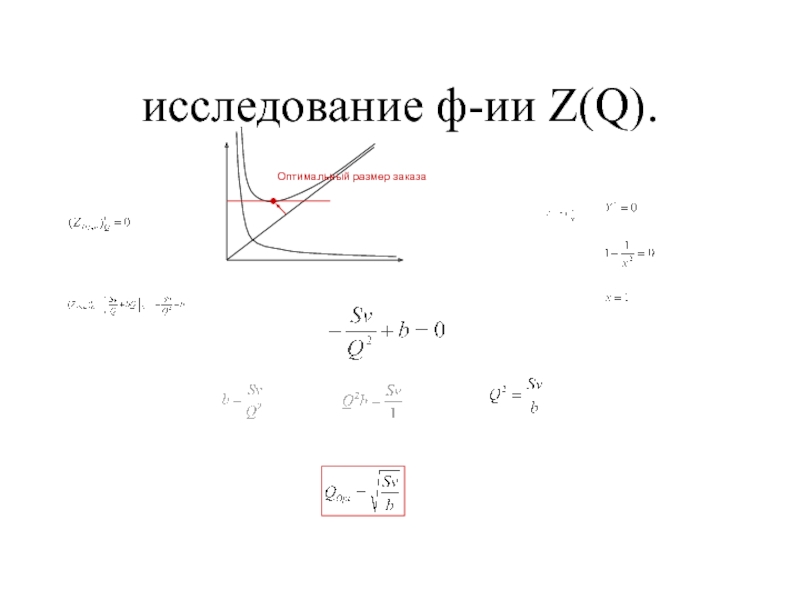
(пункт повышенной сложности). Воспользоваться точным критерием рассчитать из уравнения
(для нашего случая это квадратное уравнение) максимальное (в принятой терминологии - главное) собственное значение и сравнить его с 1, на основании чего сделать вывод о продуктивности матрицы
.
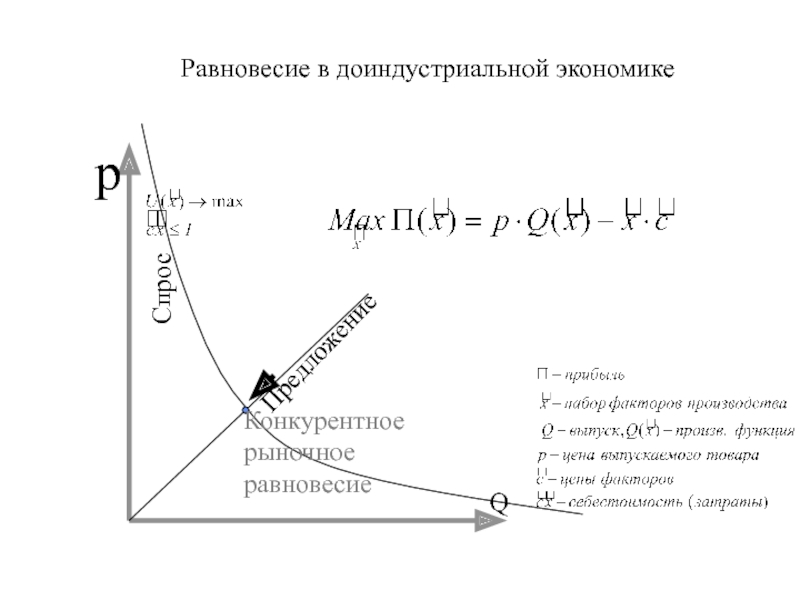
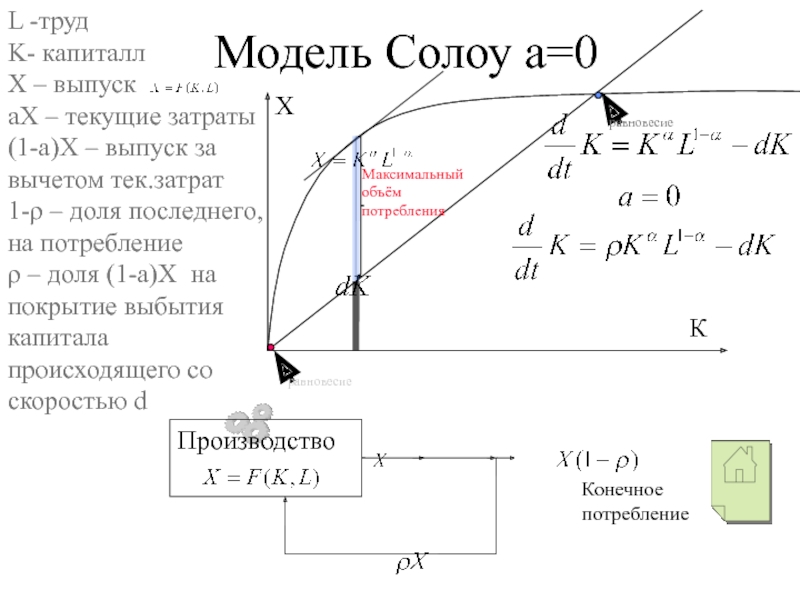
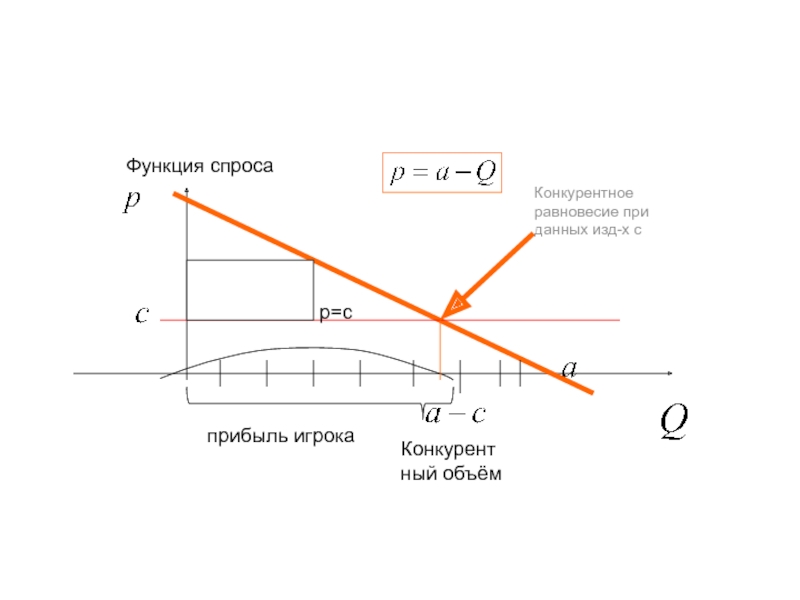
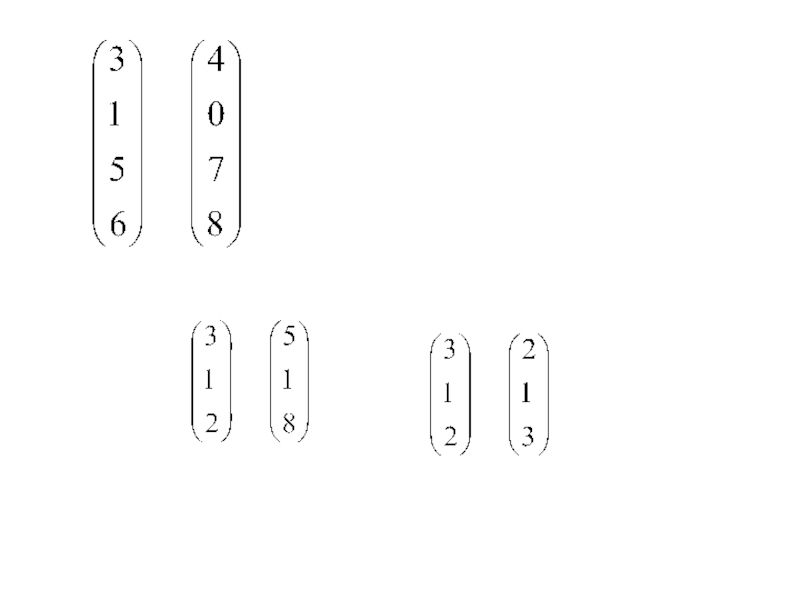
Для вектора конечного потребления
вычислить вектор полного выпуска Х. (т.е. решить уравнение
).
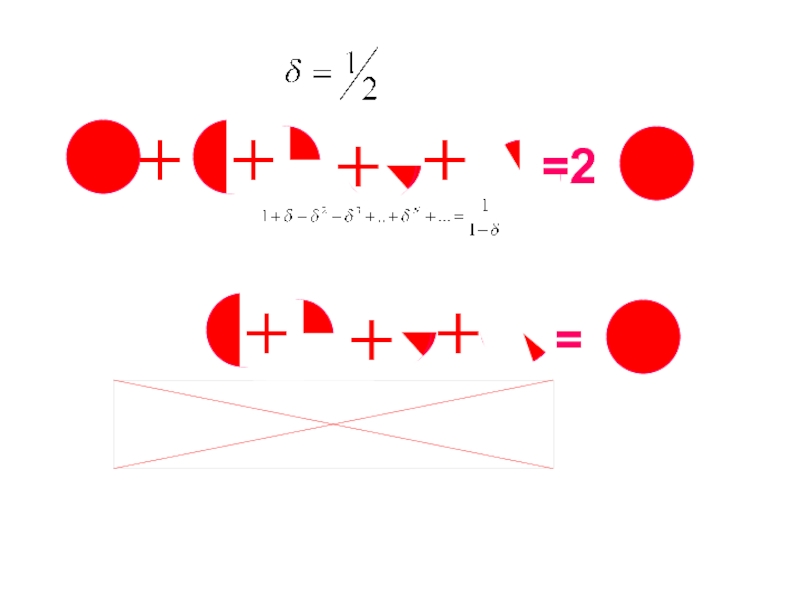
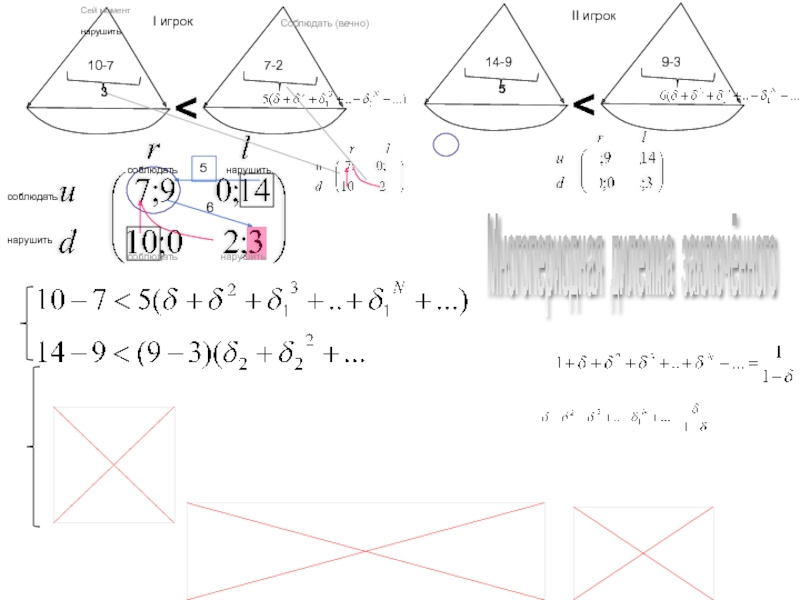
Вычислить несколько первых членов ряда
(каждый член имеет смысл прямых затрат на выпуск предыдущего) и их частичную сумму и сравнить с точным результатом?
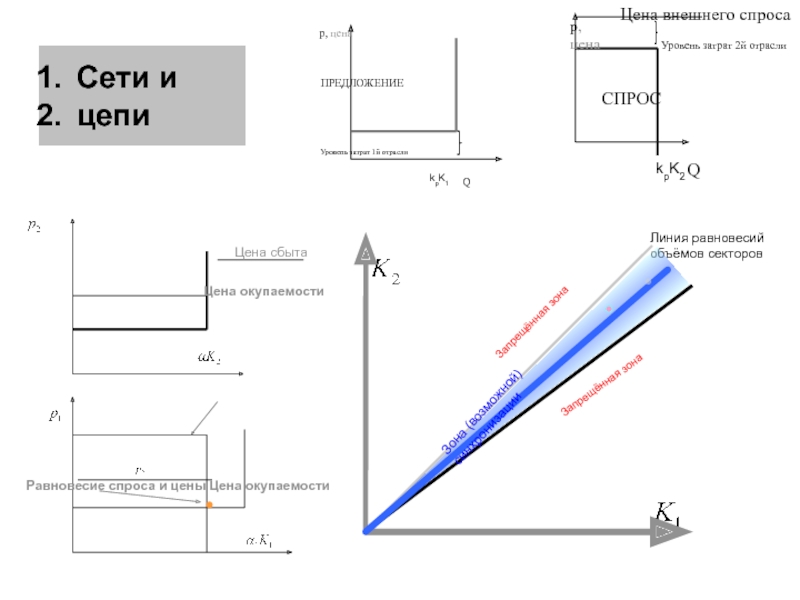
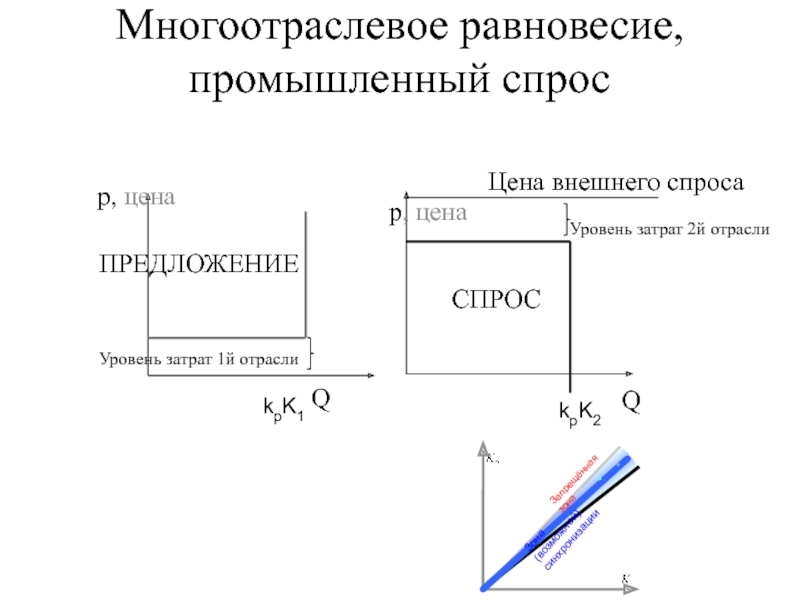
Допустим имеется матрица прямых затрат факторов
и вектор норм прибыли
, выписать нормы прибыли через цены (в дальнейшем это будут правые части линейных уравнений). Разрешить эти уравнения относительно цен
.
склад 2
склад 1
конвейр
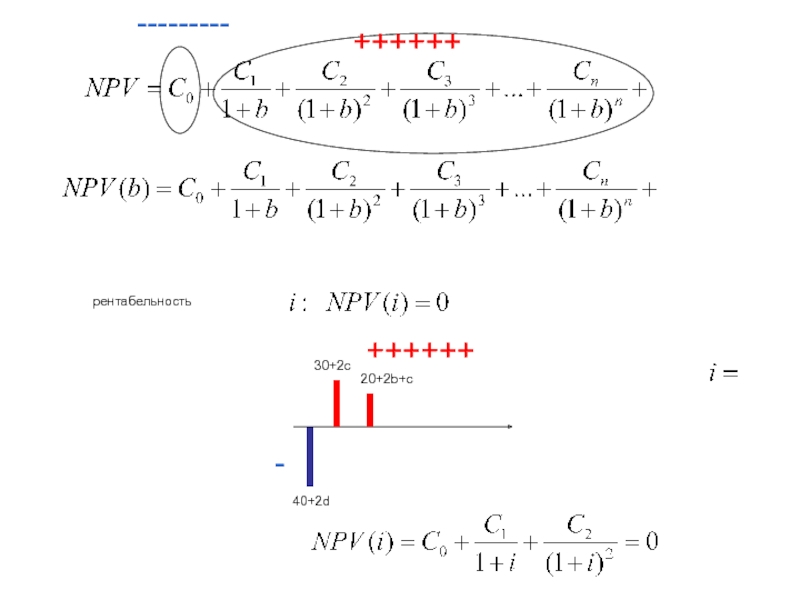
рентабельность