Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Задачи с экономическим содержанием. Вклады. Кредиты. ЕГЭ -2020 Манаенко
Содержание
- 1. Задачи с экономическим содержанием. Вклады. Кредиты. ЕГЭ -2020 Манаенко
- 2. «Нажить много денег - храбрость; сохранить их
- 3. Экономические задачиПод задачами с экономическим содержанием будем понимать задачи,
- 4. Цель занятия: обобщить умения решать
- 5. В ЕГЭ такие задачи входят в задание
- 6. Слайд 6
- 7. Как работает банк
- 8. Что необходимо знать
- 9. КредитыВыбирая кредитную программу, потенциальные заемщики ориентируются на
- 10. Выплаты кредита производятся равными платежами (аннуитет)
- 11. Выплаты кредита подбираются так, что сумма долга уменьшается равномерно (дифференцированный платеж)
- 12. Все представленные в банке ЕГЭ задачи можно
- 13. Задачи на вклады Задача 1.(срок
- 14. 1-й вклад с 1 сентября 2008 года
- 15. Задача 2.(наименьший размер вклада) Вклад планируется
- 16. Решение:
- 17. Задача 3. (наименьший % по вкладу за
- 18. Решение:
- 19. Задача 4. (ежегодное пополнение вклада) В
- 20. Решение: В данной задаче рассматривается вклад с
- 21. Ответ: 210000 руб.
- 22. Задачи на кредиты
- 23. Задача 5. (наибольший %, при котором общая
- 24. Решение: По условию, долг перед банком (в
- 25. Задача 6. (наибольший %, если общая сумма
- 26. Слайд 26
- 27. Задача 7. (нахождение % при разных траншах)
- 28. Слайд 28
- 29. Задача 8. (Нахождение %, если общая сумма
- 30. Слайд 30
- 31. Задача 9. (Кредит на (n+1) месяцев. Нахождение
- 32. Решение:По условию, долг перед банком (в тыс.
- 33. В июле 2020 года планируется взять кредит
- 34. Решение.Долг перед банком (в млн. рублей) на
- 35. Задача 11. (нахождение общей суммы выплат )
- 36. Решение.Ответ: 300000 рублей
- 37. Задача 12. (нахождение суммы долга на определенном
- 38. Решение: Пусть 15-го числа 10-го
- 39. Задача 13. (сумма первоначального вклада) Вклад
- 40. Решение: Пусть первоначальный вклад равен S млн
- 41. Задача 14. (сумма первоначального вклада)В июле планируется
- 42. Решение: Пусть кредит взят на n лет. Обозначим сумму
- 43. Слайд 43
- 44. Спасибо за внимание!!! Адрес для обратной связи: svetlana.manaenko@mail.ru
- 45. Список литературы:1) МАТЕМАТИКА. ЕГЭ. ЗАДАЧА С ЭКОНОМИЧЕСКИМ
- 46. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Задачи с экономическим
содержанием. Вклады. Кредиты.
ЕГЭ -2020
Манаенко Светлана Григорьевна,
учитель математики высшей категории
Слайд 2«Нажить много денег - храбрость;
сохранить их - мудрость,
а
умело расходовать – искусство»
Бертольд Авербах
(нем. писатель)
Слайд 3Экономические задачи
Под задачами с экономическим содержанием будем понимать задачи, поставленные в области
экономики, решение которых требует использования математического аппарата.
Слайд 4 Цель занятия: обобщить умения решать экономические задачи.
Задачи:
повторить разные математические методы при решении экономических задач;
напомнить о различии
между аннуитетным и дифференцированным кредитами;классифицировать некоторые экономические задачи по типам и методам решения.
Слайд 5В ЕГЭ такие задачи входят в задание под № 17.
В
спецификации профильного уровня в графе "примерное время выполнения" задачи повышенной
сложности составляет 35 минут.Элементы содержания, проверяемые
заданием №17: применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учёт реальных
ограничений
Слайд 9Кредиты
Выбирая кредитную программу, потенциальные заемщики ориентируются на процентную ставку по
кредиту. Таких методов существует два: дифференцированные платежи и аннуитетные платежи.
Дифференцированные
платежи характерны тем, что задолженность по кредиту погашается равномерно начиная с самых первых выплат, а проценты начисляются на фактический остаток. Таким образом, каждый последующий платеж меньше предыдущего.Аннуитет — начисление равных платежей на весь срок погашения кредита. При этом в первой половине срока погашения задолженность по кредиту практически не гасится — выплачиваются в большей части проценты. Эта особенность делает платежи относительно небольшими, но увеличивает общую сумму начисляемых процентов.
Слайд 11Выплаты кредита подбираются так, что сумма долга уменьшается равномерно (дифференцированный
платеж)
Слайд 12Все представленные в банке ЕГЭ задачи можно условно разделить
на
группы и подгруппы:
Группа I банковские задачи на вклады
1)
нахождение срока вклада;2) вычисление процентной ставки по вкладу;
3) нахождение суммы вклада;
4) нахождение ежегодной суммы пополнения вклада
Группа II банковские задачи на кредиты:
1) нахождение количества лет выплаты кредита;
2) вычисление процентной ставки по кредиту;
3) нахождение суммы кредита;
4) нахождение ежегодного транша.
Группа III задачи, не связанные с банковскими операциями.
Слайд 13Задачи на вклады
Задача 1.(срок вклада)
Гражданин Петров
по случаю рождения сына открыл 1 сентября 2008 года в
банке счет, на который он ежегодно кладет 1000 рублей. По условиям вклада банк ежегодно начисляет 20% на сумму, находящуюся на счете. Через 6 лет у гражданина Петрова родилась дочь, и 1 сентября 2014 года он открыл в другом банке счет, на который ежегодно кладет по 2200 рублей, а банк начисляет 44% в год. В каком году после очередного пополнения суммы вкладов сравняются, если деньги со счетов не снимают?Слайд 141-й вклад с 1 сентября 2008 года ежегодно - 1000
руб. под 20% . Через 6 лет с 1 сентября 2014
года 2-й вклад ежегодно - 2200 рублей, а банк начисляет 44% в год. В каком году после очередного пополнения суммы вкладов сравняются, если деньги со счетов не снимают? Решение:Слайд 15Задача 2.(наименьший размер вклада)
Вклад планируется открыть на четыре
года. Первоначальный вклад составляет целое число миллионов рублей. В конце
каждого года вклад увеличивается на 10% по сравнению с его размером в начале года, а, кроме этого, в начале третьего и четвёртого годов вклад ежегодно пополняется на 1 млн рублей. Найдите наименьший размер первоначального вклада, при котором через четыре года вклад будет больше 10 млн рублей.Слайд 17Задача 3. (наименьший % по вкладу за определенный срок)
По вкладу «А» банк в течение трёх лет в конце
каждого года увеличивает на 10 % сумму, имеющуюся на вкладе в начале года, а по вкладу « Б» — увеличивает на 11 % в течение каждого из первых двух лет. Найдите наименьшее целое число процентов за третий год по вкладу «Б», при котором за все три года этот вклад всё ещё останется выгоднее вклада «А».Слайд 19Задача 4. (ежегодное пополнение вклада)
В банк помещена сумма
3900 тысяч рублей под 50% годовых. В конце каждого из
первых четырех лет хранения после начисления процентов вкладчик дополнительно вносил на счет одну и ту же фиксированную сумму. К концу пятого года после начисления процентов оказалось, что размер вклада увеличился по сравнению с первоначальным на 725%. Какую сумму вкладчик ежегодно добавлял к вкладу?Слайд 20Решение: В данной задаче рассматривается вклад с пополнением. Обозначим через S
тыс.рублей ежегодную сумму пополнения. 50% годовых означает увеличение вклада в
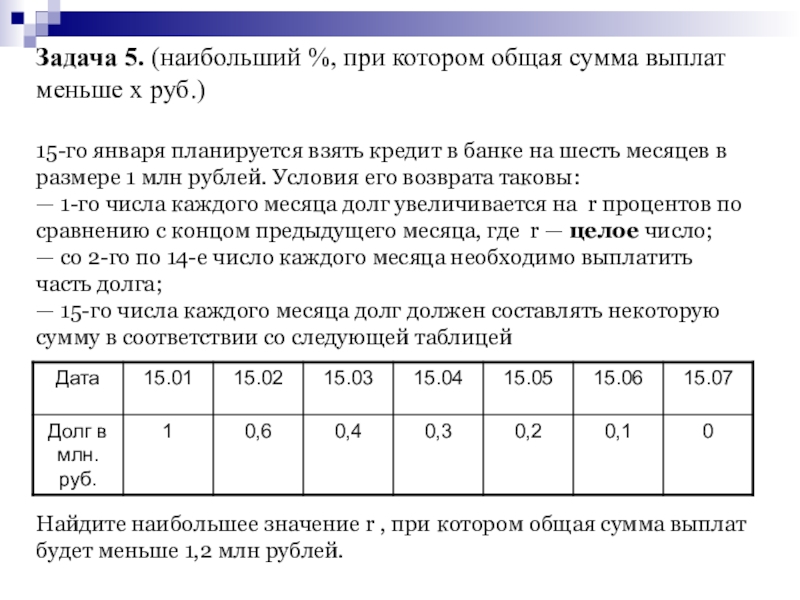
1,5 раза. Тогда сведём данные в таблицу:Слайд 23Задача 5. (наибольший %, при котором общая сумма выплат меньше
х руб.) 15-го января планируется взять кредит в банке на
шесть месяцев в размере 1 млн рублей. Условия его возврата таковы: — 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число; — со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей Найдите наибольшее значение r , при котором общая сумма выплат будет меньше 1,2 млн рублей.Слайд 24Решение: По условию, долг перед банком (в млн рублей) на 15-е число
каждого месяца должен уменьшаться до нуля следующим образом: 1; 0,6;
0,4; 0,3; 0,2; 0,1; 0. Пусть k=1+0,01r, тогда долг на 1-е число каждого месяца равен: k; 0,6k; 0,4k; 0,3k; 0,2k; 0,1k. Следовательно, выплаты со 2-го по 14-е число каждого месяца составляют: k-0,6; 0,6k-0,4; 0,4k-0,3; 0,3k-0,2; 0,2k-0,1; 0,1k . Общая сумма выплат составляет: k(1+0,6+0,4+0,3+0,2+0,1) – (0,6+0,4+0,3+0,2+0,1)=2,6k-1,6 По условию, общая сумма выплат будет меньше 1,2 млн рублей, значит, 2,6k-1,6<1,2; 2,6k<2,8; k<28/26; k<14/13. Значит, 1+0,01r<14/13 0,01r<1/13; r<100/13. Наибольшее целое решение этого неравенства — число 7. Значит, искомое число процентов — 7. Ответ: 7%.
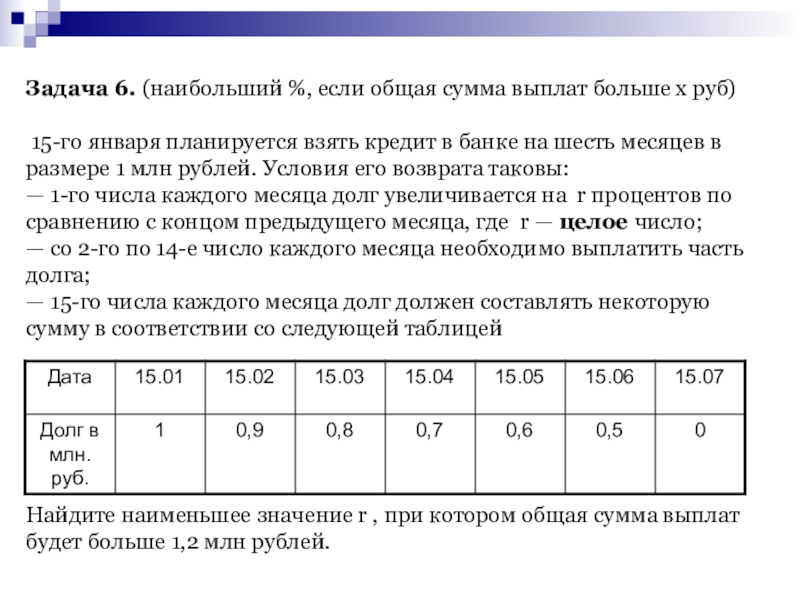
Слайд 25Задача 6. (наибольший %, если общая сумма выплат больше х
руб) 15-го января планируется взять кредит в банке на шесть
месяцев в размере 1 млн рублей. Условия его возврата таковы: — 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число; — со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей Найдите наименьшее значение r , при котором общая сумма выплат будет больше 1,2 млн рублей.Слайд 27Задача 7. (нахождение % при разных траншах)
В июле
2020 года планируется взять кредит в банке на некоторую сумму.
Условия его возврата таковы:— каждый январь долг увеличивается на r % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Если ежегодно выплачивать по 58 564 рубля, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рубля, то кредит будет полностью погашен за 2 года. Найдите r.
Слайд 29Задача 8. (Нахождение %, если общая сумма выплат больше суммы
кредита на n%)
15-го января планируется взять кредит в
банке на 39 месяцев. Условия его возврата таковы:— 1-го числа каждого месяца долг возрастёт на r % по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит. Найдите r.
Слайд 31Задача 9. (Кредит на (n+1) месяцев. Нахождение %)
15-го декабря планируется
взять кредит в банке на сумму 1000000 рублей на (n+1) месяц. Условия
его возврата таковы:— 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по n -й долг должен быть на 40 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— 15-го числа n -го месяца долг составит 200 тысяч рублей;
— к 15-му числу (n+1) -го месяца кредит должен быть полностью погашен.
Найдите r, если известно, что общая сумма выплат после полного погашения кредита составит 1378 тысяч рублей.
Слайд 32Решение:
По условию, долг перед банком (в тыс. рублей) по состоянию
на 15-е число должен уменьшаться до нуля следующим образом:
1000, 960, 920, ..., 240, 200, 0.
Значит,
Первого
числа каждого месяца долг возрастает на r %.Пусть k =1 +0,01r , тогда последовательность размеров долга (в тыс. рублей) по состоянию на 1-е число такова:
1000k, 960k, ..., 240k, 200k.
Следовательно, выплаты (в тыс. рублей) должны быть следующими:
1000(k − 1) + 40, 960(k − 1) + 40, ..., 240(k − 1) + 40, 200k.
Всего следует выплатить (k-1)(1000+960+…+240)+40*20+200k=
Тогда 12 600k − 11 600 = 1378, откуда 12 600k = 12 978, и следовательно, k = 1,03, то есть r = 3.
Ответ: 3.
Слайд 33В июле 2020 года планируется взять кредит в банке на
три года в размере S млн. руб., где S -
целое число. Условия его возврата таковы:- каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
Найдите наибольшее значение S, при котором каждая из выплат будет меньше 4 млн. рублей.
Задача 10. (наибольшее значение кредита, если каждая из выплат меньше некоторой суммы)
Слайд 34Решение.
Долг перед банком (в млн. рублей) на июль каждого года
должен уменьшаться до нуля следующим образом:
S; 0,8S; 0,5S; 0
По условию,
в январе каждого года долг увеличивается на 25%, значит, долг в январе каждого года равен:1,25S; 1,25∙0,8S; 1,25∙0,5S
Следовательно, выплаты с февраля по июнь каждого года составляют:
1,25S - 0,8S = 0,45S
1,25∙0,8S - 0,5S = 0,5S
1,25∙0,5S – 0 = 0,725S
По условию, каждая из выплат должна быть меньше 4 млн. рублей.
Это будет верно, если максимальная из выплат меньше 4 млн.рублей, т. е.
0,725S< 4;
S< 6,4
S = 6
Наибольшее целое решение этого неравенства – число 6. Значит, искомый размер кредита 6 млн. рублей. Ответ: 6 млн. руб.
Слайд 35Задача 11. (нахождение общей суммы выплат )
Взяли кредит
177 120 рублей в банке на четыре года под 25% годовых
и выплатили четырьмя равными платежами. Чему будет равна общая сумма выплат после полного погашения кредита?Слайд 37Задача 12. (нахождение суммы долга на определенном сроке)
15-го декабря планируется
взять кредит в банке на 11 месяцев. Условия его возврата
таковы:— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 10-й долг должен быть на 80 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 11-го месяца кредит должен быть полностью погашен.
Какой долг будет 15-го числа 10-го месяца, если общая сумма выплат после полного погашения кредита составит 1198 тысяч рублей?
Слайд 38Решение:
Пусть 15-го числа 10-го месяца долг
составит Х тысяч рублей.
По условию, долг перед банком
(в тыс. рублей) по состоянию на 15-е число должен уменьшится до нуля следующим образом: х+800;х+720;…;х+80;х;0.
Первого числа каждого месяца долг возрастает на 3%, увеличивается в 1,03 раза, значит, последовательность размеров долга (в тыс. рублей) по состоянию на 1-е число такова:
1,03(х+800); 1,03(х+720); …;1,03(х+80); 1,03х.
Следовательно, выплаты (в тыс. рублей) должны быть следующими:
1,03(х+800)-(х+800)+80; 1,03(х+720)-(х+720)+80; …;1,03(х+80)-(х+80)+80; 1,03х.
Упростим и получим
0,03(х+800)+80; 0,03(х+720)+80; …;0,03(х+80)+80; 1,03х.
Всего следует выплатить (тыс. рублей):
0,03(х+800)+80 + 0,03(х+720)+80 + …+0,03(х+80)+80+ 1,03х= 0,03(10х+800+720+…+80)+80*10+1,03х= 0,03*(10х+4400)+800+1,03х=932+1,33х
откуда 932+1,33х=1198
х=200
Значит, 15-го числа 10-го месяца долг составит 200 тыс. рублей.
Ответ: 200 тысяч рублей.
Слайд 39Задача 13. (сумма первоначального вклада)
Вклад планируется открыть на
четыре года. Первоначальный вклад составляет целое число миллионов рублей. В конце каждого
года вклад увеличивается на 10% по сравнению с его размером в начале года, а, кроме этого, в начале третьего и четвёртого годов вклад ежегодно пополняется на 1 млн рублей. Найдите наименьший размер первоначального вклада, при котором через четыре года вклад будет больше 10 млн рублей.Слайд 40Решение:
Пусть первоначальный вклад равен S млн рублей.
Тогда в конце 1-го года вклад составит 1,1S, а в
конце 2-го — 1,21S.В начале 3-го года вклад составит 1,21S + 1, а в конце — (1,21S+1)1,1=1,331S + 1,1.
В начале 4-го года вклад составит 1,331S + 2,1,
а в конце — (1,331S + 2,1)1,1=1,4641S + 2,31.
По условию, нужно найти наибольшее целое S, для которого выполнено неравенство
1,4641S + 2,31>10,
откуда 1,4641S>7,69;
S>5,25.
Наименьшее целое решение этого неравенства — число 5. Значит, размер первоначального вклада составляет 5 млн рублей.
Ответ: 5 млн рублей.
Слайд 41Задача 14. (сумма первоначального вклада)
В июле планируется взять кредит в
банке на сумму 16 млн. рублей на некоторый срок (целое число лет).
Условия его возврата таковы:—каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 38 млн рублей?
Слайд 42Решение:
Пусть кредит взят на n лет. Обозначим сумму кредита S = 16 млн руб,
а процентную ставку — r=0,25
В соответствии с условием задачи заполним
таблицу:Слайд 45Список литературы:
1) МАТЕМАТИКА. ЕГЭ. ЗАДАЧА С ЭКОНОМИЧЕСКИМ СОДЕРЖАНИЕМ: УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ.
/ ПОД РЕД. Ф.Ф.ЛЫСЕНКО И С.Ю.КУЛАБУХОВА, РОСТОВ-НА-ДОНУ:ЛЕГИОН, 2019. – 80С. 2)
ЕГЭ. МАТЕМАТИКА. ПРОФИЛЬНЫЙ УРОВЕНЬ: ТИПОВЫЕ ЭКЗАМЕНАЦИОННЫЕ ВАРИАНТЫ: 36 ВАРИАНТОВ / ПОД РЕД. И.В.ЯЩЕНКО, ИЗДАТЕЛЬСТВО “НАЦИОНАЛЬНОЕ ОБРАЗОВАНИЕ”, 2019 – 256С.3) Д.Д.ГУЩИН, КУРС ЛЕКЦИЙ ПО ПОДГОТОВКЕ К ЕГЭ.
ВЕБ-СТРАНИЦА КУРСА С АКТУАЛЬНЫМИ МАТЕРИАЛАМИ: HTTP://RESHUEGE.RU/COURSE?ID=2610 ИЗДАНИЕ 2, ДОПОЛНЕННОЕ. — 05.04.2016