Слайд 1Квантовая механика и развитие информационных технологий
(вводная лекция)
Физико-технологический институт
РАН
По материалам доклада на
Московском Суперкомпьютерном Форуме.
Москва, ВВЦ, 26 октября
2011
Ю.И. Богданов
Квантовая
Информатика
Слайд 2Закон Мура и развитие информационных технологий
Мотивация квантовых вычислений - алгоритмическая
сложность.
Кубиты вместо битов.
Многокубитовые системы - запутанность как основной ресурс квантовых
вычислений.
Идеальная схема квантового компьютера.
Реализация квантовых компьютеров - ионы в ловушках, ЯМР, квантовые точки, сверхпроводники.
Контроль квантовых состояний - квантовая томография.
Заключение.
План доклада:
Слайд 3 Закон Мура и развитие информационных технологий
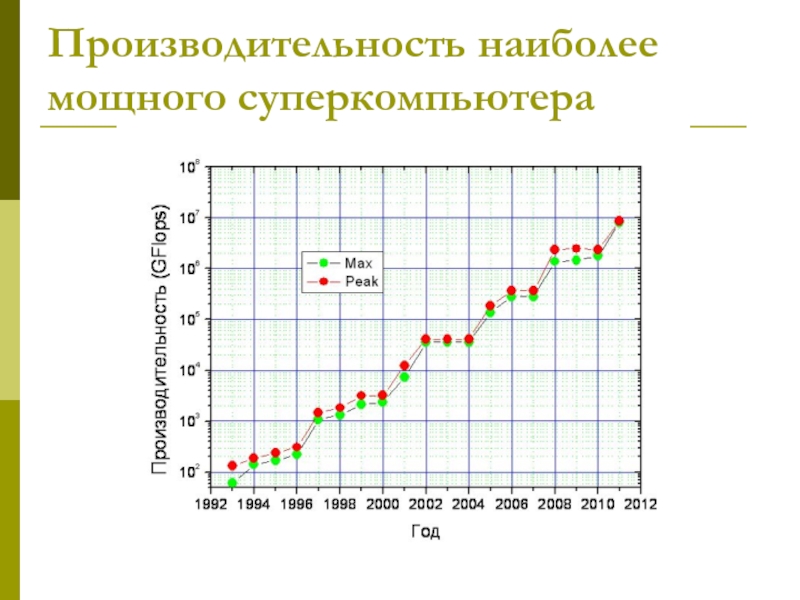
Слайд 4Производительность наиболее мощного суперкомпьютера
Слайд 5Основные проблемы, мешающие увеличению производительности суперкомпьютеров.
Энергопотребление. Сейчас наиболее мощный суперкомпьютер
из TOP 500, установленный в Японии потребляет 9,9 мегаватта электроэнергии,
что соответствует выходной мощности небольшой электростанции и достаточно, чтобы поддерживать жизнедеятельность города с населением в 40 тыс. человек. Год назад наиболее мощный компьютер потреблял 4.4 мегаватта, а в 2009 2.48 мегаватта. При использовании существующих технологий для достижения экзафлопсной производительности счет пойдет уже на ГВатты энергии.
Эффективность межпроцессорного обмена. При увеличении количества процессоров общая производительность начинает упираться в скорость обмена данными между процессорами.
Надежность. При росте числа вычислительных узлов надежность системы также снижается по экспоненте.
Слайд 6Разложение числа на простые множители
Умножение многозначных чисел- простая задача, обратная
задача (разложение на множители)- очень сложная
Метод решета числового поля (наилучший
известный классический алгоритм)
Алгоритм Шора (1994)
число десятичных знаков
число двоичных знаков
Слайд 7Если бы Вселенная была компьютером
Вселенная как суперкомпьютер
Число нуклонов во
Вселенной
Гц, «тактовая» частота, определяемая временем пролёта света через протон
Полное число
операций за время существования Вселенной – ресурс, достаточный для разложения числа с 12 тысячами знаков по классическому алгоритму, квантовый мегагерцовый компьютер решает задачу за 5 часов
Seth Lloyd Computational Capacity of the Universe// Phys. Rev. Lett. 2002,V.88, 237901
Оценка информационного ресурса Вселенной, полученная проф. Ллойдом из MIT из других соображений
Слайд 8Feynman R. Simulating Physics with Computers // Int. J. Theor.
Phys. 1982. V.21. №6/7. P.467-488.
Feynman R. Quantum Mechanical Computers
// Found. of Phys. 1986. V.16. №6. P.507-531.
Манин Ю.И. Вычислимое и невычислимое. М. Советское Радио. 1980. 128с.
Ричард Фейнман
Юрий Манин
Идея квантовых вычислений
Слайд 9Разложение числа на простые множители
Динамика сложных квантовых систем (конденсированные среды,
белки, ДНК и др.)
Алгоритмы полиномиальной сложности: число операций (время решения задачи) растет полиноминально с ростом объема входных данных (класс P)
Алгоритмы неполиномиальной (например, экспоненциальной) сложности: требуют практически экспоненциально большого числа операций и/или экспоненциально большого объема памяти
Алгоритмическая сложность
Слайд 10Алгоритм поиска по неструктурированной базе данных (решение произвольного булевского уравнения
f(x1,x2,…,xn)=1 )
В классическом случае требует, очевидно, O(2n) вычислений f(x). Такая
сложность никак не может быть улучшена на классическом компьютере.
Алгоритм Гровера (1996)
Квантовый алгоритм Гровера решает задачу за O(2n/2), давая неоспоримое квадратичное преимущество.
Позволяет решать некоторые NP-полные задачи с квадратичным ускорением, относительно известных методов.
Слайд 11Кубит vs. бит
-импульс
- импульс
В основе кубита лежит естественное
квантование информации,
в основе бита- искуственная дискретизация аналогового сигнала.
Статистическая
неопределённость квантовых систем является управляемой. Чистые квантовые состояния не несут в себе никакой энтропийной неопределённости.
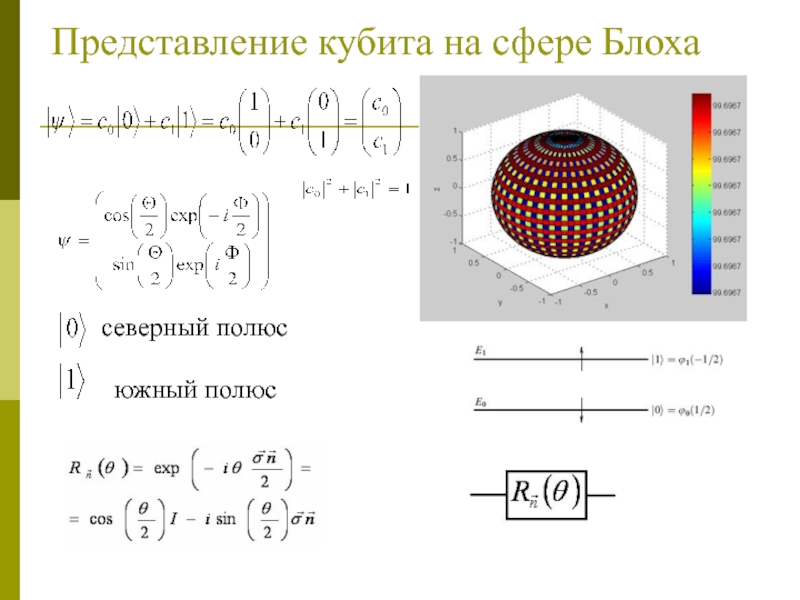
Слайд 12Представление кубита на сфере Блоха
северный полюс
южный полюс
Слайд 13Двухкубитовые состояния
если
(запутанность состояний)
-запутанное состояние (синглет)
- незапутанное состояние
Слайд 14трёхкубитовое состояние- 8 комплексных параметров
Многокубитовые состояния
n-кубитовые состояния
комплексных параметров
действительных физически значимых
параметров для состояния общего вида
-действительных параметров для незапутанного состояния
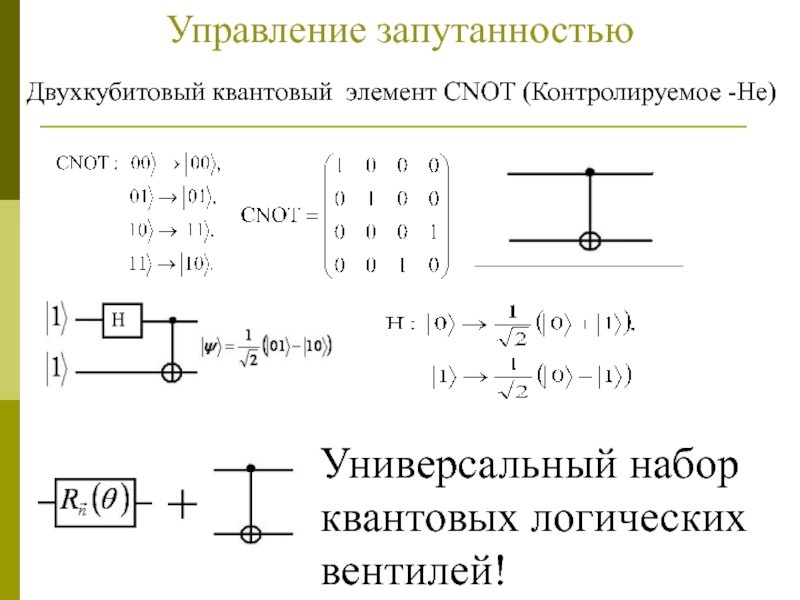
Слайд 15Управление запутанностью
Универсальный набор квантовых логических вентилей!
Двухкубитовый квантовый элемент CNOT
(Контролируемое -Не)
Слайд 16Схема идеального квантового
компьютера
Валиев К.А. Квантовые компьютеры и квантовые вычисления
// УФН, 2005. Т.175, №1. стр.3-39.
DiVincenzo D.P. The Physical Implementation of
Quantum Computation. // Fortschr. der Phys., 2000, V.48, № 9-11, pp.771-783, arXiv:quant-ph/0002077.
Слайд 17Квантовый параллелизм
Состояние квантового компьютера имеет 2n комплексных амплитуд, что несет
в себе огромные информационные мощности.
a00…00
a00…01
a00…11
a11…10
a11…11
…
Любая (даже однокубитная) операция
b00…00
b00…01
b00…11
b11…10
b11…11
…
Меняются все амплитуды
состояния квантового компьютера.
Слайд 18Квантовый компьютер на ионах в ловушках:
модель Цирака и Цоллера,
Институт теоретической физики (Австрия), 1995
Cirac J.I., Zoller P. Quantum Computation with Cold
Trapped Ions // Phys.Rev.Lett., 1995, V.74, p.4094.
Слайд 19Monroe C., Meerkhof D.M., King B.E., Itano W.M., Wineland D.J
Demonstration of a Fundamrntal Quantum Logic Gate // Phys. Rev. Lett.
1995, V.75, p. 4714
Первый эксперимент на ионах в ловушках:
группа NIST (США), 1995
Слайд 20
Экспериментальная реализация элемента Тоффоли на ионах кальция в ловушке Пауля
–
Институт экспериментальной физики (Австрия)- 2009
T. Monz et al. Realization of
the Quantum Toffoli Gate with Trapped Ions // Phys. Rev. Lett. 2009, V.102, 04501
Слайд 21Ионы в многозонных ловушках:
группа NIST (США), 2009
R. B.
Blakestad et al. High-Fidelity Transport of Trapped-Ion Qubits through an
X-Junction Trap Array // Phys. Rev. Lett. 2009, v.102, 153002
46 управляющих электродов, 18 зон захвата
транспорт ионов бериллия
с вероятностью 0.9999 и
разогревом менее
Слайд 2214-кубитовые запутанные состояния
Институт экспериментальной физики (Австрия)- 2011
T. Monz et
al. 14-Qubit Entanglement: Creation and Coherence // Phys. Rev. Lett.
2011. V.106, 130506
Генерация GHZ- состояний на ионах в ловушках
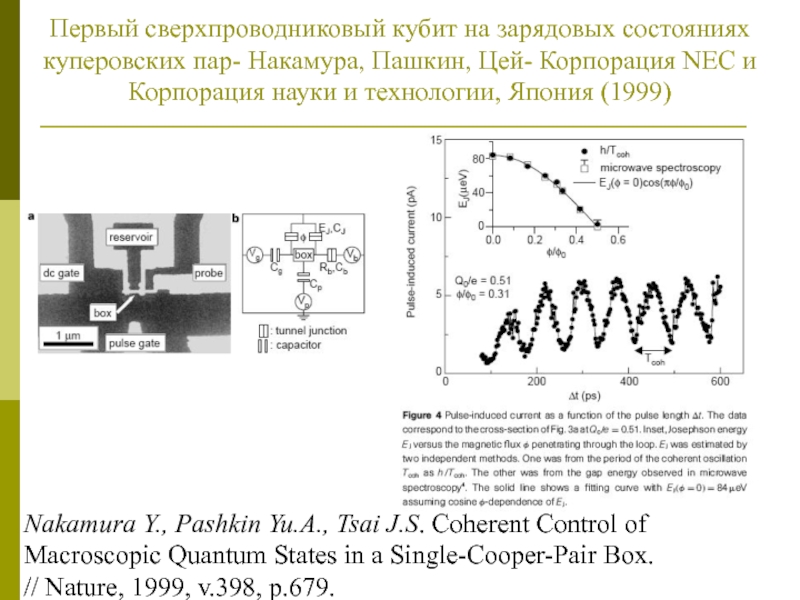
Слайд 23Первый сверхпроводниковый кубит на зарядовых состояниях куперовских пар- Накамура, Пашкин,
Цей- Корпорация NEC и Корпорация науки и технологии, Япония (1999)
Nakamura
Y., Pashkin Yu.A., Tsai J.S. Coherent Control of
Macroscopic Quantum States in a Single-Cooper-Pair Box.
// Nature, 1999, v.398, p.679.
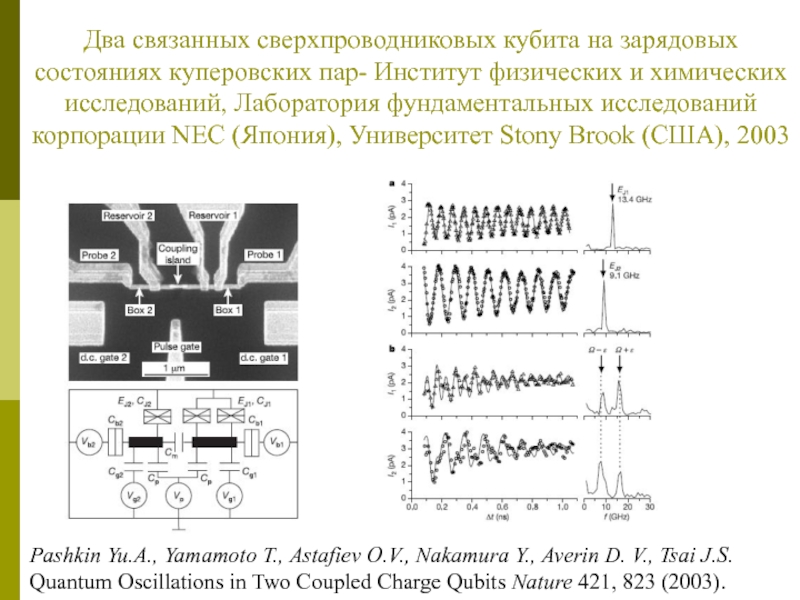
Слайд 24Два связанных сверхпроводниковых кубита на зарядовых состояниях куперовских пар- Институт
физических и химических исследований, Лаборатория фундаментальных исследований корпорации NEC (Япония),
Университет Stony Brook (США), 2003
Pashkin Yu.A., Yamamoto T., Astafiev O.V., Nakamura Y., Averin D. V., Tsai J.S. Quantum Oscillations in Two Coupled Charge Qubits Nature 421, 823 (2003).
Слайд 25Демонстрация двухкубитовых операций на сверхпроводниковых зарядовых кубитах
Yamamoto T., Pashkin Yu.
A., Astafiev O.V., Nakamura Y., and Tsai J.S. Demonstration of
Conditional Operation Using Superconducting Charge Qubits // Nature 2003, V.425, p.941.
Слайд 26Кубит на квантовых состояниях магнитного потока: интерференция флюксоидных состояний ,
2000- Университет Stony Brook (США)
Friedman J.R.,Patel V., Chen W., Tolpygo
S.K., Lurens J.,E. Quantum Superposition
of Distinct Macroscopic States. // Nature, 2000, V.406, p.43
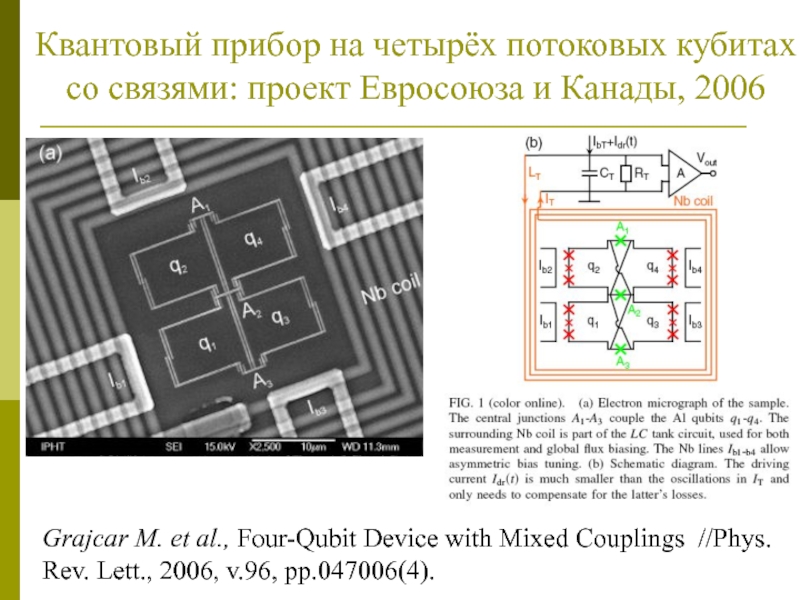
Слайд 27Квантовый прибор на четырёх потоковых кубитах со связями: проект Евросоюза
и Канады, 2006
Grajcar M. et al., Four-Qubit Device with Mixed
Couplings //Phys. Rev. Lett., 2006, v.96, pp.047006(4).
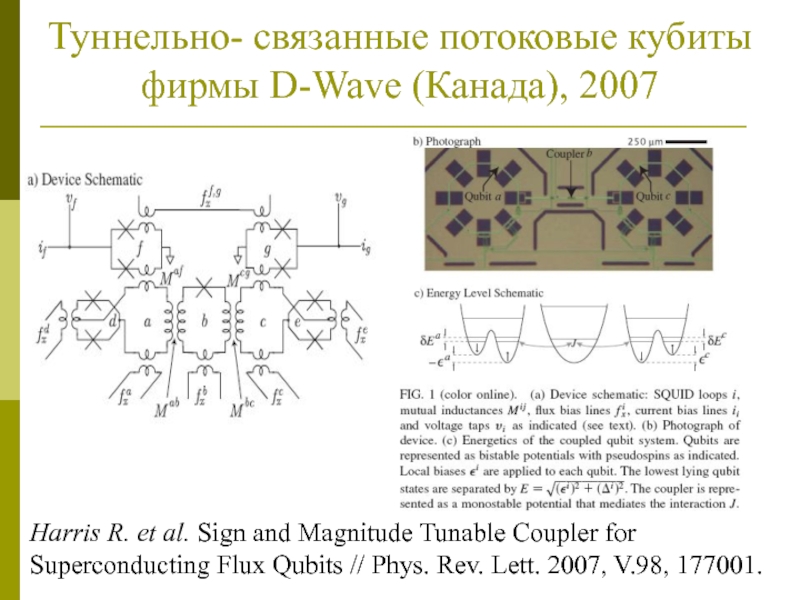
Слайд 28Туннельно- связанные потоковые кубиты фирмы D-Wave (Канада), 2007
Harris R. et
al. Sign and Magnitude Tunable Coupler for Superconducting Flux Qubits
// Phys. Rev. Lett. 2007, V.98, 177001.
Слайд 29Реализация алгоритма Гровера на двухкубитовом сверхпроводниковом процессоре -Йельский университет (США)
совместно с коллегами из Канады и Австрии,2009
L. DiCarlo et al.
Demonstration of two-qubit algorithms with a superconducting quantum processor // Nature. 2009. V.460. P.240-244
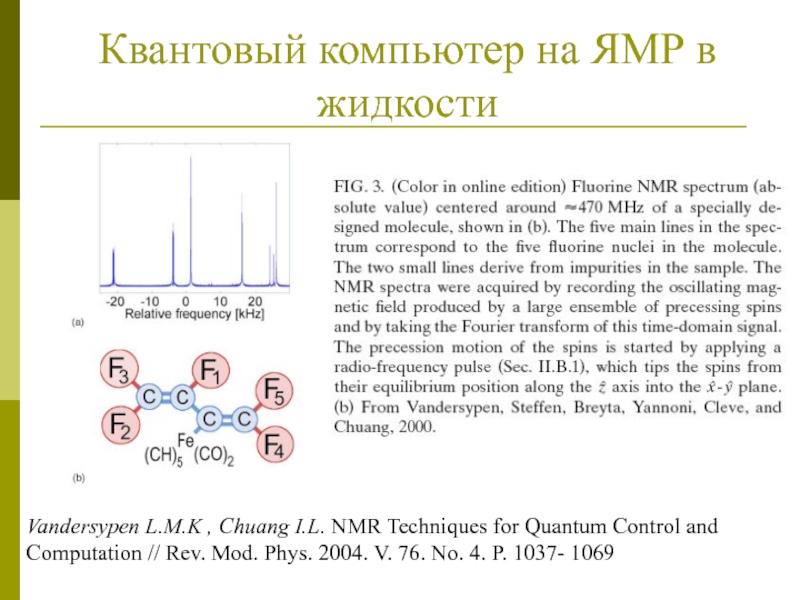
Слайд 30Квантовый компьютер на ЯМР в жидкости
Vandersypen L.M.K , Chuang I.L.
NMR Techniques for Quantum Control and Computation // Rev. Mod.
Phys. 2004. V. 76. No. 4. P. 1037- 1069
Слайд 31Модель Кейна кремниевого квантового компьютера на ядерных спинах донорных атомов
фосфора с индивидуальным обращением к кубитам-Университет Нового Южного Уэльса, Австралия
Kane
B.E. A Silicon-Based nuclear Spin Quantum Computer// Nature, 1998, v.393, N.5, pp.133–137.
Слайд 32Ансамблевый квантовый компьютер на ядерных спинах- модель ФТИАН
Валиев К.А., Кокин
А.А. Полупроводниковые ЯМР квантовые компьютеры с индивидуальным и ансамблевым обращением
к кубитам // Микроэлектроника. 1999. Т.28. №5. С.326-337.
Кокин А.А. Твердотельные квантовые компьютеры на ядерных спинах. – Москва-Ижевск: ИКИ, 2004, 204 с.
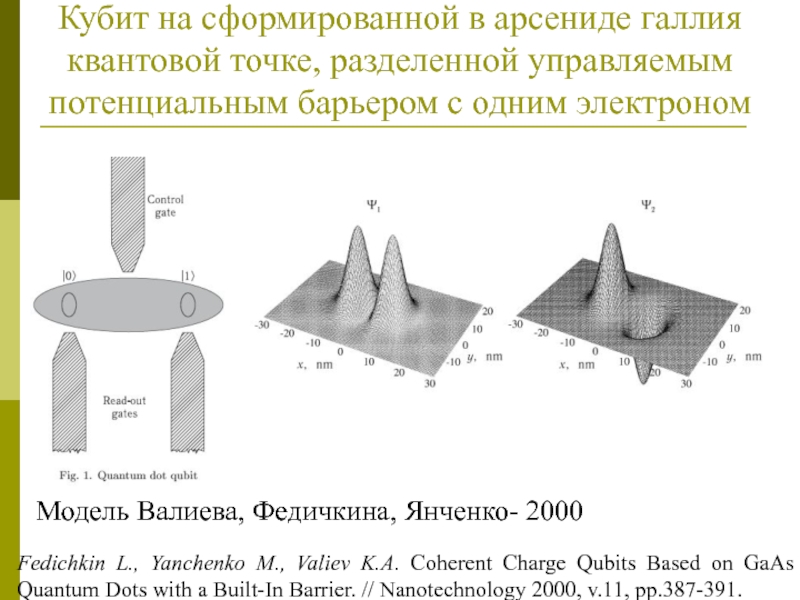
Слайд 33Модель Валиева, Федичкина, Янченко- 2000
Fedichkin L., Yanchenko M., Valiev K.A.
Coherent Charge Qubits Based on GaAs Quantum Dots with a
Built-In Barrier. // Nanotechnology 2000, v.11, pp.387-391.
Кубит на сформированной в арсениде галлия квантовой точке, разделенной управляемым потенциальным барьером с одним электроном
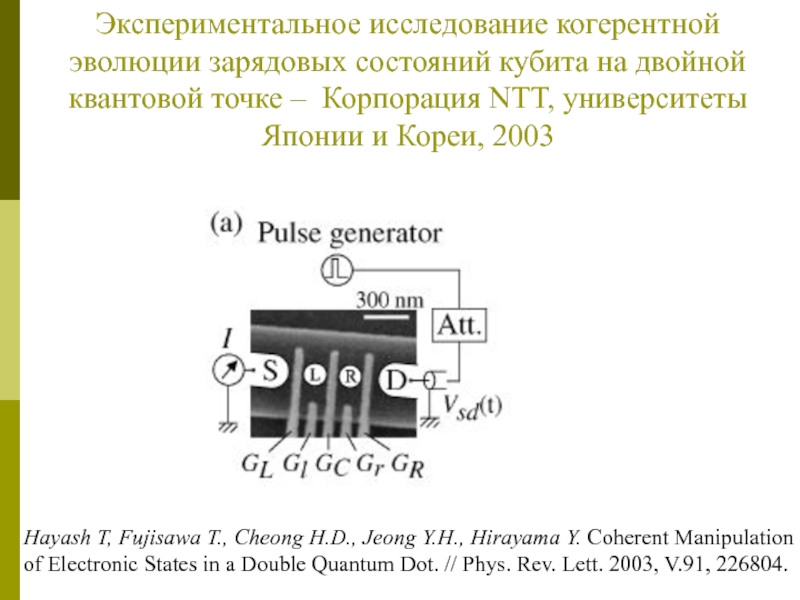
Слайд 34Hayash T, Fujisawa T., Cheong H.D., Jeong Y.H., Hirayama Y.
Coherent Manipulation of Electronic States in a Double Quantum Dot.
// Phys. Rev. Lett. 2003, V.91, 226804.
Экспериментальное исследование когерентной эволюции зарядовых состояний кубита на двойной квантовой точке – Корпорация NTT, университеты Японии и Кореи, 2003
Слайд 35Экспериментальное исследование связанных полупроводниковых зарядовых кубитов -Корпорация NTT совместно с
Токийским университетом (Япония), 2009
Gou Shinkai et al. Correlated Coherent Oscillations
in Coupled Semiconductor Charge Qubits // Phys. Rev. Lett. 2009, v.103, 056802
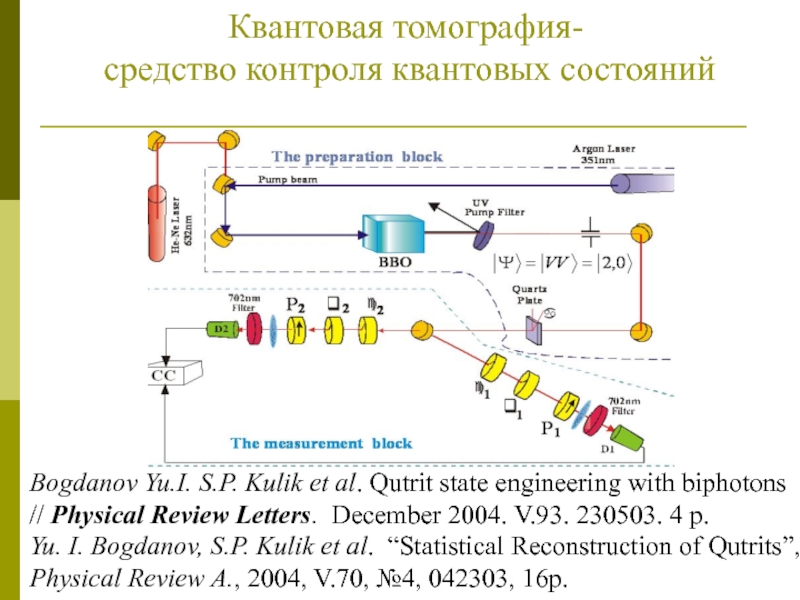
Слайд 36Bogdanov Yu.I. S.P. Kulik et al. Qutrit state engineering with
biphotons // Physical Review Letters. December 2004. V.93. 230503. 4
p.
Yu. I. Bogdanov, S.P. Kulik et al. “Statistical Reconstruction of Qutrits”, Physical Review A., 2004, V.70, №4, 042303, 16p.
Квантовая томография-
средство контроля квантовых состояний
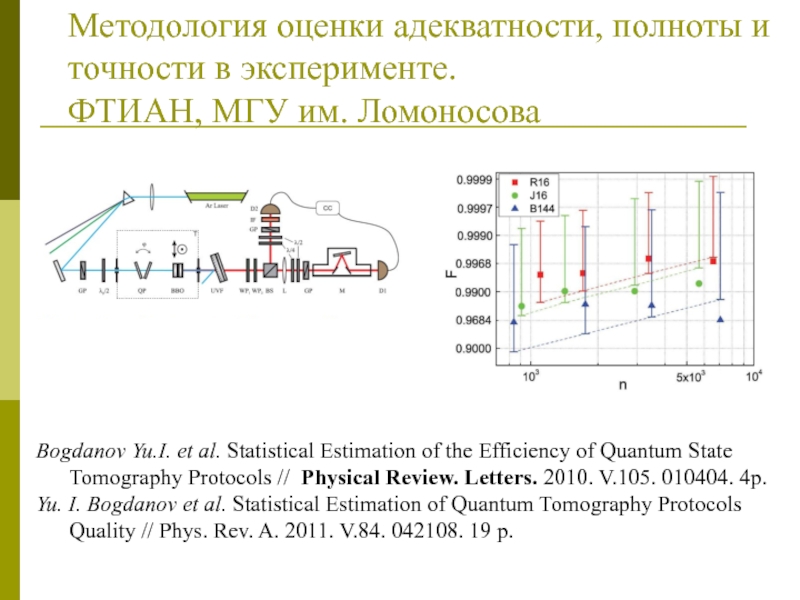
Слайд 37Методология оценки адекватности, полноты и точности в эксперименте.
ФТИАН, МГУ им.
Ломоносова
Bogdanov Yu.I. et al. Statistical Estimation of the Efficiency
of Quantum State Tomography Protocols // Physical Review. Letters. 2010. V.105. 010404. 4p.
Yu. I. Bogdanov et al. Statistical Estimation of Quantum Tomography Protocols Quality // Phys. Rev. A. 2011. V.84. 042108. 19 p.
Слайд 38Универсальный метод томографии квантовых состояний, основанный на процедуре очищения (модель
ФТИАН)
Преимущества:
Восстановление квантовых состояний в гильбертовом пространстве высокой размерности
Разработка универсальной теории
статистических флуктуаций квантовых состояний
Обеспечение точности, близкой к фундаментальному пределу
Применение метода к экспериментам в области квантовой оптики позволило обеспечить точность, существенно превышающую точность, полученную в других работах
Слайд 39Квантовые компьютеры, когда они будут созданы, позволят решать задачи, недоступные
классическим компьютерам.
-В основе квантового компьютера лежит квантовый бит, двухуровневая
квантовая система.
-Основным ресурсом квантовых вычислений служит явление запутанности, не имеющее классического аналога.
Заключение
Слайд 40Любое квантовое вычисление может быть выполнено с помощью универсального набора
одно- и двухкубитовых элементарных операций.
Предложены различные варианты квантовых компьютеров:
на ионах в ловушках, на ядерных спинах, на квантовых точках, на сверхпроводниках.
- Основное препятствие на пути создания квантовых компьютеров - декогерентизация, неконтролируемое взаимодействием квантовой системы с окружением.
Заключение (прод.)