Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Законы распределения случайных величин
Содержание
- 1. Законы распределения случайных величин
- 2. ЧТО НУЖНО ВСПОМНИТЬ:переменная, которая в зависимости от
- 3. ЗАКОН РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫСлучайная величина считается заданной,
- 4. РЯД РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫРяд распределения – это
- 5. ПОЛИГОН РАСПРЕДЕЛЕНИЯ - ПРИМЕРСлучайная величина X – количество очков, выпадающих при бросании двух кубиков
- 6. Пример дваПо прогнозу погоды от 21.03.2019температура воздуха
- 7. Пример дваТемпература воздуха – непрерывная случайная величина.Закон
- 8. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯЕе еще называют интегральной функцией распределения.
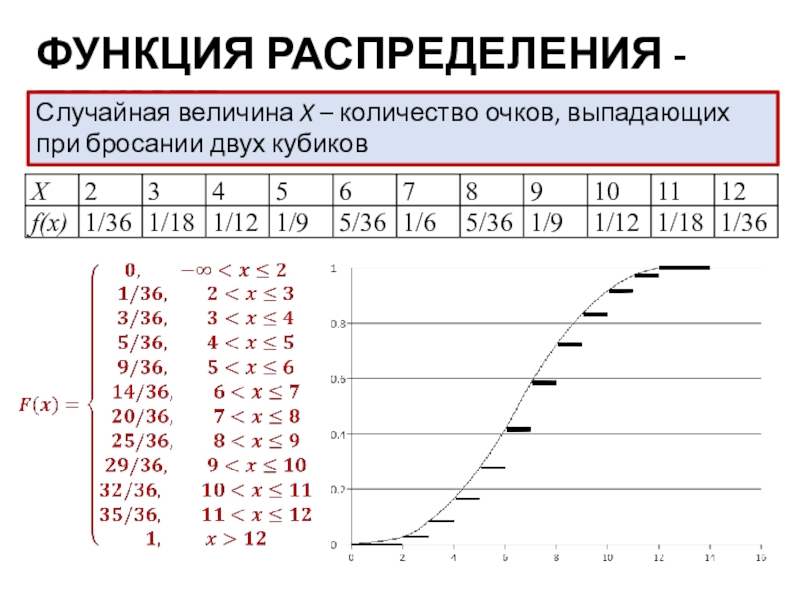
- 9. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ - ПРИМЕРСлучайная величина X – количество очков, выпадающих при бросании двух кубиков
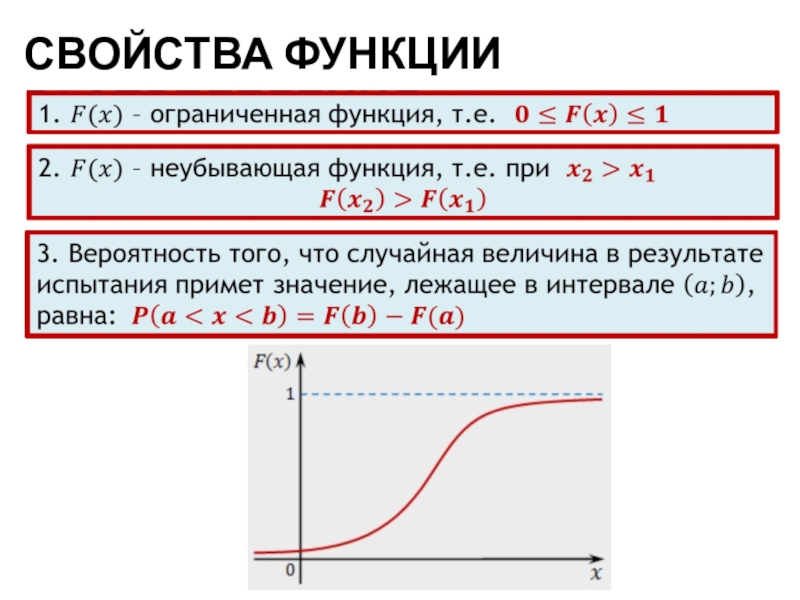
- 10. СВОЙСТВА ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
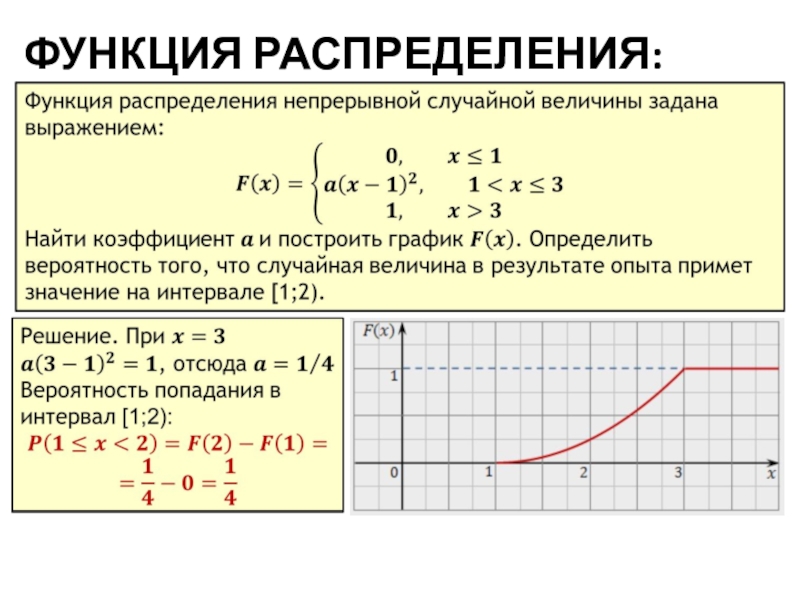
- 11. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ: ПРИМЕР
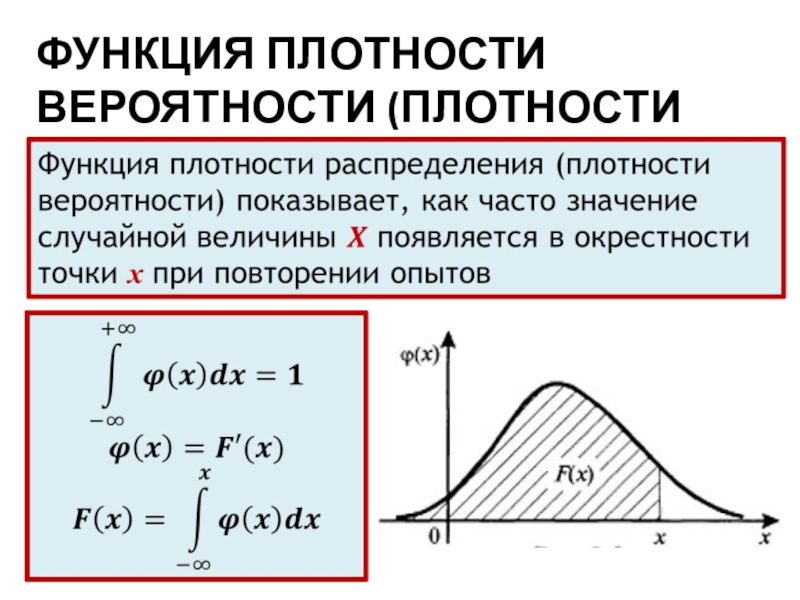
- 12. ФУНКЦИЯ ПЛОТНОСТИ ВЕРОЯТНОСТИ (ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ)
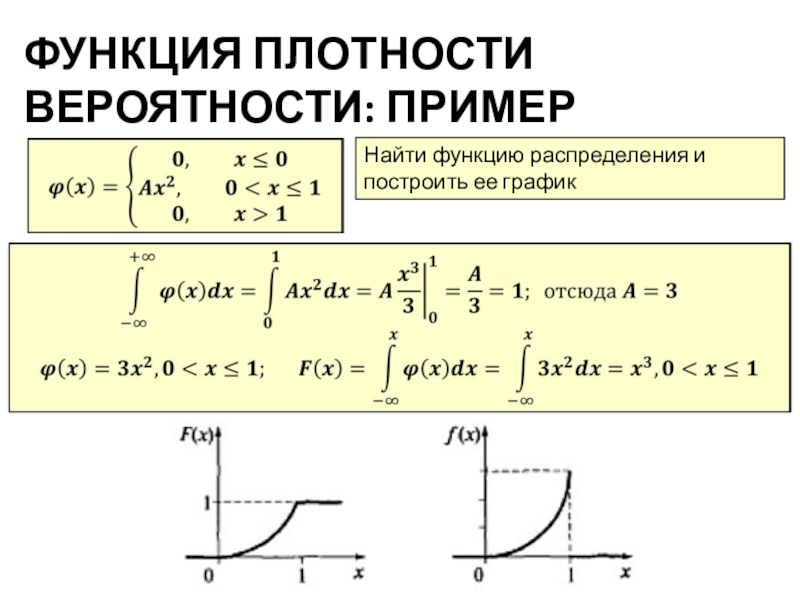
- 13. ФУНКЦИЯ ПЛОТНОСТИ ВЕРОЯТНОСТИ: ПРИМЕРНайти функцию распределения и построить ее график
- 14. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИНматематическое ожидание, дисперсия, моменты различных порядков, мода и медиана.
- 15. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕM(X)=0∙0.2231 + 1∙0.3347 + 2∙0.2510 +
- 16. СВОЙСТВА МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ1. Математическое ожидание суммы двух
- 17. ДИСПЕРСИЯДисперсией называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:D(X) = M((X – M(X))2)
- 18. Найти математическое ожидание и дисперсию случайной величины
- 19. Законы распределения непрерывных случайных величин1. Равномерное распределение2. Показательное (экспоненциальное) распределение3. Нормальное распределение
- 20. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
- 21. Равномерное распределение.Непрерывная случайная величина имеет равномерное распределение
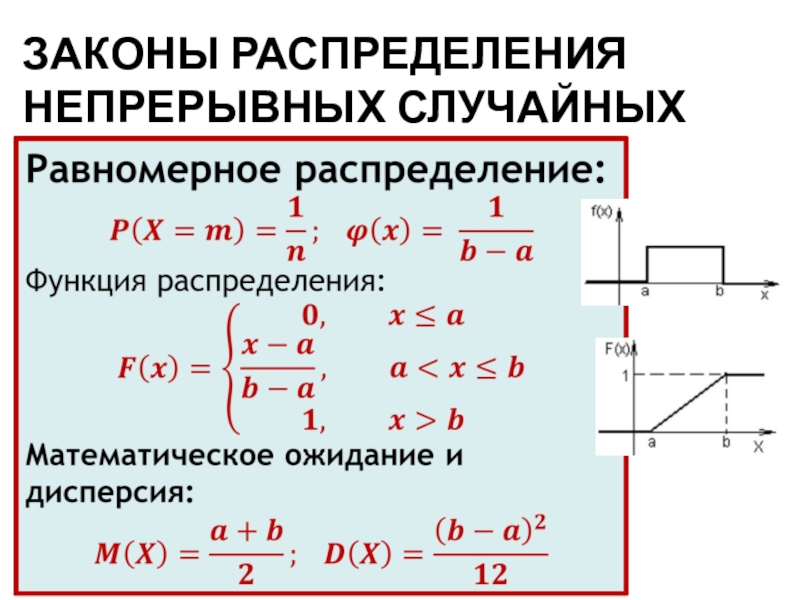
- 22. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
- 23. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
- 24. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
- 25. Показательное (экспоненциальное) распределение.Основные характеристики (математическое ожидание и
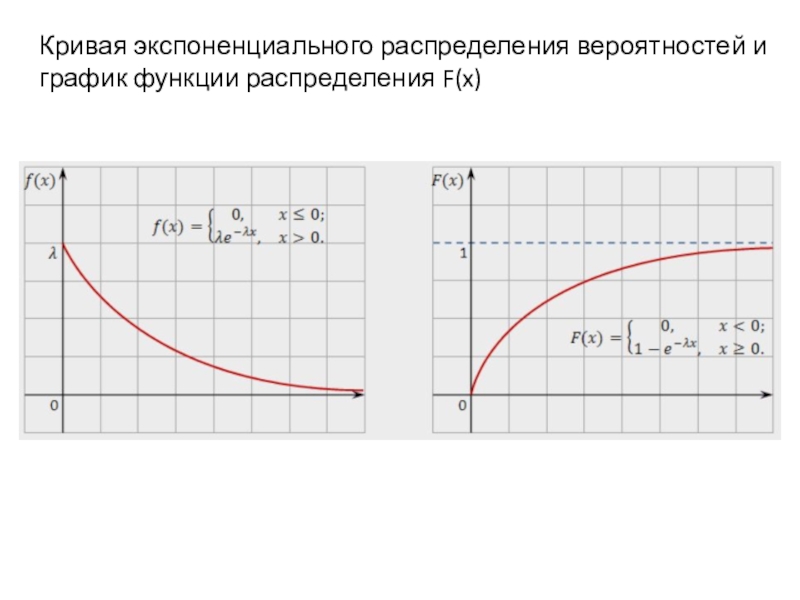
- 26. Кривая экспоненциального распределения вероятностей и график функции распределения F(x)
- 27. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
- 28. Нормальное распределение.Плотность вероятности нормально распределённой случайной величины X выражается формулой:ЗАКОНЫ РАСПРЕДЕЛЕНИЯ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
- 29. Слайд 29
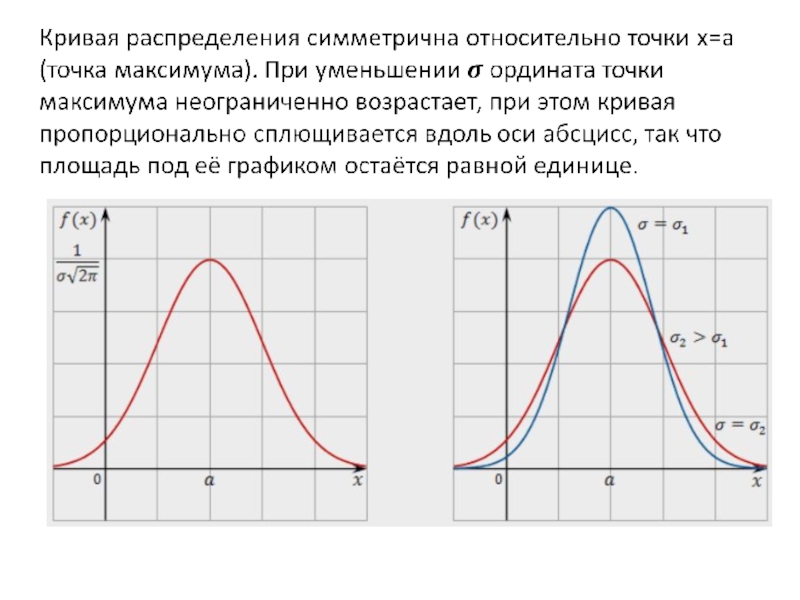
- 30. Нормальный закон распределения широко применяется в задачах
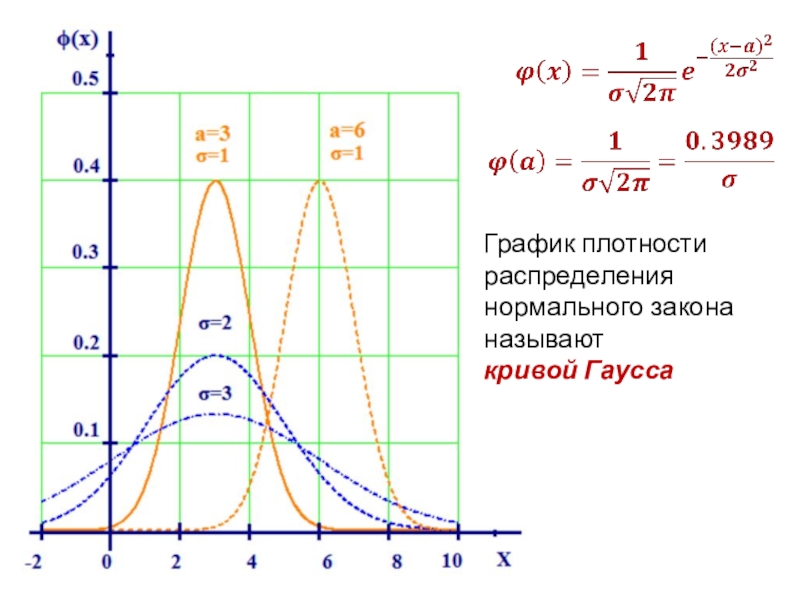
- 31. График плотности распределения нормального закона называюткривой Гаусса
- 32. Слайд 32
- 33. Слайд 33
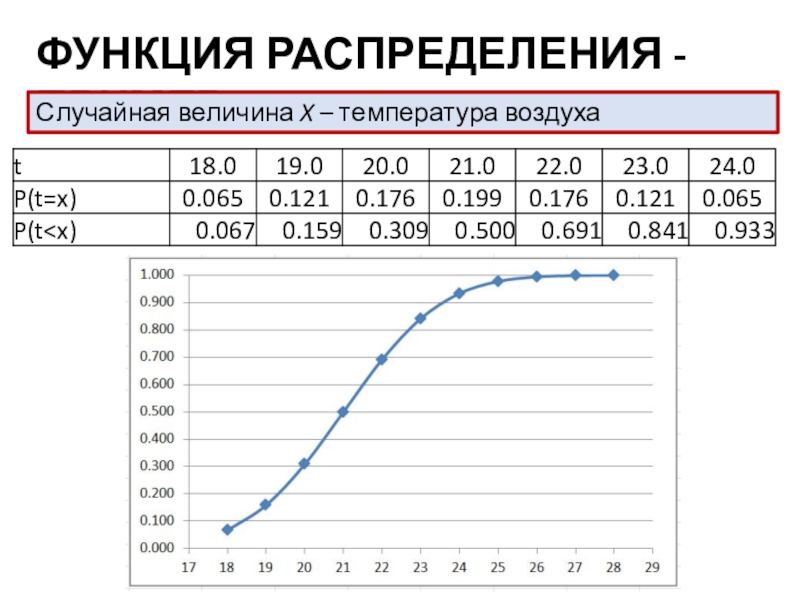
- 34. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ - ПРИМЕРСлучайная величина X – температура воздуха
- 35. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
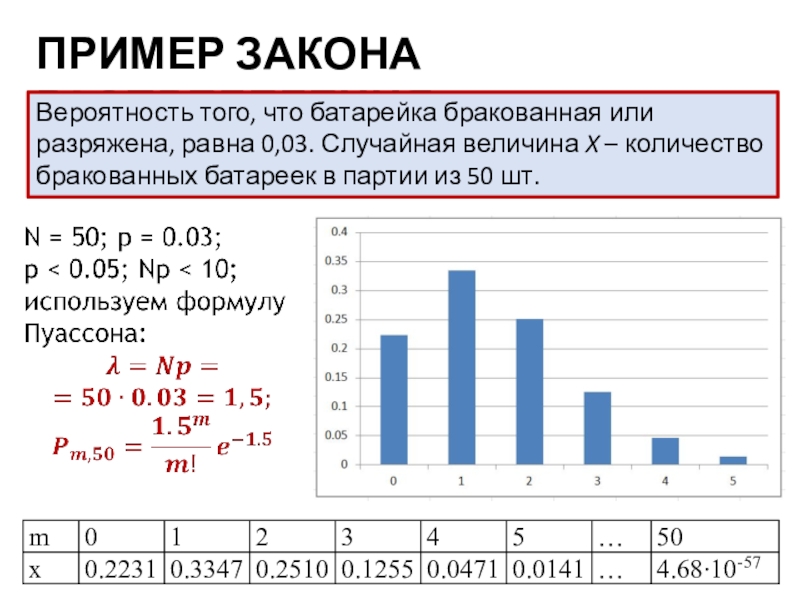
- 36. ПРИМЕР ЗАКОНА РАСПРЕДЕЛЕНИЯВероятность того, что батарейка бракованная
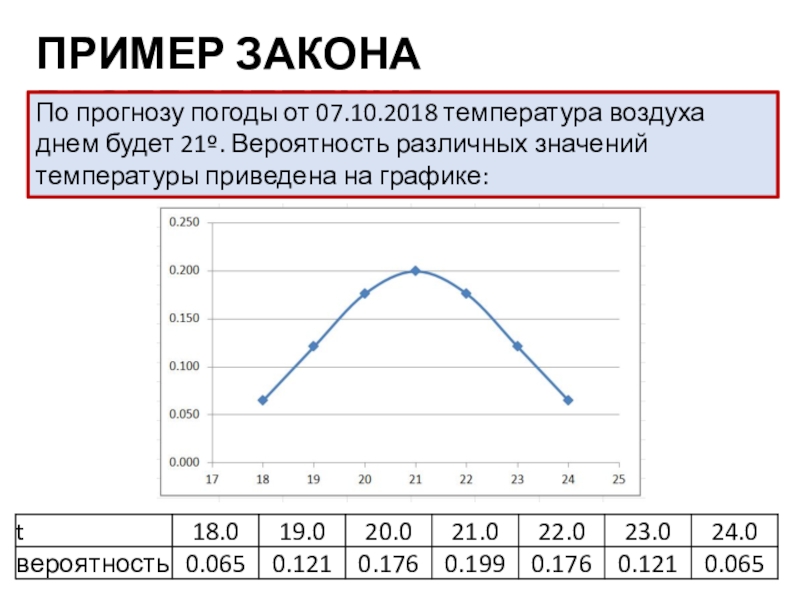
- 37. ПРИМЕР ЗАКОНА РАСПРЕДЕЛЕНИЯ - 2По прогнозу погоды
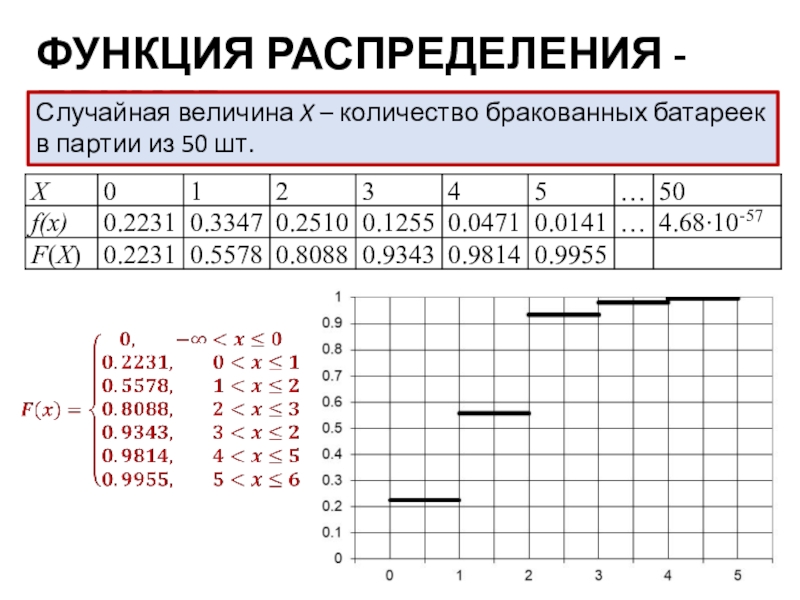
- 38. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ - ПРИМЕРСлучайная величина X – количество бракованных батареек в партии из 50 шт.
- 39. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ - ПРИМЕР
- 40. ДИСПЕРСИЯ - ПРИМЕР
- 41. ДИСПЕРСИЯ – ПРИМЕР РАСЧЕТАM(X)=0∙0.2231 + 1∙0.3347 +
- 42. Законы распределения дискретных случайных величин1. Биномиальное распределение2. Распределение Пуассона3. Геометрическое распределение
- 43. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
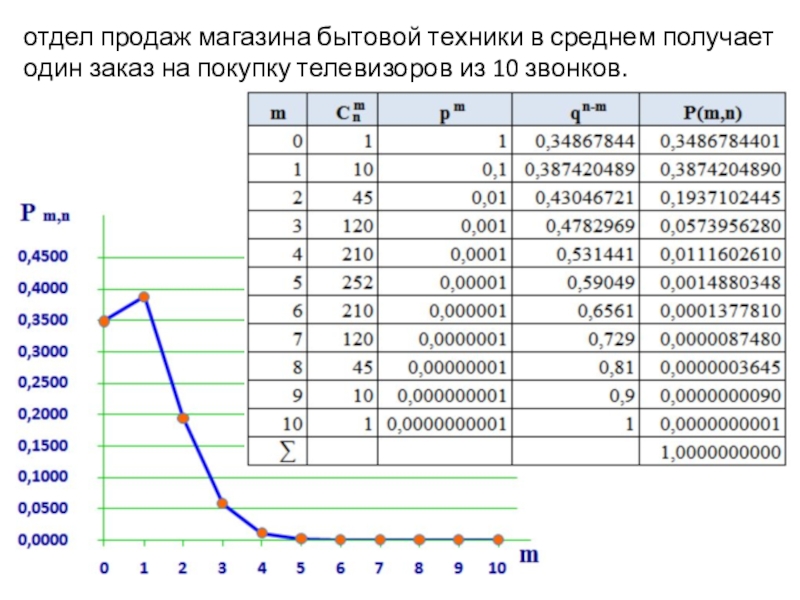
- 44. отдел продаж магазина бытовой техники в среднем
- 45. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
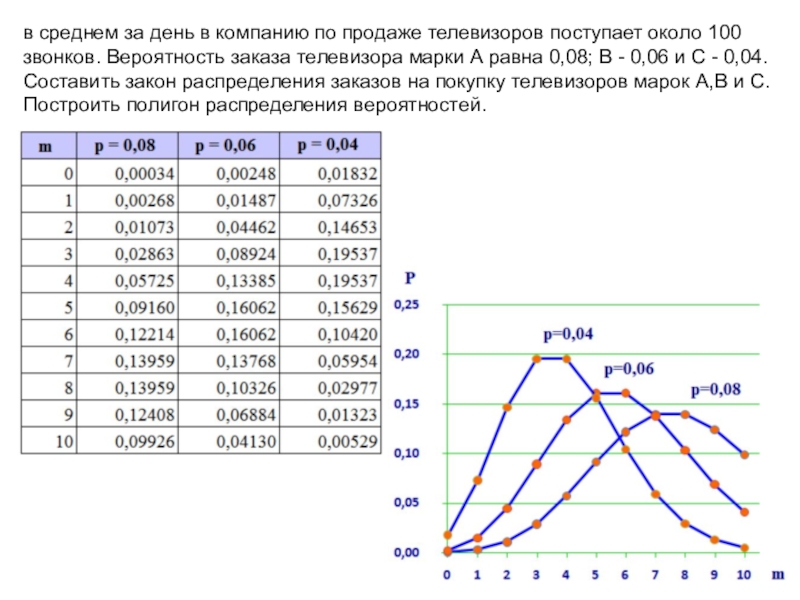
- 46. в среднем за день в компанию по
- 47. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
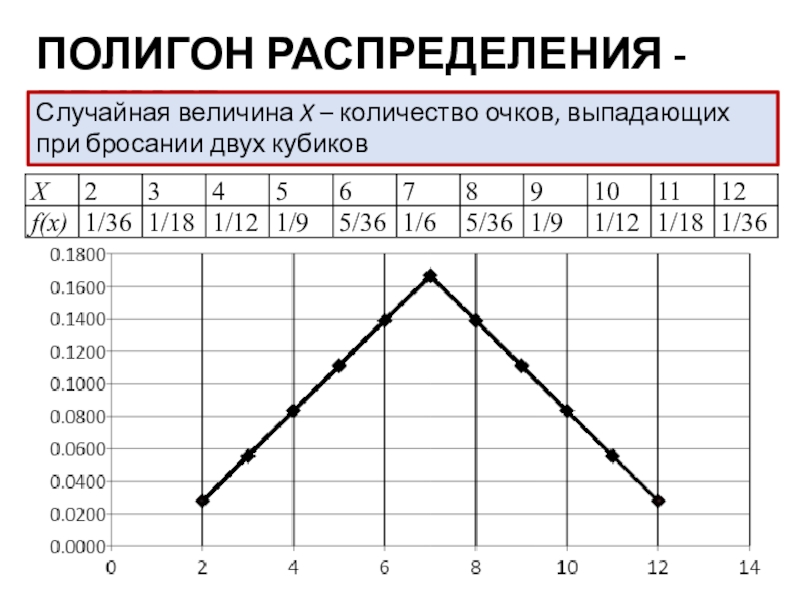
- 48. В компанию по ремонту бытовой техники поступила
- 49. Скачать презентанцию
ЧТО НУЖНО ВСПОМНИТЬ:переменная, которая в зависимости от исхода опыта, т.е. в зависимости от случая, принимает различные значения.Случайная величина Х называется
Слайды и текст этой презентации
Слайд 1Законы распределения случайных величин
1. Понятие закона распределения.
2. Законы распределения дискретных
случайных величин.
построения компьютерных сетей, занятие 20
Слайд 2ЧТО НУЖНО ВСПОМНИТЬ:
переменная, которая в зависимости от исхода опыта, т.е.
в зависимости от случая, принимает различные значения.
Случайная величина Х называется
, если она может принимать только конечное или счетное множество значенийесли она может принимать любые значения из некоторого конечного или бесконечного интервала.
Случайная величина – это . . .
дискретной
Случайная величина называется непрерывной,
Слайд 3ЗАКОН РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
Случайная величина считается заданной, если для каждого
возможного ее значения известна (задана) вероятность этого значения
Формы закона распределения
случайной величины:ряд распределения;
функция распределения;
функция плотности вероятности
это соответствие между значением случайной величины и вероятностью этого значения
Закон распределения случайной величины –
Слайд 4РЯД РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
Ряд распределения – это таблица, где перечислены
возможные значения случайной величины и соответствующие им вероятности.
Эта форма
закона распределения используется только для дискретных случайных величинГрафическим изображением ряда распределения является полигон (многоугольник) распределения
Слайд 5ПОЛИГОН РАСПРЕДЕЛЕНИЯ - ПРИМЕР
Случайная величина X – количество очков, выпадающих
при бросании двух кубиков
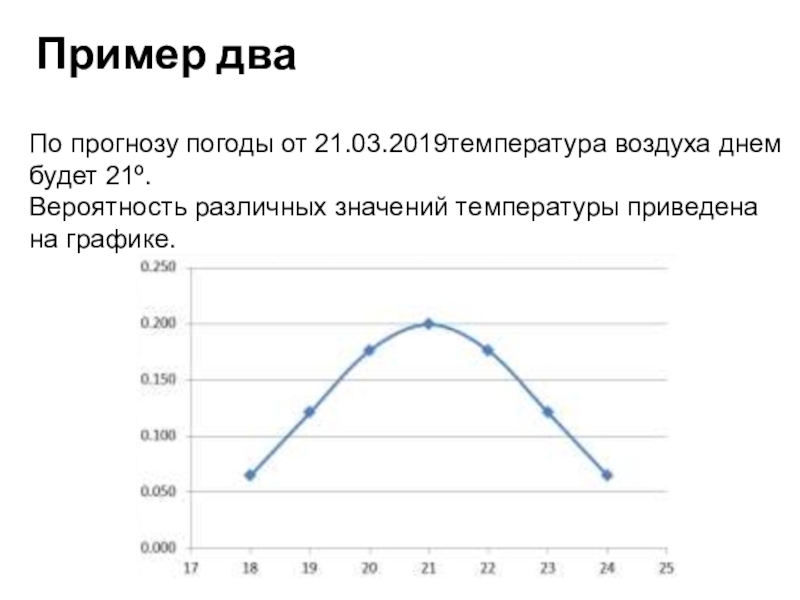
Слайд 6Пример два
По прогнозу погоды от 21.03.2019температура воздуха днем будет 21º.
Вероятность различных значений температуры приведена на графике.
Слайд 7Пример два
Температура воздуха – непрерывная случайная величина.
Закон распределения дискретной величины
может быть задан в табличной форме.
Однако для многих случайных
величин имеется и функциональное соответствие между значениями и вероятностями–функция плотности распределения.
Слайд 9ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ - ПРИМЕР
Случайная величина X – количество очков, выпадающих
при бросании двух кубиков
Слайд 14ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
математическое ожидание,
дисперсия,
моменты различных порядков,
мода
и
медиана.
Слайд 15МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ
M(X)=0∙0.2231 + 1∙0.3347 + 2∙0.2510 + 3∙0.1255 +
+ 4∙0.0471 + 5 ∙0.0186 = 1.4946
Слайд 16СВОЙСТВА МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ
1. Математическое ожидание суммы двух случайных величин равно
сумме их математических ожиданий:
M(X+Y) = M(X) + M(Y)
2. Математическое ожидание
произведения двух независимых случайных величин равно произведению их математических ожиданий: M(X·Y) = M(X) · M(Y)3. Математическое ожидание постоянной величины равно значению постоянной. Постоянную можно выносить за знак математического ожидания: M(c) = c; M(cX) = c·M(X)
4. Математическое ожидание отклонения случайной величины от математического ожидания равно нулю:
M(x - M(X)) = 0
Слайд 17ДИСПЕРСИЯ
Дисперсией называют математическое ожидание квадрата отклонения случайной величины от ее
математического ожидания:
D(X) = M((X – M(X))2)
Слайд 19Законы распределения непрерывных случайных величин
1. Равномерное распределение
2. Показательное (экспоненциальное) распределение
3.
Нормальное распределение
Слайд 21Равномерное распределение.
Непрерывная случайная величина имеет равномерное распределение на отрезке [a,
b], если на этом отрезке плотность распределения случайной величины постоянна,
а вне его равна нулю.Постоянная величина С может быть определена из условия равенства единице площади, ограниченной кривой распределения.
ЗАКОНЫ РАСПРЕДЕЛЕНИЯ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
![Равномерное распределение.Непрерывная случайная величина имеет равномерное распределение на отрезке [a, b], если на этом отрезке плотность распределения](/img/tmb/6/505268/0eacb61baa22aa04a5ec3eae9f794105-800x.jpg "Законы распределения случайных величин Равномерное распределение.Непрерывная случайная величина имеет равномерное распределение на отрезке [a, b],")
Слайд 25Показательное (экспоненциальное) распределение.
Основные характеристики (математическое ожидание и дисперсия) случайной величины
X, распределённой по экспоненциальному, имеют вид:
ЗАКОНЫ РАСПРЕДЕЛЕНИЯ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
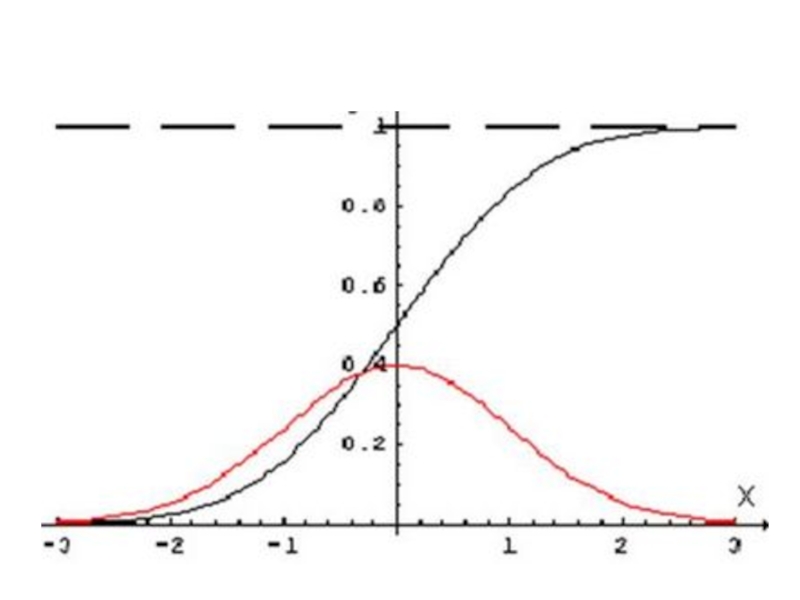
Слайд 28Нормальное распределение.
Плотность вероятности нормально распределённой случайной величины X выражается формулой:
ЗАКОНЫ
РАСПРЕДЕЛЕНИЯ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
Слайд 30Нормальный закон распределения широко применяется в задачах практики.
Объяснить причины
этого впервые удалось Ляпунову.
Он показал, что если случайная величина
может рассматриваться как сумма большого числа малых слагаемых, то при достаточно общих условиях закон распределения этой случайной величины близок к нормальному независимо от того, каковы законы распределения отдельных слагаемых. А так как практически случайные величины в большинстве случаев бывают результатом действия множества причин, то нормальный закон оказывается наиболее распространённым законом распределения.
Слайд 36ПРИМЕР ЗАКОНА РАСПРЕДЕЛЕНИЯ
Вероятность того, что батарейка бракованная или разряжена, равна
0,03. Случайная величина X – количество бракованных батареек в партии
из 50 шт.
Слайд 37ПРИМЕР ЗАКОНА РАСПРЕДЕЛЕНИЯ - 2
По прогнозу погоды от 07.10.2018 температура
воздуха днем будет 21º. Вероятность различных значений температуры приведена на
графике:
Слайд 38ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ - ПРИМЕР
Случайная величина X – количество бракованных батареек
в партии из 50 шт.
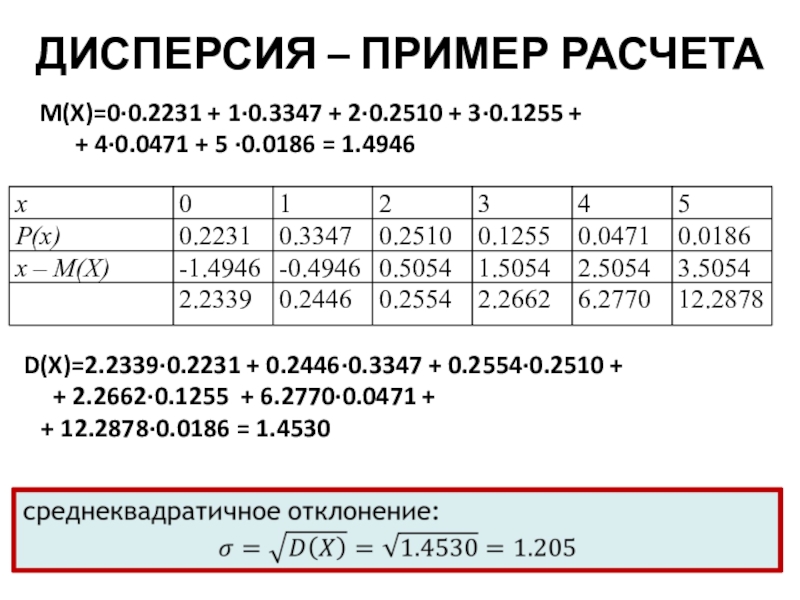
Слайд 41ДИСПЕРСИЯ – ПРИМЕР РАСЧЕТА
M(X)=0∙0.2231 + 1∙0.3347 + 2∙0.2510 + 3∙0.1255
+
+ 4∙0.0471 + 5 ∙0.0186 = 1.4946
D(X)=2.2339∙0.2231 + 0.2446∙0.3347 + 0.2554∙0.2510 +
+ 2.2662∙0.1255 + 6.2770∙0.0471 +
+ 12.2878∙0.0186 = 1.4530
Слайд 42Законы распределения дискретных случайных величин
1. Биномиальное распределение
2. Распределение Пуассона
3. Геометрическое
распределение
Слайд 44отдел продаж магазина бытовой техники в среднем получает один заказ
на покупку телевизоров из 10 звонков.
Слайд 46в среднем за день в компанию по продаже телевизоров поступает
около 100 звонков. Вероятность заказа телевизора марки А равна 0,08;
B - 0,06 и C - 0,04. Составить закон распределения заказов на покупку телевизоров марок А,В и С. Построить полигон распределения вероятностей.
Слайд 48В компанию по ремонту бытовой техники поступила партия из 10
запасных блоков. Бывают случаи, что в партии оказывается 1 блок
бракованный. Проводится проверка до обнаружения бракованного блока.
