Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Функции и их графики
Содержание
- 1. Функции и их графики
- 2. Экстремумы функции. Наибольшее и наименьшее значение функцииСодержаниеПонятие функцииОбщие свойства функцииПонятие обратной функцииНепрерывностьЭлементарные функцииВведение
- 3. При изучении явлений окружающего мира и
- 4. Понятие функции Пусть D и E –
- 5. Общие свойства функцииЧетность и нечетностьна главнуюПериодичностьНули функцииПромежутки знакопостоянстваМонотонность
- 6. Четность и нечетность Определение: Функция y =
- 7. Определение: Функция y = f(x) называется
- 8. При построении графиков четной и нечетной
- 9. Периодичность Определение: Функция y = f(x) называется
- 10. Число T называется периодом функции. Всякая
- 11. Нули функцииОпределение: Нулем функции называется такое действительное
- 12. Промежутки знакопостоянстваОпределение: Числовые промежутки, на которых непрерывная
- 13. МонотонностьФункцию называют монотонно возрастающей, если с увеличением
- 14. Определение: Функция y = f(x) называется монотонно
- 15. Понятие обратной функции Функция, принимающая каждое свое
- 16. Экстремумы функции. Наибольшее и наименьшее значение функции
- 17. Определение 1. Пусть функция y = f(x)
- 18. Определение 2. Пусть функция y = f(x)
- 19. Непрерывность Функция y = f(x) называется непрерывной
- 20. Элементарные функцииЛинейнаяОбратная пропорциональностьКвадратичнаяСтепеннаяПоказательнаяЛогарифмическаяТригонометрическиена главную
- 21. Линейная функцияОпределение: Функция вида y = kx
- 22. 2. Если b = 0, то y
- 23. 3. Если k ≠ 0 и b
- 24. Коэффициенты k и b в уравнении линейной
- 25. Обратная пропорциональностьОпределение: Функция вида x = k/x,
- 26. График обратной пропорциональности называется гиперболой. Участки кривой
- 27. Квадратичная функцияОпределение: Функция вида y = ax2
- 28. 2. Квадратичная функция вида y = ax2
- 29. 3. Квадратичная функция общего вида y =
- 30. Если он равен нулю, то график функции
- 31. Степенная функцияОпределение: Функция, заданная формулой y =
- 32. Показательная функцияОпределение: Функция, которую можно задать формулой
- 33. Логарифмическая функцияОпределение: Функция вида y = logax,
- 34. Тригонометрические функции 1.Функция синус. Определение:
- 35. 2.Функция косинус.Определение: Числовая функция, заданная формулой
- 36. 3.Функция тангенс.Определение: Числовая функция, заданная формулой
- 37. 4.Функция котангенс.Определение: Числовая функция, заданная формулой
- 38. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Экстремумы функции. Наибольшее и наименьшее значение функции
Содержание
Понятие функции
Общие свойства функции
Понятие
обратной функции
Слайд 3 При изучении явлений окружающего мира и в практической деятельности
нам приходится рассматривать величины различной природы: длину, площадь, объём, массу,
температуру, время и т. д. В зависимости от рассматриваемых условий одни из величин имеют постоянные числовые значения, у других эти значения переменные. Такие величины соответственно называются постоянными и переменными.Математика изучает зависимость между переменными в процессе их изменения. Например, при изменении радиуса круга меняется и его площадь, и мы рассматриваем вопрос об изменении площади круга в зависимости от изменения его радиуса.
Математическим выражением взаимной связи реальных величин является идея функциональной зависимости. Понятие функции – важнейшее понятие математики. Слово «функция» (от латинского «Functio» - исполнение обязанностей, деятельность) впервые ввел немецкий ученый Г. Лейбниц.
Введение
на главную
Слайд 4Понятие функции
Пусть D и E – непустые числовые множества,
а x и y – соответственно их элементы. Если каждому
x∈D (x принадлежит множеству D) ставится, в соответствии с некоторым законом, только одно значение y∈E, то говорят, что между переменными x и y существует функциональная зависимость, и x называют независимой переменной (или аргументом), а y – зависимой переменной (или функцией).Символическая запись функции: y = f(x) (x∈D, y∈E). Множество D называют областью определения функции и обозначают D(f), а множество E называют областью изменения функции – E(f). Говорят еще, что функция f отображает множество D на множестве E.
на главную
Слайд 5Общие свойства функции
Четность и нечетность
на главную
Периодичность
Нули функции
Промежутки знакопостоянства
Монотонность
Слайд 6Четность и нечетность
Определение: Функция y = f(x) называется четной,
если для любого значения x, взятого из области определения функции,
значение –x также принадлежит области определения и выполняется равенство f(-x) = f(x).Примеры четных функций:
y = x2; y = x2 + 5; y = -3x2 + 1; y = ½x½; y = 3.
(y = x2; y(1) = 12 = 1; y(-1) = (-1)2 = 1; y(1) = y(-1)).
Согласно определению, четная функция определена на множестве, симметричном относительно начала координат.
График четной функции симметричен относительно оси ординат:
y
x
O
x0
- x0
назад
далее
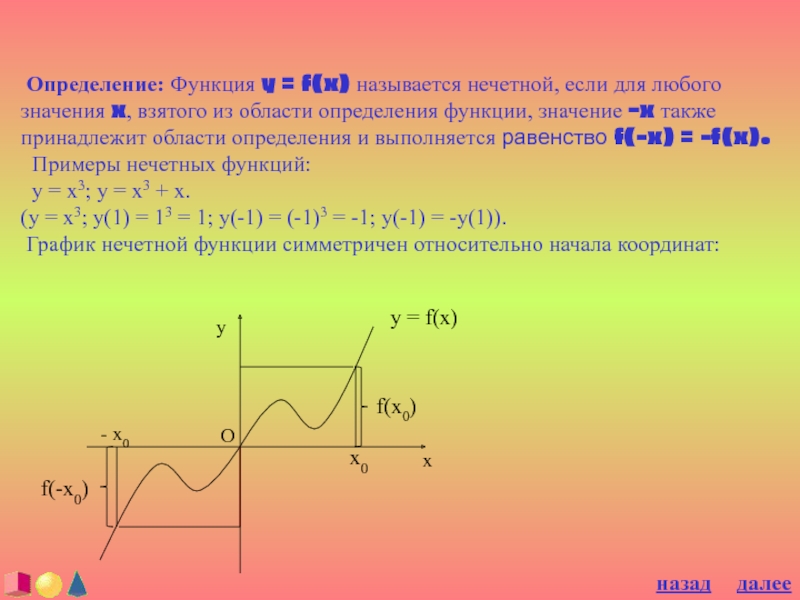
Слайд 7 Определение: Функция y = f(x) называется нечетной, если для
любого значения x, взятого из области определения функции, значение –x
также принадлежит области определения и выполняется равенство f(-x) = -f(x).Примеры нечетных функций:
y = x3; y = x3 + x.
(y = x3; y(1) = 13 = 1; y(-1) = (-1)3 = -1; y(-1) = -y(1)).
График нечетной функции симметричен относительно начала координат:
f(-x0)
O
y = f(x)
далее
назад
Слайд 8
При построении графиков четной и нечетной функции достаточно построить
только правую ветвь графика для положительных значений аргумента. Левая ветвь
достраивается симметрично относительно начала координат для нечетной функции и относительно оси ординат для четной функции.Произведение двух четных или двух нечетных функций представляет собой четную функцию, а произведение четной и нечетной функций – нечетную функцию.
Конечно, большинство функций не являются ни четными, ни нечетными.
Пример:
y = x3 + x2
y(-1) = (-1)3 + (-1)2 = -1 + 1 = 0
y(1) = (1)3 + (1)2 = 1 + 1 = 2
назад
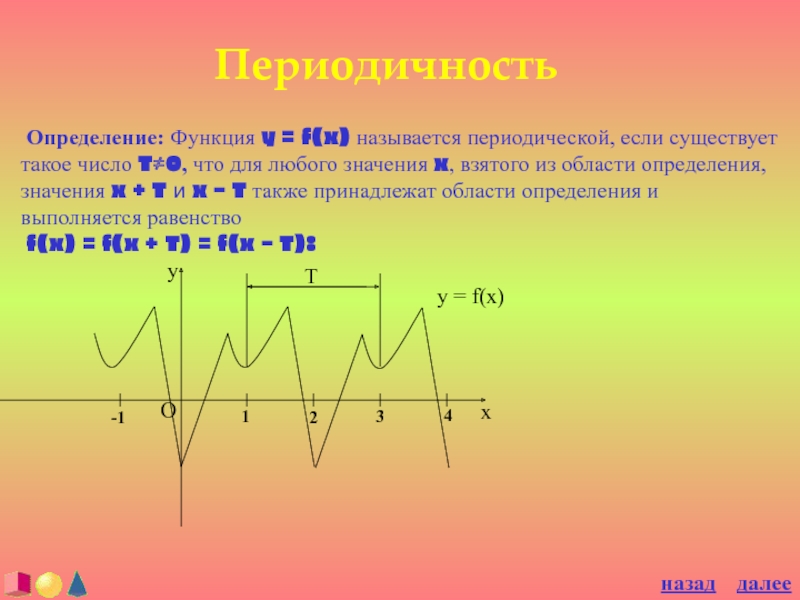
Слайд 9Периодичность
Определение: Функция y = f(x) называется периодической, если существует
такое число T≠0, что для любого значения x, взятого из
области определения, значения x + T и x – T также принадлежат области определения и выполняется равенствоf(x) = f(x + T) = f(x – T):
y
1
2
4
3
-1
T
y = f(x)
далее
назад
Слайд 10 Число T называется периодом функции. Всякая периодическая функция имеет
бесконечное число периодов.В самом деле, числа вида nT при любом
целом n также являются периодом функции f(x), так как f(x + nT) = f(x + (n - 1)T + T) = f(x + (n – 1)T) = f(x + (n - 2)T + T) = f(x + (n - 2)T) = … = f(x).Иногда периодом называют наименьшее их всех чисел T > 0, удовлетворяющее данному выше определению. Примеры периодических функций:
y = sin x; y = ctg x; y = sin3x.
Периодической является и всякая постоянная функция, причем ее периодом служит любое ненулевое число. Например: y = 2; y = 10.
назад
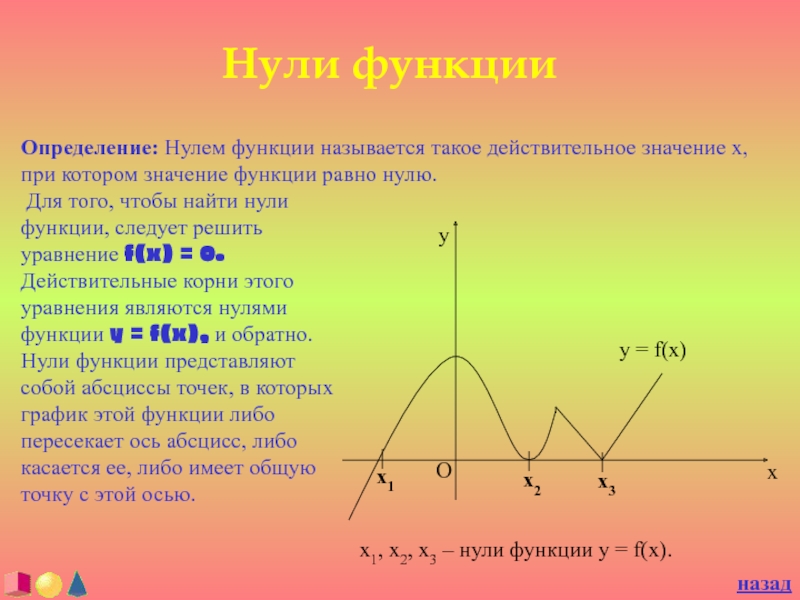
Слайд 11Нули функции
Определение: Нулем функции называется такое действительное значение x, при
котором значение функции равно нулю.
назад
Для того, чтобы найти нули
функции, следует решить уравнение f(x) = 0. Действительные корни этого уравнения являются нулями функции y = f(x), и обратно. Нули функции представляют собой абсциссы точек, в которых график этой функции либо пересекает ось абсцисс, либо касается ее, либо имеет общую точку с этой осью.х1, х2, х3 – нули функции у = f(x).
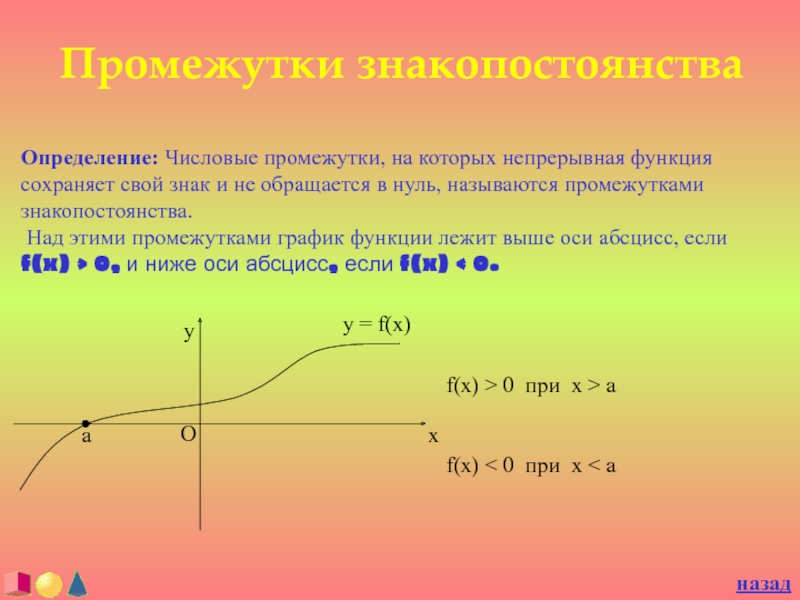
Слайд 12Промежутки знакопостоянства
Определение: Числовые промежутки, на которых непрерывная функция сохраняет свой
знак и не обращается в нуль, называются промежутками знакопостоянства.
Над
этими промежутками график функции лежит выше оси абсцисс, если f(x) > 0, и ниже оси абсцисс, если f(x) < 0.назад
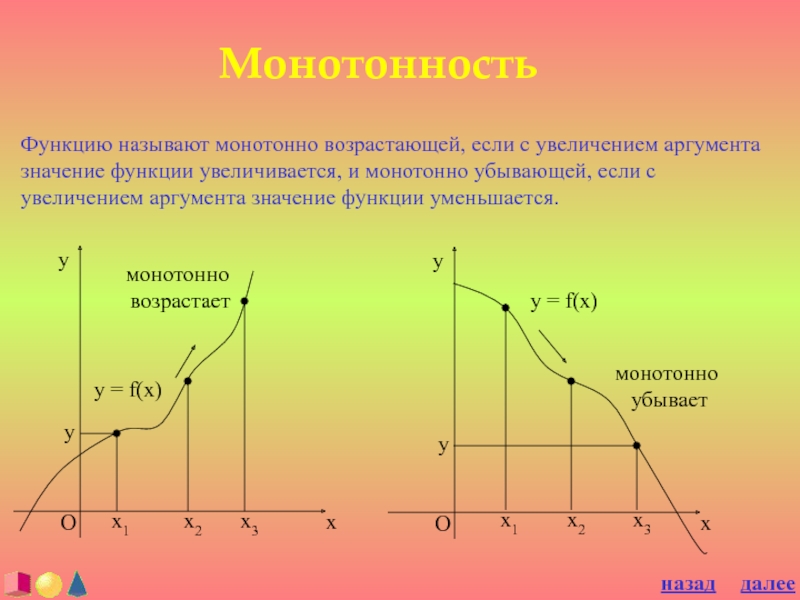
Слайд 13Монотонность
Функцию называют монотонно возрастающей, если с увеличением аргумента значение функции
увеличивается, и монотонно убывающей, если с увеличением аргумента значение функции
уменьшается.y = f(x)
далее
назад
Слайд 14Определение: Функция y = f(x) называется монотонно возрастающей на интервале
(a, b), если для любых x1 и x2, принадлежащих этому
интервалу, из неравенства x2 > x1 следует неравенство f(x2) > f(x1). Функция y = f(x) называется монотонно убывающей на интервале (a, b), если для любых x1 и x2, принадлежащих этому интервалу, из неравенства x2 > x1 следует неравенство f(x2) < f(x1). Интервал (a, b) предполагает взятым из области определения функции.назад
Слайд 15Понятие обратной функции
Функция, принимающая каждое свое значение в единственной
точке области определения, называется обратимой. Таким образом, при k≠0 функция
f(x) = kx + b обратима, а функция f(x) = x2 не является обратимой.Если между величинами х и у существует функциональная зависимость, то, вообще говоря, безразлично, какую из этих величин считать аргументом, а какую – функцией.
Пусть задана функция y = f(x), где y является зависимой переменной, x – аргументом. Очевидно, в этом случае x и y можно поменять ролями, т. е. x будет функцией, а y – аргументом. Тогда рассматриваемая функциональная зависимость между x и y запишется так: x = Y(y). Функция x = Y(y) называется обратной по отношению к функции y = f(x).
на главную
y
x
O
1
-1
−π
π
π/2
−π/2
y = sin x
Слайд 16Экстремумы функции. Наибольшее и наименьшее значение функции
Точка x0 называется
точкой максимума (точкой минимума) для функции f(x), если значение в
этой точке больше (меньше), чем значение функции в ближайших соседних точках.для обозначения максимума и минимума существует общий термин «экстремум» (от латинского «крайний»).
далее
на главную
Слайд 17Определение 1. Пусть функция y = f(x) определена на отрезке[a;
b]. Говорят, что функция имеет максимум в точке x0∈ [a;
b], если существует окрестность точки x0, целиком содержащаяся в [a; b] и такая, что для любого x, принадлежащего этой окрестности, выполняется неравенство f(x) < f(x0).Под окрестностью точки x0 понимают интервал длины 2e с центром в точке x0, т. е. (x0 – e ; x0 + e), где e – произвольное положительное число.
далее
назад
Слайд 18Определение 2. Пусть функция y = f(x) определена на отрезке
[a; b]. Говорят, что функция имеет минимум в точке x0∈
[a; b], если существует окрестность точки x0, целиком содержащаяся в [a; b] и такая, что для любого x, принадлежащего этой окрестности, выполняется неравенство f(x) > f(x0).Максимумы и минимумы функции не являются обязательно наибольшими и наименьшими значениями этой функции во всей области определения. Например, функция y = f(x) определена на отрезке [a; b], имеет четыре экстремума: два минимума (x = C1 и x = C3) и два максимума (x = C2 и x = C4). Вместе с тем, функция достигает наибольшего значения при x = a и наименьшего при x = b.
Признак максимума функции:
Если функция непрерывна в точке x0
и ее производная, переходя через нее,
меняет знак с плюса на минус,
то x0 есть точка максимума.
Признак минимума функции:
Если функция непрерывна в точке x0
и ее производная, переходя через нее,
меняет знак с минуса на плюс, то x0 есть точка
минимума.
назад
Слайд 19Непрерывность
Функция y = f(x) называется непрерывной на промежутке, если
она определена на этом промежутке и непрерывна в каждой точке
промежутка.Геометрическая непрерывность функции на промежутке означает, что график этой функции на данном промежутке изображен сплошной линией без скачков и разрывов. При этом малому изменению аргумента соответствует малое изменение функции.
Если при x = a функция y = f(x) существует в окрестности этой точки, но в самой точке x = a не выполняется условие непрерывности, говорят, что точка x = a есть точка разрыва функции. В самой точке x = a функция может существовать, а может и не существовать.
на главную
Слайд 20Элементарные функции
Линейная
Обратная пропорциональность
Квадратичная
Степенная
Показательная
Логарифмическая
Тригонометрические
на главную
Слайд 21Линейная функция
Определение: Функция вида y = kx + b, где
k и b некоторые числа, называется линейной функцией.
1. Если
k = 0, тогда y = b.Эта функция определена на множестве R и для каждого X принимает одно и то же значение, равное b.
Графиком является прямая, параллельная оси Оx и отстоящая от нее на ⏐b⏐ единиц вверх, если b > 0, и вниз, если b < 0; если b = 0, то прямая совпадает с осью Ox.
далее
назад
Слайд 222. Если b = 0, то y = kx.
Линейная
функция вида y = kx называется прямой пропорциональностью. Она определена
на множестве R. Функция является монотонно возрастающей, если k > 0, и монотонно убывающей, если k < 0. Графиком функции является прямая, проходящая через начало координат. При k > 0 точки графика принадлежат I и III координатным четвертям. При k < 0 точки графика принадлежат II и IV координатным четвертям.O
y
x
y = kx
k < 0
назад
далее
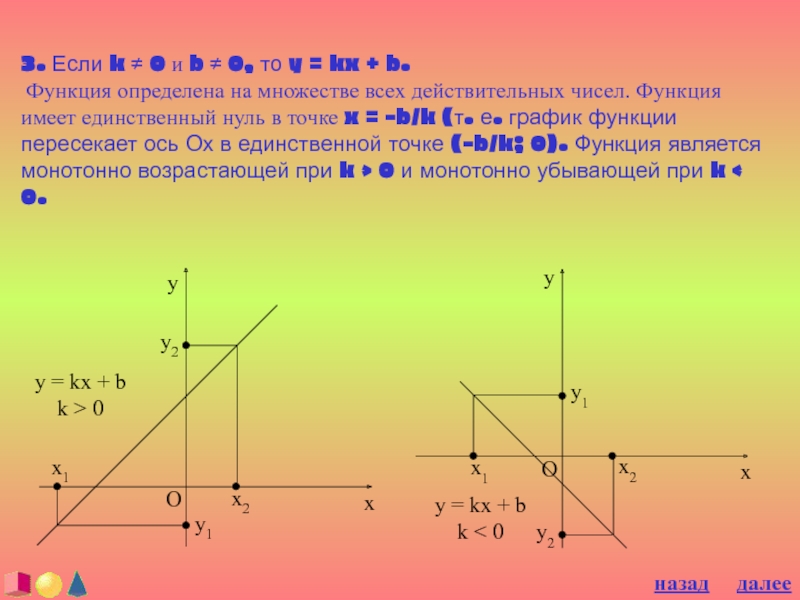
Слайд 233. Если k ≠ 0 и b ≠ 0, то
y = kx + b.
Функция определена на множестве всех
действительных чисел. Функция имеет единственный нуль в точке x = -b/k (т. е. график функции пересекает ось Ох в единственной точке (-b/k; 0). Функция является монотонно возрастающей при k > 0 и монотонно убывающей при k < 0. назад
далее
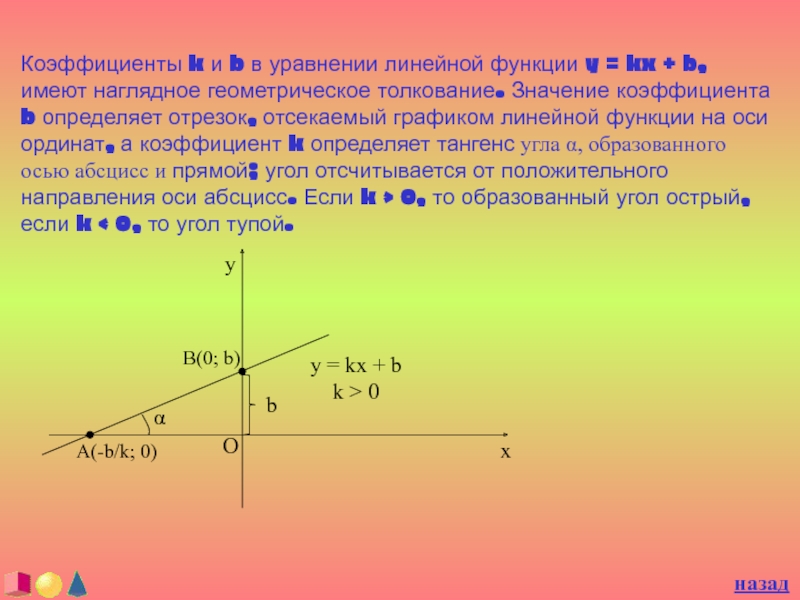
Слайд 24Коэффициенты k и b в уравнении линейной функции y =
kx + b, имеют наглядное геометрическое толкование. Значение коэффициента b
определяет отрезок, отсекаемый графиком линейной функции на оси ординат, а коэффициент k определяет тангенс угла α, образованного осью абсцисс и прямой; угол отсчитывается от положительного направления оси абсцисс. Если k > 0, то образованный угол острый, если k < 0, то угол тупой.назад
Слайд 25Обратная пропорциональность
Определение: Функция вида x = k/x, k ≠ 0,
называется обратной пропорциональностью.
Область определения этой функции совпадает с ее
областью значений и представляет собой объединение двух промежутков: (-∞; 0) ∪ (0; + ∞). Функция не имеет нулей, так как уравнение k/x = 0 не имеет корней.
Если k > 0 , то функция монотонно убывает на всей области определения. Если k < 0, то функция монотонно возрастает на всей области определения функции.
далее
назад
y = k / x
k > 0
y = k / x
k < 0
Слайд 26График обратной пропорциональности называется гиперболой. Участки кривой при x >
0 и x < 0 называются ветвями гиперболы.
назад
Слайд 27Квадратичная функция
Определение: Функция вида y = ax2 + bx +
c, где a, b,c – некоторые числа, a ≠ 0,
называется квадратичной.1. Функция вида y = x2 – простейшая квадратичная функция. Это четная функция, у которой D = (-∞; + ∞), а E = [0; + ∞). При x > 0 она возрастающая, а при x < 0 - убывающая. Ее график называется параболой. График проходит через начало координат, симметричен относительно оси ординат, ветви параболы направлены вверх.
назад
далее
Слайд 282. Квадратичная функция вида y = ax2 также четная, неограниченная,
определенная для всех действительных x. Ее график также парабола, проходящая
через начало координат и симметричная относительно оси ординат. Но при a > 0 ветви ее направлены вверх и E = [0; + ∞), а при a < 0 ветви направлены вниз и E = (-∞; 0). Чем меньше абсолютная величина a, тем дальше отходят ветви параболы от оси ординат, тем «шире» она. Чем больше абсолютная величина a, тем плотнее ветви параболы прижаты к оси ординат, тем «уже» она.назад
далее
Слайд 293. Квадратичная функция общего вида y = ax2 + bx
+ c также четная, неограниченная, определенная для всех действительных x.
Ее график – парабола, симметричная относительно прямой x = x0 (x0 – абсцисса вершины параболы), параллельной оси ординат. Если a > 0, то ее ветви направлены вверх и E = [y0; + ∞) или вниз при a < 0 и тогда E = (-∞; y0), где y0 – ордината вершины параболы. Только вершина этой параболы находится не в начале координат, а в точке (-b / 2a; (4ac- b2) / 4a). Парабола пересекает ось ординат в точке (0; c). Если дискриминант квадратного трехчлена ax2 + bx + c отрицательный, т. е. B2 – 4ac < 0, то график функции y = ax2 + bx + c не пересекает ось абсцисс.назад
далее
y = ax2 + bx +c
a < 0
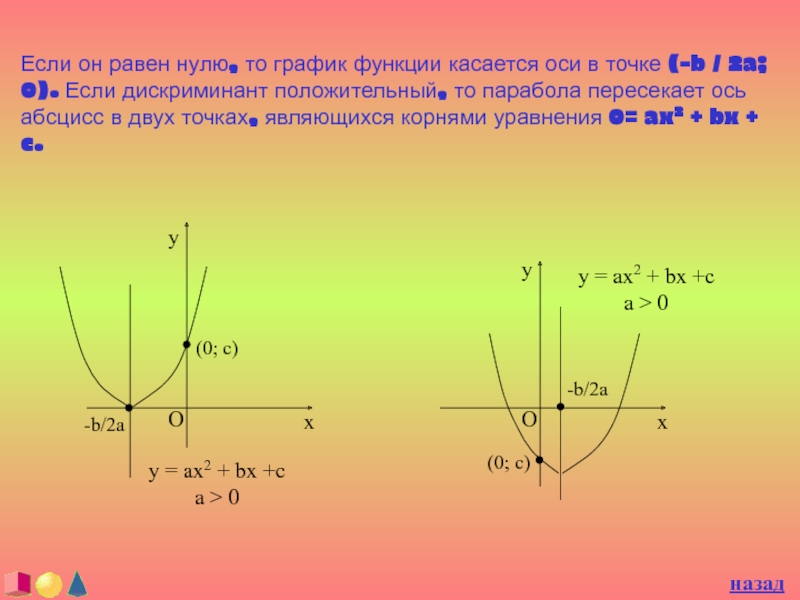
Слайд 30Если он равен нулю, то график функции касается оси в
точке (-b / 2a; 0). Если дискриминант положительный, то парабола
пересекает ось абсцисс в двух точках, являющихся корнями уравнения 0= ax2 + bx + c.назад
Слайд 31Степенная функция
Определение: Функция, заданная формулой y = xn , называется
степенной.
1. При n, равном 1; 2; -1, имеем соответственно
функции y = x, y = x2; y = -1 / x, уже рассмотренные ранее.2. Если n – число целое и четное, то функция y = xn – четная; при нечетном n она нечетная. При положительных n эта функция определена для всех действительных значений аргумента x, при отрицательных n она определена для всех x, кроме x = 0.
При любом n ≠ 0 степенная функция неограниченная, график каждой из них проходит через точку (1; 1).
Если n – число иррациональное, то функция y = xn определена только для положительных значений аргумента x или для неотрицательных x, если n > 0.
назад
Слайд 32Показательная функция
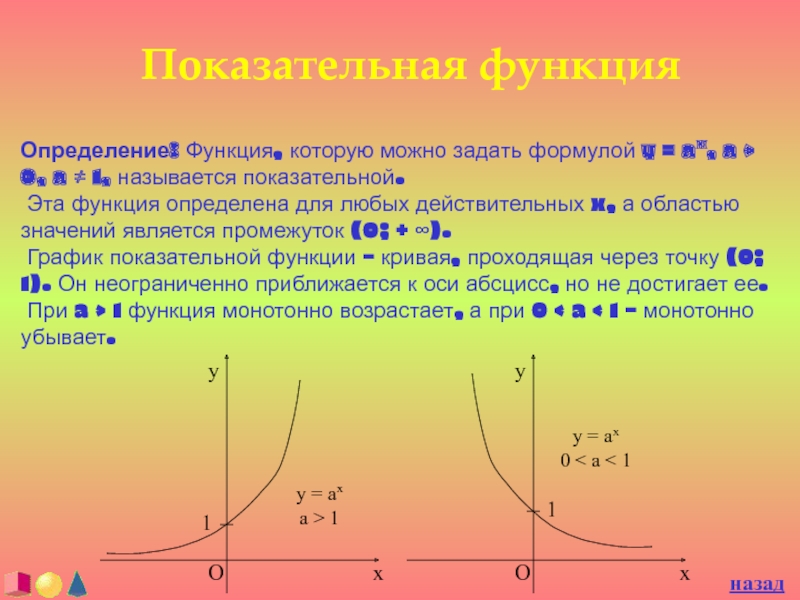
Определение: Функция, которую можно задать формулой y = ax,
a > 0, a ≠ 1, называется показательной.
Эта
функция определена для любых действительных x, а областью значений является промежуток (0; + ∞).График показательной функции – кривая, проходящая через точку (0; 1). Он неограниченно приближается к оси абсцисс, но не достигает ее.
При a > 1 функция монотонно возрастает, а при 0 < a < 1 – монотонно убывает.
назад
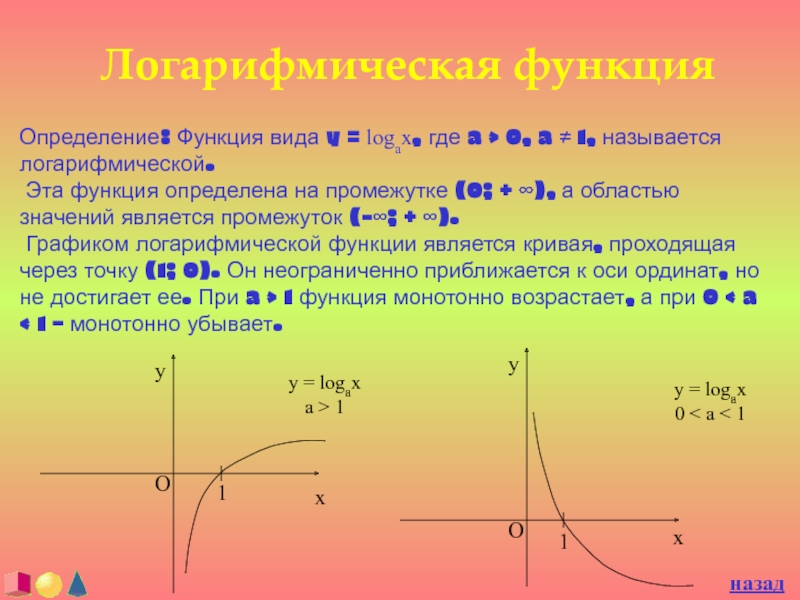
Слайд 33Логарифмическая функция
Определение: Функция вида y = logax, где a >
0, a ≠ 1, называется логарифмической.
Эта функция определена на
промежутке (0; + ∞), а областью значений является промежуток (-∞; + ∞). Графиком логарифмической функции является кривая, проходящая через точку (1; 0). Он неограниченно приближается к оси ординат, но не достигает ее. При a > 1 функция монотонно возрастает, а при 0 < a < 1 – монотонно убывает.
y = logax
a > 1
O
y
x
1
O
y
x
1
y = logax
0 < a < 1
назад
Слайд 34Тригонометрические функции
1.Функция синус.
Определение: Числовая функция, заданная
формулой y = sin x, называется синусом.
Функция определена и непрерывна на всем множестве действительных чисел. Эта функция ограничена ⏐sin x⏐≤ 1. Она периодическая, ее период T = 2πn, n ∈ Z: sin( x + 2πn) = sin x, n ∈ Z. Функция y = sin x – нечетная: sin (-x) = -sin x ее график симметричен относительно начала координат. График этой функции называется синусоидой.Функция принимает нулевые значения
При х = πn, n ∈ Z.
Функция y = sin x возрастает
на промежутках
[-π/2 + 2πn; π/2 + 2πn], n ∈ Z
и убывает на промежутках
[π/2 + 2πn; 3π/2 + 2πn], n ∈ Z
далее
назад
Слайд 35 2.Функция косинус.
Определение: Числовая функция, заданная формулой y = cos
x, называется косинусом.
Функция определена и непрерывна на
всем множестве действительных чисел. Эта функция ограничена ⏐cos x⏐≤ 1. Она периодическая, ее период T = 2πn, n ∈ Z: cos( x + 2πn) = cos x, n ∈ Z. Функция y = cos x – четная: cos (-x) = cos x ее график симметричен относительно оси ординат. График этой функции называется косинусоидой.Функция принимает нулевые значения
при х = π/2 + πn, n ∈ Z.
Функция y = cos x возрастает
на промежутках
[π + 2πn; 2π + 2πn], n ∈ Z
и убывает на промежутках
[2πn; π + 2πn], n ∈ Z
y
x
O
1
-1
−π
π
π/2
−π/2
y = cos x
5π/2
T = 2π
3π/2
2π
назад
далее
Слайд 36 3.Функция тангенс.
Определение: Числовая функция, заданная формулой y = tg
x, называется тангенсом.
Функция определена при x ≠
π/2 + πn, n ∈ Z. Ее областью значений является интервал (-∞; + ∞). Она периодическая, ее период T = πn, n ∈ Z: tg( x + πn) = tg x, n ∈ Z. Функция y = tg x – нечетная: tg (-x) = -tg x и ее график симметричен относительно начала координат. В точках x = π/2 + πn, n ∈ Z функция y = tg x не существует, и говорят, что в этих точках функция терпит разрыв, т. е. она не является непрерывной. График этой функции называется тангенсоидой.Функция принимает нулевые значения при х = πn, n ∈ Z. Функция y = tg x возрастает на всех интервалах определения (-π/2 + πn; π/2 + πn), n ∈ Z.
назад
далее
Слайд 37 4.Функция котангенс.
Определение: Числовая функция, заданная формулой y = ctg
x, называется котангенсом.
Функция определена при x ≠
πn, n ∈ Z. Ее областью значений является интервал (-∞; + ∞). Она периодическая, ее период T = πn, n ∈ Z: ctg( x + πn) = ctg x, n ∈ Z. Функция y = ctg x – нечетная: ctg (-x) = -ctg x и ее график симметричен относительно начала координат. В точках x = πn, n ∈ Z функция y = ctg x не существует, и говорят, что в этих точках функция терпит разрыв, т. е. она не является непрерывной. График этой функции называется котангенсоидой.Функция принимает нулевые значения при х = π/2 + πn, n ∈ Z. Функция y = ctg x убывает на всех интервалах определения (2πn; π + πn), n ∈ Z.
y
x
O
1
-1
π/2
−π/2
y = сtg x
π
3π/2
−π
назад











![Функции и их графики Определение 1. Пусть функция y = f(x) определена на отрезке[a; b]. Определение 1. Пусть функция y = f(x) определена на отрезке[a; b]. Говорят, что функция имеет максимум в](/img/thumbs/3cb8af3ac9490b2585678c4230969f7e-800x.jpg)
![Функции и их графики Определение 2. Пусть функция y = f(x) определена на отрезке [a; Определение 2. Пусть функция y = f(x) определена на отрезке [a; b]. Говорят, что функция имеет минимум](/img/thumbs/498f33714925bdd8ed37bac179255233-800x.jpg)