Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Квадратные уравнения
Содержание
- 1. Квадратные уравнения
- 2. Квадратное уравнение имеет действительные положительные корни, если
- 3. Квадратное уравнение имеет действительные отрицательные корни, если
- 4. Квадратное уравнение имеет действительные корни различных
- 5. Квадратное уравнение имеет действительные корни различных знаков, причем отрицательный корень имеет больший модуль, если
- 6. Расположение корней относительно заданной точки определяется направлением
- 7. ММ
- 8. ММ
- 9. ММ
- 10. Оба корня квадратного трехчлена меньше числа М,
- 11. Оба корня квадратного трехчлена больше числа
- 12. Один из корней квадратного трехчлена меньше числа
- 13. При каких значениях параметра m уравнение имеет не более одного действительного корня?
- 14. При каких значениях параметра m корни уравнения различны и положительны?
- 15. При каких значениях параметра а корни уравнения таковы, что сумма их квадратов равна 1,75?
- 16. Нахождение значений параметра, при которых решения удовлетворяют некоторому условию.
- 17. Решение уравнений для всех значений параметра а
- 18. ММ
- 19. ММ
- 20. ММ
- 21. Слайд 21
- 22. При каких значениях параметра а корни квадратного
- 23. При каких значениях параметра а оба корня
- 24. Найти все значения параметра а, при которых
- 25. Найти все значения параметра а, которых оба
- 26. Скачать презентанцию
Слайды и текст этой презентации
Слайд 4Квадратное уравнение имеет действительные корни различных знаков, причем положительный корень
имеет больший модуль, если
Слайд 5Квадратное уравнение имеет действительные корни различных знаков, причем отрицательный корень
имеет больший модуль, если
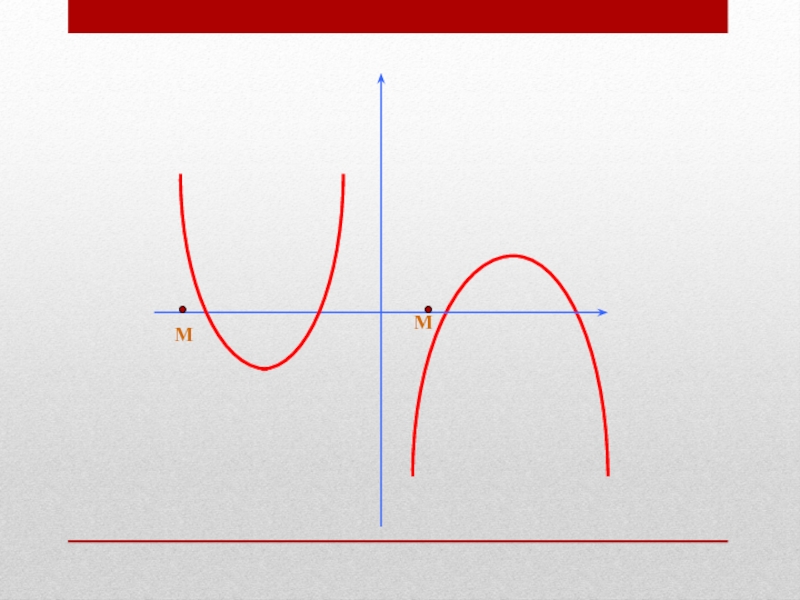
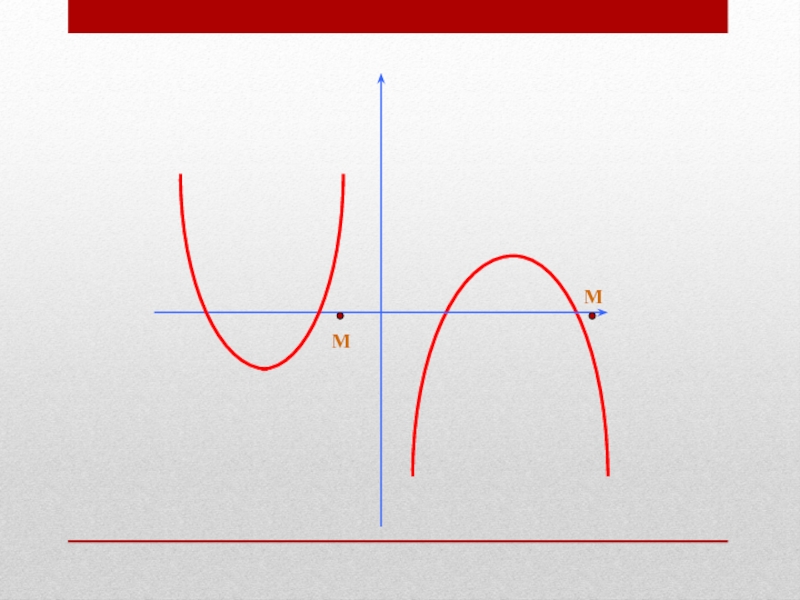
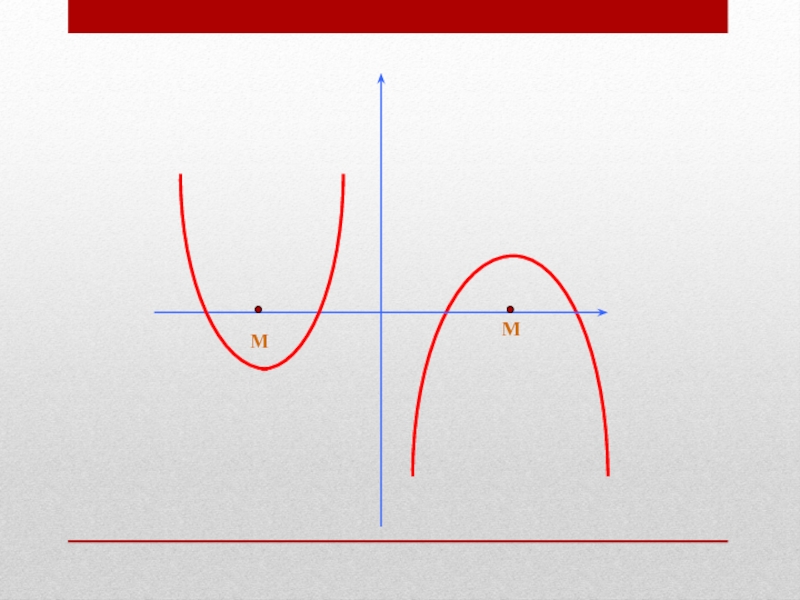
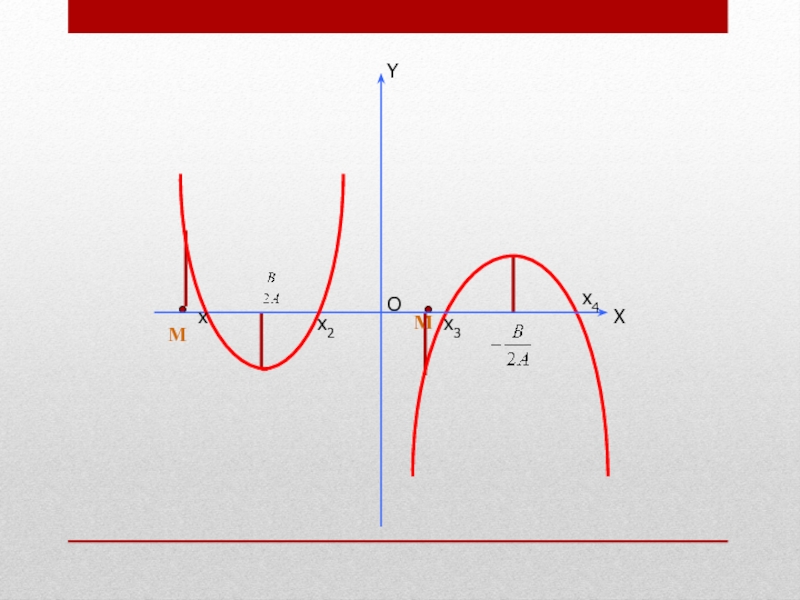
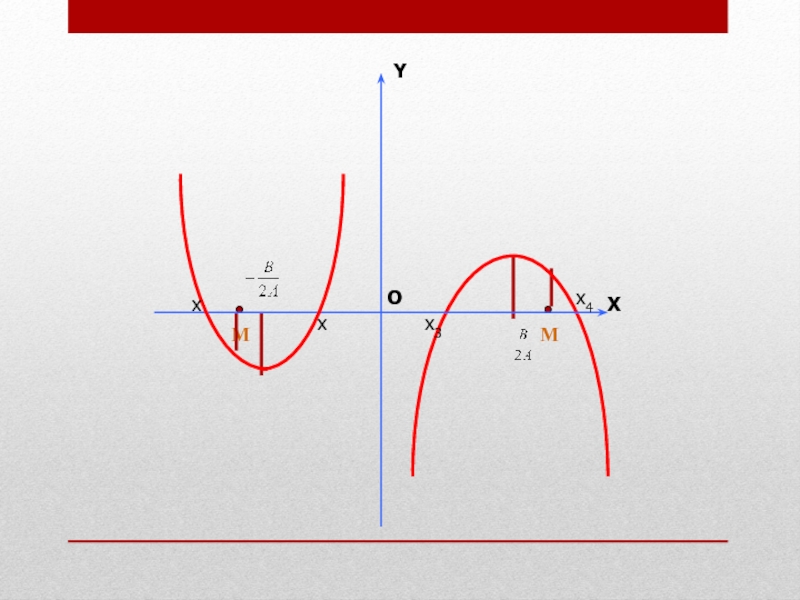
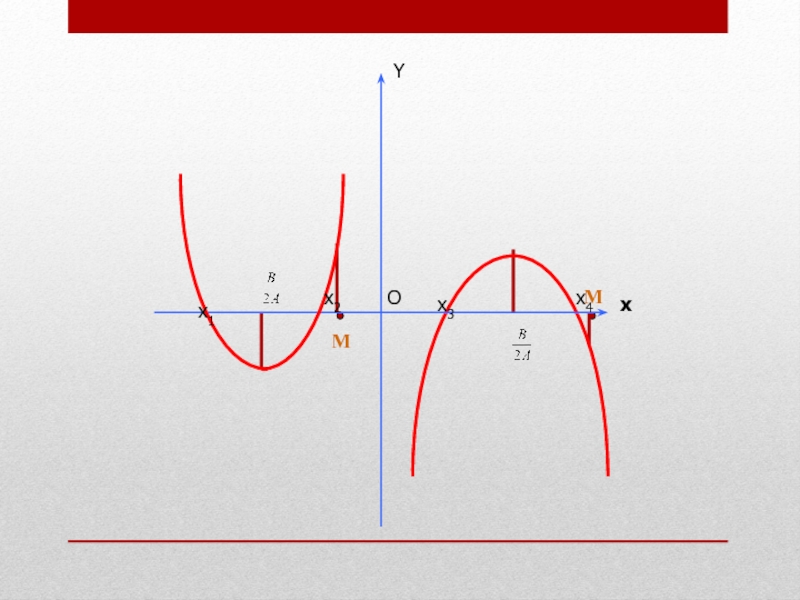
Слайд 6Расположение корней относительно
заданной точки определяется
направлением ветвей соответствующей параболы,
координатами вершины
и значениями в заданных точках.
В этих задачах
хорошо работают графические иллюстрации.
Слайд 12Один из корней квадратного трехчлена меньше числа М, а другой больше
числа М,
тогда и только тогда, когда
или
Слайд 22При каких значениях параметра а корни квадратного уравнения
х2 + (а + 1)х +
3 = 0 лежат по разные стороны от числа 2? Решение.
Рассмотрим функцию f(x)= х2 + (а + 1)х + 3.
f(2)<0;
f(2)=4+2a+2+3=2a+9<0
2a<-9
a<–4.5
Ответ. a∈(–∞;–4.5)
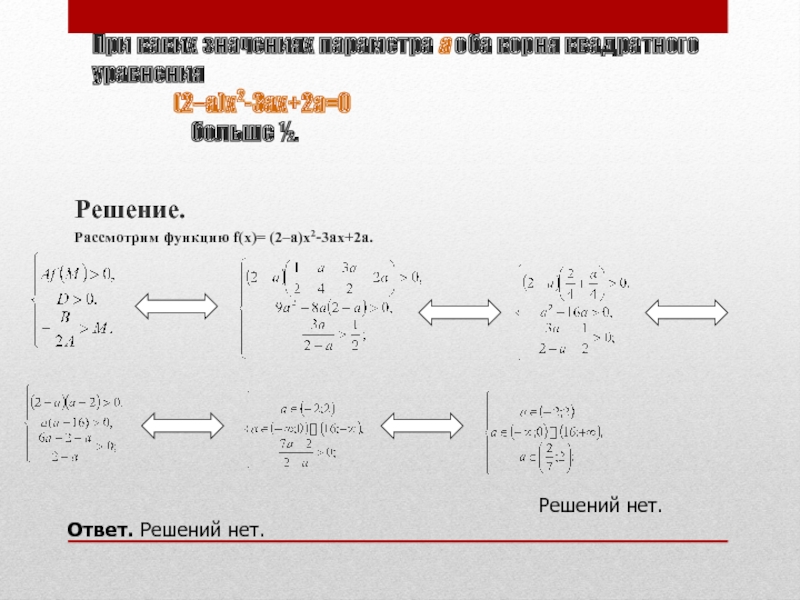
Слайд 23При каких значениях параметра а оба корня квадратного уравнения
(2–a)x2-3ax+2a=0
больше ½.Решение.
Рассмотрим функцию f(x)= (2–a)x2-3ax+2a.
Решений нет.
Ответ. Решений нет.
Слайд 24Найти все значения параметра а, при которых оба корня квадратного
уравнения
x2- 6ax+(2-2a+9a2)=0 больше 3.Решение.
Рассмотрим функцию f(x)= x2-6ax+(2-2a+9a2)
a∈
Ответ:
Слайд 25Найти все значения параметра а, которых оба корня квадратного уравнения
x2+4ax+(1-2a+4a2)=0 меньше –1.
Решение.
Рассмотрим функцию f(x)= x2+4ax+(1-2a+4a2).
Ответ. a∈
.