В чём сходство и различие тригонометрических функций?

Панюкова Марина.
Проверила учитель по математике:
Яна Валерьевна Елфимова

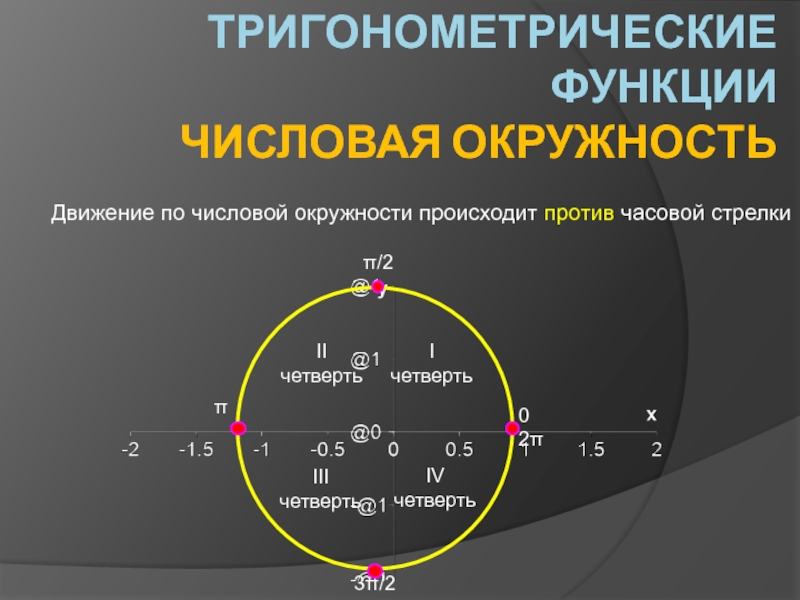
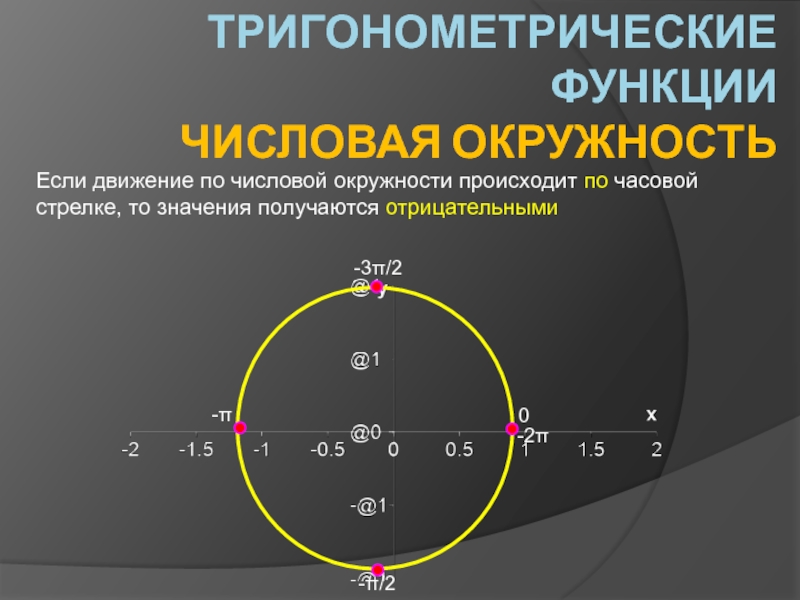
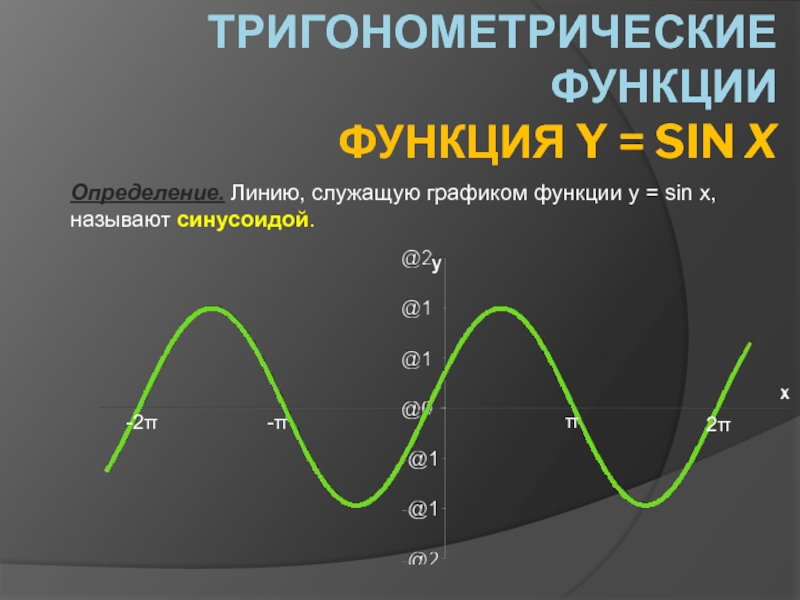
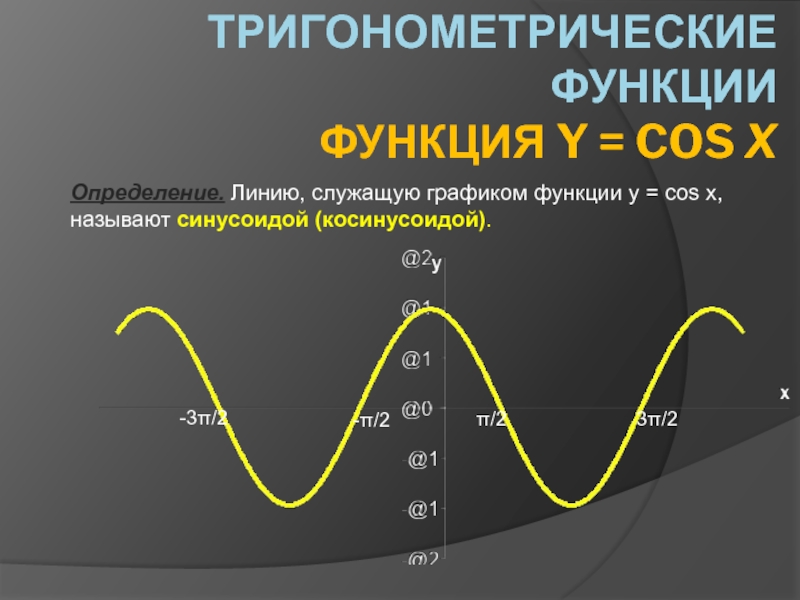
В чём сходство и различие тригонометрических функций?

Проблемный вопрос:

Учебный проект на тему: Ты, я и тригонометрия.

900igr.net

дать определения тригонометрических
функций;
- рассмотреть графики и свойства этих
функций;
- сравнить полученные

результаты;

между сторонами и углами треугольника. Тригонометрические функции угла α определяются

при помощи числовой окружности, а также из прямоугольного треугольника (для острых углов).

соответствием (между действительными числами и точками окружности).




Уравнение числовой окружности:

x2 + y2 = 1.

четверть
II четверть
III четверть
IV четверть

стрелке, то значения получаются отрицательными




0
-π/2
-π
-3π/2
-2π

то она соответствует и числу вида t + 2πk, где

параметр k – любое целое число (k є Z).

M(t)

M(t + 2πk)

соответствует числу t, то абсциссу точки М называют косинусом числа

t и обозначают cos t, а ординату точки М называют синусом числа t и обозначают sin t. 

M (t)

cos t

sin t

справедливы равенства:


Свойство 2. Для любого числа t справедливы равенства:



Свойство 3.

Для любого числа t справедливы равенства:

косинусу того же числа называют тангенсом числа t и обозначают

tg t.


Определение. Отношение косинуса числа t к синусу того же числа называют котангенсом числа t и обозначают ctg t.
 

t справедливы равенства:


Свойство 2. Для любого допустимого значения t справедливы

равенства:

функции y = sin t, y = cos t, y

= tg t, y = ctg t.

Основные соотношения, связывающие значения различных тригонометрических функций:

функции y = sin x, называют синусоидой.

2π
-π
π
-2π

SIN X.
Свойство 1. D(y) = (-∞;+∞).
Свойство 2. y = sin

x – нечетная функция.
Свойство 3. Функция y = sin x убывает на отрезке [-π/2+2πk; π/2 + 2πk] и возрастает на отрезке [π/2 + 2πk; 3π/2 + 2πk ], где k є Z.
Свойство 4. Функция ограничена и сверху и снизу (-1 ≤ sin t ≤ 1).
Свойство 5. yнаим = -1; yнаиб = 1.
Свойство 6. Функция y = sin x периодическая, ее основной период равен 2π.
Свойство 7. y = sin x – непрерывная функция.
Свойство 8. E(y) = [-1;1].
Свойство 9. Функция выпукла вверх на отрезке [0 + 2πk; π + 2πk],
выпукла вниз на отрезке [π + 2πk; 2π + 2πk], где k є Z.

функции y = cos x, называют синусоидой (косинусоидой).

-π/2
-3π/2
3π/2
π/2

COS X.
Свойство 1. D(y) = (-∞;+∞).
Свойство 2. y = cos

x – четная функция.
Свойство 3. Функция y = cos x убывает на отрезке [2πk; π + 2πk] и возрастает на отрезке [π + 2πk; 2π + 2πk ], где k є Z.
Свойство 4. Функция ограничена и сверху и снизу (-1 ≤ cos t ≤ 1).
Свойство 5. yнаим = -1; yнаиб = 1.
Свойство 6. Функция y = cos x периодическая, ее основной период равен 2π.
Свойство 7. y = cos x – непрерывная функция.
Свойство 8. E(y) = [-1; 1].
Свойство 9. Функция выпукла вверх на отрезке [-0,5π+2πk; 0,5π+2πk],
выпукла вниз на отрезке [0,5π+2πk; 1,5π+2πk], где k є Z.

Функция y = tg x возрастает на отрезке

[-π/2 + πk; π/2 + πk ], где k є Z.
Свойство 4. Функция неограничена.
Свойство 5. наибольшего и наименьшего значения функции нет.
Свойство 6. Функция y = tg x периодическая, ее период равен π.
Свойство 7. y = tg x – непрерывная функция.
Свойство 8. y = tg x – нечётная функция.
Свойство 9. Есть вертикальные асимптоты.

Свйства функции y=tg x

E(y) = (-∞;+∞).
Свойство 3. Функция y = ctg x убывает

на отрезке
[πk; π/2 + πk ], где k є Z.
Свойство 4. Функция неограничена.
Свойство 5. наибольшего и наименьшего значения функции нет.
Свойство 6. Функция y = ctg x периодическая, ее период равен π.
Свойство 7. y = ctg x – непрерывная функция.
Свойство 8. y = ctg x – нечётная функция.
Свойство 9. Есть вертикальные асимптоты.

функций» работала группа учеников 10 «Б» класса. Нам предстояло подробно

рассказать о свойствах и графиках тригонометрических функций, для того что бы узнать чем же они друг от друга отличаются. Мы постарались очень чётко изобразить графики функций, по которым видны все отличия и сходства и подобрать основные свойства. Мы считаем, что с заданием справились и эта презентация поможет нам и нашим одноклассникам разобраться в том, в чём ещё не разобрались.