Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Командировка в страну квадратных уравнений
Содержание
- 1. Командировка в страну квадратных уравнений
- 2. Задание на дом.П. 21 – 24 № 595 (а, б), 599.
- 3. Пункт №1 «Заполни пропуски» тест Пункт №2
- 4. Критерий оценивания: Нет ошибок – 5 б.1
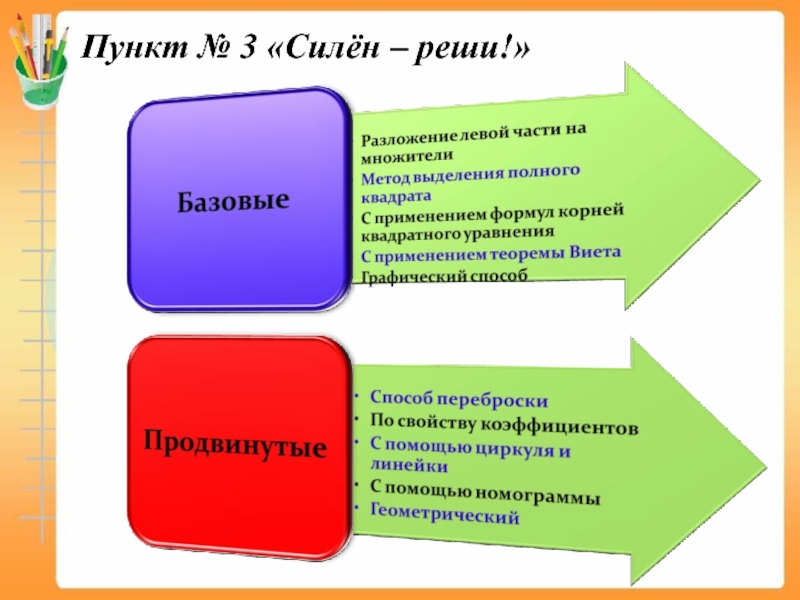
- 5. Пункт № 3 «Силён – реши!»
- 6. У = - 2х + 1у=3х2 Графический способ
- 7. Квадратные уравнения решали в Вавилоне около 2000
- 8. Немецкий математикХристиан фон Вольф(1679 – 1754 г. г.) в 1710 ввёл термин «квадратное уравнение».Полезно знать!
- 9. Способ решения квадратного уравнения, которое описал ал-ХорезмиЭтот
- 10. «Письмо из прошлого» (на папирусе)«Найти стороны поля,
- 11. Релаксация
- 12. Решение квадратных уравнений по свойству коэффициентов.Пусть дано
- 13. Хорошо…ПоработаемОтлично!
- 14. ««Человеку, изучающему алгебру, часто полезнее решить одну
- 15. Скачать презентанцию
Задание на дом.П. 21 – 24 № 595 (а, б), 599.
Слайды и текст этой презентации
Слайд 3Пункт №1 «Заполни пропуски» тест
Пункт №2 «Установи истинность» тест
Пункт №3 «Силён – реши!»
Пункт № 4 «Исторический»
Пункт №5
«Это мы не проходили…» Командировочное удостоверение
Слайд 4Критерий оценивания:
Нет ошибок – 5 б.
1 – 2 ош.
– 4б.
3 - 4 ош. - 3б.
5 - 6 ош.
– 2б.Более 6 ош. – 0 б.
Пункт №2 «Установи истинность»
Слайд 7Квадратные уравнения решали в Вавилоне около 2000 лет до нашей
эры, а Европа три года назад отпраздновала 800летие квадратных уравнений,
потому что именно в 1202 году итальянский ученый Леонард Фибоначчи изложил формулы квадратного уравнения. И лишь в 17 веке, благодаря Ньютону, Декарту и другим ученым эти формулы приняли современный вид.Пункт №4 «Исторический»
Слайд 8Немецкий математик
Христиан фон Вольф
(1679 – 1754 г. г.)
в 1710
ввёл термин «квадратное уравнение».
Полезно знать!
Слайд 9Способ решения квадратного уравнения, которое описал ал-Хорезми
Этот способ основан на
методе выделении полного квадрата.
Х2 + 10Х = 39 надо
найти число, прибавив которое к левой части, получим полный квадрат. Это число 25.
Х2 + 10Х + 25 = 39 + 25
(Х + 5)2 = 64
Х + 5 = 8
Х = 3
Ал-Хорезми работал с положительными числами, поэтому указал только один корень. Второй корень найдём из уравнения
Х + 5 = - 8
Х = - 13
Слайд 10«Письмо из прошлого» (на папирусе)
«Найти стороны поля, имеющего форму прямоугольника,
если его площадь 12, а длины равны ширине».
Слайд 12Решение квадратных уравнений по свойству коэффициентов.
Пусть дано квадратное уравнение
ах2
+ bх + с = 0, где а ≠0.
Свойство 1.
Если
а + b + с = 0 (т е. сумма коэффициентов уравнения равна нулю), то х1 = 1, х2 = с/аСвойство 2.
Если а – b + с = 0, или b = а + с, то х1 = – 1, х2 = – с/а
Пункт №6 «Это мы не проходили…».
Слайд 14««Человеку, изучающему алгебру, часто полезнее решить одну и ту же
задачу тремя различными способами, чем решить три-четыре различные задачи. Решая
одну задачу различными методами, можно путем сравнений выяснить, какой из них короче и эффективнее. Так вырабатывается опыт».У. Сойер.