Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Метод интервалов
Содержание
- 1. Метод интервалов
- 2. Повторение:Какую функцию называют непрерывной на промежутке I
- 3. Цель урока:Научиться решать неравенства методом интервалов.
- 4. Чтобы определить этот знак, достаточно вычислить значение
- 5. Пример: Решим неравенство План решения:Рассмотрим функцию
- 6. Определим знаки функции в каждом интервале:Неравенство нестрогое,
- 7. Решите неравенства:№ 244 (а, г)№ 245 (а,
- 8. Выполни задания:Сформулируй свойство непрерывных функций.Повтори план решения неравенств методом интервалов.
- 9. Домашнее задание:П. 18, № 244 (б);
- 10. Спасибо за работу!
- 11. Скачать презентанцию
Повторение:Какую функцию называют непрерывной на промежутке I ?Если функция непрерывна в каждой точке этого промежутка.Сформулируйте свойство непрерывных функций.Если на интервале (а;в) функция f непрерывна и не обращается в нуль, то она
Слайды и текст этой презентации
Слайд 2Повторение:
Какую функцию называют непрерывной на промежутке I ?
Если функция непрерывна
в каждой точке этого промежутка.
Сформулируйте свойство непрерывных функций.
Если на интервале
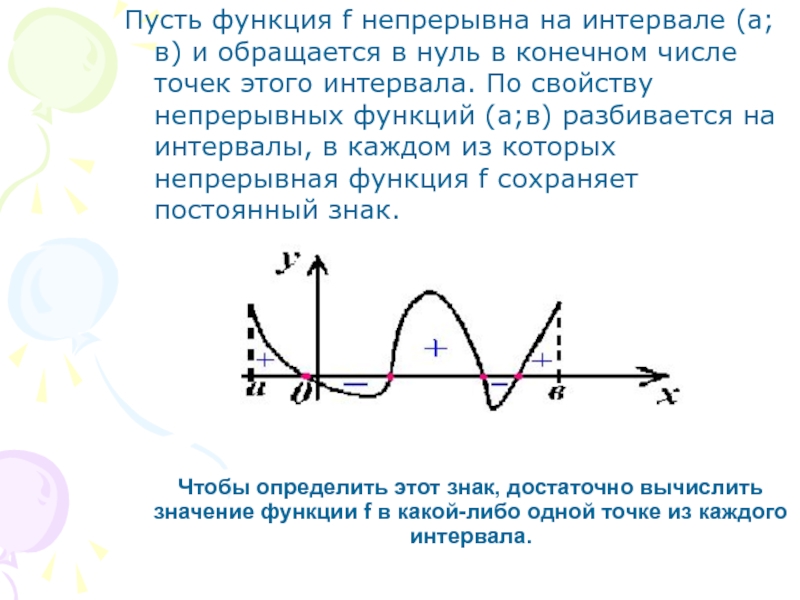
(а;в) функция f непрерывна и не обращается в нуль, то она на этом интервале сохраняет постоянный знак.Слайд 4Чтобы определить этот знак, достаточно вычислить значение функции f в
какой-либо одной точке из каждого интервала.
Пусть функция f непрерывна на
интервале (а;в) и обращается в нуль в конечном числе точек этого интервала. По свойству непрерывных функций (а;в) разбивается на интервалы, в каждом из которых непрерывная функция f сохраняет постоянный знак.Слайд 5Пример: Решим неравенство
План решения:
Рассмотрим функцию F(x)=
Найдем область определения
функции:
Вся числовая прямая, кроме нулей знаменателя:
D=R без точек2;3.Найдём нули функции:
Отметим на числовой прямой найденные точки:
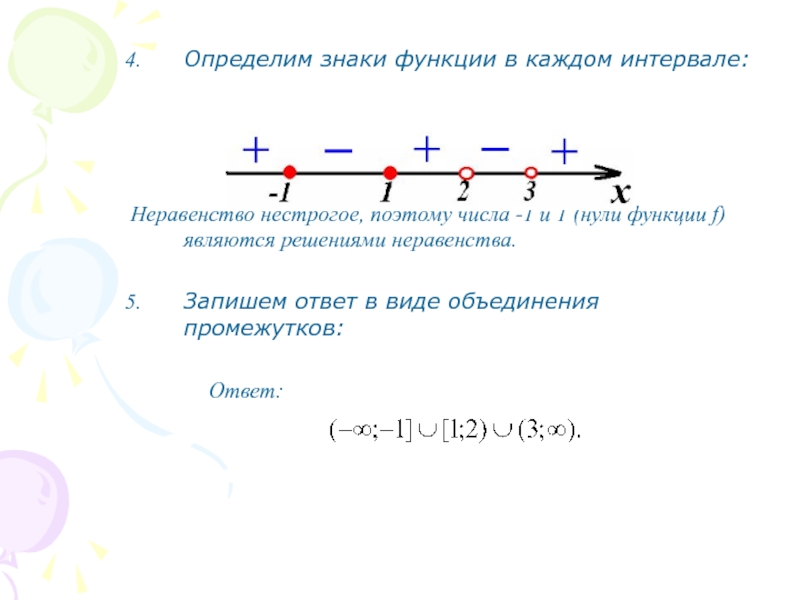
Слайд 6Определим знаки функции в каждом интервале:
Неравенство нестрогое, поэтому числа -1
и 1 (нули функции f) являются решениями неравенства.
Запишем ответ в
виде объединения промежутков:Ответ:
Слайд 7Решите неравенства:
№ 244 (а, г)
№ 245 (а, б)
№246 (в)
№ 248
(б)
№ 249 (б)
Дополнительно: с 126 пример 2, № 243 (в)
Слайд 8 Выполни задания:
Сформулируй свойство непрерывных функций.
Повтори план
решения неравенств методом интервалов.
Слайд 9Домашнее задание:
П. 18, № 244 (б);
№ 245 (г);
№ 246 (б);№ 248 (а);
№ 249 (в);
№ 243 (б,в).
Подготовиться к самостоятельной работе