Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основные понятия алгебры логики
Содержание
- 1. Основные понятия алгебры логики
- 2. Логические основы работы компьютера
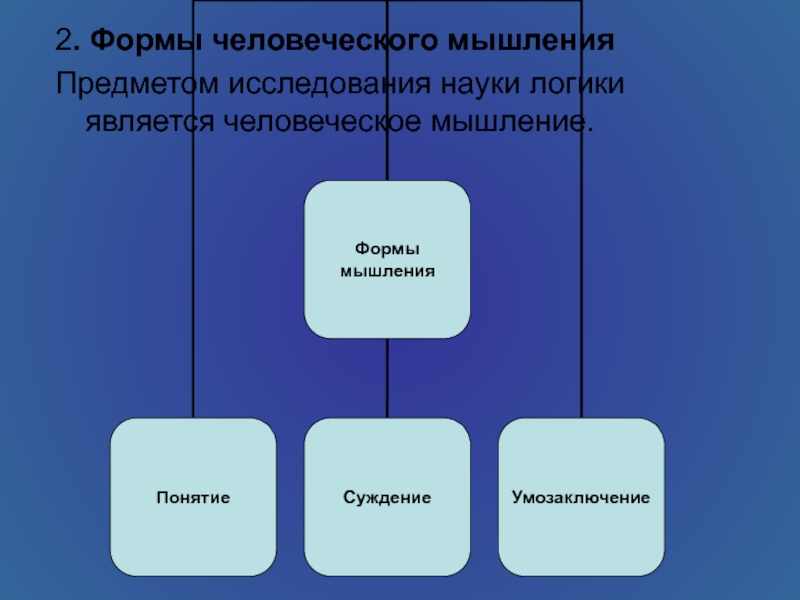
- 3. 2. Формы человеческого мышленияПредметом исследования науки логики является человеческое мышление.
- 4. Понятие – форма мышления, в которой отражаются
- 5. Основные логические характеристики понятия: содержание и объём.Содержание
- 6. Наглядная геометрическая иллюстрация объёмов понятий и отношений
- 7. Суждение (высказывание, утверждение) – форма мышления, в
- 8. Основной принцип формальной логики: правильность рассуждения (умозаключения)
- 9. 2. Логика – наука, изучающая законы и
- 10. 3. Отношения между понятиямиПо отношению друг к
- 11. Обозначения сравнимых совместимых понятийX, YX YX YТождествоПересечениеПодчинениеX
- 12. Обозначения сравнимых несовместимых понятийАА ВСоподчинениеПротивоположностьПротиворечиеА – березаВ
- 13. Понятие об алгебре высказываний
- 14. Алгебра логики – это математический аппарат, с
- 15. Высказывание может принимать только оно из двух
- 16. Простое высказывание (логическая переменная) содержит только одну
- 17. Значение логической функции можно определить с помощью
- 18. Логические операции и схемы
- 19. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Основные понятия алгебры логики
Законы правильного мышления
Познание истины – одна из
важнейших потребностей человека.
Слайд 32. Формы человеческого мышления
Предметом исследования науки логики является человеческое мышление.
Слайд 4Понятие – форма мышления, в которой отражаются отличительные существенные признаки
предметов.
Примеры понятий: апельсин, трапеция, белизна, река Нил, ураганный ветер, студент
медицинского института.Существенными называются такие признаки, каждый из которых, взятый отдельно, необходим, а все вместе достаточны, чтобы с их помощью отличить (выделить) данный предмет (явление) от всех остальных и сделать обобщение, объединив однородные предметы в множество.
Пример: апельсин – круглый, оранжевый, упругий, сладкий, ароматный.
Слайд 5Основные логические характеристики понятия: содержание и объём.
Содержание понятия – совокупность
существенных признаков, отражённых в этом понятии.
Пример: ромб –параллелограмм, у которого
все стороны равны.Объём понятия – множество предметов, каждому из которых принадлежат признаки, составляющие содержание понятия.
Пример: объём понятия ученик – люди, которые когда-либо учились, учатся сейчас или будут учиться когда-нибудь.
Слайд 6Наглядная геометрическая иллюстрация объёмов понятий и отношений между ними была
предложена математиком, физиком и астрономом
Леонардом Эйлером (1707 – 1781)
и носит название кругов Эйлера.
Слайд 7Суждение (высказывание, утверждение) – форма мышления, в которой что-либо утверждается
или отрицается о предмета, их свойствах или отношениях между ними.
Примеры:
Этот апельсин вкусный. Если пошёл дождь, то на улице весна.Суждения бывают простыми и сложными.
Наступила весна – простое суждение.
Наступила весна, и прилетели грачи – сложное суждение.
Всякое суждение может быть истинным или ложным.
Содержание суждения – это то, о чём в нем идёт речь, его смысл.
Логическая форма суждения – это его строение, способ связи его составных частей.
Умозаключение – форма мышления, посредством которой из одного или нескольких суждений, называемых посылками, мы по определённым правилам вывода получаем суждение-заключение (вывод умозаключения).
Все люди смертны.
Сократ – человек.
Сократ смертен.
Слайд 8Основной принцип формальной логики: правильность рассуждения (умозаключения) определяется только его
логической формой (структурой) и не зависит от конкретного содержания входящих
в него суждений.С точки зрения содержания, суждения, входящие в рассуждения могут быть истинными или ложными ( истинно или ложно отражать действительность), а если рассматривать рассуждение со стороны формы, то имеет значение только его логическая правильность ли неправильность.
Слайд 92. Логика – наука, изучающая законы и формы мышления.
Этапы развития
логики
I этап – формальная логика. Основатель – Аристотель (384 –
322 гг. до н.э.), ввел основные формы абстрактного мышления.II этап – математическая логика. Основатель – немецкий ученый и философ Лейбниц (1642 – 1716), предпринял попытку логических вычислений.
III этап – математическая логика (булева алгебра). Основатель – английский математик Джордж Буль (1815 – 1864), ввёл алфавит, орфографию и грамматику для математической логики.
Слайд 103. Отношения между понятиями
По отношению друг к другу понятия делятся
на сравнимые и несравнимые.
Далёкие друг от друга по своему содержанию
понятия, не имеющие общих признаков, называются несравнимыми.Несравнимые понятия: Романс и кирпич.
Сравнимые понятия делятся по объёму на совместимые (объёмы этих понятий совпадают полностью или частично) и несовместимые (объёмы которых не совпадают ни по одному элементу).
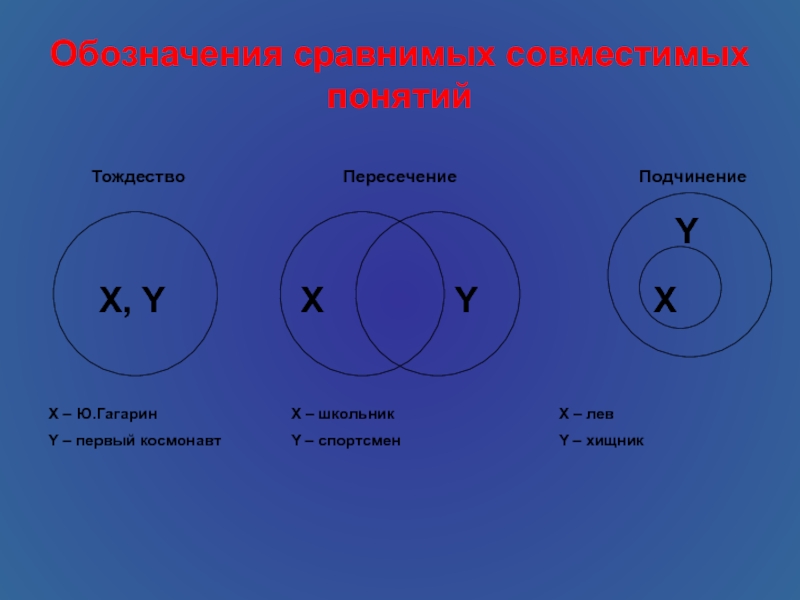
Слайд 11Обозначения сравнимых совместимых понятий
X, Y
X
Y
X
Y
Тождество
Пересечение
Подчинение
X – Ю.Гагарин
Y –
первый космонавт
X – школьник
Y – спортсмен
X – лев
Y – хищник
Слайд 12Обозначения сравнимых несовместимых понятий
А
А
В
Соподчинение
Противоположность
Противоречие
А – береза
В – ель
С -
дерево
А – большой дом
В – маленький дом
А – большой дом
В
–небольшой домА
В
С
В
Слайд 14Алгебра логики – это математический аппарат, с помощью которого записывают
(кодируют), упрощают, вычисляют и преобразуют логические высказывания.
По высказыванием (суждением) будем
понимать повествовательное предложение относительно которого можно сказать истинно оно или ложно.Слайд 15Высказывание может принимать только оно из двух логических значений –
истинно (1) или ложно (0).
Обозначать высказывания будем прописными буквами.
А =
{Солнце светит для всех} = 1 В = {Все ученики любят информатику} = 0
С = {Некоторые из учеников любят информатику} = 1
D= {А ты любишь информатику?}
Е = {Посмотри в окно}
Ж = {2*x – 5 >0} – не высказывание
З = {x*x <0} = 0
Слайд 16
Простое высказывание (логическая переменная) содержит только одну простую мысль.
А
= {Квадрат – это ромб}
Сложное высказывание (логическая функция) содержит несколько
простых мыслей, соединённых между собой с помощью логических операций.F(А,В) = {Лил дождь, и дул холодный ветер}
А
В