Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Показательная функция. Решение показательных уравнений 11 класс
Содержание
- 1. Показательная функция. Решение показательных уравнений 11 класс
- 2. Функцию вида называют показательной функцией
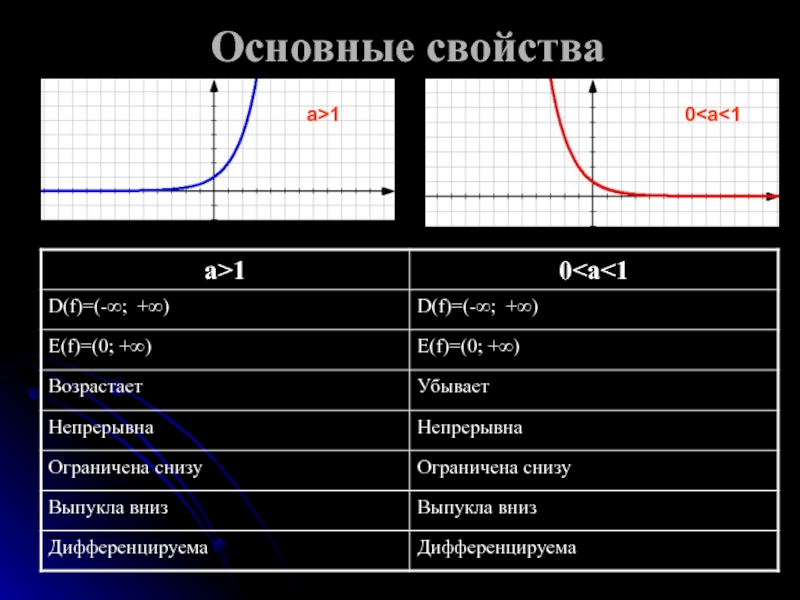
- 3. Основные свойства а>1 0
- 4. Какие из перечисленных ниже функций являются
- 5. Какие из перечисленных показательных функций являются возрастающими:1)y
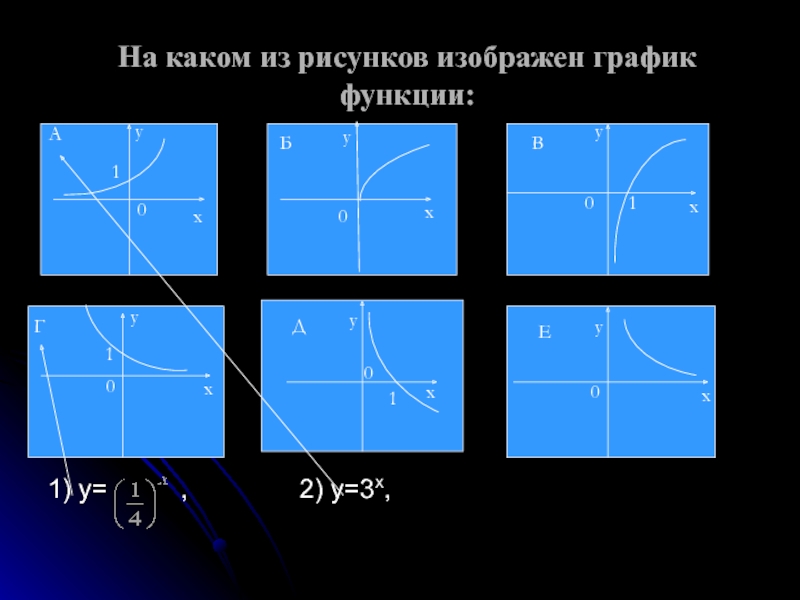
- 6. На каком из рисунков изображен график функции:1)
- 7. На рисунке изображены графики показательных функций. Соотнесите график функции с формулой.1)2)3)4)
- 8. Назовите функцию, возрастающую (убывающую) на множестве действительных чисел. Соотнесите график с соответствующей формулой.а)б)
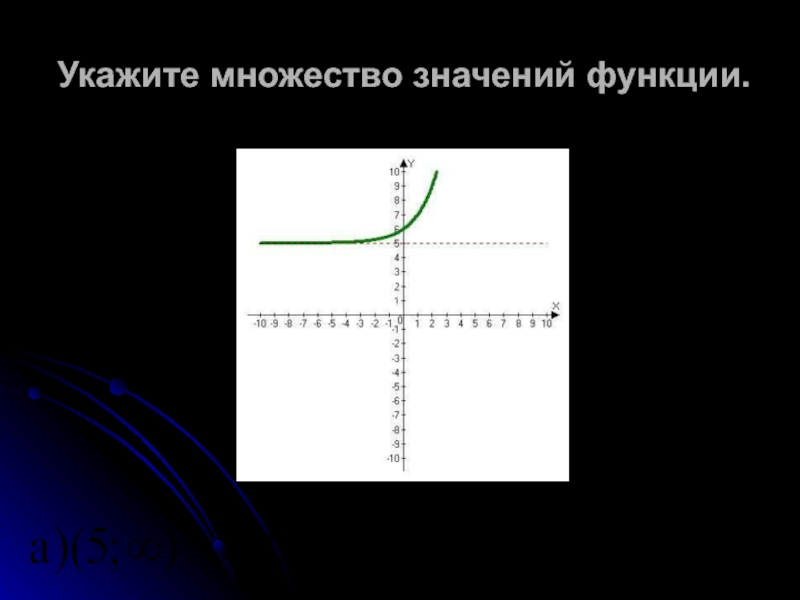
- 9. Укажите множество значений функции.а) (5;
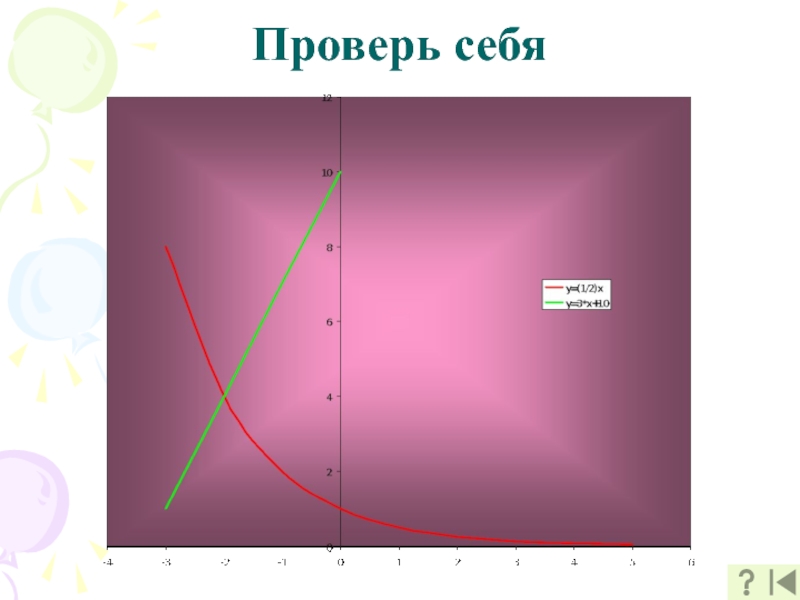
- 10. Проверь себя
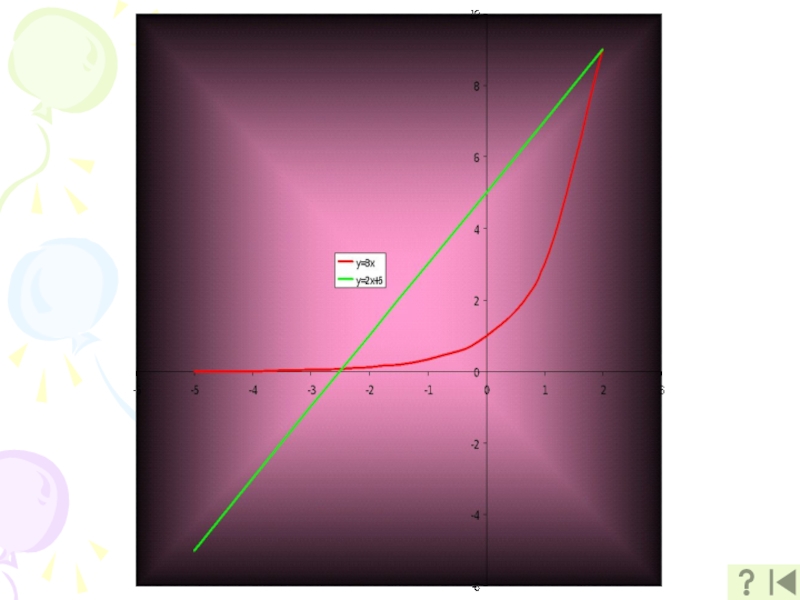
- 11. Слайд 11
- 12. Проверим правильность построения графиков01ху-1у = 0,5х-10ху14у = 3х-4
- 13. Показательные уравненияУравнения вида a f (x)
- 14. 1. Простейшие показательные уравнения
- 15. Решите уравнения ( устно):5 х =25х=27 х-2
- 16. 2. Метод приведения к одному основанию
- 17. 2. Метод приведения к одному основанию
- 18. Уравнения приводимые к квадратным9 – 26⋅3 –
- 19. 4sinx+21+sinx-8=022sinx+2∙2sinx-8=0, 2sinx =t, t>0. t²+2t-8=0, t1=-4, t2=2.t1=-4
- 20. 3. Способ подстановки
- 21. 4. Метод почленного деления
- 22. 5. Способ группировки
- 23. (3х²-81)∙√1-х=0Решение:Произведение двух выражений равно нулю, если хотя
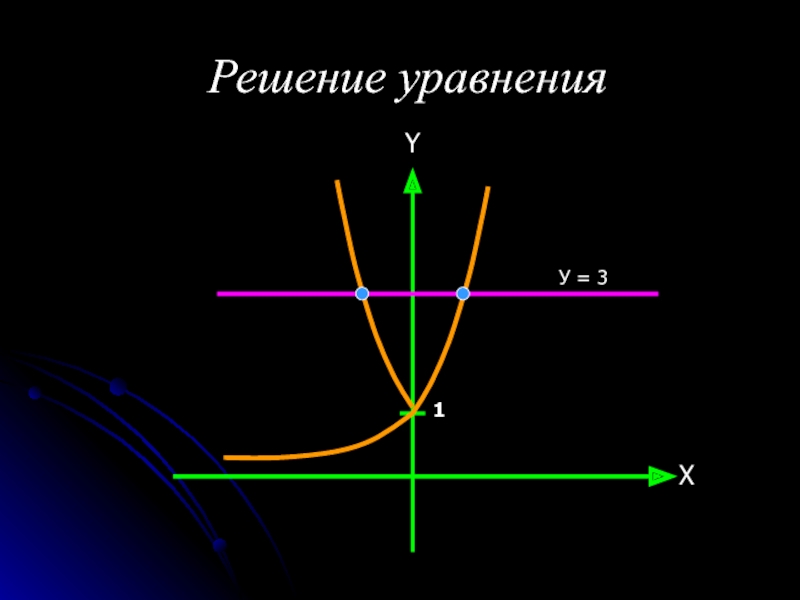
- 24. Решение уравнения У = 3XY1
- 25. Методы решения показательных уравнений 1. Простейшие показательные
- 26. Цели урока: углубление понимания сущности различных методов
- 27. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Показательная функция.
«Решение показательных уравнений»
ЦОР к уроку подготовлен учителем математики
Слайд 4 Какие из перечисленных ниже функций являются показательными
1) y =
2x;
2) y = x2 ;
3) y =(-3)x;
4)
y =(√2 )x; 5) y = x;
6) y =(x - 2)3;
7) y = π x;
8) y = 3-x.
Слайд 5Какие из перечисленных показательных функций являются возрастающими:
1)y = 5x;
2)
y = (0,5)x;
3) y =(√ 2 )x;
4)
y = 10x; 5) y = π x;
6) y= (⅔)x;
7) y =(14 cos(π /3))-x.
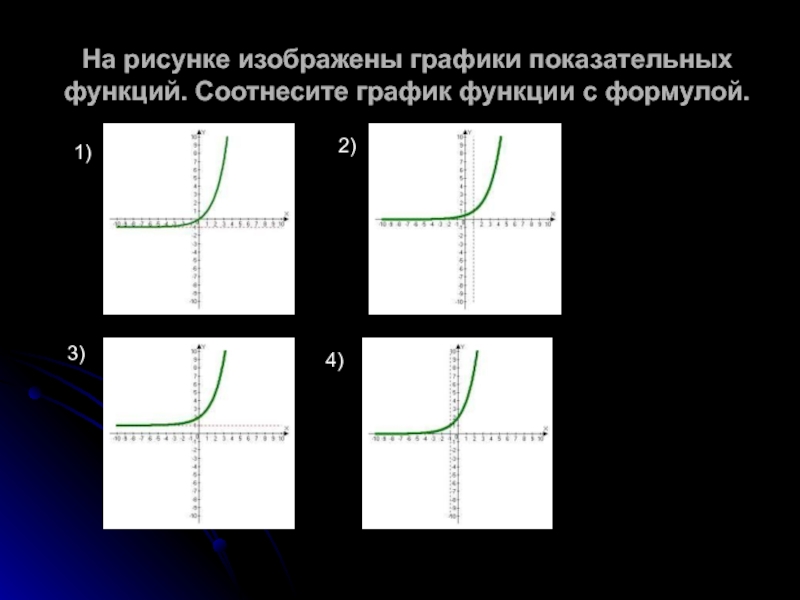
Слайд 7На рисунке изображены графики показательных функций. Соотнесите график функции с
формулой.
1)
2)
3)
4)
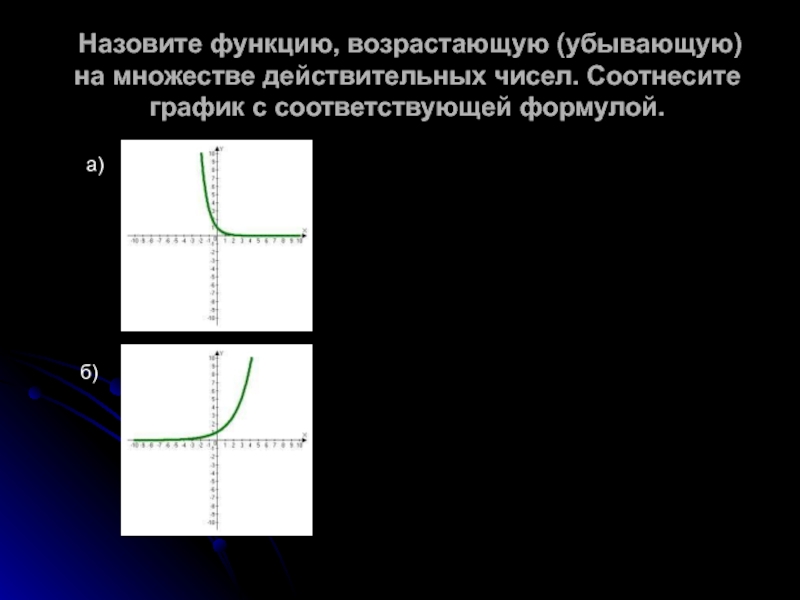
Слайд 8 Назовите функцию, возрастающую (убывающую) на множестве действительных чисел. Соотнесите
график с соответствующей формулой.
а)
б)
Слайд 13Показательные уравнения
Уравнения вида a f (x) = a g
(x) (где а >0,
а ≠ 1) и уравнения,
сводящиеся к этому виду называются показательными.Простейшие показательные уравнения:
a a a = a = a = b a = b ( a = b (a a = b (a a = b (a = a = b (a = 1).
Уравнения вида
aa a =a = a = aa = a .
Функционально – графический
Уравнения приводимые к квадратным.
Способы решения показательных уравнений
ff f (x)
ff f (x)
ff f (x)
g(x)
Слайд 15Решите уравнения ( устно):
5 х =25
х=2
7 х-2 =49
х=4
4 х =1
х
= 0
5,7 х-3 = 1
х = 3
2 2 х =64
х
= 53 9 х =81
х = 1,5
5 х =7 х
х = 0
3,4 х+2 =4,3 х+2
х = -2
Слайд 162. Метод приведения к одному основанию
20,5x = 30,5x
30,5x >
0
(2/3) 0,5x = 1
0,5х = 0
х = 0
Ответ:
0 4х+1 + 4х = 320
4х . 4 + 4х = 320
4х(4 + 1) = 320
4х = 64
4х = 43
х = 3
Ответ: 3.
a f (x) = a g (x)
Слайд 18Уравнения приводимые к квадратным
9 – 26⋅3 – 27 = 0,
(3х)
– 26 3 – 27 = 0,
Пусть 3 = t,
t> 0, тогда:t – 26 t– 27 = 0,
а + с = b
t1 = - 1 не имеет смысла, т.к. t> 0.
t2= 27 Переходим к переменной х:
3 = 27,
3 = 3 ,
х = 3.
Ответ: 3
х
х
х
2
х
2
х
х
3
Слайд 194sinx+21+sinx-8=0
22sinx+2∙2sinx-8=0, 2sinx =t, t>0.
t²+2t-8=0, t1=-4, t2=2.
t1=-4 не удовлетворяет условию
t>0.
Вернемся к переменной х, получаем 2sinx =2, sinx=1, х=
.Ответ: .
Слайд 23(3х²-81)∙√1-х=0
Решение:
Произведение двух выражений равно нулю, если хотя бы один из
множителей равен нулю, а другой при этом не теряет смысла.
3х²-81=0,
3х²=34, х²=4, х=2 или х=-2.При х=2 подкоренное выражение отрицательно, значит, число 2 не является корнем исходного уравнения.√1-х=0 при х=1.Это число является корнем исходного уравнения, так как выражение 3х²-81имеет смысл при любом х.
Ответ: -2; 1.
Слайд 25Методы решения
показательных уравнений
1. Простейшие показательные уравнения.
2. Метод приведения к одному
основанию.
3. Способ подстановки.
4. Метод почленного деления.
5. Способ группировки.
Слайд 26Цели урока:
углубление понимания сущности различных методов решения показательных уравнений
для получения новых знаний;
установление внутрипредметных связей;
воспитание у учащихся
культуры мышления; формирование умений осуществлять самоконтроль и взаимоконтроль
формирование умений анализировать, устанавливать связи и отношения;
формирование умений строить логическую цепочку рассуждений;
формирование умений проводить обобщение, переносить знания в новую ситуацию;
формирование навыков коллективной и индивидуальной работы;