лишь поясняется при помощи примеров: множество книг на полке, множество
точек на прямой (точечное множество) и т. д.Множества принято обозначать прописными буквами латинского алфавита: A, B, C… Z.
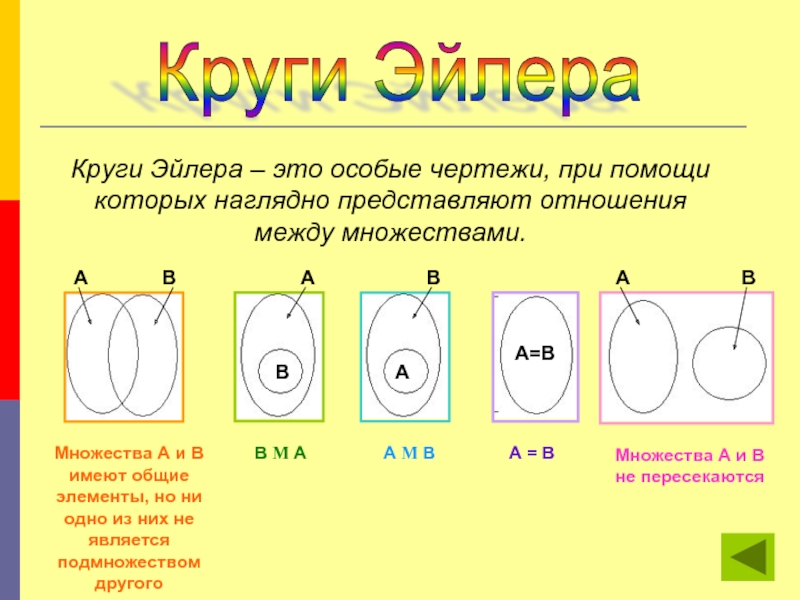
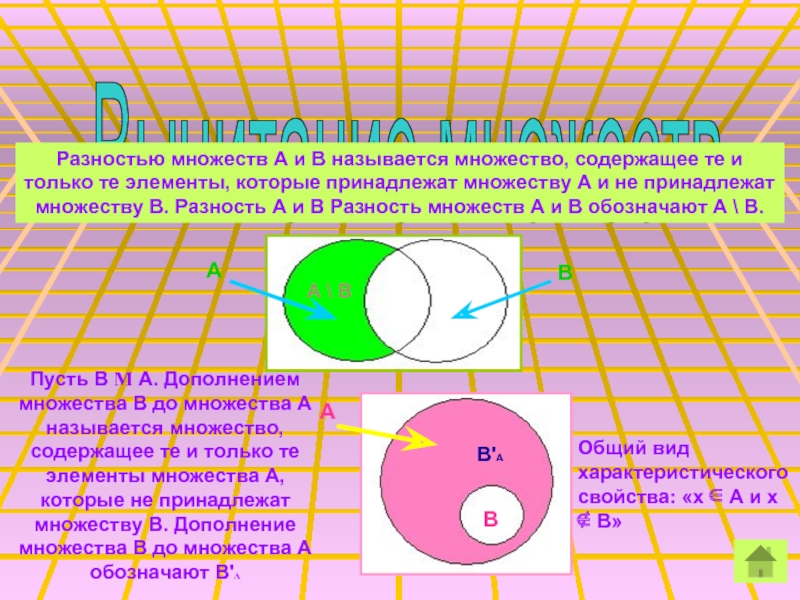
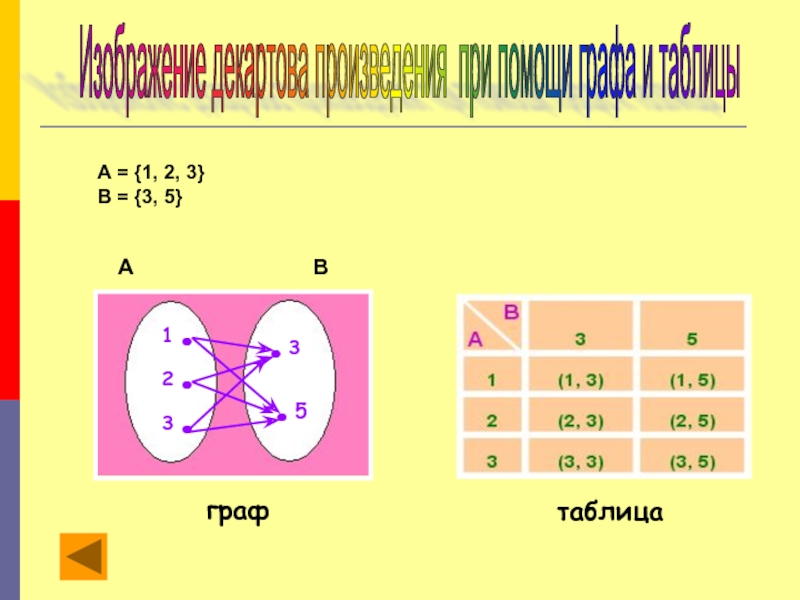
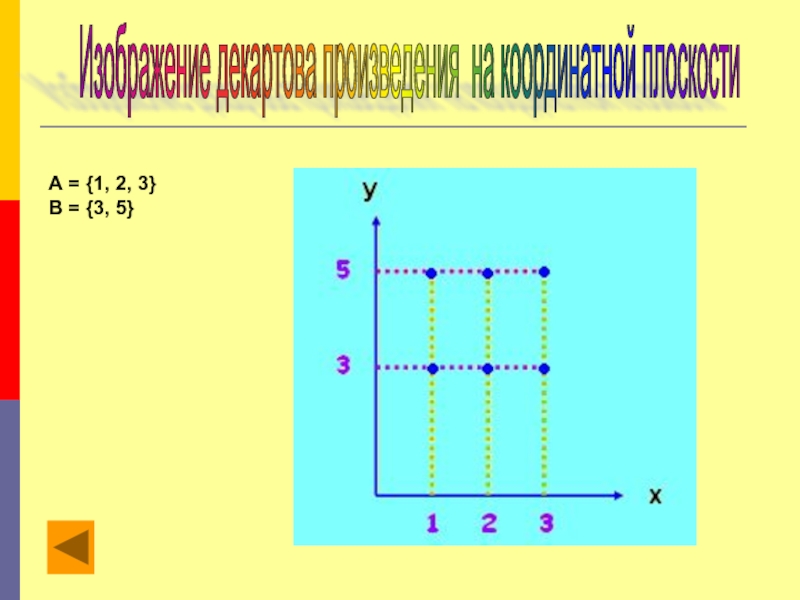
МНОЖЕСТВО
Множество дней недели,
Множество месяцев в году
Множество точек на прямой,
Множество натуральных чисел