Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Прогрессия
Содержание
- 1. Прогрессия
- 2. Цели урока: Проверить, оценить глубину знаний
- 3. Оборудование Листы для индивидуальной работы Таблица «Прогрессия» Справочный индивидуальные таблицы «Степени чисел 2 и3»
- 4. Постановка задачи перед учащимися Проанализировать свой уровень
- 5. Проверка знания определений и формул прогрессий Индивидуальная
- 6. Самоконтроль выполнения задания по таблице «Прогрессия» Учащиеся
- 7. Актуализация опорных знаний Устная работа (фронтально)по вопросам
- 8. Контроль умений и знаний Проверка умений
- 9. Контроль умений и знаний А. Индивидуальная работа
- 10. Контроль умений и знаний А. Индивидуальная работа
- 11. Самоконтроль выполнения задания по заполненной таблице Учащиеся
- 12. Коррекция знаний Б. Устная работа (фронтально): Как
- 13. Контроль умений и знаний Проверка умений по
- 14. 3 задача. Срочный вклад, положенный в
- 15. 7 задача. Докажите, что если последовательность
- 16. Задание на дом Дифференцированно задание по карточкам
- 17. Скачать презентанцию
Цели урока: Проверить, оценить глубину знаний и умений учащихся по теме «Прогрессия» Проверить готовность учащихся к контрольной работе Сформировать стремление к умственному совершенствованию, самоанализу своей деятельности
Слайды и текст этой презентации
Слайд 2Цели урока:
Проверить, оценить глубину знаний и умений учащихся по
теме «Прогрессия»
Проверить готовность учащихся к контрольной работе
Сформировать стремление
к умственному совершенствованию, самоанализу своей деятельностиСлайд 3Оборудование
Листы для индивидуальной работы
Таблица «Прогрессия»
Справочный индивидуальные таблицы
«Степени чисел 2 и3»
Слайд 4Постановка задачи перед учащимися
Проанализировать свой уровень готовности
к контрольной
работе в процессе выполнения
заданий
Примечание: на рабочем столе каждого школьника
только:1. Справочный материал «Таблицы степени чисел 2 и 3»;
2. Индивидуальные листы с заданиями;
3. Чистые листки бумаги для выполнения работы.
Слайд 5Проверка знания определений и формул прогрессий
Индивидуальная работа с 1
листом заданий
а) Записать формулы, которые задают
арифметическую прогрессию;
геометрическую прогрессиюб) Записать формулы для разности арифметической прогрессии и знаменателя геометрической прогрессии
в) Заполнить таблицу
Слайд 6Самоконтроль выполнения задания
по таблице «Прогрессия»
Учащиеся проверяют правильность записей по
таблице,
которую открывает учитель
Учащиеся красной пастой отмечают допущенные ошибки
Слайд 7Актуализация опорных знаний
Устная работа (фронтально)по вопросам учителя:
Сформулировать определение арифметической
прогрессии,
геометрической прогрессии
Найти сходство и различие в
определениях (если они имеются)Привести примеры конечной и бесконечной арифметической прогрессии, конечной и бесконечной геометрической прогрессии
Перечислить способы задания последовательности (привести примеры)
Что выражает формула n- ого члена последовательности?
Что выражает рекуррентная формула?
Слайд 8Контроль умений и знаний
Проверка умений по выполнению заданий
репродуктивного характера (применение формул n –ого члена прогрессии и суммы
n первых членов прогрессии)А. Индивидуальная работа со 2 листом заданий (3 уровня сложности)
Примечание: двое у доски – 2 и 3 уровни, остальные работает на местах
1 уровень. Заполнить таблицы:
№1.
№2.
Слайд 9Контроль умений и знаний
А. Индивидуальная работа со 2
листом заданий
2 уровень. Заполнить таблицы:
№1.
№2.
Слайд 10Контроль умений и знаний
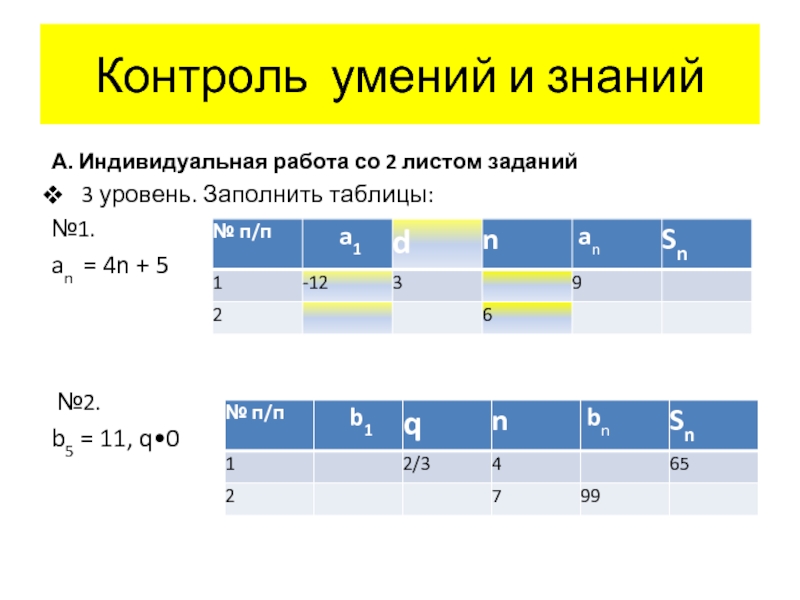
А. Индивидуальная работа со 2 листом
заданий
3 уровень. Заполнить таблицы:
№1.
an
= 4n + 5№2.
b5 = 11, q•0
Слайд 11Самоконтроль выполнения задания по заполненной таблице
Учащиеся проверяют правильность
записей по таблице,
которую открывает учитель
Учащиеся красной пастой отмечают
допущенные ошибкиСлайд 12Коррекция знаний
Б. Устная работа (фронтально):
Как выразить из формулы
n- ого члена арифметической прогрессии a1 и d
?Как выразить из формулы n- ого члена геометрической прогрессии b1 и q?
В геометрической прогрессии выразить:
а) a10 через a2, a4, a5, a7
б) a4 через a6, a8, a11 .
Слайд 13Контроль умений и знаний
Проверка умений по применению знаний
Письменная
работа в группах «Ты мне, я тебе»
Примечание: каждые два человека
из группы решают только одну задачу;учитель предлагает для работы 8 задач двух уровней сложности;
учащиеся дают друг другу задания из предложенных задач;
учитель оценивает работы после урока.
1 задача. Тело в первую секунду прямолинейного движения прошло 16м,
а в каждую следующую секунду проходило на 3м больше, чем в
предыдущую. Какой путь прошло это тело за 7 секунд?
2 задача. Представить в виде обыкновенной дроби периодическую
десятичную дробь 0, 6(7)
Слайд 14 3 задача. Срочный вклад, положенный в сберегательный банк,
четыре года, если в начале он был равен 10000 рублей?
4 задача. В равносторонний треугольник со стороной 6 см вписан
треугольник, вершинами которого служат середины сторон
данного треугольника. В полученный треугольник таким же
способом вписан новый и т.д. Найдите сумму периметров
этих треугольников.
5 задача. Определите первый член и знаменатель геометрической
прогрессии, если известно, что разность между её пятым и
третьим членами равна 72, а разность между четвертым и
вторым членами равна 36.
6 задача. Решите уравнение, в котором слагаемые в сумме ,
записанные в левой части, составляют арифметическую
прогрессию: 2+ 6 + 10 + … + х = 450.
Слайд 15 7 задача. Докажите, что если последовательность (an)
арифметическая
прогрессия, то a2 + an-2 = a5 + an-58 задача. Геометрическая прогрессия состоит из 15 членов. Сумма
первых пяти членов равна 11/64 , а сумма следующих пяти
членов равна – 11/2. Найти сумму последних пяти членов
этой прогрессии.
Слайд 16Задание на дом
Дифференцированно задание по карточкам
Примечание: каждый ученик
выбирает себе задание из
предложенных учителем задач(3 уровня сложности)
Теги