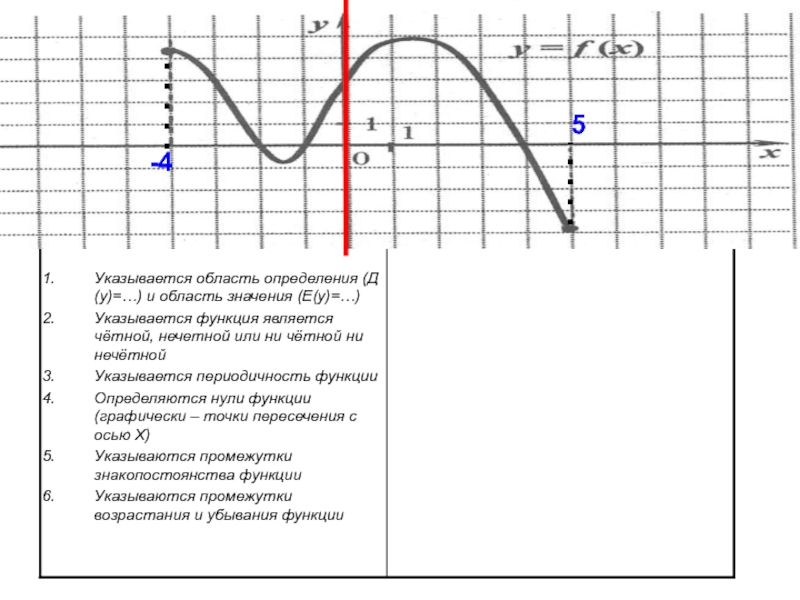
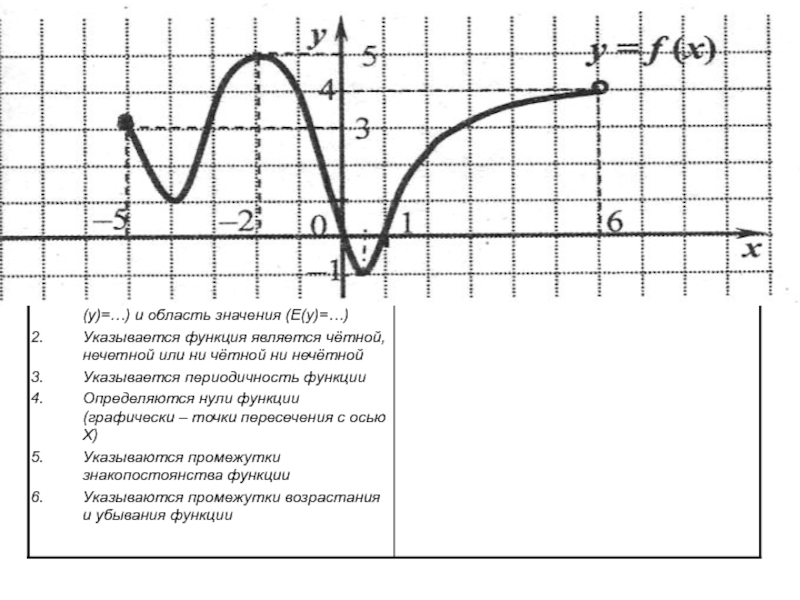
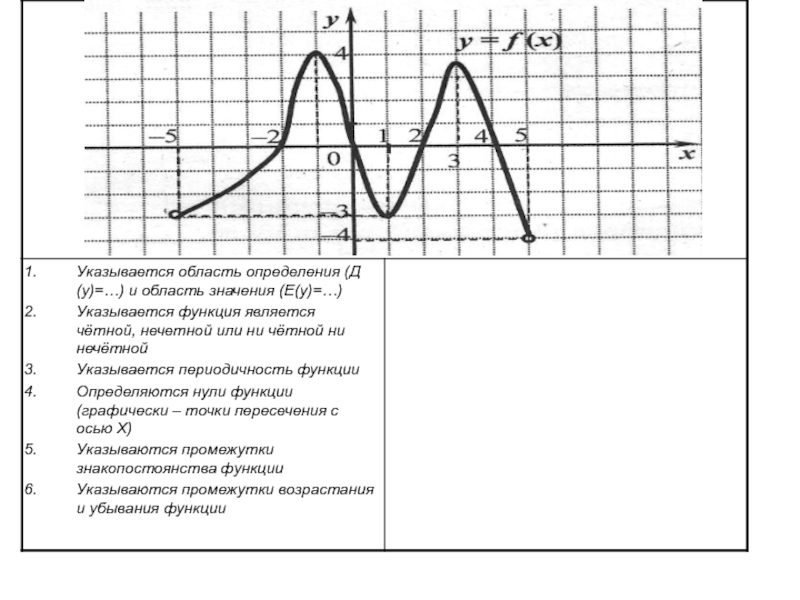
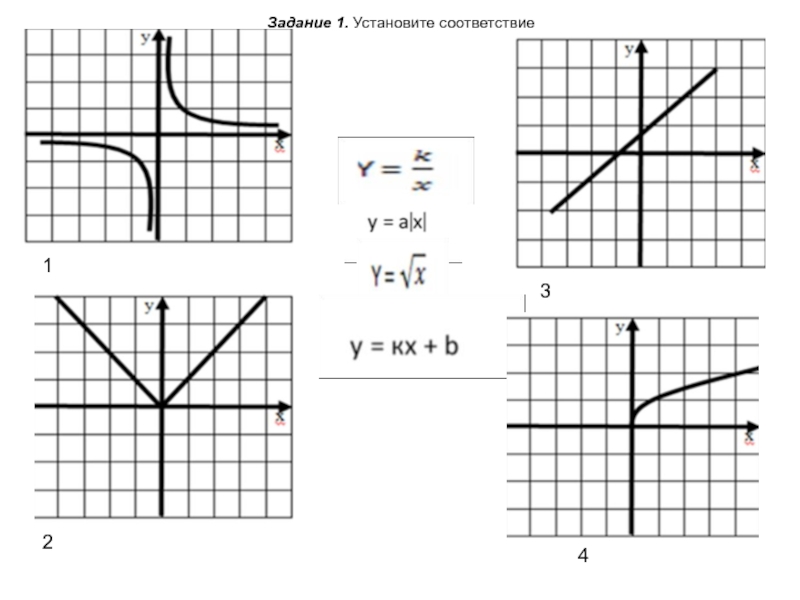
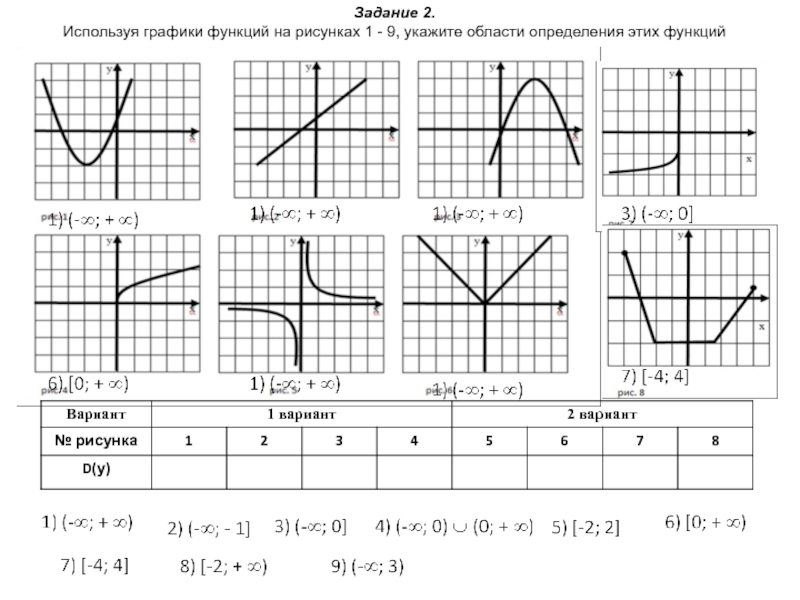
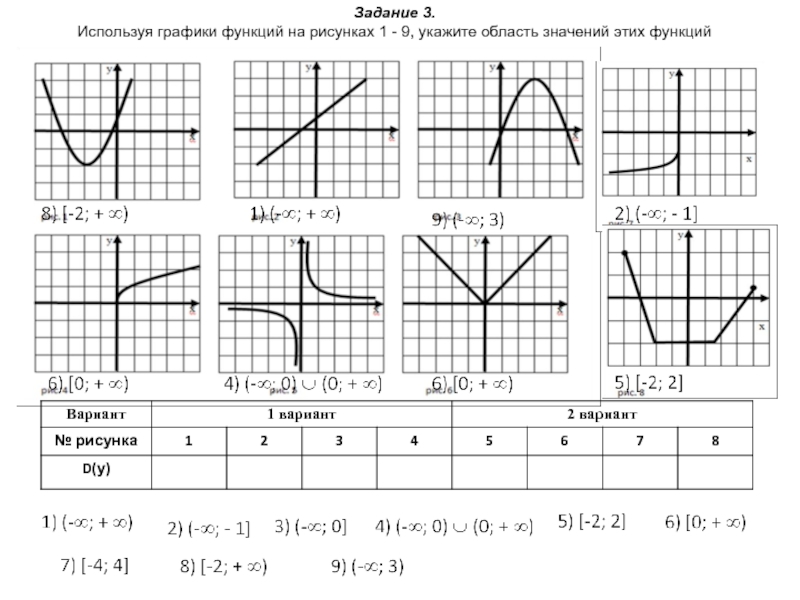
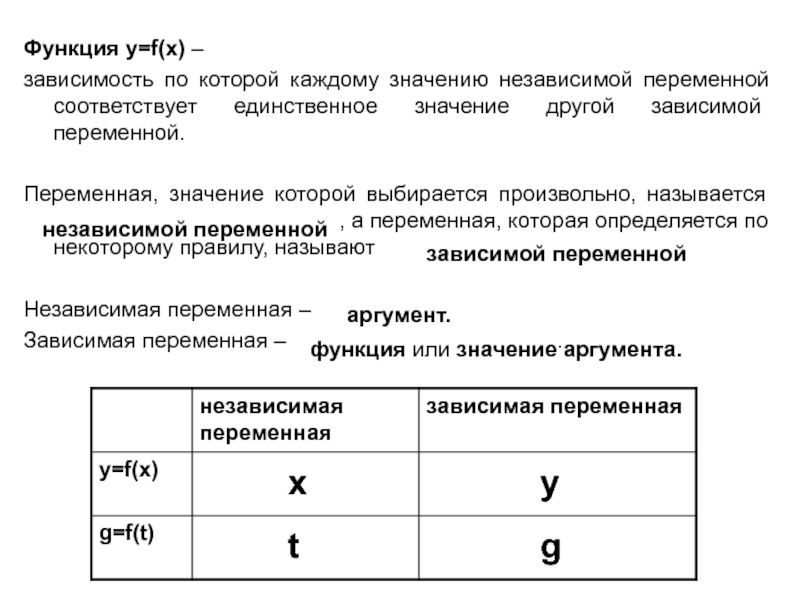
соответствует единственное значение другой зависимой переменной.
Переменная, значение которой выбирается произвольно,
называется независимой переменной, а переменная, которая определяется по некоторому правилу, называют зависимой переменной.Независимая переменная –
Зависимая переменная – .
аргумент.
функция или значение аргумента.
у
g
x
t
независимой переменной
зависимой переменной




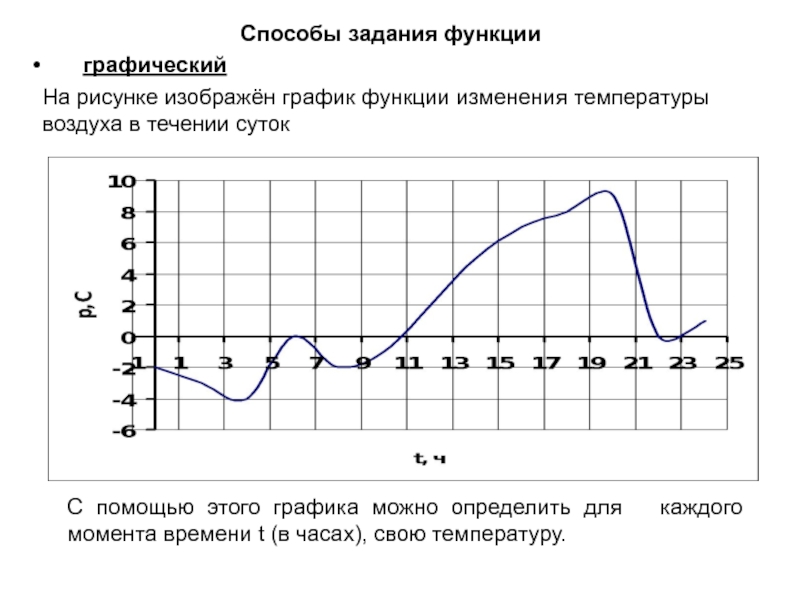


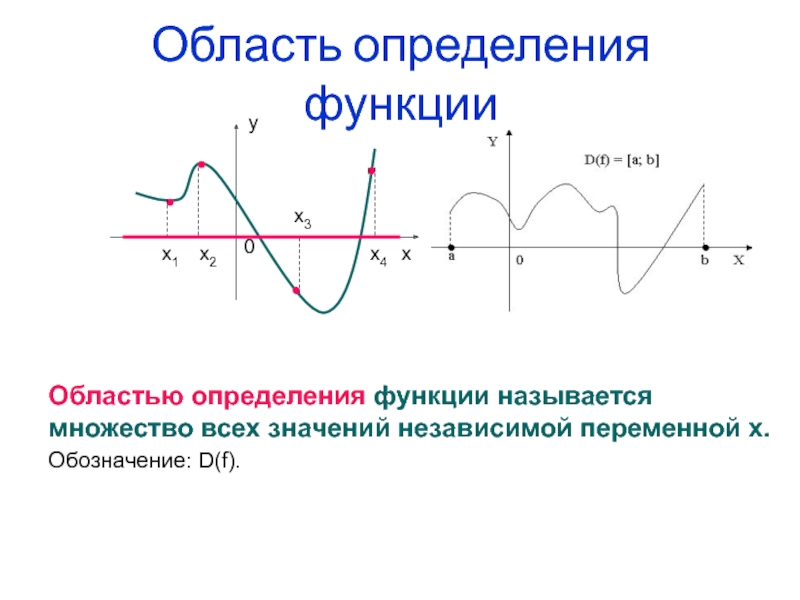
![Функция у=f(x) 4-4D(f) x[-4;4]Найдите область определения функции 4-4D(f) x[-4;4]Найдите область определения функции](/img/thumbs/fd92b4a0621f2fdb5b784360060c6680-800x.jpg)
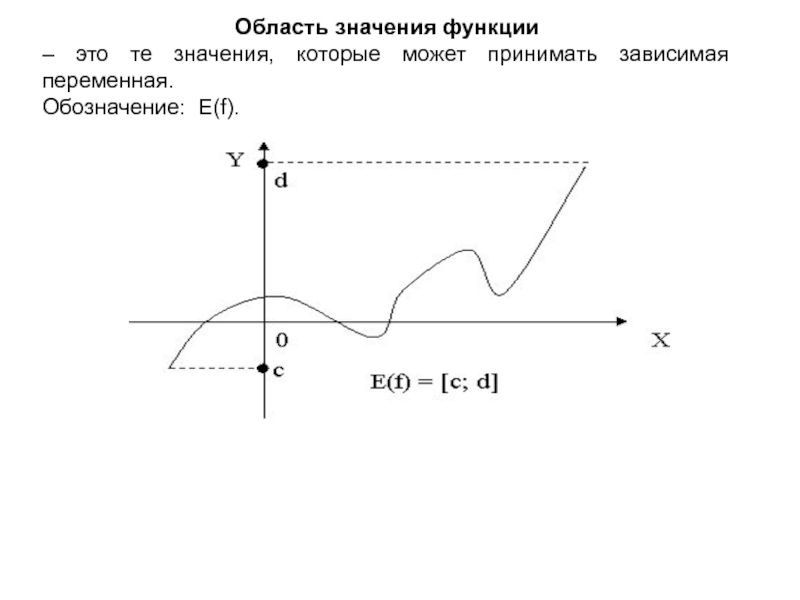
![Функция у=f(x) -2 2E(f) x[-2;2]Найдите область значения функции -2 2E(f) x[-2;2]Найдите область значения функции](/img/thumbs/9c34e48dc0cafadb0395ed3758c1f57a-800x.jpg)

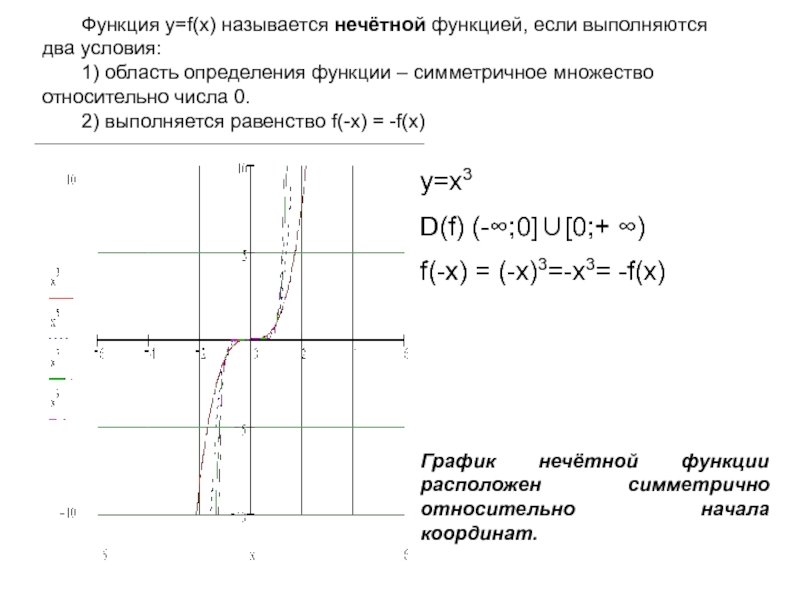

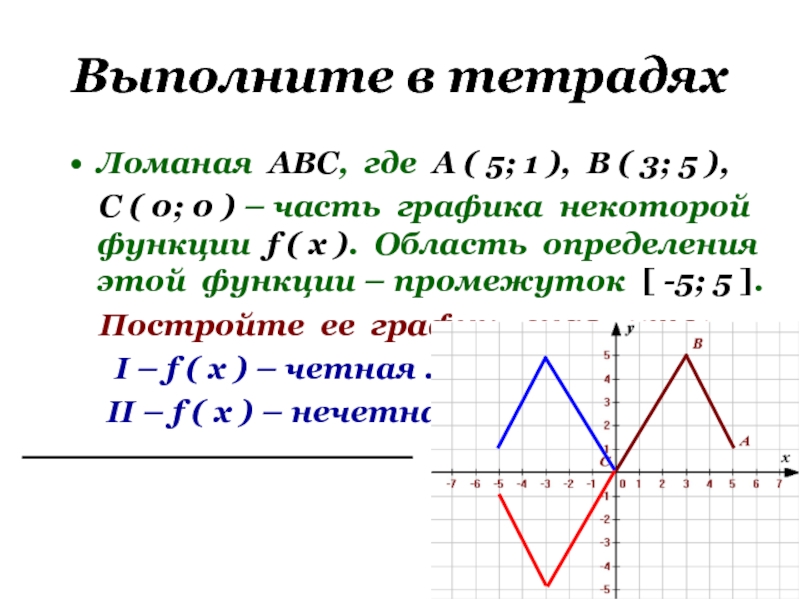

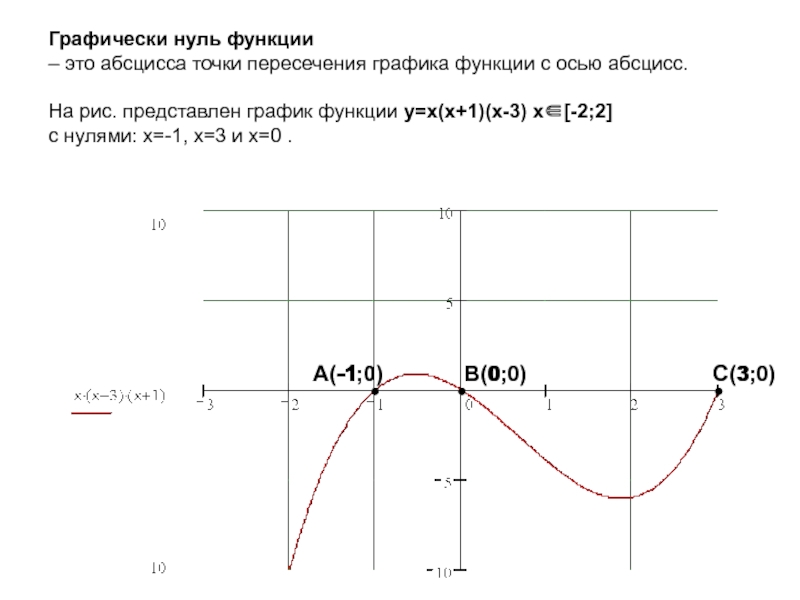
![Функция у=f(x) Промежутки знакопостоянства функции – это промежутки, на которых функция сохраняет (не Промежутки знакопостоянства функции – это промежутки, на которых функция сохраняет (не меняет) знак.y=x(x+1)(x-3) D(f): x[-2;2]y>0 при y](/img/thumbs/9e356bb208c8d40ea118c96fc251a4cb-800x.jpg)

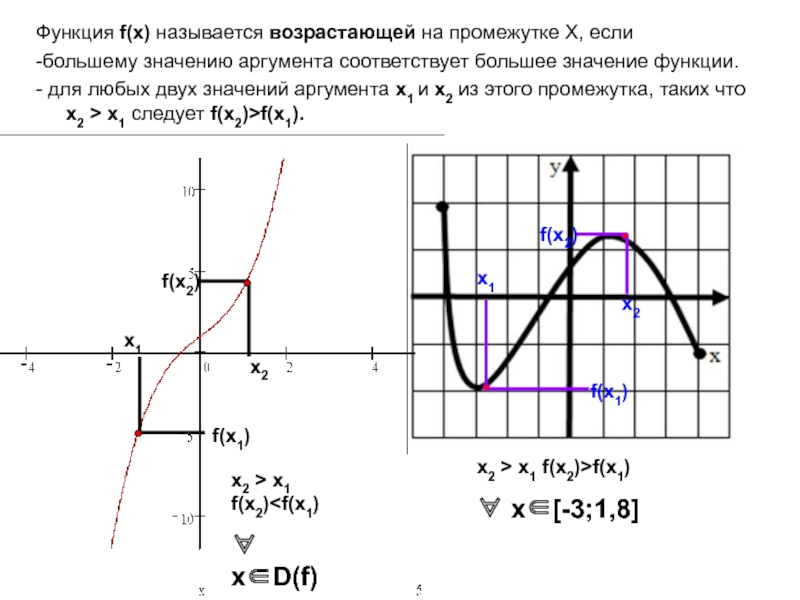
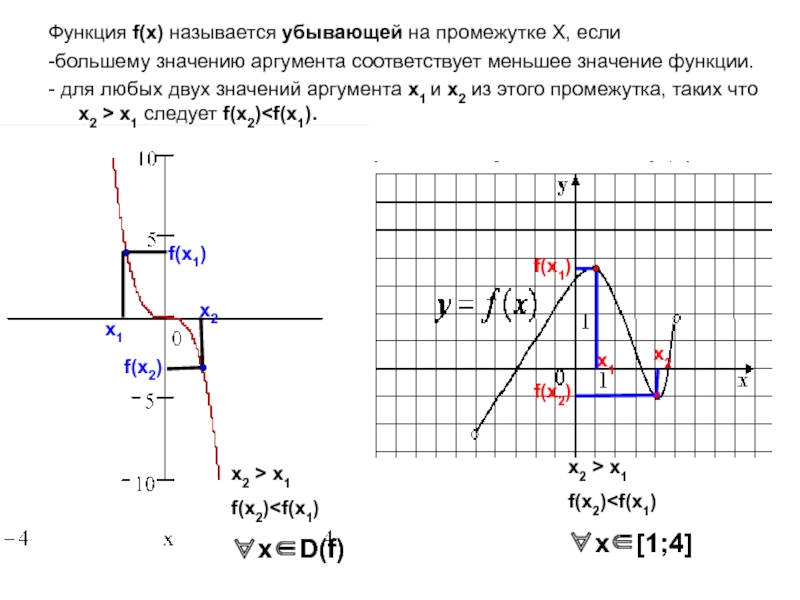
![Функция у=f(x) Задание 4. По графику функции определите промежутки монотонности функцийФункция возрастаетФункция возрастаетФункция Задание 4. По графику функции определите промежутки монотонности функцийФункция возрастаетФункция возрастаетФункция убываетФункция убываетx[3;5]x[-5;-3]x [-3;-1] и x [2;3]x](/img/thumbs/7ae4f98e7a3eba2d1f4d721e0ab8abc9-800x.jpg)