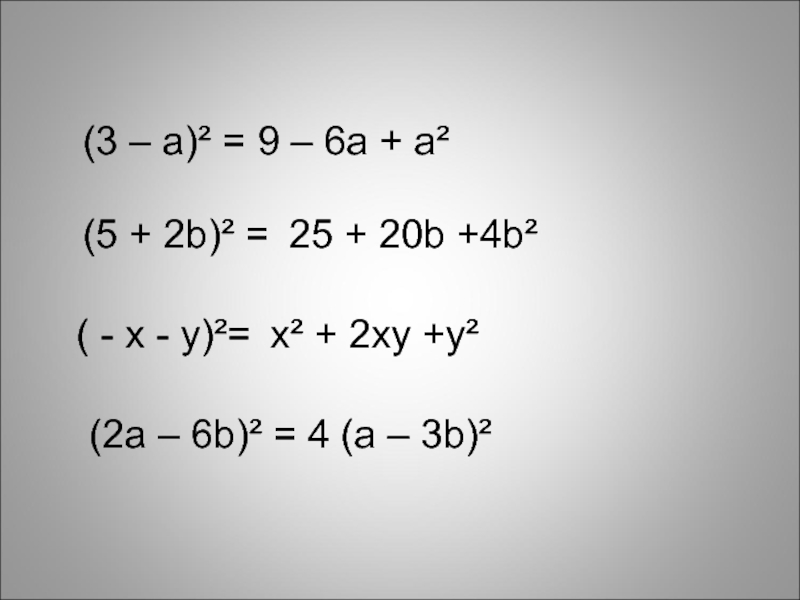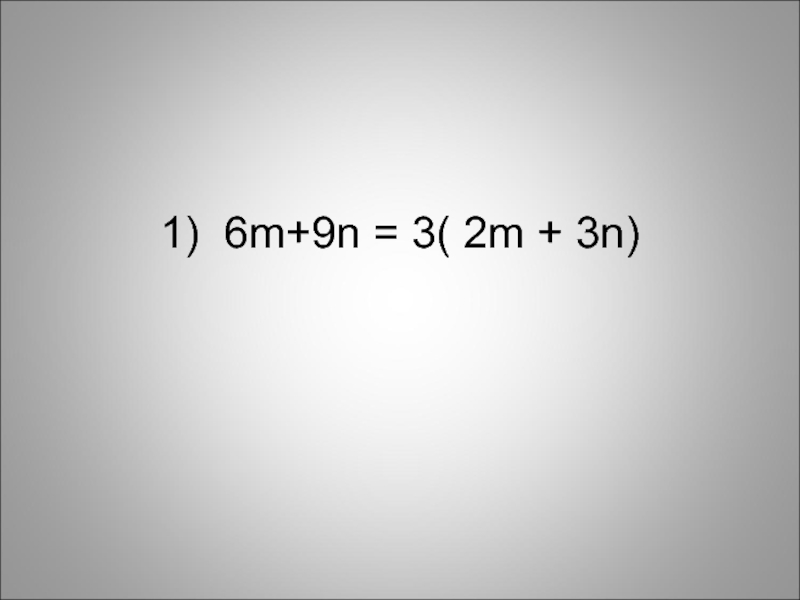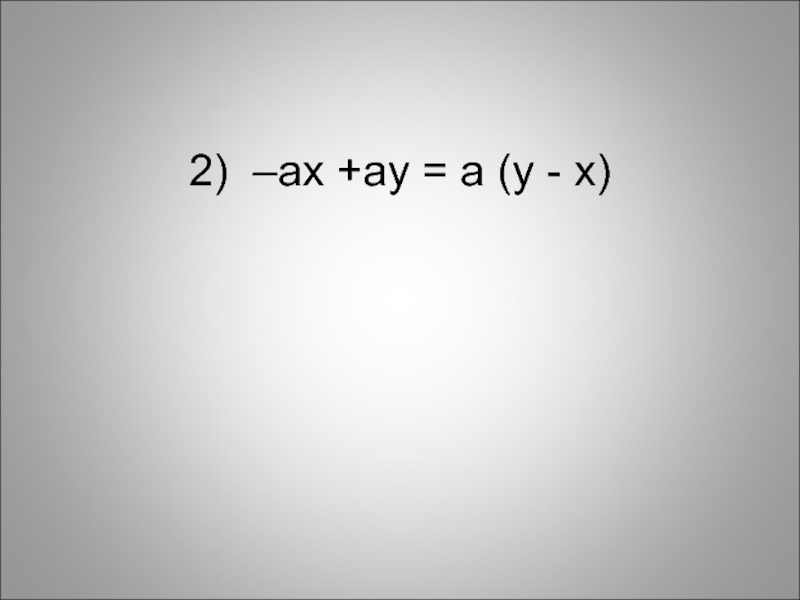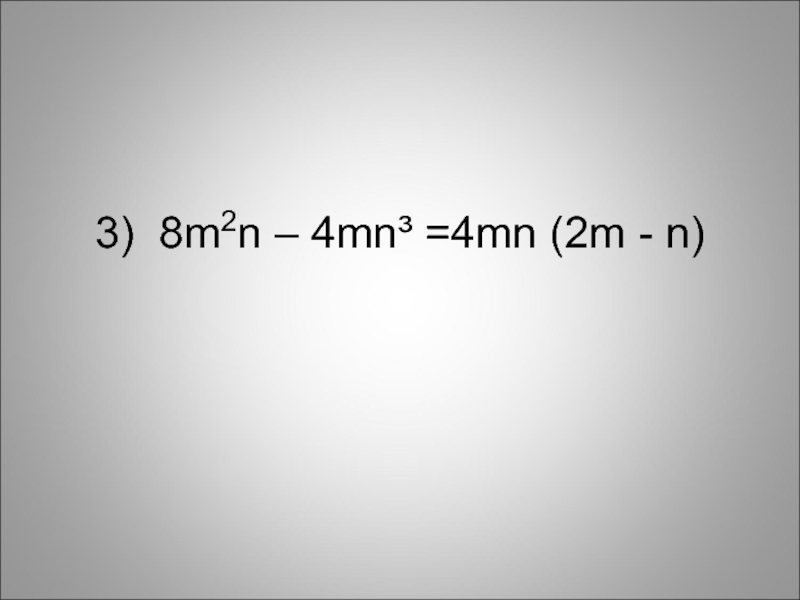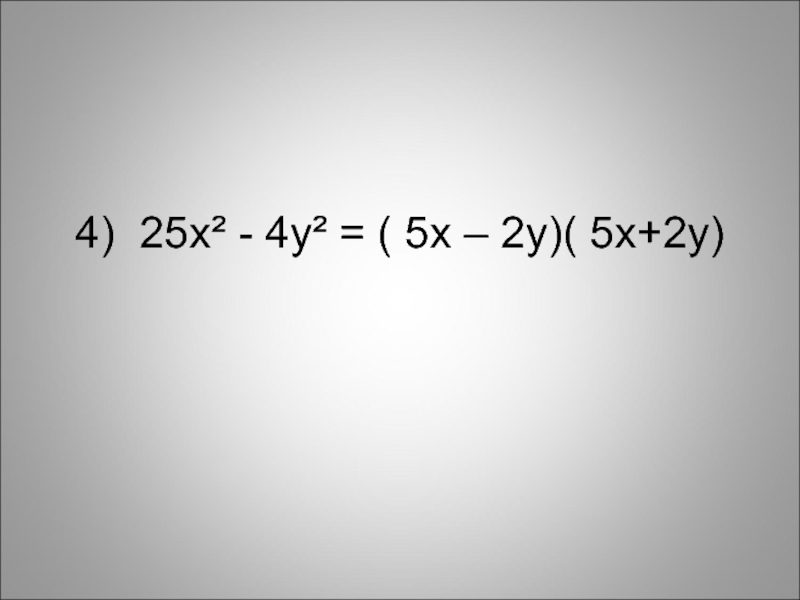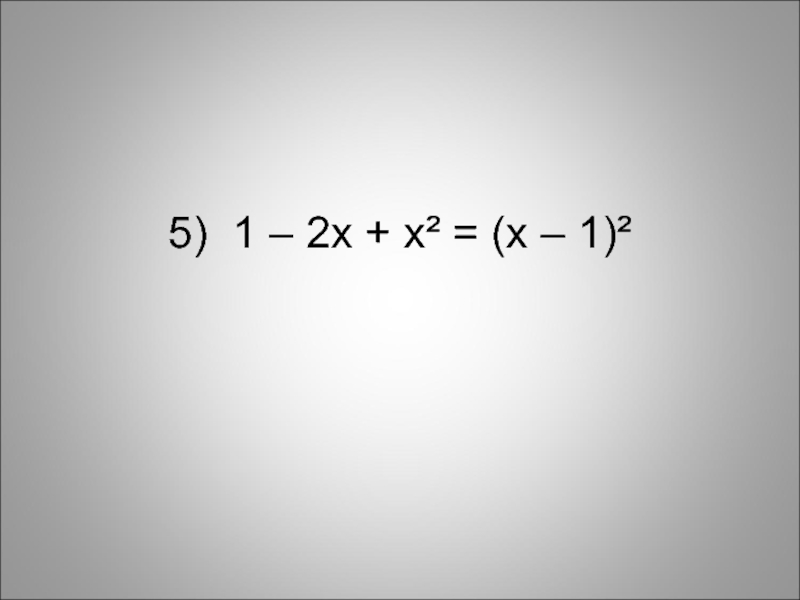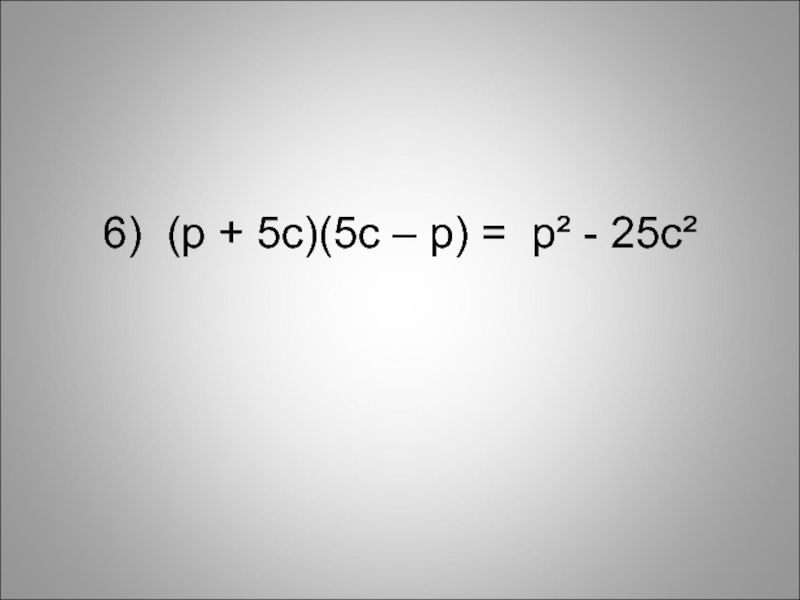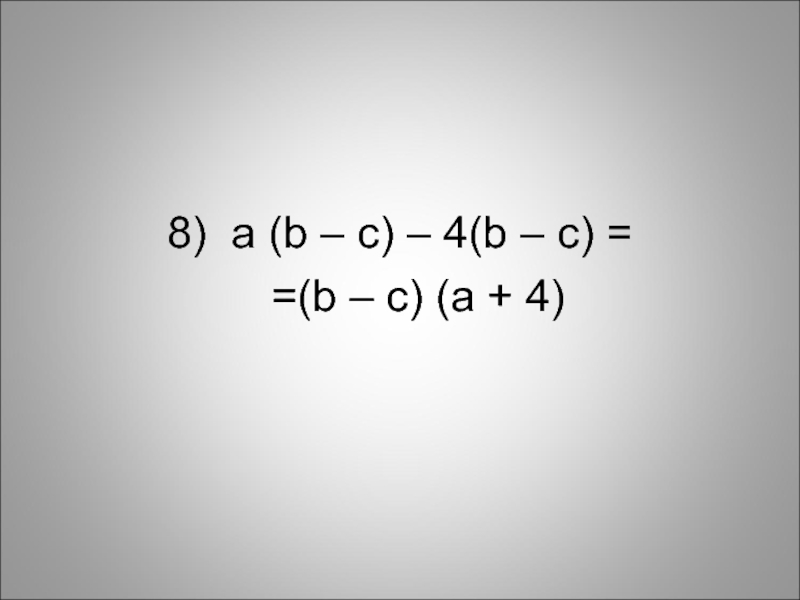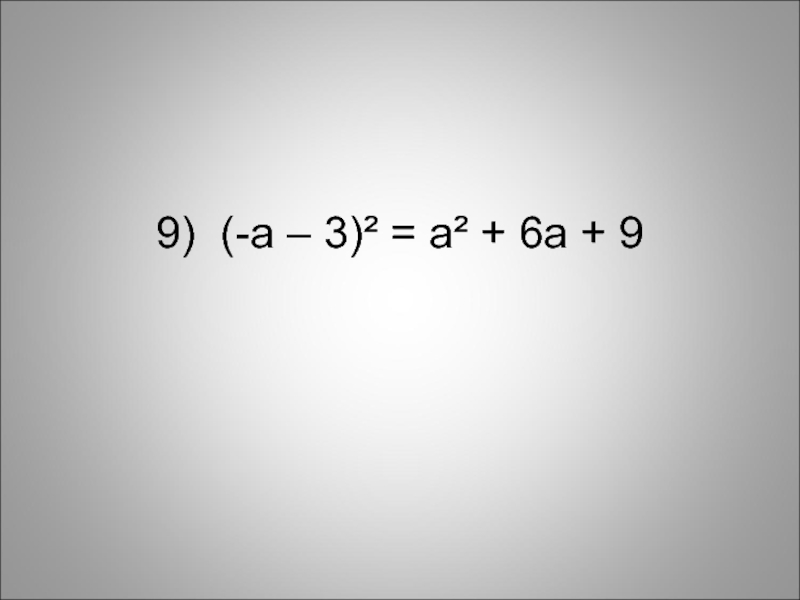Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Разложение многочленов на множители
Содержание
- 1. Разложение многочленов на множители
- 2. Три пути ведут к знанию: путь размышления
- 3. Способы разложения многочлена на множителиВынесение общего множителя за скобкиСпособ группировкиФормулыПрименение нескольких способов разложения
- 4. Представление многочлена в виде произведения одночлена и
- 5. Вынесение общего множителя Из каждого слагаемого,
- 6. общим множителем может быть не
- 7. Формулыa² - b² = (a – b)
- 8. (3 – a)² =9 – 6a +
- 9. Способ группировки. выполнить группировку слагаемых, имеющих общий
- 10. Алгоритм разложения многочлена на множителиВынести общий множитель
- 11. Графический диктантЕсли согласен, ставиШЬ знак
- 12. 1) 6m+9n = 3( 2m + 3n)
- 13. 2) –ax +ay = a (y - x)
- 14. 3) 8m2n – 4mn³ =4mn (2m - n)
- 15. 4) 25x² - 4y² = ( 5x – 2y)( 5x+2y)
- 16. 5) 1 – 2x + x² = (x – 1)²
- 17. 6) (p + 5c)(5c – p) = p² - 25c²
- 18. 7) 4a² + 12ab + 9b² = (2a + 3b)²
- 19. 8) a (b – c)
- 20. 9) (-а – 3)² = а² + 6а + 9
- 21. Слайд 21
- 22. А. Задания нормативного уровня. 1) 2x²
- 23. Б. Задания компетентного уровня 1) a²b³ -
- 24. С. Задания творческого уровня 1) 125 a³
- 25. Мое мнение: На уроке : Было трудно …Было интересно …Я научился … Меня удивило …
- 26. Скачать презентанцию
Три пути ведут к знанию: путь размышления – это путь самый благородный, путь подражания – это самый легкий и путь опыта – это путь самый горький.
Слайды и текст этой презентации
Слайд 1Разложение многочленов на множители
Бращенкова Надежда Александровна
Учитель математики
ГБОУ СОШ №
450
Слайд 2
Три пути ведут к знанию:
путь размышления – это путь
самый благородный,
путь подражания – это самый легкий и
путь
опыта – это путь самый горький. Конфуций
Слайд 3Способы разложения многочлена на множители
Вынесение общего множителя за скобки
Способ группировки
Формулы
Применение
нескольких способов разложения
Слайд 4Представление многочлена в виде произведения одночлена и многочленов называется …
разложением многочлена на множители
2a-3d
5х( -6+у)
(9а-5в) ( 3х-4у)
-4х (-6ху)
Слайд 5Вынесение общего множителя
Из каждого слагаемого, входящего в многочлен,
выносится некоторый одночлен, входящий в качестве множителя во все слагаемые
5х
-15у =5 (х – 3у)
3х² + х =
х (3х + 1)
15у – 25у² =
5у(3 – 5у)
Слайд 6 общим множителем может быть
не только одночлен, но
и многочлен.
2х (а - 4) + (а - 4)
=( х + 5у) – 12х ( 5у + х) =
(а – 4) (2х + 1)
(х + 5у)(1 – 12х)
2а (в - 3с) + 5с(3с – в)=
(в – 3с) (2а – 5с)
Слайд 7Формулы
a² - b² = (a – b) (a+b)
a² - 2ab
+ b² = ( a – b)²
a² + 2ab +
b² = ( a + b)²a³ + b³ = ( a + b) ( a² - ab + b² )
a³ - b³ = ( a - b) ( a² + ab + b² )
Слайд 8
(3 – a)² =
9 – 6a + a²
(5 + 2b)²
=
25 + 20b +4b²
( - x - y)²=
x² +
2xy +y²(2a – 6b)² =
4 (a – 3b)²
Слайд 9Способ группировки.
выполнить группировку слагаемых, имеющих общий множитель;
отдельно в
каждой группе найти общий множитель и вынести его за скобки;
в
получившемся выражении найти общий множитель и вынести его за скобки. Слайд 10Алгоритм разложения многочлена на множители
Вынести общий множитель за скобки (если
он есть).
Попробовать разложить многочлен на множители по формулам сокращенного умножения.
Попытаться
применить способ группировки (если предыдущие способы не привели к цели). Слайд 11Графический диктант
Если согласен, ставиШЬ знак
,
если нет
В результате получается
графическое изображение.Слайд 22А. Задания нормативного уровня.
1) 2x² + 4xy + 2y²
=2(x + y)²
2) 3m² - 27n² = 3(m – 3n)(m
+ 3n)3) (a + b)c² - 4(a+ b) = (a + b)(c - 2)(c +2 )
4) 7а-7в+ аn – b n = (а – в)(7 + n)
5) x y+ 2y+2x+4 = (у + 2)(х + 2)
6) y2a-y2b+x2 a- x2b = (а – в)(у2 + х2)
Слайд 23Б. Задания компетентного уровня
1) a²b³ - a²b - b³+ b
= a²b(b² -1)– b(b² -1) = =b(b² -1)(a² -1) =
b(b –1)(b +1)(a –1)(a+1)2) a² + c – a - c² = ( a – c)(a + c – 1)
3) (x² + 4y²)² - 16x²y² = (x² + 4y² - 4xy)( x²+ + 4y² +4xy) = (x - 2y)²(x + 2y)²
4) x y+ 2y-2x-4 = (х + 2)(у – 2)
5) 2сх – су – 6х + 3у = (2х – у)(с – 3)
6) х2 +x y+ xy2+y3 = (х + у)(х + у2)
Слайд 24С. Задания творческого уровня
1) 125 a³ + 8 = (
5a + 2)( 25a² - 10a + 4)
2) (a +
1)³ - ( a + 1)=a (a + 1)( a + 2)3) 4b²c² - b² - 2bc - c² = (2bc – b – c)( 2bc + b + c)
4) x4 +x3y- xy3-y4 = (х +у)(х3 – у3)
5) ху2 – ву2 – ах + ав + у2 – а = (у2 – а)(х – в + 1)
6) х2 – 3х + 6 – 2х = (х – 2)(х – 3)