Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория графов 6 класс
Содержание
- 1. Теория графов 6 класс
- 2. Что такое теория графов?Теория графов – это
- 3. Теория графов находит применение, например, в геоинформационных
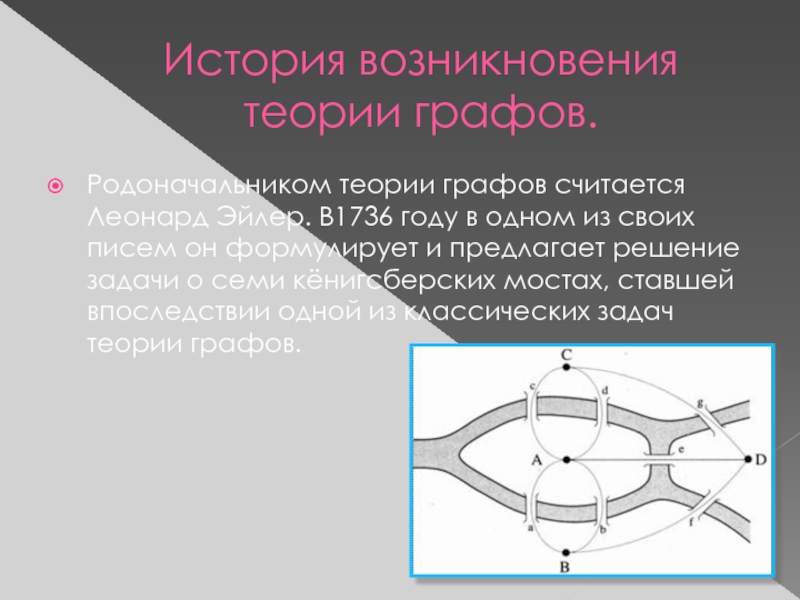
- 4. История возникновения теории графов.Родоначальником теории графов считается
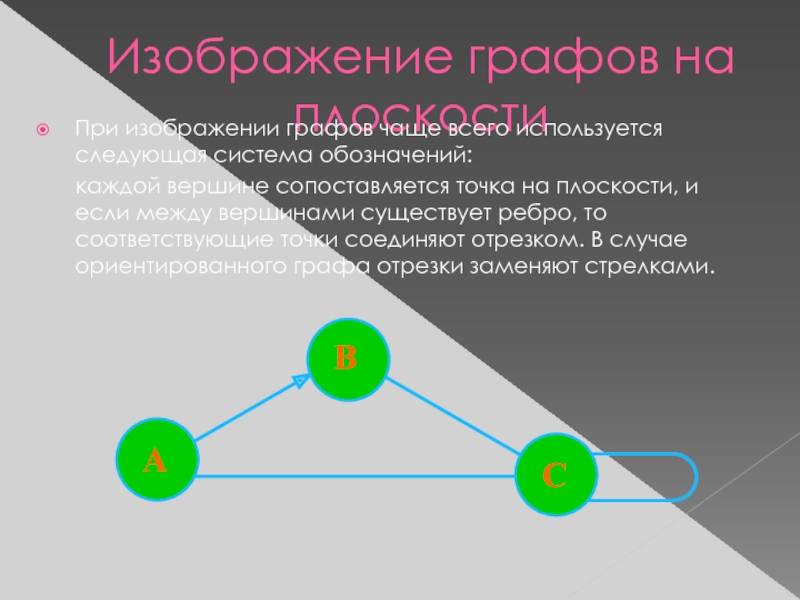
- 5. Изображение графов на плоскостиПри изображении графов чаще
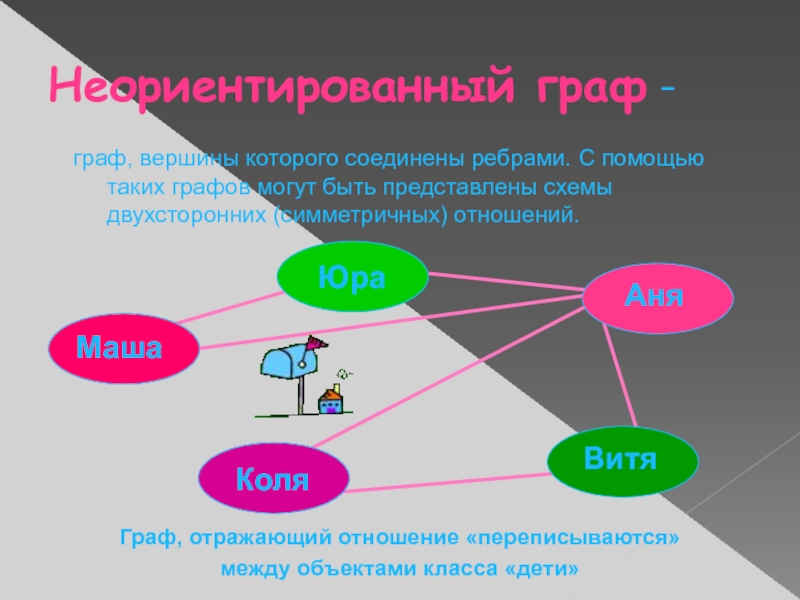
- 6. Неориентированный граф - граф, вершины которого соединены
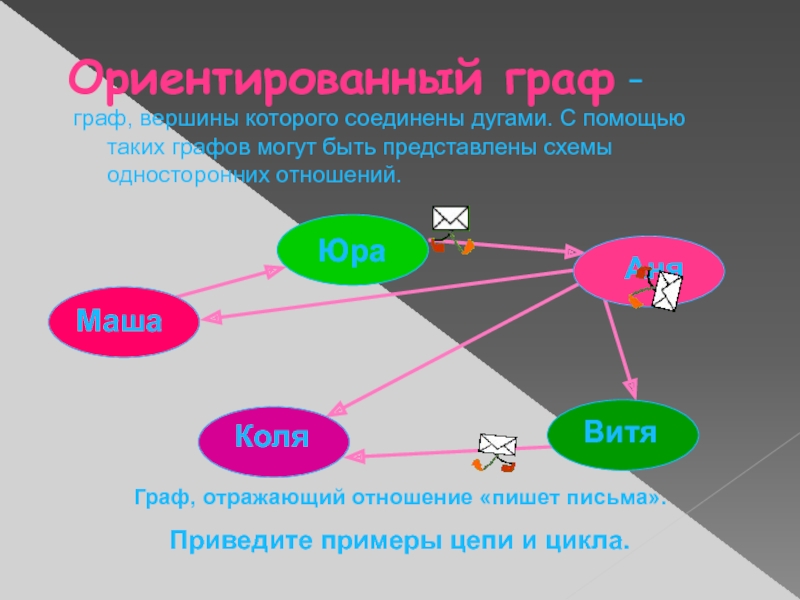
- 7. Ориентированный граф - граф, вершины которого соединены
- 8. граф, у которого вершины или рёбра (дуги)
- 9. Дерево – граф иерархической структуры. Между любыми
- 10. Задача «Подружки»У трёх подружек - Ксюши,
- 11. 1. Костюм и шапочка Насти одного цвета.2.
- 12. Три учительницы - Ирина Васильевна, Дарья Михайловна
- 13. И.В. Д.М. С.П.Яр.Вл.Кр.хим.биол.физ. 1. И.В. работает не
- 14. Теория графов и анализ художественного текстаДавайте определим,
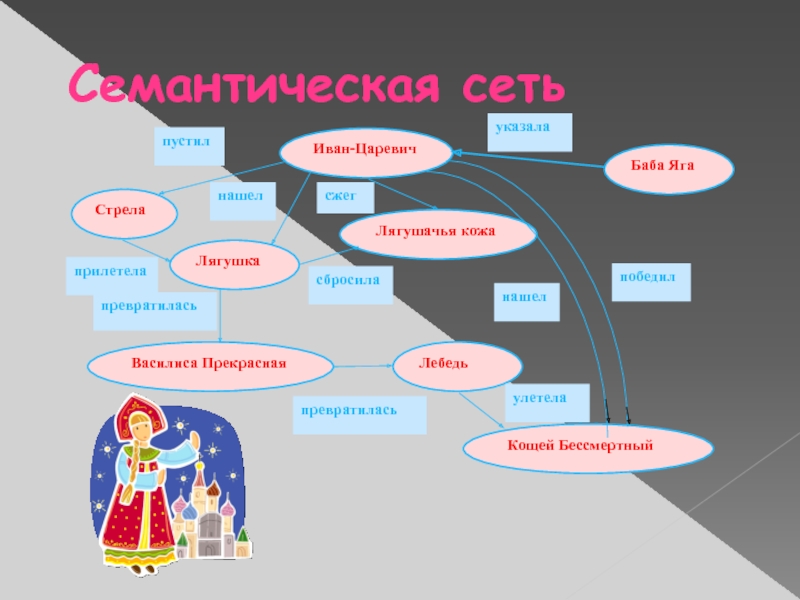
- 15. Семантическая сеть
- 16. В прозаических произведениях Пушкина преобладают краткие фразы,
- 17. Деревья лермонтовской прозы во многом похожи на
- 18. Признаки И.Л. СевбоА теперь выясним; по какому
- 19. Проведём эксперимент. Перед нами строки из произведения
- 20. Слайд 20
- 21. Из данных таблицы ясно, что дерево на
- 22. выводыТеория графов помогает решать логические задачи.С помощью
- 23. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3Теория графов находит применение, например, в геоинформационных системах (ГИС).
Существующие или
вновь проэктируемые дома, сооружения, кварталы и т.п. рассматриваются как вершины,
а соединяющие их дороги, инженерные сети и т.п. – как рёбра. Применение различных вычислений, производимых на таком графе, позволяет, например, найти кратчайший объездной путь или ближайший продуктовый магазин, спланировать оптимальный маршрут.Слайд 4История возникновения теории графов.
Родоначальником теории графов считается Леонард Эйлер. В1736
году в одном из своих писем он формулирует и предлагает
решение задачи о семи кёнигсберских мостах, ставшей впоследствии одной из классических задач теории графов.Слайд 5Изображение графов на плоскости
При изображении графов чаще всего используется следующая
система обозначений:
каждой вершине сопоставляется точка на плоскости, и если между
вершинами существует ребро, то соответствующие точки соединяют отрезком. В случае ориентированного графа отрезки заменяют стрелками.Слайд 6Неориентированный граф -
граф, вершины которого соединены ребрами. С помощью
таких графов могут быть представлены схемы двухсторонних (симметричных) отношений.
Граф, отражающий
отношение «переписываются» между объектами класса «дети» Слайд 7Ориентированный граф -
граф, вершины которого соединены дугами. С помощью
таких графов могут быть представлены схемы односторонних отношений.
Маша
Юра
Аня
Витя
Коля
Граф, отражающий отношение
«пишет письма».Приведите примеры цепи и цикла.
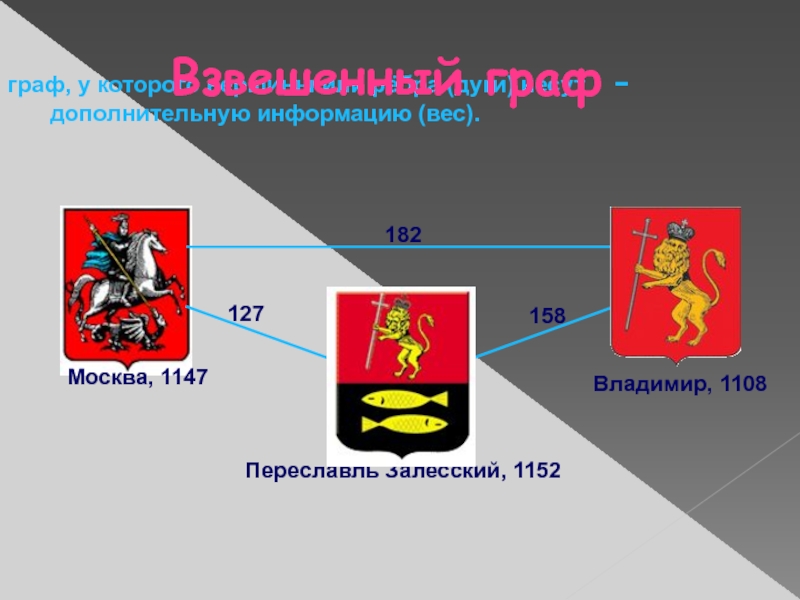
Слайд 8граф, у которого вершины или рёбра (дуги) несут дополнительную информацию
(вес).
Москва, 1147
Переславль Залесский, 1152
Владимир, 1108
Взвешенный граф -
182
158
127
Слайд 9Дерево – граф иерархической структуры. Между любыми двумя его вершинами
существует единственный путь. Дерево не содержит циклов и петель.
Слайд 10Задача «Подружки»
У трёх подружек - Ксюши, Насти и Оли
- новогодние карнавальные костюмы белого, фиолетового и синего цветов, и
шапочки тех же цветов. У Насти цвет костюма и шапочки совпали, у Ксюши ни костюм, ни шапочка не были фиолетового цвета, а Оля была в белой шапочке, но цвет костюма у неё не был белым.Как были одеты девочки?
Решение:
Будем изображать множество подружек, шапочек и костюмов прямоугольниками, а элементы множеств - точками, помещенными в эти прямоугольники.
Слайд 111. Костюм и шапочка Насти одного цвета.
2. Костюм и шапочка
Ксюши не фиолетового цвета.
3. Оля в белой шапочке.
4. Костюм у
Оли не белый.подружки
костюмы
шапочки
Ксюша Оля Настя
Бел.
Фиол.
Син.
Бел.
Фиол.
Син.
Ксюша не в фиолетовой шапочке и не в белой, значит, в синей, а у Насти – фиолетовая шапочка.
У Насти цвета шапочки и костюма совпадают по условию, а у Оли – не совпадают.
Вывод: Настя в фиолетовом костюме и шапочке,
Ксюша в белом костюме и синей шапочке,
Оля в синем костюме и белой шапочке.
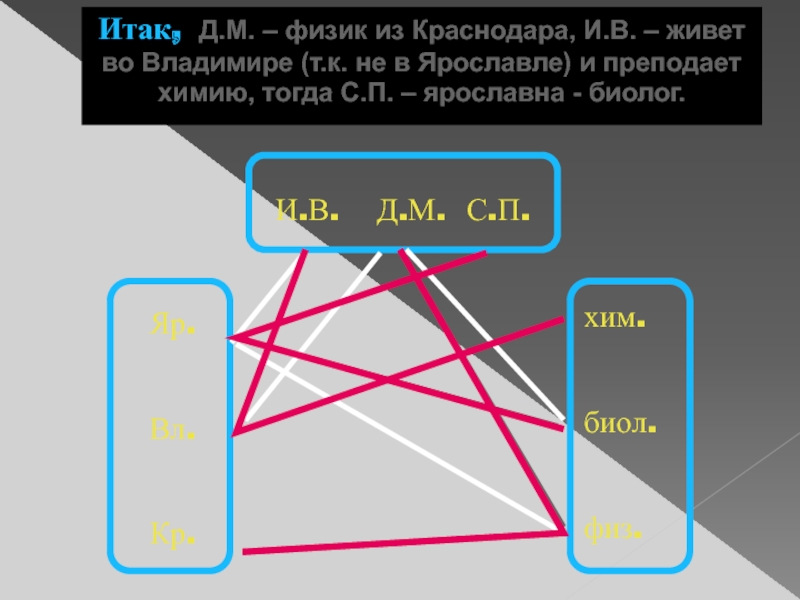
Слайд 12Три учительницы - Ирина Васильевна, Дарья Михайловна и Софья Петровна
- преподают химию, биологию и физику в школах Ярославля, Владимира
и Краснодара. Известно, чтоИ.В. работает не в Ярославле, а Д.М. - не во Владимире;
та, которая живет в Ярославле, преподает не физику;
работающая во Владимире – учитель химии;
Д.М. преподает не биологию.
Кто в каком городе живет и какой предмет преподает?
Задача «Учительницы»
Слайд 13
И.В. Д.М. С.П.
Яр.
Вл.
Кр.
хим.
биол.
физ.
1. И.В. работает не в Ярославле, а
Д.М. - не во Владимире;
та, которая живет в Ярославле,
преподает не физику;3. работающая во Владимире – учитель химии;
4. Д.М. преподает не биологию.
Вывод: Д.М. не биолог и не химик, следовательно, преподает физику.
Вывод: в Ярославле живет учитель биологии (т.к. не физика и не химия), тогда физик - в Краснодаре.
Итак, Д.М. – физик из Краснодара, И.В. – живет во Владимире (т.к. не в Ярославле) и преподает химию, тогда С.П. – ярославна - биолог.
Слайд 14Теория графов и анализ художественного текста
Давайте определим, как фразы одного
писателя или поэта отличаются от других. А точнее, при анализе
художественного текста можно использовать математические методы. Покажем на примере творчества нескольких писателей, как на язык деревьев переводятся трудноуловимые, и на первый взгляд неформализуемые особенности стиля, которые кладутся в основу стилистической диагностики. Например, основная черта синтаксиса А.С. Пушкина – её ритмизованность и подчинённый ей лаконизм выражений.Слайд 16В прозаических произведениях Пушкина преобладают краткие фразы, часто встречаются нераспространенные
предложения. Так если взять «Капитанскую дочку», то для неё типично
расположенное дерево подчинения следующего вида:Пушкинский текст в основном состоит из предложений, в которых не более 11 слов, а рисунки этих деревьев либо симметричны, либо имеют длинный правый отросток. При этом даже для длинных фраз громоздкие деревья практически не возникают. Как мы видим, интуитивное ощущение прозаичности пушкинской фразы соответствует строгому понятию синтаксической простоты.
Слайд 17Деревья лермонтовской прозы во многом похожи на пушкинские, хотя расчёты
показывают, что в среднем предложения Лермонтова чуть-чуть длиннее и чуть-чуть
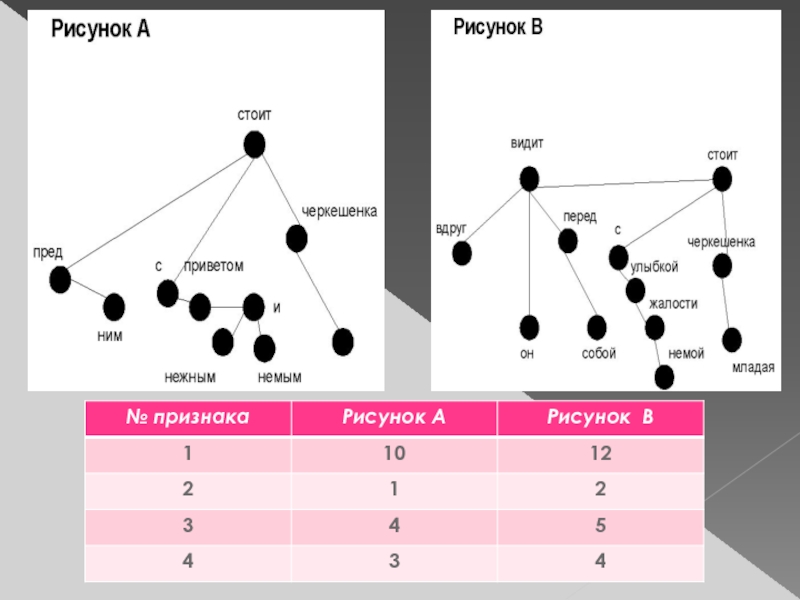
сложнее. Впрочем, есть важное различие в рисунках деревьев, свойственных этим авторам. Ширина ветвления корня дерева для фразы из «Героя нашего времени» гораздо больше, чем для фразы из «Капитанской дочки». Это означает, что дерево лермонтовской фразы растёт вширь, в то время как в пушкинской фразе оно растёт вглубь. Большая ширина ветвления возникает вследствие того, что сказуемые в лермонтовской фразе подчиняют себе не только дополнения, но и разнообразные по структуре и значению обстоятельства.Слайд 18Признаки И.Л. Севбо
А теперь выясним; по какому принципу лингвисты проводят
анализ художественного текста. И.Л. Севбо привёл 7 таких признаков, мы
приведём для примера 4.1. Количество узлов дерева (т.е. количество слов во фразе).
2. Количество простых предложений в сложном (помечание стрелок, соответствующих связям между частями сложного предложения)
3. Число уровней в дереве (длина самого длинного из путей дерева)
4. Ширина ветвления корня (число узлов подчинённых корню)