Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
УРАВНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ И ЕГО ГРАФИК
Содержание
- 1. УРАВНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ И ЕГО ГРАФИК
- 2. ЭПИГРАФУРАВНЕНИЯ – ЭТО ЗОЛОТОЙ КЛЮЧ, ОТКРЫВАЮЩИЙ ВСЕМАТЕМАТИЧЕСКИЕ
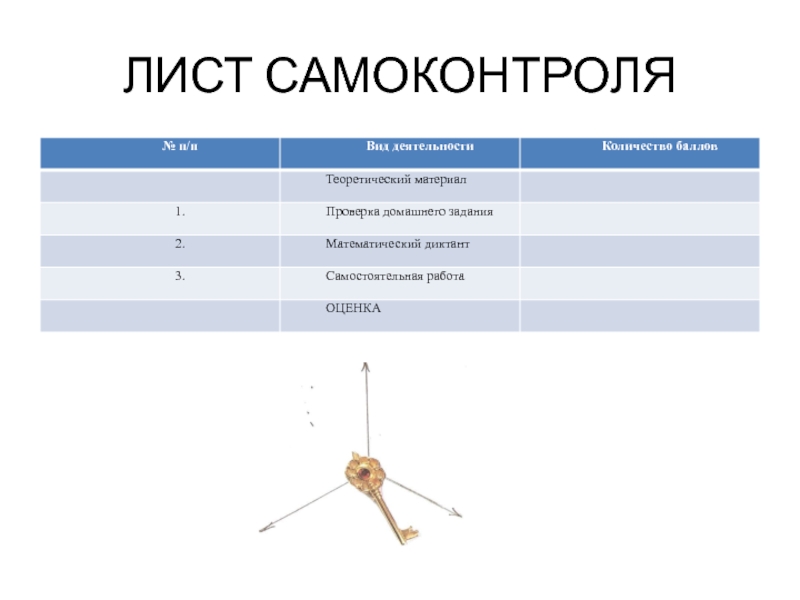
- 3. ЛИСТ САМОКОНТРОЛЯ
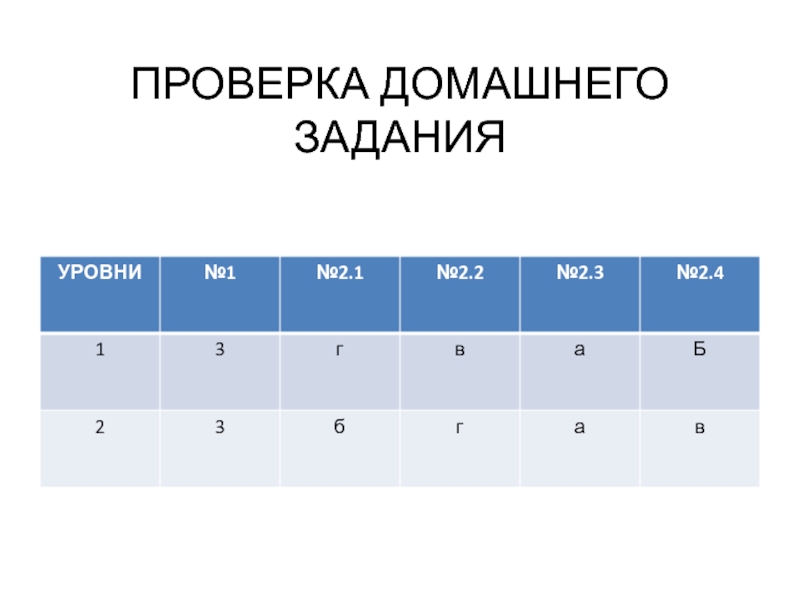
- 4. ПРОВЕРКА ДОМАШНЕГО ЗАДАНИЯ
- 5. Ответьте на вопросыЧто называют решением уравнения с
- 6. Ответьте на вопросы5. Что представляют собой графики
- 7. Математический диктанту + х2 = 0х2 +
- 8. Взаимопроверка Парабола.Окружность с центром в точке (0;
- 9. 1. ОПРЕДЕЛИТЕ,является ли решением уравнения х
- 10. 2. ПОСТРОЙТЕ ГРАФИК УРАВНЕНИЯХ У = 6
- 11. САМОСТОЯТЕЛЬНАЯ РАБОТА
- 12. ДОМАШНЕЕ ЗАДАНИЕП.17 ПОВТОРИТЬ ОПРЕДЕЛЕНИЯ И
- 13. ГРАФИКИ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ ДЕКАРТОВ ЛИСТх2
- 14. КЛОФОИДА«Клофо» – от греч. «прясть». Клофоида
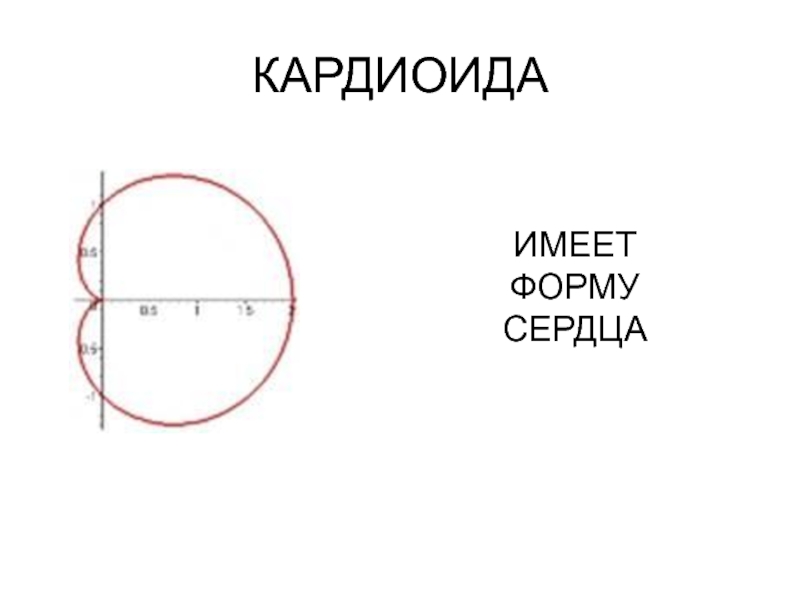
- 15. КАРДИОИДАИМЕЕТ ФОРМУ СЕРДЦА
- 16. СТАТИСТИЧЕСКИЙ ОТЧЁТ4,5 - 5 баллов -
- 17. ЖЕЛАЮ УДАЧИДО СКОРОЙ ВСТРЕЧИ ПРИ ИЗУЧЕНИИ ТЕМЫ «ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ СИСТЕМ УРАВНЕНИЙ»
- 18. Скачать презентанцию
ЭПИГРАФУРАВНЕНИЯ – ЭТО ЗОЛОТОЙ КЛЮЧ, ОТКРЫВАЮЩИЙ ВСЕМАТЕМАТИЧЕСКИЕ СЕЗАМЫ С.
Слайды и текст этой презентации
Слайд 5Ответьте на вопросы
Что называют решением уравнения с двумя переменными?
Важен ли
в этой паре порядок записи значений переменных?
Дайте определение графика уравнения
с двумя переменными.Что является графиком линейного уравнения с двумя переменными?
Слайд 6Ответьте на вопросы
5. Что представляют собой графики уравнений второй степени
с двумя переменными?
6. От чего зависит вид графика уравнения второй
степени с двумя переменными?7. Как определить вид графика уравнения второй степени с двумя переменными?
Слайд 8Взаимопроверка
Парабола.
Окружность с центром в точке (0; - 2)
и R = 3.
3. Прямая.
4. Гипербола.
5.
Точка (3; - 2).
Слайд 91. ОПРЕДЕЛИТЕ,
является ли решением уравнения
х – у2
– 1 = 0 пара чисел
а) (0; -1); в) (1;1);б) (2; -1); г) (5; - 2).
-
Слайд 11САМОСТОЯТЕЛЬНАЯ РАБОТА
№ 402 (учебник)
а) у – 0, 5 х2
= 1б) х2 + у2 = 9
в) (х + 1)2 + (у – 1)2 = 4
Слайд 12ДОМАШНЕЕ ЗАДАНИЕ
П.17 ПОВТОРИТЬ ОПРЕДЕЛЕНИЯ И
ПРИМЕРЫ ПОСТРОЕНИЯ ГРАФИКОВ
Найти интересные формы графиков уравнений с
двумя переменными.Выполнить №396, 399, 404.
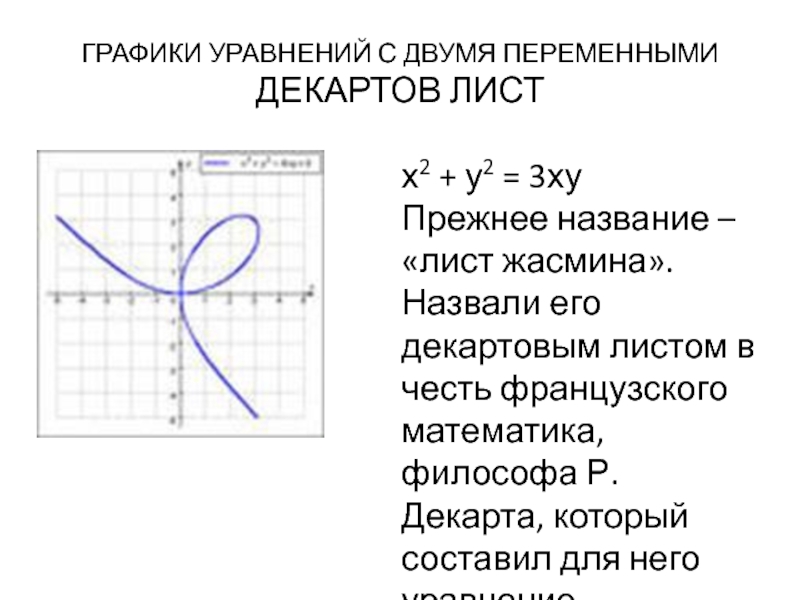
Слайд 13ГРАФИКИ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ
ДЕКАРТОВ ЛИСТ
х2 + у2 = 3ху
Прежнее
название – «лист жасмина». Назвали его декартовым листом в честь
французского математика, философа Р.Декарта, который составил для него уравнение.
Слайд 14
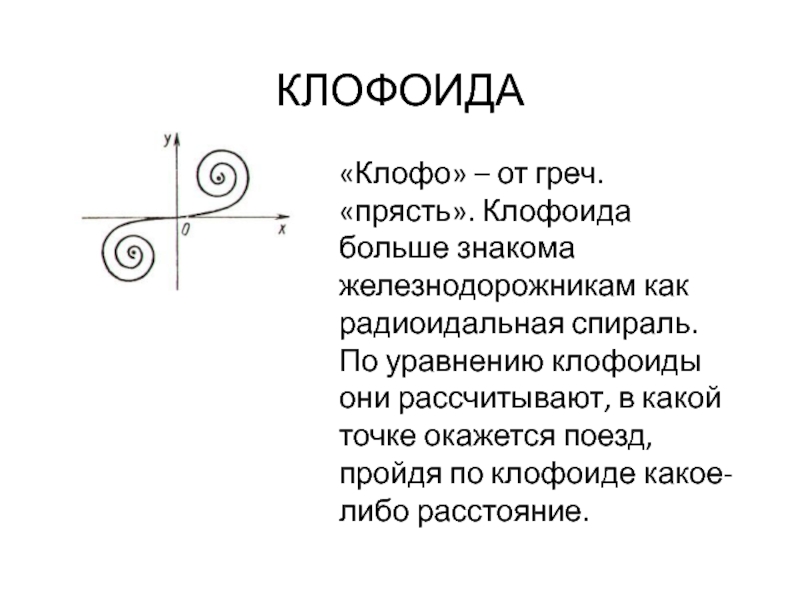
КЛОФОИДА
«Клофо» – от греч. «прясть». Клофоида больше знакома железнодорожникам как
радиоидальная спираль. По уравнению клофоиды они рассчитывают, в какой точке
окажется поезд, пройдя по клофоиде какое-либо расстояние.
Слайд 16СТАТИСТИЧЕСКИЙ ОТЧЁТ
4,5 - 5 баллов - оценка «5», отлично,
так держать.
3,5 - 4,4 балла - оценка «4», хорошо,
но пока не отлично.2,8 - 3,4 балла - оценка «3», базовый уровень достигнут, а могу ли я лучше?
Если ваш результат пока не достиг 2,8 баллов, не отчаивайтесь.
Слайд 17ЖЕЛАЮ УДАЧИ
ДО СКОРОЙ ВСТРЕЧИ
ПРИ ИЗУЧЕНИИ ТЕМЫ
«ГРАФИЧЕСКИЙ СПОСОБ
РЕШЕНИЯ
СИСТЕМ УРАВНЕНИЙ»
